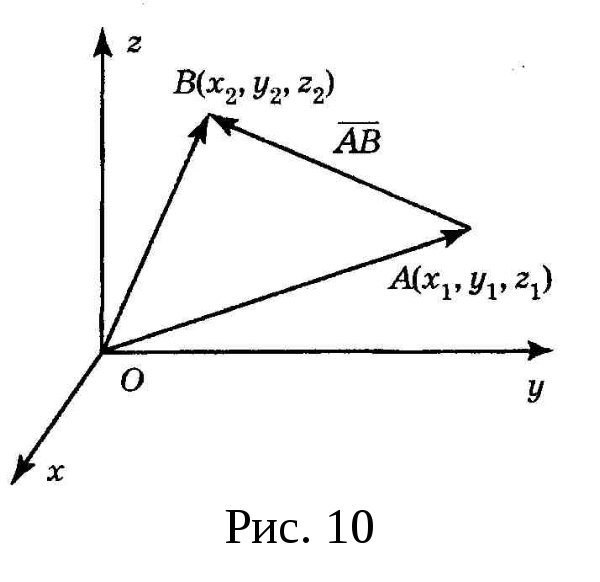
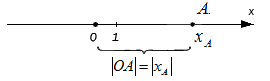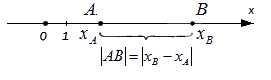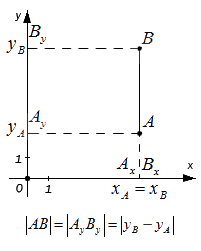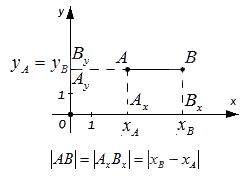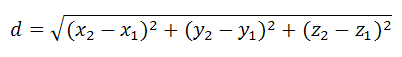Расстояние d между точками в пространстве A11;y1;z1>, A22;y2;z2> представляется формулой
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.3 / 5. Количество оценок: 8
Оценок пока нет. Поставьте оценку первым.
3 комментария
найти расстояние между точками с(-2;1;-2) д (-1;2;1) м (-1;0;2) н (1;-1;2) найти 3 вектора сд — 2 вектора мн
Расстояние от точки до точки: формулы, примеры, решения
В данной статье рассмотрим способы определить расстояние от точки до точки теоретически и на примере конкретных задач. И для начала введем некоторые определения.
Расстояние между точками – это длина отрезка, их соединяющего, в имеющемся масштабе. Задать масштаб необходимо, чтобы иметь для измерения единицу длины. Потому в основном задача нахождения расстояния между точками решается при использовании их координат на координатной прямой, в координатной плоскости или трехмерном пространстве.
Расстояние между точками на координатной прямой
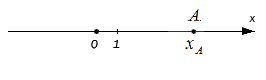
Исходные данные: координатная прямая O x и лежащая на ней произвольная точка А . Любой точке прямой присуще одно действительное число: пусть для точки А это будет некое число х A , оно же – координата точки А .
В целом можно говорить о том, что оценка длины некого отрезка происходит в сравнении с отрезком, принятым за единицу длины в заданном масштабе.
Если точке А соответствует целое действительное число, отложив последовательно от точки О до точки по прямой О А отрезки – единицы длины, мы можем определить длину отрезка O A по итоговому количеству отложенных единичных отрезков.
К примеру, точке А соответствует число 3 – чтобы попасть в нее из точки О , необходимо будет отложить три единичных отрезка. Если точка А имеет координату – 4 – единичные отрезки откладываются аналогичным образом, но в другом, отрицательном направлении. Таким образом в первом случае, расстояние О А равно 3 ; во втором случае О А = 4 .
Если точка A имеет в качестве координаты рациональное число, то от начала отсчета (точка О ) мы откладываем целое число единичных отрезков, а затем его необходимую часть. Но геометрически не всегда возможно произвести измерение. К примеру, затруднительным представляется отложить на координатной прямой дробь 4 111 .
Вышеуказанным способом отложить на прямой иррациональное число и вовсе невозможно. К примеру, когда координата точки А равна 11 . В таком случае возможно обратиться к абстракции: если заданная координата точки А больше нуля, то O A = x A (число принимается за расстояние); если координата меньше нуля, то O A = – x A . В общем, эти утверждения справедливы для любого действительного числа x A .
Резюмируя: расстояние от начала отсчета до точки, которой соответствует действительное число на координатной прямой, равно:
- 0, если точка совпадает с началом координат;
- x A , если x A > 0 ;
- – x A , если x A 0 .
При этом очевидно, что сама длина отрезка не может быть отрицательной, поэтому, используя знак модуля, запишем расстояние от точки O до точки A с координатой x A : O A = x A
Верным будет утверждение: расстояние от одной точки до другой будет равно модулю разности координат. Т.е. для точек A и B , лежащих на одной координатной прямой при любом их расположении и имеющих соответственно координаты x A и x B : A B = x B – x A .
Расстояние между точками на плоскости
Исходные данные: точки A и B , лежащие на плоскости в прямоугольной системе координат O x y с заданными координатами: A ( x A , y A ) и B ( x B , y B ) .
Проведем через точки А и B перпендикуляры к осям координат O x и O y и получим в результате точки проекции: A x , A y , B x , B y . Исходя из расположения точек А и B далее возможны следующие варианты:
– если точки А и В совпадают, то расстояние между ними равно нулю;
– если точки А и В лежат на прямой, перпендикулярной оси O x (оси абсцисс), то точки и совпадают, а | А В | = | А y B y | . Поскольку, расстояние между точками равно модулю разности их координат, то A y B y = y B – y A , а, следовательно A B = A y B y = y B – y A .
– если точки A и B лежат на прямой, перпендикулярной оси O y (оси ординат) – по аналогии с предыдущим пунктом: A B = A x B x = x B – x A
– если точки A и B не лежат на прямой, перпендикулярной одной из координатных осей, найдем расстояние между ними, выведя формулу расчета:
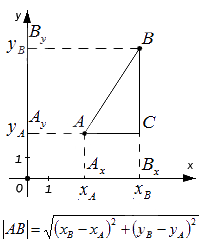
Мы видим, что треугольник А В С является прямоугольным по построению. При этом A C = A x B x и B C = A y B y . Используя теорему Пифагора, составим равенство: A B 2 = A C 2 + B C 2 ⇔ A B 2 = A x B x 2 + A y B y 2 , а затем преобразуем его: A B = A x B x 2 + A y B y 2 = x B – x A 2 + y B – y A 2 = ( x B – x A ) 2 + ( y B – y A ) 2
Сформируем вывод из полученного результата: расстояние от точки А до точки В на плоскости определяется расчётом по формуле с использованием координат этих точек
A B = ( x B – x A ) 2 + ( y B – y A ) 2
Полученная формула также подтверждает ранее сформированные утверждения для случаев совпадения точек или ситуаций, когда точки лежат на прямых, перпендикулярных осям. Так, для случая совпадения точек A и B будет верно равенство: A B = ( x B – x A ) 2 + ( y B – y A ) 2 = 0 2 + 0 2 = 0
Для ситуации, когда точки A и B лежат на прямой, перпендикулярной оси абсцисс:
A B = ( x B – x A ) 2 + ( y B – y A ) 2 = 0 2 + ( y B – y A ) 2 = y B – y A
Для случая, когда точки A и B лежат на прямой, перпендикулярной оси ординат:
A B = ( x B – x A ) 2 + ( y B – y A ) 2 = ( x B – x A ) 2 + 0 2 = x B – x A
Расстояние между точками в пространстве
Исходные данные: прямоугольная система координат O x y z с лежащими на ней произвольными точками с заданными координатами A ( x A , y A , z A ) и B ( x B , y B , z B ) . Необходимо определить расстояние между этими точками.
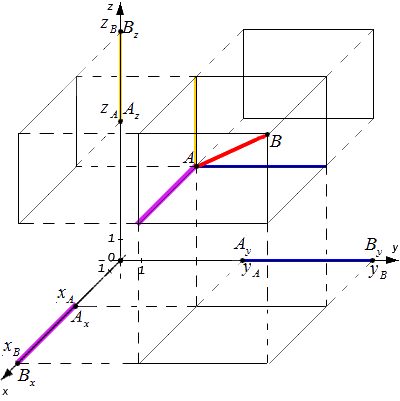
Рассмотрим общий случай, когда точки A и B не лежат в плоскости, параллельной одной из координатных плоскостей. Проведем через точки A и B плоскости, перпендикулярные координатным осям, и получим соответствующие точки проекций: A x , A y , A z , B x , B y , B z
Расстояние между точками A и B являет собой диагональ полученного в результате построения параллелепипеда. Согласно построению измерения этого параллелепипеда: A x B x , A y B y и A z B z
Из курса геометрии известно, что квадрат диагонали параллелепипеда равен сумме квадратов его измерений. Исходя из этого утверждения получим равенство: A B 2 = A x B x 2 + A y B y 2 + A z B z 2
Используя полученные ранее выводы, запишем следующее:
A x B x = x B – x A , A y B y = y B – y A , A z B z = z B – z A
A B 2 = A x B x 2 + A y B y 2 + A z B z 2 = x B – x A 2 + y B – y A 2 + z B – z A 2 = = ( x B – x A ) 2 + ( y B – y A ) 2 + z B – z A 2
Итоговая формула для определения расстояния между точками в пространстве будет выглядеть следующим образом:
A B = x B – x A 2 + y B – y A 2 + ( z B – z A ) 2
Полученная формула действительна также для случаев, когда:
– лежат на одной координатной оси или прямой, параллельной одной из координатных осей.
Примеры решения задач на нахождение расстояния между точками
Исходные данные: задана координатная прямая и точки, лежащие на ней с заданными координатами A ( 1 – 2 ) и B ( 11 + 2 ) . Необходимо найти расстояние от точки начала отсчета O до точки A и между точками A и B .
Решение
- Расстояние от точки начала отсчета до точки равно модулю координаты этой точки, соответственно O A = 1 – 2 = 2 – 1
- Расстояние между точками A и B определим как модуль разности координат этих точек: A B = 11 + 2 – ( 1 – 2 ) = 10 + 2 2
Ответ: O A = 2 – 1 , A B = 10 + 2 2
Исходные данные: задана прямоугольная система координат и две точки, лежащие на ней A ( 1 , – 1 ) и B ( λ + 1 , 3 ) . λ – некоторое действительное число. Необходимо найти все значения этого числа, при которых расстояние А В будет равно 5 .
Решение
Чтобы найти расстояние между точками A и B , необходимо использовать формулу A B = ( x B – x A ) 2 + y B – y A 2
Подставив реальные значения координат, получим: A B = ( λ + 1 – 1 ) 2 + ( 3 – ( – 1 ) ) 2 = λ 2 + 16
А также используем имеющееся условие, что А В = 5 и тогда будет верным равенство:
λ 2 + 16 = 5 λ 2 + 16 = 25 λ = ± 3
Ответ: А В = 5 , если λ = ± 3 .
Исходные данные: задано трехмерное пространство в прямоугольной системе координат O x y z и лежащие в нем точки A ( 1 , 2 , 3 ) и B – 7 , – 2 , 4 .
Решение
Для решения задачи используем формулу A B = x B – x A 2 + y B – y A 2 + ( z B – z A ) 2
Подставив реальные значения, получим: A B = ( – 7 – 1 ) 2 + ( – 2 – 2 ) 2 + ( 4 – 3 ) 2 = 81 = 9
Векторы в пространстве и метод координат
Существует два способа решения задач по стереометрии
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
Система координат в пространстве
Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.
Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами и :
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.
Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму:
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.
Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов и , а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
То есть A + C + D = 0.
Аналогично для точки K:
Получили систему из трех уравнений:
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
Выразим C и B через A и подставим в третье уравнение:
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.
Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂
Строим чертеж. Прямую четырехугольную призму можно по-другому назвать “параллелепипед”.
Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор .
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Получим:
Ответ:
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.
Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.
Находим синус угла между прямой m и плоскостью α по формуле:
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат
Находим координаты вектора .
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Ответ:
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA1 = . Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:
Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему. Выберем
Тогда
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/matematika/vektory/rasstojanie-mezhdu-tochkami/
http://ege-study.ru/ru/ege/materialy/matematika/vektory-v-prostranstve-i-metod-koordinat/
[/spoiler]
Skip to content
Длина вектора в пространстве
Длиной (или модулем) вектора называется расстояние между началом и концом вектора.
Длина вектора a{X,Y,Z} выражается через его координаты следующей формулой:
Пример
Длина вектора $aleft{ { — 2,3,sqrt 3 } right}$ равна
$left| a right| = sqrt {{X^2} + {Y^2} + {Z^2}} = $
$sqrt {{{left( { — 2} right)}^2} + {3^2} + {{left( {sqrt 3 } right)}^2}} = sqrt {16} = 4$
Расстояние между двумя точками в пространстве
Расстояние d между точками в пространстве A1{x1;y1;z1}, A2{x2;y2;z2} представляется формулой
Пример
Расстояние между точками A1{4;-6;3} и A2 {-1;5;-4}
$d = sqrt {{{left( {{x_2} — {x_1}} right)}^2} + {{left( {{y_2} — {y_1}} right)}^2} + {{left( {{z_2} — {z_1}} right)}^2}} = $
$=sqrt {{{left( { — 1 — 4} right)}^2} + {{left( {5 — left( { — 6} right)} right)}^2} + {{left( { — 4 — 3} right)}^2}} =$
$ =sqrt {25 + 121 + 49} = sqrt {195} approx 14$
12648
Пусть векторы
и
заданы своими проекциями:
=(
,
,
),
Разложим векторы по формуле (6):
Эти соотношения почленно сложим и
учтём, что по свойству умножения вектора
на число
.
Получим
или
+
=(
+
;
+
;
+
). (7)
Аналогично для
разности
–
=(
–
;
–
;
–
).
(8)
Точно так же для
произведения
и
=(
,
,
). (9)
Формула (7)
показывает, что проекция на ось координат
суммы векторов равна сумме проекций
на эту ось слагаемых векторов. Подобное
утверждение имеет место для формулы
(8). Формула (9) показывает, что при
умножении вектора на число
на это число умножаются все проекции
вектора.
§7. Длина вектора. Расстояние между двумя точками
Пусть вектор
задан своими проекциями:
=(
,
,
).
Перенесём его параллельно себе так,
чтобы его начало совпало с началом
координат. Получим
=
.
Из рис. 9 видно, что
.
Согласно (5)
аналогично
и
.
Эти числа подставим в предыдущую формулу
и получим
.
Извлечём квадратный корень и найдем
длину вектора:
. (10)
З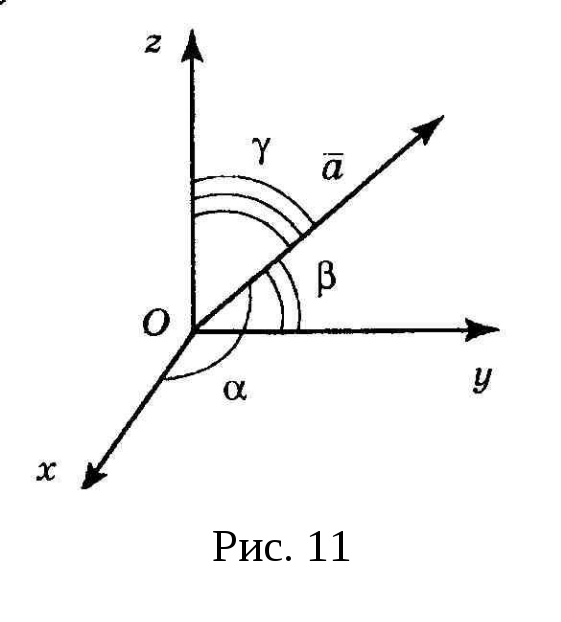
Пусть в пространстве Oxyz
точки
и
заданы координатами А
и В
(рис. 10). Нужно найти расстояние между
ними.
Так как координаты
точки
равны
проекциям на оси координат радиус-вектора
этой точки, то
и
=
.
Согласно (8)
=
,
но
Значит,
Отсюда видно, что проекции на оси
координат вектора равны разностям
соответствующих координат его конца
и начала. Зная проекции
,
по формуле (10) найдём длину вектора
,
следовательно, и расстояние между
точками
и
||=
§8. Направляющие косинусы вектора
Пусть в пространстве
Oxyz
задан
вектор
=(
,
,
).
Поместим его начало в начало координат.
Пусть
– углы, образованные вектором
с осями координат Ox,
Oy,
Oz
(рис. 11).
По формуле (3) для проекций этого вектора
на оси координат имеем
(11)
В правые части
вместо ||
подставим (10) и выразим косинусы углов:
(12)
Они называются
направляющими
косинусами вектора
.
Если все равенства в (12) возведём в
квадрат и почленно сложим, то получим
.
Для единичного вектора, у которого
||=1,
формулы (11) примут вид
.
Отсюда
§9. Скалярное произведение векторов, угол между
векторами. Условие ортогональности
двух векторов
Даны два вектора
и
,
начала которых расположены в одной
точке, а угол между векторами равен
.
Такое расположение мы всегда можем
получить, перенеся один из векторов
параллельно.
Скалярное
произведение двух векторов
и
обозначается
(либо
)
и определяется как число, равное
произведению длин этих векторов на
косинус угла между ними, т. е.
(,
)=|
||
|
. (13)
Из определения
ясно, что ||
=
(проекция
на
).
С учётом этого соотношения формулу
(13) запишем так:
(,
)
= ||
или (,
)
= ||
.
(14)
Скалярное
произведение двух векторов равно
произведению длины одного вектора и
проекции другого вектора на направление
первого. Угол
между векторами
и
будем обозначать также
.
Скалярное
произведение обладает следующими
свойствами:
Первое
свойство показывает, что сомножители
можно поменять местами; второе – что
постоянный скалярный множитель можно
вынести за знак скалярного произведения;
третье – что при скалярном умножении
векторов можно использовать правило
умножения многочленов. Первые два
свойства проверяются на основании
определения скалярного произведения
векторов, т. е. с помощью формулы
(13). Докажем третье свойство.
С учётом (14) запишем
(,
+
)=|
|
=|
|
+|
|
=(
,
)+(
,
).
Пусть векторы
заданы своими проекциями:
поэтому
=
+
+
,
=
+
+
.
Сначала для произведений базисных
векторов
,
докажем справедливость соотношений
(,
)=1;
(,
)=1; (
,
)=1; (15)
(,
)=0;
(,
)=0; (
,
)=0; (16)
Действительно,
по формуле (13) имеем ()=|
||
|
,
поэтому (,
)=1.
Далее, (,
)=|
||
|
=0.
Остальные равенства в (15) и (16) доказываются
аналогично.
Запишем скалярное
произведение
(,
)=(
+
+
,
+
+
).
Использовав второе
и третье свойства скалярного произведения,
будем иметь
(,
)=
(
,
)+
(
,
)+
(
,
)+
(
,
)+
+(
,
)+
(
,
)+
(
,
)+(
Отсюда с учётом
(15) и (16) получим
(,
)=
+
+
. (17)
Таким образом,
скалярное произведение векторов равно
сумме произведений одноименных проекций
этих векторов.
Вычисление угла
между векторами.
Запишем ||
и ||
через проекции с использованием формулы
(10). Из (13) следует, что
.
Следовательно, согласно (17)
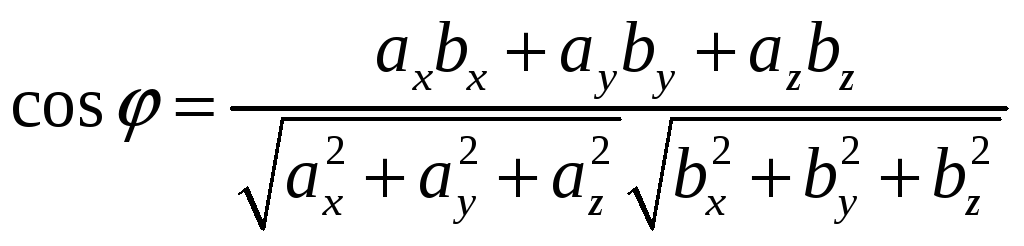
Зная
найдем угол
Условие
ортогональности (перпендикулярности)
двух векторов. Если
для ненулевых векторов
и
их скалярное произведение (,
)=0,
то вектор
ортогонален вектору
В самом деле, пусть
(,
)=0,
тогда согласно (13) имеем (,
)=|
||
|
=0.
Так как
,
,
то
=0.
Значит,
,
т. е. векторы ортогональны.
Условие
ортогональности двух векторов с учётом
(17) можно записать следующим образом:
+
+
=0.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Длина направленного отрезка определяет числовое значение вектора и называется длиной, или модулем, вектора.
Из теоремы Пифагора следует, что в треугольнике (ABC) длина отрезка (AB), которая является модулем вектора
AB→
, равна
AC2+CB2
, и, следовательно, модуль (длина) вектора
AB→
рассчитывается по формуле
AB→=x2+y2
.
Пример:
вычисли длину вектора
AB→=5;3
.
Расстояние между двумя точками
Как известно, координаты вектора можно определить, если даны координаты начальной и конечной точек вектора
Ax1;y1
и
Bx2;y2
.
Если
x=x2−x1
,
y=y2−y1
и
AB→=x2+y2
, то вместо (x) и (y) можно поставить их выражения.
Новую формулу называют не только формулой длины вектора, но и формулой расстояния между двумя точками с заданными координатамиAB=x2−x12+y2−y12.
Так как выражения в скобках в квадрате, то справедливо, что
.
То есть, не важна последовательность координат в разности.
Обрати внимание!
Если даны координаты начальной и конечной точек вектора
Ax1;y1
и
Bx2;y2
, то
AB→x2−x1;y2−y1
.
Обязательно из координат конечной точки надо вычитать координаты начальной точки!
Но при определении длины вектора в формуле последовательность координат не имеет значения:
AB→=x2−x12+y2−y12=x1−x22+y1−y22
.
План урока:
Прямоугольная система координат
Координаты вектора
Координаты середины отрезка
Вычисление длины векторов и расстояния между точками
Коллинеарность векторов
Определение компланарности векторов
Скалярное произведение векторов
Прямоугольная система координат
В планиметрии мы уже рассматривали прямоугольную систему координат. Ее образовывали 2 перпендикулярные друг другу оси – Ох и Оу. С ее помощью можно было определить положение любой точки на координатной плоскости, просто указав две ее координаты – абсциссу х и ординату у.
В стереометрии необходимо определять положение точки уже не на плоскости, а в пространстве. Для этого добавляется третья ось Оz, которую ещё называют осью апликат. Каждые пара осей образует свою отдельную координатную плоскость, всего получается три таких плос-ти: Оху, Охz и Oуz.
Точка О именуется началом координат. Она делит каждую ось на два луча, один из которых – это положительная полуось, а второй – отрицательная полуось.
Для каждой точки в пространстве можно указать три координаты, однозначно определяющие ее положение в пространстве. Пусть в пространстве есть некоторая точка М. Опустим из нее перпендикуляры на координатные плоскости. В свою очередь из этих проекций точки М опустим перпендикуляры уже на координатные оси. В результате будет построен прямоугольный параллелепипед. Измерения этого параллелепипеда и будут координатами точки М:
Если точка M находится в одной из координатных плоскостей, то одна из ее координат будет нулевой. Например, если М принадлежит плоскости Охz, то нулю будет равна координата у. Если же точка располагается на одной из координатных осей, то у нее уже две координаты будут нулевыми. Так, если точка находится на оси Ох, то только координата х может быть ненулевой, а у и z окажутся нулевыми координатами.
На показанном рисунке ребра параллелепипеда лежат на положительных полуосях, поэтому все координаты положительны. Если же какие-то ребра будут лежать на отрицательных полуосях, то и соответствующие координаты будут отрицательными.
Координаты вектора
Введем в пространстве прямоугольную систему коорд-т, а далее от ее начала отложим вектора i, j и k, которые соответственно будут лежать на координатных осях Ох, Оу и Оz, и длина которых составит единицу. Эти вектора именуют координатными векторами, единичными векторами или просто ортами.
Ясно, что орты находятся в разных плоскостях, то есть они образуют тройку некомпланарных векторов. Это означает, что любой вектор а в пространстве можно разложить на орты:
где х, у и z – какие-то действительные числа. Они как раз и считаются координатами вектора а. Записываются коорд-ты вектора в фигурных скобках. На следующем рисунке показан вектор а{3; – 2; – 4}.
Задание. Разложите на орты вектор
Если начало вектора ОМ располагается в начале системы координат О, то вектор ОМ именуют радиус-вектором. В таком случае коорд-ты точки конца вектора, то есть точки М, совпадают с коорд-тами самого вектора ОМ.
Это свойство радиус-вектора мы уже изучали в 9 классе в планиметрии, и в стереометрии оно сохраняется.
Задание. О – начало координат, а точка М имеет коорд-ты (2; 5; – 3). Найдите коорд-ты вектора ОМ.
Решение. Всё очень просто – коорд-ты вектора будут совпадать с коорд-тами его конца, так его начало совпадает с началом коорд-т:
Также в стереометрии остаются справедливыми ещё несколько правил, которые были доказаны в курсе планиметрии:
Задание. Найдите сначала сумму, а потом разность векторов а{3; 7; 5} и b{2; 4; 6}.
Решение. Будем обозначать коорд-ты векторов через индексы. Например, коорд-ты вектора а – это ха, уа и zа. Пусть сумма векторов будет вектором с, а их разность – вектором d. Для вычисления суммы надо складывать соответствующие координаты:
Для вычисления разности надо из коорд-т вектора а вычитать коорд-ты вектора b:
Задание. Вычислите коорд-ты вектора р, зная, что:
Решение. Для вычисления координат надо в выражении для вектора р сами векторы заменить на их координаты:
Получается, что вектор p имеет координаты {0; – 2; 3}.
Теперь мы можем доказать ещё одно утверждение, уже известное из курса планиметрии:
Действительно, пусть есть некоторый вектор АВ, причем коорд-ты точек А и В известны. Построим радиус-вектора OА и OВ:
Координаты радиус-векторов будут совпадать с координатами их концов:
ч. т. д.
Задание. Определите коорд-ты вектора CD, если даны коорд-ты точек С и D: С(3; 8; – 5) и D(5; 4; 1).
Решение. Здесь надо просто из коорд-т точки D, являющейся концом вектора, вычесть коорд-ты точки С:
Задание. От точки K(10; 6; 13) отложен вектор m{3; 2; 5}, конец совпал в точку H. Найдите коорд-ты точки H.
Решение. Коорд-ты вектора m и его концов связаны формулами:
Координаты середины отрезка
Пусть в пространстве есть отрезок АВ, и координаты его концов известны. Точка М – середина этого отрезка. Как вычислить ее координаты? Рассмотрим взаимосвязь векторов АМ, МВ и АВ:
Раз М – середина АВ, то вектора АМ и МВ имеют равные длины, и при этом они находятся на одной прямой. Значит, эти вектора равны и потому у них одинаковые коорд-ты:
Аналогично можно получить аналогичные формулы для коорд-т у и z:
Рассмотрим несколько задач на координаты точек.
Задание. Найдите коорд-ты середины отрезка, соединяющего точки А(3; 7; 12) и В(1; 5; – 4).
Решение. Просто используем только что выведенные формулы. Середину также обозначаем буквой М:
Задание. Известно, что K середина отрезка CD. Даны координаты точек С и K: С(12; 9; – 3) и K(15; 7; 3). Найдите коорд-ты D.
Решение. Сначала запишем формулу для коорд-ты х:
Вычисление длины векторов и расстояния между точками
Рассмотрим радиус-вектор ОМ с коорд-тами {x; у; z}. Попытаемся найти его длину. Мы можем построить прямоугольный параллелепипед, в котором этот вектор окажется диагональю:
Напомним, что квадрат длины диагонали в прямоугольном параллелепипеде равен сумме квадратов его измерений. Но в полученном параллелепипеде измерения – это коорд-ты х, у и z, поэтому можно записать:
Так как равные вектора имеют как одинаковы и коорд-ты, и длина, то ясно, что каждый вектор с коорд-тами {x; y; z} будет равен рассмотренному радиус-вектору, а значит и его длина будет рассчитываться по такой же формуле.
Задание. Найдите длину вектора m{– 2; 9; 6}.
Решение. Просто используем формулу:
Рассмотрим отрезок АВ с известными коорд-тами его концов. Можно построить вектор АВ, его коорд-ты будут определяться так:
Задание. Найдите расстояние между точкой K(10; 15; 5) и M(16; 21; – 2).
Решение. Просто подставляем коорд-ты точек в формулу:
Задание. Найдите длину медианы KM в ∆ KPN, если известны коорд-ты его вершин: P(2; 5; 8), N (6; 9; 12) и K(16; 11; 13).
Решение. Для нахождения длины медианы достаточно знать коорд-ты ее концов. Коорд-ты K уже известны, а M – середина PN, что позволяет вычислить и ее коорд-ты:
Коллинеарность векторов
Напомним, что если два вектора а и b коллинеарны друг другу, то должно существовать такое число k, что
Полученное отношение (1) является одновременно и признаком коллинеарных векторов, и их свойством. Слово «признак» означает, что любые вектора, чьи координаты соответствуют условию (1), будут коллинеарны. Слово «свойство» означает обратное – если известно, что вектора коллинеарны, то для них обязательно выполняется условие (1). В таких случаях в математике может использоваться словосочетание «тогда и только тогда»:
Очень важно то, что это правило действует только в случае, если все коорд-ты векторов ненулевые. Теперь рассмотрим случай, когда какие-то коорд-ты вектора b (одна или две из них) равны нулю. Например, пусть
В результате мы выяснили, что если коорд-та одного вектора нулевая, то и у любого вектора, коллинеарному ему, эта же коорд-та также должна быть нулевой. Особняком стоит случай с нулевым вектором с коорд-тами {0; 0; 0}. Он условно признается коллинеарным любому вектору.
Задание. Выясните, какие из этих пар векторов коллинеарны:
Решение. В первом задании просто делим друг на друга соответствующие коорд-ты и находим значение коэффициента k:
Значение коэффициента k оказалось одинаковым для каждой пары коорд-т, значит, вектора коллинеарны.
Повторяем эти действия в задании б):
На этот раз коэффициенты k оказались различными, значит, вектора неколлинеарны.
В задании в) у вектора е коорд-та z нулевая. Значит, если и у вектора f, если он коллинеарен z, эта координата должна быть нулевой, но это не так. Значит, вектора e и f неколлинеарны.
В задании г) снова указаны вектора с нулевыми коорд-тами. Но у обоих векторов коорд-та z нулевая, поэтому они могут быть коллинеарными. Однако необходимо проверить, что отношение ненулевых координат одинаково:
Коэффициент k получился одинаковым, поэтому вектора коллинеарны.
В последнем задании д) вектор n – нулевой, ведь все его коорд-ты нулевые. Нулевой вектор всегда коллинеарен другим векторам, в том числе и в этом задании.
Ответ: а) да; б) нет; в) нет; г) да; д) да.
Задание. Выясните, располагаются ли на одной прямой точки А(3; 5; 12), В(5; 7; 16) и С(0; 2; 6).
Решение. Ясно, что если эти точки находятся на одной прямой, то вектора АВ и ВС будут коллинеарными. Если же эти вектора неколлинеарны, то и точки должны находиться на разных прямых.
Сначала вычислим коорд-ты векторов АВ и ВС:
Теперь проверяем, коллинеарны ли эти вектора:
Коэффициенты k одинаковы, а потому АВ и ВС – коллинеарные векторы. Значит, точки А, В и С находятся на одной прямой.
Определение компланарности векторов
Пусть у нас есть три вектора с известными коорд-тами:
Как определить, компланарны ли эти вектора, то есть располагаются ли они в одной плоскости? Если эти вектора компланарны, то, по признаку компаланарности, вектор а можно разложить на вектора b и с:
где х и y – некоторые числа. Но если такое разложение существует, то коорд-ты векторов а, b и с будут связаны равенствами:
Получили систему из 3 уравнений с двумя неизвестными (х и y). Если такая система имеет решение, то вектора компланарны. Если же решения нет, то вектора не компланарны.
Задание. Определите, компланарны ли вектора
Имеем систему с тремя уравнениями. Из последних двух уравнений очевидно, что его решением может быть только пара чисел:
Значит, рассмотренная тройка векторов компланарна.
Задание. Располагаются ли в одной плос-ти вектора:
Решение. Нам надо проверить компаланарность векторов, поэтому действуем также, как и в предыдущей задаче. Если вектора компланарны, то существует разложение:
Получилось неверное равенство. Это означает, что у системы уравнений решения нет, и потому тройка векторов некомпланарна.
Скалярное произведение векторов
В 9 классе мы уже изучали скалярное произведение векторов.
Для нахождения угла между векторами необходимо отложить их от одной точки, тогда они образуют такой угол.
Задание. Угол между векторами с и d составляет 60°, а их длины соответственно равны 5 и 6. Найдите их скалярное произведение.
Решение. Здесь для расчета просто перемножаем длины векторов и косинус 60°:
Напомним несколько уже известных нам фактов о скалярном произведении, остающихся верными и в стереометрии:
Формула для расчета скалярного произведения по коорд-там векторов, используемая в стереометрии, несколько отличается от формулы из курса планиметрии. Напомним, что в планиметрии произведение векторов а{xа; уа} и b{хb; yb} можно было рассчитать так:
Задание. Вычислите скалярное произведение векторов:
На практике скалярное произведение обычно используется для расчета углов между векторами, а также отрезками и прямыми. Рассмотрим несколько задач.
Задание. Вычислите угол между векторами:
Теперь через скалярное произведение возможно рассчитать косинус искомого нами угла, а затем и сам угол, который мы обозначим как α:
Задание. Рассчитайте углы в ∆АВС, зная коорд-ты его вершин: А(1; – 1; 3), В(3; – 1; 1) и С(– 1; 1; 3).
Решение. Чтобы найти ∠В, необходимо просто рассчитать угол между векторами ВС и ВА также, как это сделано в предыдущей задаче. Но сначала найдем коорд-ты векторов ВС и ВА и их длины:
Далее рассчитываем скалярное произведение векторов:
Теперь найдем угол А, который представляет собой угол между векторам AВ и AС. Вектор AВ – это вектор, противоположный ВA, то у него та же длина, но противоположный знак у коорд-т:
Задание. В прямоугольном параллелепипеде АВСDA1B1C1D1 ребра имеют длину:
AB = 1
BC = 2
BB1 = 2
Рассчитайте угол между векторами DB1 и BC1.
Решение. Введем систему коорд-т Охуz и расположим в нем параллелепипед следующим образом:
При этом построении граничные точки векторов будут иметь следующие коорд-ты:
Находим коорд-ты векторов, а также их длины:
Рассчитываем скалярное произведение DB1 и BC1:
Получили ноль. Из этого вытекает, что вектора перпендикулярны, то есть искомый нами угол составляет 90°.
Ответ: 90°
Сегодня мы научились использовать координаты для решения стереометрических задач. Почти все формулы, используемые в методе координаты, аналогичны тем формулам, которые были выведены ещё в курсе планиметрии. Надо лишь учитывать существование ещё одной, третьей координаты z.