Как найти расстояние между двумя точками?

Расстоянием между точками также называют прямую,
у которой одна из точек это начало, а соответственно
другая конец. Найти расстояние между этими
двумя точками, значит найти длину прямой,
связывающей точки.
Есть много разных способов найти расстояние между
двумя точками, но самый универсальный, на мой взгляд,
это найти расстояние взяв за основу Теорему Пифагора.
Исходя из этой теоремы, можно сказать, что в нашем
случае расстоянием(прямой), является гипотенуза,
а чем тогда являются точки, сейчас разберемся.
Формулировка великой Теоремы Пифагора звучит так:
в прямоугольном треугольнике квадрат гипотенузы равен
сумме квадратов катетов. Или же кратко, формулой:
( c^2 = a^2 + b^2 ) где c — это гипотенуза, a и b — катеты.
Формулировка этой теоремы применяется почти всегда и везде,
где нужно найти расстояние от чего-то до чего-то. Сейчас, мы
используя эту теорему найдем расстояние между точками.
Итак, для примера возьмем точки с координатами
первой точки — x1 = 0; y1 = 4, второй точки — x2 =3; y2 = 0.
Как же нам теперь выразить точки через катеты a и b ?
Читайте дальше, все гениальное просто.
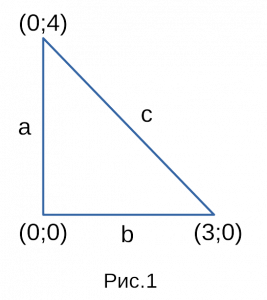
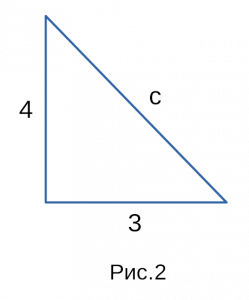
На рисунке 1 мы изобразили для наглядности
прямоугольный треугольник, с координатами
которые мы взяли для примера. На рисунке 2
тот же самый прямоугольный треугольник,
только без координат! Эти два прямоугольных
треугольника идентичные, поэтому вернемся
к Теореме Пифагора.
Заменяем длины катетов a и b, из Теоремы Пифагора,
на разность координат точек. Взгляните на формулу,
которая получилась:
Подставляем наши координаты:
В итоге получилось, что расстояние в нашем примере
равно 5(корень из 25). Как видите все просто, и вы можете
смело применять эту формулу, решая не только задачи,
но и на практике, находя расстояние зная только две точки.
Все формулы для треугольника
1. Как найти неизвестную сторону треугольника
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a , b , c – стороны произвольного треугольника
α , β , γ – противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), ( a ):
* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), ( a):
2. Как узнать сторону прямоугольного треугольника
Есть следующие формулы для определения катета или гипотенузы
a , b – катеты
c – гипотенуза
α , β – острые углы
Формулы для катета, ( a ):
Формулы для катета, ( b ):
Формулы для гипотенузы, ( c ):
Формулы сторон по теореме Пифагора, ( a , b ):
3. Формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы
b – сторона (основание)
a – равные стороны
α – углы при основании
β – угол образованный равными сторонами
Формулы длины стороны (основания), (b ):
Формулы длины равных сторон , (a):
4. Найти длину высоты треугольника
Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.
H – высота треугольника
a – сторона, основание
b, c – стороны
β , γ – углы при основании
p – полупериметр, p=(a+b+c)/2
R – радиус описанной окружности
S – площадь треугольника
Формула длины высоты через стороны, ( H ):
Формула длины высоты через сторону и угол, ( H ):
Формула длины высоты через сторону и площадь, ( H ):
Формула длины высоты через стороны и радиус, ( H ):
Расстояние от точки до прямой
Что называется расстоянием от точки до прямой? Как найти расстояние от точки до прямой?
Расстоянием от точки до прямой называется длина перпендикуляра, опущенного из данной точки на прямую.
Таким образом, чтобы найти расстояние от точки до прямой, надо из точки к прямой провести перпендикуляр и найти его длину.
Например, на рисунке 1 расстояние от точки A до прямой a равно длине перпендикуляра AB, опущенного из точки A на прямую a.
Задачи на нахождение расстояния от точки до прямой сводятся к рассмотрению прямоугольного треугольника.
№ 1. Из точки к прямой проведены две наклонные, длины которых относятся как 2:3, а длины их проекций соответственно равны 2 см и 7 см. Найти расстояние от точки до прямой.
Дано: A∉a,
BC и BD — их проекции, BC=2 см, BD=7 см
1) Пусть k — коэффициент пропорциональности. Тогда AC=2k см, AD=3k см.
2) Рассмотрим треугольник ABC — прямоугольный (так как AB — перпендикуляр к прямой a по условию). По теореме Пифагора
3) Аналогично, из треугольника ABD
4) Приравниваем правые части полученных равенств и находим k:
5) Зная k, найдем AB:
№ 2. Из точки к прямой проведены две наклонные, длины которых равны 13 см и 15 см. Найти расстояние от точки до прямой, если разность проекций наклонных равна 4 см.
Дано: A∉a,
AC и AD — наклонные, AC=13 см, AD=15 см,
BC и BD — их проекции, BD-BC=4 см
1) Пусть BC=x см, тогда BD=x+4 см.
2) Рассмотрим треугольник ABC — прямоугольный (так как AB — перпендикуляр к прямой a по условию). По теореме Пифагора
3) Аналогично, из треугольника ABD
4) Приравниваем правые части полученных равенств и находим x:
5) Зная x, найдем AB:
№ 3. Найти расстояние от точки A до прямой a, если известно, что наклонная AF, длина которой равна c, образует с прямой a угол α.
Дано: A∉a,
Треугольник ABF — прямоугольный (так как AB — перпендикуляр к прямой a по условию). AB — катет, противолежащий углу ACB, AF — гипотенуза.
[spoiler title=”источники:”]
http://www-formula.ru/2011-10-09-11-08-41
[/spoiler]
Калькулятор длин сторон треугольника онлайн умеет вычислять длину сторон 14 способами.
Калькулятор может:
- Найти все стороны треугольника.
- Найти все углы треугольника.
- Найти площадь (S) и периметр (P) треугольника.
- Найти радиус (r) вписанной окружности.
- Найти радиус (R) описанной окружности.
- Найти высоту (h) треугольника.
Просто введите любые имеюшиеся данные и, если их достаточно, то калькулятор сам подберет нужные формулы для вычислений и покажет подробный расчет с выводом формул.
Сторона треугольника (или длина сторон) может быть найдена различными методами.
В большинстве случаев достаточно воспользоваться одной из ниже приведенных формул. Однако не редки случаи когда для нахождения искомой стороны понадобиться обратиться к дополнительным материалам или решения в два действия.
Как найти длину стороны треугольника?
Найти длину сторон треугольника очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.
Для прямоугольного треугольника:
1) Найти катет через гипотенузу и другой катет


где a и b – катеты, с – гипотенуза.
2) Найти гипотенузу по двум катетам


где a и b – катеты, с – гипотенуза.
3) Найти катет по гипотенузе и противолежащему углу


где a и b – катеты, с – гипотенуза,α° и β° – углы напротив катетов.
4) Найти гипотенузу через катет и противолежащий угол


где a и b – катеты, с – гипотенуза,α° и β°- углы напротив катетов.
Для равнобедренного треугольника:
1) Найти основание через боковые стороны и угол между ними


где a – искомое основание, b – известная боковая сторона,α° – угол между боковыми сторонами.
2) Найти основание через боковые стороны и угол при основании


где a – искомое основание,b – известная боковая сторона,β° – угол при осноавнии.
3) Найти боковые стороны по углу между ними


где b – искомая боковая сторона, a – основание,α° – угол между боковыми сторонами.
4) Найти боковые стороны по углу при основании


где b – искомая боковая сторона, a – основание,β° – угол при осноавнии.
Для равностороннего треугольника:
1) Найти сторону через площадь


где a – искомая сторона, S – площадь треугольника.
2) Найти сторону через высоту


где a – искомая сторона,h – высота треугольника.
3) Найти сторону через радиус вписанной окружности


где a – искомая сторона,r – радиус вписанной окружности.
4) Найти сторону через радиус описанной окружности


где a – искомая сторона,R – радиус описанной окружности.
Для произвольного треугольника:
1) Найти сторону через две известные стороны и один угол (теорема косинусов)


где a – искомая сторона, b и с – известные стороны, α° – угол напротив неизвестной стороны.
2) Найти сторону через одну известную сторону и два угла (теорема синусов)


где a – искомая сторона, b – известная сторона, α° и β° известные углы.
Скачать все формулы в формате Word
|
Найдите расстояние (по прямой) между противоположными углами обеденного стола. Ответ дайте в метрах квадратных.
Владелец собирается провести ремонт своей квартиры. На плане изображена предполагаемая расстановка мебели и бытовой техники на кухне после ремонта. Сторона каждой клетки равна 0,3 м. Кухня имеет квадратную форму. Единственная дверь кухни деревянная, в стене напротив двери расположено окно. Справа от двери будут поставлены полки для посуды, слева от двери будет смонтирована раковина для мытья посуды. В углу слева от окна предполагается разместить газовую плиту. Между раковиной и плитой будет собран буфет, отмеченный цифрой 3. Площадь, занятая буфетом, по плану будет равна 0,72 м2. В центре кухни планируется поставить обеденный стол. Кроме того, в угол кухни будет поставлен холодильник, занимающий 0,36 м2 пола. Пол кухни (в том числе там, где будет стоять мебель и бытовая техника) планируется покрыть плиткой размером 30 см × 30 см. Кроме того, владелец квартиры планирует смонтировать на кухне электрический подогрев пола. Чтобы сэкономить, владелец не станет подводить обогрев под холодильник, плиту, буфет, раковину и полки для посуды, а также на участок площадью 0,18 м2 между буфетом и плитой.
Весьма хитрая задача. На плане обозначен прямоугольный стол со сторонами 3 и 4 клеток, а длина измеряется не в квадратных метрах, а просто в метрах. Длина между углами данного стола представляет собой гипотенузу прямоугольного треугольника и равна корню квадратному из суммы квадратов катетов. Так гласит формула теоремы Пифагора. Подставляем значения: √ (3²+ 4²) = √ (9 + 16) = √ (25) = 5. Конечно любой знакомый с математикой не станет это вычислять. Ведь перед ним магический квадрат – 3, 4, 5. Теперь зная размер гипотенузы мы вычислим длину в метрах: 5 * 0.3 = 1.5 метра или 150 сантиметров или 15 дециметров. автор вопроса выбрал этот ответ лучшим
Simple Ein более года назад Из условия задачи понятно, что обеденный стол обозначен цифрой 4. Обеденный стол со сторонами 3 и 4 клетки. Сторона каждой клетки равна 0,3 м. Получается, одна сторона стола равна 0,3*3=0,9 м. Вторая – 0,4*3=1,2 м. Определить расстояние между противоположными углами у стола можно по теореме Пифагора. Получается √ (0,9²+ 1,2²) = √ (2,25) =1,5 метра. Пашенька 12 месяцев назад Пояснение к задаче нам подсказывает, что обеденный стол на схеме расположен в центре кухни, поэтому можем смело утверждать, что нас интересует объект под номером 4. Из условия задания нам известно, что клетка имеет размер – 0.3м. Для подсчета нам необходимо рассчитать размеры стола. В клеточках это 3х4, в метрах:
Далее учитываем, что стол – это прямоугольник, где расстояние между углами – это гипотенуза, а стороны стола – катеты. Следовательно, на основании теоремы Пифагора мы имеем возможность рассчитать длину-гипотенузу. Находим сумму квадратов катетов и извлекаем квадратный корень.
Ответ: 1.5. Stan1711 3 года назад Длина измеряется в метрах.Из плана видно что размеры ободеного стола равны 3 клетки на 4.Стол прямоугльный.Тогда размер диагонали от одного угла до другого будет ровна 5 клеткам (как соотношение в прямоугольном треугольнике – 3:4:5.)Учитывая размер клетки 0,3м. мы получим ответ на вопрос 5*0,3 =1,5м. Знаете ответ? |
Цели урока:
– повторение и обобщение изученного материала;
– корректирование знаний учащихся;
– формирование умений рассуждать, применять полученные знания.
Ход урока
Устная работа по готовому чертежу
Мы знакомы с теоремами и их следствиями, которые устанавливают взаимосвязь между углами и сторонами в треугольнике. Используя эти теоремы, а также данные чертежа, придумайте всевозможные задачи.
Учащиеся, используя данные чертежа (рис. 1), могут предложить следующие задачи.
Найти величину угла А в треугольнике АВС.
Найти внешний угол DAB треугольника АВС.
Найти градусные меры углов АВН и СВН.
Сравнить длины сторон треугольников АВН и ВНС.
Выяснить, является ли отрезок ВН биссектрисой треугольника АВС.
Очень важно, чтобы, формулируя задачу и отвечая на вопрос, поставленный в ней, учащийся ссылался на теорему или следствия и правильно озвучивал их.
После рассмотрения задач, предложенных учащимся, целесообразно еще раз вернуться к формулировкам известных теорем и свойств треугольника. Опрос может проходить как в устной форме, так и в форме математического диктанта. Его содержание может быть таким.
Закончите предложения (1-10).
В треугольнике сумма углов равна…
Внешний угол треугольника равен…
Если один из внешних углов треугольника равен 90 градусов, то…
В треугольнике против большей стороны лежит…
В треугольнике против меньшего угла лежит…
Если в треугольнике два угла равны, то…
Сумма двух сторон треугольника…
Длина гипотенузы в прямоугольном треугольнике…
Во всяком треугольнике против равных сторон лежат…
Катет, лежащий против угла в 30 градусов, равен…
При оценивании результатов диктанта можно использовать следующие критерии отметки:
«3» – 5-6 верных ответов;
«4» – 7-8 верных ответов;
«5» – 9-10 верных ответов.
Решение задач
Найдите углы 1-3 в треугольнике АВС, используя данные рисунка 2.
Ответ. <1 = 115 градусов, <2 = 65 градусов, <3 = 75 градусов.
В равнобедренном треугольнике угол при основании в два раза больше угла, противолежащего основанию, Найдите углы этого треугольника.
Ответ: 36 градусов, 72 градуса, 72 градуса.
На продолжении стороны АВ треугольника АВС за вершину В отмечена точка D, АС = 18 см, В = 5 см (рис. 3). Может ли отрезок AD быть равным 12 см?
Решение. Из неравенства треугольника следует, что АВ > 13 cм (АВ + ВС > AC). Так как отрезок АD > AB, то длина отрезка AD не может равняться 12 см.
Итог урока
На сегодняшнем уроке мы обобщили знания о взаимосвязи между элементами в треугольнике, повторили необходимые теоремы, следствия, разобрали основные приемы решения задач по теме, оценили свой уровень знаний.
Треугольник является базовой фигурой геометрии, встречающейся повсеместно. Расчет всех геометрических фигур и тел основаны на наличии в них тех или иных треугольников, благодаря чему становится возможным применить множество теорем и формул, несвойственных конкретным фигурам по отдельности. Равносторонние треугольники, равнобедренные треугольники и прямоугольные треугольники составляют каркас решения геометрических задач, и обладая множеством дополнительных построений внутри треугольника, они предоставляют огромное количество значений тех или иных длин. Все биссектрисы, медианы, высоты, радиусы окружностей, вписанных или описанных около таких треугольников, можно рассчитать в этом разделе через геометрический калькулятор. Для этого необходимо ввести любые имеющиеся вводные данные, и калькулятор выдаст не только значения всех остальных параметров треугольника, но и объяснит преобразования формул, использованные для этих расчетов.

