ybaspintise
Вопрос по геометрии:
В единичном кубе A…D1 найдите расстояние между вершиной A и: а) вершиной C1; б) ребром CC1; в) гранью BB1C1C.
Пожалуйста, решите подробно, ОБЯЗАТЕЛЬНО С ЧЕРТЕЖОМ.
Если вы не хотите делать чертеж, то, ПОЖАЛУЙСТА, не приступайте к решению.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 1
irnereatar280
Расстояние между точкой и прямой – это длина перпендикуляра, опущенного из данной точки на данную прямую.
Расстояние между точкой и плоскостью – это длина перпендикуляра, опущенного из данной точки на данную плоскость.
Я решил на листочках, которые прикрепил ниже…
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
A cube with vertices $(0,0,0),(0,0,1),(0,1,0),(0,1,1),(1,0,0),(1,0,1),(1,1,0),$ and $(1,1,1)$ has the point $P_{1}$ with vertices $(frac{1}{2},0,frac{1}{4})$ and the point $P_{2}$ with vertices $(0,frac{3}{4},frac{3}{4})$. What is the length of the shortest path between $P_{1}$ and $P_{2}$ such that the path lies on the surface of the cube?
Note: $sqrt{(frac{1}{2}-0)^2+(0-frac{3}{4})^2+(frac{1}{4}-frac{3}{4})^2}=frac{sqrt{17}}{4}approx1.03078$ is the shortest distance between the two points. However, it is not the correct answer since this path does not lie on the surface of the cube.
For the same cube, can we generalize and give an expression to find the length of the shortest path between $P_{1}(x_{1},y_{1},z_{1})$ and $P_{2}(x_{2},y_{2},z_{2})$, where, clearly, $0leq x_{i},y_{i},z_{i}leq1$?
|
Имеются в виду противоположные вершины куба с ребром, равным 1 метру. Куб сплошной, движение (например, мухи или линии фломастера) происходит по его поверхности. Сколькими способами можно решить эту задачу? Математика! Как давно это было… Если я не ошибаюсь, то из каждой вершины к противоположной можно построить 6 кратчайших путей, длина каждого – квадратный корень из 5 в метрах. автор вопроса выбрал этот ответ лучшим Шкапидар 8 лет назад Диагональ плоскости куба в вашем случае по Пифагору-корень квадратный из двух. Диагональ между противоположными вершинами будет равна по Пифагору-корню квадратному из трёх, как гипотенуза треугольника, один из катетов которого-сторона куба, а второй-диагональ любой его плоскости(равная корню квадратному из двух). Знаете ответ? |

В кубе А…D1 с ребром а найдите расстояние между вершиной А1 и: а) ребром СD б) диагональю ВD в) диагональю АС1 . подскажите, как это решить и какие формулы нужны. Заранее спасибо)
Светило науки – 9801 ответ – 46531 помощь
Для решения надо вычертить куб и провести в нем нужные линии. Можно также использовать дополнительные проекции и сечения куба, чтобы искомые линии попадали в сечение без искажения.
Для образца дается пример в приложении.
а) это диагональ бокового ребра А₁Д = √(а² + а²) = а√2.
б) это линия, перпендикулярная диагонали ВД =√(а² + (а/√2)²) = а√3 / √2.
в) это отрезок до пересечения с диагональю АС₁= а / √2.

Ответ:
Рассчитай расстояние вершины куба до диагонали куба, которая не проходит через эту вершину, если ребро куба — 45 см
Объяснение:
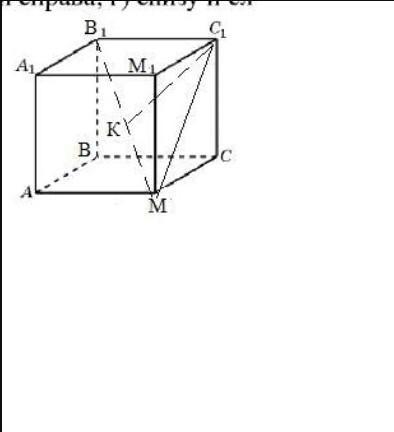
Пусть АВСМА₁В₁С₁М₁-куб, АВ=45см. Все грани равные квадраты.Расстоянием от вершины С₁ до диагонали В₁М будет длина перпендикуляра С₁К.
Найдем диагональ квадрата по т. Пифагора ⇒ 45√2 см.
Найдем диагональ куба d²=45²+45²+45² , d²=3*45² , d=45√3 см.
ΔМВ₁С₁- прямоугольный, т.к. проекция М₁С₁⊥ В₁С₁ , то и наклонная МС₁⊥В₁С₁ по т. о трех перпендикулярах. Используя формулу площади треугольника :
S(В₁С₁М)=1/2*В₁С₁*С₁М или S(В₁С₁М)=1/2*В₁М*С₁К ⇒
S(В₁С₁М)=1/2*45*45√2 , подставим во вторую формулу, получим :
1/2*45*45√2=1/2*45√3*С₁К или С₁К=(45√2)/√3=(45√6)/3=15√6 (см)
Приложения: