1. В графы 13 и 14
ведомости прямых и кривых заносятся
пикетажные обозначения начала и конца
кривых.
2. по заданному
азимуту А1
начального направления трассы и углам
поворота
![]()
(2.18)
или
![]()
где
Ai
-.азимут предыдущего прямого участка
трассы;
Ai+1–
азимут последующего прямого участка
трассы.
В моем
примере А1=69°59′
.
Тогда
А2
=69°59ˈ+44°44’=114°43′;
А3=114°43′-
6°37’=108°06′ и т.д.
Затем
азимуты по известным формулам переводят
в румбы: r1=СВ:
69°59′;
r2
=ЮВ: 65°17′; r3
= ЮВ: 71°54′ и т.д.
Азимуты и румбы
прямых участков трассы заносят в графы
14 и 15.
3. Расстояние между
вершинами углов (графа 12 ведомости)
вычисляют по формуле
![]()
![]()
ВУi
+ Д,
(2.19)
где
ПК ВУi+
1–
пикетажное
обозначение данной вершины угла;
ПК ВУi
– пикетажное обозначение предыдущей
вершины угла;
Дi
– домер,
относящийся, к предыдущей вершине угла.
Длина отрезка от
ПКО до ВУ1′ равна пикетажному обозначению
первой вершины
угла.
В моем
примере:
SПК0,
ВУ1
= 343,45 м
SВУ1,
ВУ2
= (ПК6+56,89)– (ПК3+34,72) + 6,57 = 328,74 м;
SВУ2,
ВУ3 =
(ПК11+39,58) – (ПК6+56,89) + 16,19= 498,88м;
SВУ3,
ПК15 = ПК15 –
(ПК11+39,58) + 3,19 = 363,61м;
34
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
МАОУ СОШ №12 Шкода Л,И, Многогранники

МАОУ СОШ №12
Шкода Л,И,
Многогранники.(Вычисление расстояний между вершинами и углов).
Найдите квадрат расстояния между вершинами

1. Найдите квадрат расстояния между вершинами С и А1 прямоугольного параллелепипеда, для которого АВ = 5 , AD = 4 , AA1 = 3.
Ответ: 50
4
5
3
5
Найдите расстояние между вершинами

2. Найдите расстояние между вершинами А и D1 прямоугольного параллелепипеда, для которого АВ = 5 , AD = 4 , AA1 = 3.
Ответ: 5
5
4
3
4
Найдите угол ABD1 прямоугольного параллелепипеда, для которого

3. Найдите угол ABD1 прямоугольного параллелепипеда, для которого АВ = 5 , AD = 4 , AA1 = 3. Ответ дайте в градусах.
5
4
3
3
5
Ответ: 45
В правильной шестиугольной призме

4. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками A и E1.
1
1
1
120°
1
Ответ: 2
В правильной шестиугольной призме

5. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками B и E.
1
1
1
1
Ответ: 2
В правильной шестиугольной призме

6. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны . Найдите расстояние между точками B и E1.
Ответ: 5
В правильной шестиугольной призме

7. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите а) тангенс угла AD1D.
1
1
2
Ответ: а)2; б) 60
б)Найдите угол DAB. Ответ дайте в градусах.
Найдите расстояние между вершинами

8. а)Найдите расстояние между вершинами A и C2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Ответ: а) 3
б)Найдите квадрат расстояния между вершинами D и C2.
Ответ: б) 5
Найдите расстояние между вершинами

9. Найдите расстояние между вершинами B1 и D2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
1
2
Ответ: 3
Найдите квадрат расстояния между вершинами

10. Найдите квадрат расстояния между вершинами B и D2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
1
1
2
Ответ: 14
Найдите тангенс угла CDC3 многогранника, изображенного на рисунке

11. Найдите тангенс угла CDC3 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
2
2
Ответ: 1
Найдите квадрат расстояния между вершинами

12. Найдите квадрат расстояния между вершинами C и D2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
2
Ответ: 6
Найдите угол D2EA многогранника, изображенного на рисунке

13. Найдите угол D2EA многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
Δ D2EA – равносторонний, значит,
Ответ: 60
Радиус окружности, описанной около основания правильной треугольной пирамиды, равен 3

14. Радиус окружности, описанной около основания правильной треугольной пирамиды, равен 3. боковое ребро равно 5. Найдите высоту пирамиды.
3
5
Ответ: 4
В правильной треугольной пирамиде

15. В правильной треугольной пирамиде SABC N — середина ребра BC , S — вершина. Известно, что AB = 1 , а площадь боковой поверхности равна 3. Найдите длину отрезка NS .
N
1
Ответ: 2
В правильной треугольной пирамиде

16. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке P . Объем пирамиды равен 1, PS = 1 . Найдите площадь треугольника ABC .
1
Ответ: 3
В правильной четырехугольной пирамиде

17. В правильной четырехугольной пирамиде SABCD диагональ основания равна 6, высота равна 4. Найдите боковое ребро пирамиды.
6
4
О
ОС = 3
Ответ: 5
Высота правильной шестиугольной пирамиды равна 5

18. Высота правильной шестиугольной пирамиды равна 5. Боковое ребро наклонено к плоскости основания под углом 30°. Найдите боковое ребро пирамиды.
5
30°
О
AS = 2 · SO
Ответ: 10
Ответы на задачи. 1. 50 2. 2 3

Ответы на задачи.1. 502. 23. 454. 25. 26. 57. а) 2 б) 608. а) 3 б) 59. 310. 1411. 112. 613. 6014. 415. 216. 317. 518. 10
Подборка по базе: ЗАДАЧИ РЕШЕНИЕ.docx, права человека международз.docx, 10 кл право международная защита прав в военное время.docx, Жизненные циклы паразитов_ теория, задания на определение послед, Презентация для урока в 9 классе на тему Подготовка к ОГЭ. Решен, Практикум решение задач 8.docx, реферат международный менеджмент .docx, Типы взаимоотношений между организмами. Прямые и косвенные типы , ДИАЛОГ РЕШЕНИЕ.docx, МОРДА НА РЕШЕНИЕ КомГВ.docx
Задача № 5. Смежные кривые
По исходным данным задачи, определить расстояние между вершинами углов поворота смежных кривых и вычертить в масштабе 1:2000 их план, указав на нем все элементы кривых.
1. Принимаем II категорию железнодорожного пути.
2. Кривые расположены во второй зоне скоростей.
3. Длины переходных кривых выбираем из таблицы 7 методических указаний.
4. Смежные кривые направлены в разные стороны.
Исходные данные: α1 = 200, R1 = 1200 м, α2 = 300, R2 = 800 м.
Решение
Определяем минимальное расстояние между вершинами углов поворота смежных кривых по формуле:
LB = T1 + T2 + p1 + p2 + α
где: T1,T2 – тангенс круговых кривых, выбираем из таблицы для разбивки кривых
p1,p2 – длины для устройства переходных кривых
α – прямая вставка между смежными кривыми, выбираем из [1], с 41.
р = Тр + m.
где: Тр, m – определяем из [2].
Из таблицы 7 «Методических указаний» выбираем L1 = 100 м. По «Таблицам для разбивки кривых на железных дорогах» выбираем элементы круговой и переходной кривых: Т1 = 211.59 м, Б1 = 18.51 м, Тр1 = 0.06 м, m1 = 50.00 м, Бр1 = 0.35 м.
Аналогично выбираем элементы для второй кривой L2 = 140 м.: Т2 = 214.36 м, Б1 = 28.22 м, Тр2 = 0.26 м, m2 = 69,98 м, Бр = 1,05 м.
Из таблицы 5 «Изыскания и проектирования железных дорог» выбираем длину прямой вставки: а = 150 м.
LB = 211.59+ 214,36 + (0,06 + 50,00) + (0,26 + 69,98) + 50 = 696,25 м.
По исходным и расчетным данным вычерчиваем план кривых в масштабе 1:2000.
Задача 6. Определить минимально допустимое расстояние Х от перелома профиля до начала или конца кривой и вычертить пояснительную схему (без масштаба), указав на ней все числовые значения элементов профиля и плана.
По исходным данным таблицы с методических указаний определить минимально допустимое расстояние х от перелома профиля до начала или конца кривой и вычертить пояснительную схему, указав на ней все числовые значения элементов профиля и плана.
1. Принять I категорию железнодорожной линии.
2. Длину переходной кривой принять для меньшего радиуса из задачи 5 согласно I категории.
Исходные данные: i1 = -2 0/00, i2 = +13 0/00, i3 = -8 0/00,
Решение
Для обеспечения плавности хода железнодорожного транспорта элементы продольного профиля сопрягаются вертикальной кривой и эта кривая не должна накладываться на переходную кривую в плане. Минимальное расстояние Х определяется по формуле:
Х = ТВ + L/2,
где ТВ – тангенс вертикальной кривой:
ТВ = (RВ / 2000) ∙ Δ i,
где Δ i – алгебраическая разность уклонов в смежных элементах профиля;
RB – радиус вертикальной кривой.
Согласно СНиП для I категории RВ = 15000м. Из задачи 5 выбираем меньший радиус R2 = 800 м, а длина переходной кривой L = 180м (для I категории ж.д. линий), из таблицы 7 «Методических указаний».
Δ i1 = i1 – i2 = -2 – (+13) = -15 0/00
ТВ1 = (RВ / 2000) ∙ |Δi1| = (15000 / 2000) ∙ 15 = 112,5 м.
Х1 = ТВ1 + L/2 = 112,5 + 180 / 2 = 202.5 м.
Δ i2 = i1 – i2 = 13 – (-8) = +21 0/00
ТВ2 = (RВ / 2000) ∙ |Δi2| = (15000 / 2000) ∙ 21 = 157,5 м.
Х2 = ТВ2 + L/2 =157,5 + 180 / 2 = 247,5 м.
Задача 7. Составит утрированный продольный профиль в масштабах: горизонтальный 1:10000, вертикальный 1: 100. Провести реконструкцию профиля существующей железной дороги по нормам СНиП, при условии, что верхнее строение пути характеризуется следующими данными;
По исходным данным таблиц 6 и 8 методических указаний:
1. Составить утрированный продольный профиль на миллиметровой бумаге в масштабах: горизонтальный 1:1000; вертикальный 1:100.
2. Провести реконструкцию профиля существующей железной дороги по нормам СНиП, при условии, что верхнее строение пути характеризуется следующими данными:
1. песчаная подушка – h(п) = 0,20 м;
2. щебеночный слой – h(щ) = 0,25 м;
3. толщина шпалы – h(ш) = 0,15 м;
4. высота рельса Р -65 с подкладкой – h(р) = 0,20 м.
Итого мощность верхнего строения пути: НВСП = h(п) + h(щ) + h(ш) + h(р) = 0,20 + 0,25 + 0,15 + 0,20 = 0,80 м.
3. Нанести на профиль искусственные сооружения.
Исходные данные: металлический мост ПК 7, путепровод ПК17, начало кривой ПК11, угол поворота -11015′, радиус кривой R= 1200 м, длина переходной кривой L = 100 м.
Решение
7.1 За проектный уровень при проектировании новых железных дорог принимается бровка земляного полотна (БЗП), а на утрированном профиле при проектировании, реконструкции существующих железных дорог – проектную головку рельса (ПГР). На утрированном продольном профиле наносим линии: существующей головки рельса (СГР) – сплошная линия, низа балластного слоя (НБС) – штриховая линия и поверхности земли (З) – штрих – пунктирная.
7.2 По исходным данным на профиль наносятся: путепровод и металлический мост.
7. В графу «план существующего пути» предварительно рассчитав пикетажные значения конца кривой, наносится кривая: α-11015′, R= 1200 м, L = 100 м, Т = 118,19 м, К = 235,62 м, Тр = 0,04 м, m = 50,00 м – из таблиц для разбивки кривых.
Тс = Т + Тр + m = 118,19 + 0,04 + 50,00 = 168,23 м.
Кс = К + l = 235,62 + 100 = 335,62 м.
Пикетажное значение конца кривой будет равно:
КК = НК + Кс, т.е. ПК11 + 335,62 = 1435,62 м или ПК 14 + 35,62.
7.4 Вычисляем отметки расчетной головки рельса (РГР). РГРПК0 = НБСПК0 + НВСП = 48,37 + 0,8 = 49,17., и т.д.
7.5 Исправление профиля можно выполнить либо за счет подъемки, либо за счет срезки. Так как подъемку произвести легче, чем срезку, то проектное положение головки рельса (ПГР) необходимо запроектировать в основном только за счет подъемки. При этом нужно помнить, что величина подъемки ограничена шириной земляного полотна.
В некоторых случаях подъемку выполнить нельзя, например, на металлических мостах – отсутствует балласт; под путепроводами – нарушение верхнего габарита. В этих случаях существующие отметки головки рельса (СГР) сохраняются, а на подходах к ним приходиться выполнять срезку, которая технически оправдана. В остальных случаях ее следует избегать. Так же, следует помнить, что минимальная длина элементов профиля не менее 200 м.
7.6 При вычислении подъемки или срезки руководствуемся следующими условиями. Если линия ПГР выше или совпадает с линией РГР, то имеет место подъемка: П = ПГР – СГР, если ПГР ниже СГР имеет место срезка: С = РГР – ПГР.
ПК0: П = 49,18 – 48,65= 0,53 м и т.д.
7.7 Так же необходимо помнить, что при нанесении проектной линии в зоне переходных кривых не допускается перелома профиля.
7.8 Для обеспечения плавности движения поездов по профилю между его элементами при алгебраической разности уклонов Δ i ≥ 1,50/00 вписываются вертикальные кривые различных радиусов. Согласно СНиП для II категории RВ = 15000м.
Например на ПК2 между первым и вторым элементами профиля необходимо вписать вертикальную кривую, так как алгебраическая разность уклонов Δ i >1,50/00
Δ i1 = -5,0 – (-1,4) = -3,6 0/00.
ТВ1 = (RВ / 2000) ∙ |Δi1| = (15000 / 2000) ∙ 3,6 = 27 м.
Х1 = ТВ12 / 2 RВ = 27 2 / 2∙15000 = 0,02 м.
Литература
1. Кантор И.И., Пауль В.П. Основы проектирования и постройки железных дорог. М.: Транспорт , 1983.
2. Волков В.Н. «Геодезия», М., «Недра» , 2001-350 с.
3.Радионов В.И., Волков В.Н. «Задачник по геодезии», М., «Недра» , 1988 – 268 с.
4. Власов Д.И., Логинов В.Н. «Таблицы для разбивки кривых на железных дорогах», «Транспорт» , 1968 – 519 с.
Вариант № 15
Задача № 5. Смежные кривые
По исходным данным задачи, определить расстояние между вершинами углов поворота смежных кривых и вычертить в масштабе 1:2000 их план, указав на нем все элементы кривых.
1. Принимаем II категорию железнодорожного пути.
2. Кривые расположены во второй зоне скоростей.
3. Длины переходных кривых выбираем из таблицы 7 методических указаний.
4. Смежные кривые направлены в одну сторону.
Исходные данные: α1 = 220, R1 = 1500 м, α2 = 320, R2 = 700 м.
Решение
Определяем минимальное расстояние между вершинами углов поворота смежных кривых по формуле:
LB = T1 + T2 + p1 + p2 + α
где: T1,T2 – тангенс круговых кривых, выбираем из таблицы для разбивки кривых
p1,p2 – длины для устройства переходных кривых
α – прямая вставка между смежными кривыми, выбираем из [1], с 41.
р = Тр + m.
где: Тр, m – определяем из [2].
Из таблицы 7 «Методических указаний» выбираем L1 = 80 м. По «Таблицам для разбивки кривых на железных дорогах» выбираем элементы круговой и переходной кривых: Т1 = 291.57 м, Б1 = 28.08 м, Тр1 = 0.04 м, m= 40,00 м, Бр = 0,18 м.
Аналогично выбираем элементы для второй кривой L2 = 160 м.: Т2 = 200.72 м, Б1 = 28,21 м, Тр = 0.45 м, m= 79.97 м, Бр = 1.59 м.
Из таблицы 5 «Изыскания и проектирования железных дорог» выбираем длину прямой вставки: а = 150 м.
LB = 291,57 + 200.72 + (0.04 + 40.00) + (0,45 + 79.97) + 150 = 762,75 м.
По исходным и расчетным данным вычерчиваем план кривых в масштабе 1:2000.
Задача 6. Определить минимально допустимое расстояние Х от перелома профиля до начала или конца кривой и вычертить пояснительную схему (без масштаба), указав на ней все числовые значения элементов профиля и плана.
По исходным данным таблицы с методических указаний определить минимально допустимое расстояние х от перелома профиля до начала или конца кривой и вычертить пояснительную схему, указав на ней все числовые значения элементов профиля и плана.
1. Принять I категорию железнодорожной линии.
2. Длину переходной кривой принять для меньшего радиуса из задачи 5 согласно I категории.
Исходные данные: i1 = – 30/00, i2 = +11 0/00, i3 = -9 0/00,
Решение
Для обеспечения плавности хода железнодорожного транспорта элементы продольного профиля сопрягаются вертикальной кривой и эта кривая не должна накладываться на переходную кривую в плане. Минимальное расстояние Х определяется по формуле:
Х = ТВ + L/2,
где ТВ – тангенс вертикальной кривой:
ТВ = (RВ / 2000) ∙ Δ i,
где Δ i – алгебраическая разность уклонов в смежных элементах профиля;
RB – радиус вертикальной кривой.
Согласно СНиП для I категории RВ = 15000м. Из задачи 5 выбираем меньший радиус R2 = 700 м, а длина переходной кривой L = 180м (для I категории ж.д. линий), из таблицы 7 «Методических указаний».
Δ i1 = i1 – i2 = -3 – (+11) = -14 0/00
ТВ1 = (RВ / 2000) ∙ |Δi1| = (15000 / 2000) ∙ 14 = 105 м.
Х1 = ТВ1 + L/2 = 105 + 180 / 2 = 195 м.
Δ i2 = i1 – i2 = +11 – (-9) = +21 0/00
ТВ2 = (RВ / 2000) ∙ |Δi2| = (15000 / 2000) ∙ 21 = 157,5 м.
Х2 = ТВ2 + L/2 = 157,5 + 180 / 2 = 247,5 м.
Задача 7. Составит утрированный продольный профиль в масштабах: горизонтальный 1:10000, вертикальный 1: 100. Провести реконструкцию профиля существующей железной дороги по нормам СНиП, при условии, что верхнее строение пути характеризуется следующими данными;
По исходным данным таблиц 6 и 8 методических указаний:
1. Составить утрированный продольный профиль на миллиметровой бумаге в масштабах: горизонтальный 1:1000; вертикальный 1:100.
2. Провести реконструкцию профиля существующей железной дороги по нормам СНиП, при условии, что верхнее строение пути характеризуется следующими данными:
1. песчаная подушка – h(п) = 0,20 м;
2. щебеночный слой – h(щ) = 0,25 м;
3. толщина шпалы – h(ш) = 0,15 м;
4. высота рельса Р -65 с подкладкой – h(р) = 0,20 м.
Итого мощность верхнего строения пути: НВСП = h(п) + h(щ) + h(ш) + h(р) = 0,20 + 0,25 + 0,15 + 0,20 = 0,80 м.
3. Нанести на профиль искусственные сооружения.
Исходные данные: металлический мост ПК 5, путепровод ПК14, начало кривой ПК15, угол поворота -12012′, радиус кривой R= 800 м, длина переходной кривой L = 140 м.
Решение
7.1 За проектный уровень при проектировании новых железных дорог принимается бровка земляного полотна (БЗП), а на утрированном профиле при проектировании, реконструкции существующих железных дорог – проектную головку рельса (ПГР). На утрированном продольном профиле наносим линии: существующей головки рельса (СГР) – сплошная линия, низа балластного слоя (НБС) – штриховая линия и поверхности земли (З) – штрих – пунктирная.
7.2 По исходным данным на профиль наносятся: путепровод и металлический мост.
7. В графу «план существующего пути» предварительно рассчитав пикетажные значения конца кривой, наносится кривая: α-12012′, R= 800 м, L = 140 м, Т = 85,50 м, К = 170,34 м, Тр = 0,12 м, m = 69,98 м – из таблиц для разбивки кривых.
Тс = Т + Тр + m = 85,50 + 0,12 + 69,98 = 155,6 м.
Кс = К + l = 170,34+ + 140 = 310,34 м.
Пикетажное значение конца кривой будет равно:
КК = НК + Кс, т.е. ПК15 + 310,34 = 1810,34 м или ПК 18 + 10,34.
7.4 Вычисляем отметки расчетной головки рельса (РГР). РГРПК0 = НБСПК0 + НВСП = 63,83 + 0,8 = 64,63., и т.д.
7.5 Исправление профиля можно выполнить либо за счет подъемки, либо за счет срезки. Так как подъемку произвести легче, чем срезку, то проектное положение головки рельса (ПГР) необходимо запроектировать в основном только за счет подъемки. При этом нужно помнить, что величина подъемки ограничена шириной земляного полотна.
В некоторых случаях подъемку выполнить нельзя, например, на металлических мостах – отсутствует балласт; под путепроводами – нарушение верхнего габарита. В этих случаях существующие отметки головки рельса (СГР) сохраняются, а на подходах к ним приходиться выполнять срезку, которая технически оправдана. В остальных случаях ее следует избегать. Так же, следует помнить, что минимальная длина элементов профиля не менее 200 м.
7.6 При вычислении подъемки или срезки руководствуемся следующими условиями. Если линия ПГР выше или совпадает с линией РГР, то имеет место подъемка: П = ПГР – СГР, если ПГР ниже СГР имеет место срезка: С = РГР – ПГР.
ПК0 П = 64,64 – 64,31= 0,32 м и т.д.
7.7 Так же необходимо помнить, что при нанесении проектной линии в зоне переходных кривых не допускается перелома профиля.
7.8 Для обеспечения плавности движения поездов по профилю между его элементами при алгебраической разности уклонов Δ i ≥ 1,50/00 вписываются вертикальные кривые различных радиусов. Согласно СНиП для II категории RВ = 15000м.
Например на ПК2 между первым и вторым элементами профиля необходимо вписать вертикальную кривую, так как алгебраическая разность уклонов Δ i >1,50/00
Δ i1 = -3,0 – 0 = -3,3 0/00.
ТВ1 = (RВ / 2000) ∙ |Δi1| = (15000 / 2000) ∙ 3,3 = 24.75 м.
Х1 = ТВ12 / 2 RВ = 24.75 2 / 2∙15000 = 0,02 м.
Литература
1. Кантор И.И., Пауль В.П. Основы проектирования и постройки железных дорог. М.: Транспорт , 1983.
2. Волков В.Н. «Геодезия», М., «Недра» , 2001-350 с.
3.Радионов В.И., Волков В.Н. «Задачник по геодезии», М., «Недра» , 1988 – 268 с.
4. Власов Д.И., Логинов В.Н. «Таблицы для разбивки кривых на железных дорогах», «Транспорт» , 1968 – 519 с.
Затем
определяем пикетажное положение основных точек закругления в соответствии с
рисунком 3.1. Поскольку нам известно положение НКК, то сначала определим
положение НЗ.
–
начала закругления (НЗ)
–
конец круговой кривой (ККК)
|
ПК ККК: ПК НЗ+L+К1; |
(3.11) |
–
конец закругления (КЗ)
|
ПК КЗ: ПК НЗ+2×L+К1; |
(3.12) |
–
после этого определим положение ПК ВУП,
|
ПК ВУП: ПК НЗ+(T+t)-Д/2; |
(3.13) |
Результаты расчётов заносятся в ведомость углов
поворотов, правильность составления которой контролируется системой проверок:
|
|
(3.14) |
|
|
где ∑К |
– суммарная длина криволинейных |
|
|
∑П |
– |
|
|
Lтр |
– длина трассы, м; |
|
|
|
(3.15) |
|
|
где ∑S |
– суммарное расстояние между вершинами |
|
Произведём расчёт существующей трассы по второму углу
с радиусом 350 м.
Для существующей дороги принимаем элементы круговой
кривой в соответствии с [4, с.13, табл.3.1], таким образом:
– L=80 м;
– 2b=13°10¢;
– t=39,987 м;
– p=0,76 м.
Поскольку ![]() , т. е. условие 3.4
, т. е. условие 3.4
выполняется, то возможно устройство вертикальной кривой.
Произведём расчёты по формулам (3.5) – (3.13):
|
–
– при g=18°-13°10¢=4°50¢; |
|
|
|
–
биссектрисы – Б
|
|
–
полную длину закругления
|
|
–
домер
|
|
Затем
определим пикетажное положение основных точек закругления:
–
начала закругления (НЗ)
|
ПК НЗ: ПК 467+24-80=ПК 466+44; |
–
конец круговой кривой (ККК)
|
ПК ККК: ПК 466+44+80+29,93=ПК 467+53,93; |
–
конец закругления (КЗ)
|
ПК КЗ: ПК 466+44+2×80+29,93=ПК |
–
пикетажное положение вершина кривой
(ВУП) определяем следующим образом:
|
ПК НЗ: ПК 466+44 |
ПК КЗ: ПК 468+33,93 |
|
+Т=55,43 м |
-Т=55,43 м |
|
+t=39,98 м |
-t=39,98 м |
|
-Д2/2=0,89/2=0,445 |
+Д2/2=0,89/2=0,445 |
|
ВУП 2 ПК 467+38,965; |
ВУП 2 ПК 467+38,965. |
Расчёт первого угла поворота производиться
аналогично, результаты представлены в таблице 3.1.
Определим расстояние
между ВУ следующим образом:
|
S1 |
S2 |
S3 |
|
ПК ВУП 1: ПК 456+80,9 |
ПК ВУП 2: ПК 467+38,965 |
КХ ПК 480+00 |
|
– НХ ПК 450+00 |
-ПК ВУП 1: ПК 456+80,9 |
-ПК ВУП 2: |
|
+Д1/2=1,5/2=0,75 |
+(Д1+Д2)/2=(1,5+0,89)/2=1,195 |
+Д2/2=0,89/2=0,445 |
|
681,65 м; |
1059,26 м; |
1261,48 м. |
Длина
прямых определяется как
|
П : ПК НЗn-ПК КЗn-1; |
(3.16) |
Получаем
|
П1 |
П2 |
П3 |
|
ПК НЗ: ПК 455+50 |
ПК НЗ 2: ПК 466+44 |
КХ: ПК 480+00 |
|
– НХ ПК 450+00 |
-ПК КЗ 1: ПК 458+11,80 |
– ПК КЗ2: ПК 468+33,93 |
|
550 м; |
832,20 м; |
1166,07 м. |
Результаты расчётов сводим в ведомость углов
поворотов (таблица 3.1), правильность
составления которой контролируем системой проверок по формулам 3.14 и
3.15:
|
|
Проверка выполняется.
|
681,65+1059,26+1261,48-1,50-0,89=3000м. |
Проверка также выполняется, что свидетельствует о
правильности произведённых расчётов.
3.2. Увеличение радиусов кривых ВУП 1
– ПК 456+81,65 и ВУП 2 – ПК 467+39,41.
При
реконструкции производится увеличение радиуса ВУП 2 – ПК 467+39,41 с 350 м до 700 м и кроме того, в соответствии с [3, с.11,
табл.14] возрастает длина переходной кривой с 80 м до 110 м, а для ВУП 1 – ПК 456+81,65 появляется переходная
кривая длиной 100 м.
Произведём расчёты для
радиуса 700м.
Элементы
переходных кривых рассчитаем по
формулам (3.1) – (3.3):
–
угол поворота 2b:
|
|
–
сдвижка начала круговой кривой – t:
|
|
–
сдвижка круговой кривой за счёт
устройства переходной – p:
|
|
|
|
|
Произведём расчёты по формулам (3.5) – (3.13):
|
–
– при угле g=18°-9°00¢=9°00¢; |
|
|
|
–
биссектрисы – Б
|
|
–
полную длину закругления
|
|
–
домер
|
|
Затем
определяем пикетажное положение основных точек закругления:
|
ВУП 2 ПК 467+38,965 |
ВУП 2 ПК 467+38,965 |
|
|
-Т=110,87 м |
+Т=55,43 м |
|
|
-t=54,99 м |
+t=39,98 м |
|
|
+Д1/2=0,89/2=0,445 |
-Д1/2=0,89/2=0,445 |
|
|
ПК НЗ: ПК 465+73,55 |
ПК КЗ: ПК 469+04,38 |
|
|
+L=110 м |
-L=110 м |
|
|
ПК НКК: ПК 466+83,55. |
ПК ККК: ПК 467+94,38. |
|
|
К1′ |
ПК 467+94,38- ПК 466+83,55=110,83 |
|
|
-К1 |
109,96 |
|
|
Δ |
0,87 |
|
Таким
образом в пределах переходной кривой появляется резанный пикет на величину 0,87 м.
Определим
длину прямых по формуле 3.17.
|
П1 |
П2 |
П3 |
|
ПК НЗ: ПК |
ПК НЗ2: ПК |
КХ ПК 480+00 |
|
– НХ ПК |
-ПК КЗ1: ПК |
– ПК КЗ2: |
|
500,01 м; |
711,76 м; |
1095,62 м. |
Расчёт первого угла поворота производиться
аналогично, результаты также представлены в таблице 3.2.
На основании расчётов производим построение плана
трассы, нанося на него существующую (черного цвета) и проектную (красного цвета) линии.
Собрание уникальных книг, учебных материалов и пособий, курсов лекций и отчетов по геодезии, литологии, картированию, строительству, бурению, вулканологии и т.д.
Библиотека собрана и рассчитана на инженеров, студентов высших учебных заведений по соответствующим специальностям. Все материалы собраны из открытых источников.
Разбивка трассы.
Закрепление и измерение углов. Выбранную трассу надёжно закрепляют на местности. Вершину угла, образуемого прямыми линиями трассы, закрепляют забиваемым вровень с поверхностью земли колом (рис. 15.1, а). На расстоянии 1 м от кола с внешней стороны угла на его биссектрисе устанавливают столб с затёсом. На затёсе, обращённом в сторону вершины угла, делают надпись, указывающую номер вершины угла, год, угол поворота трассы, радиус вписываемой в угол кривой, расстояние от начала трассы. Измеряют расстояния от вершины угла до расположенных вблизи приметных местных предметов (дерево, угол здания, валун и др.) и показывают их на абрисе – схеме, составляемой для облегчения отыскания вершины угла в последующем, особенно в случае разрушения опознавательного столба.
Над колом, закрепляющим вершину угла, устанавливают теодолит и измеряют лежащий справа по ходу трассы угол b между направлениями на соседние вершины углов. Измерение выполняют одним приёмом с точностью 0,5¢. Угол поворота трассы (рис. 15.2) вычисляют по формулам:
αпр = 180°– b2 (при повороте трассы вправо: b < 180°) или
αлев = b3 – 180° (при повороте трассы влево: b > 180°).
Для контроля буссолью измеряют магнитные азимуты линий.
б)
а)
![inj_geo_2-112.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_2-112.jpg)
Рис. 15.1 Закрепление точек на трассе:
а – закрепление вершины угла: 1 – кол; 2 – столб;
б – закрепление пикета и плюса: 1 – кол; 2 – сторожок
![inj_geo_2-113.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_2-113.jpg)
Рис. 15.2 Углы поворота трассы
Разбивка пикетажа и измерение длин линий. Расстояния между вершинами углов поворота трассы измеряют светодальномером или мерной лентой. Измерение выполняют дважды с предельной относительной погрешностью измерений не более 1:1000-1:2000. В ходе одного из измерений трассу разбивают на отрезки длиной 100 метров по горизонтальному проложению. Конец каждого отрезка – пикет; его закрепляют, забивая вровень с землёй кол. Впереди него по ходу трассы на расстоянии 20-25 см забивают второй, возвышающийся над поверхностью земли кол – сторожок (рис. 15.1, б). На сторожке надписывают порядковый номер пикета, например, ПК13, что означает: номер пикета – 13, расстояние от начала трассы – 1300 м.
Чтобы получить 100-метровые горизонтальные проложения, следует, учитывая наклон местности, увеличивать длину откладываемых наклонных отрезков. Поэтому в них вводят поправки за наклон со знаком плюс. Часто вместо введения поправок, натягивая мерную ленту, удерживают её в горизонтальном положении и проектируют отвесом её приподнятый конец на землю. Чтобы лента меньше провисала, поддерживают её в середине.
Кроме пикетов, колышком и сторожком закрепляют плюсовые точки (или просто “плюсы”), где на трассе изменяется наклон местности. На сторожке в этом случае пишут номер предыдущего пикета и расстояние от него в метрах, например ПК13+46, что означает 46 м после пикета № 13 или 1346 м от начала пикетажа.
Плюсовыми точками фиксируют также места пересечения трассой любых сооружений, дорог, линий связи, водотоков, границ угодий и т. д.
Поперечники. Там, где местность имеет заметный (более 1:5) поперечный уклон, на каждом пикете и плюсовой точке разбивают перпендикуляры к трассе, называемые поперечниками. Поперечники разбивают в обе стороны длиной 15-30 м с таким расчётом, чтобы обеспечить съёмкой всю ширину полосы местности под будущие сооружения дороги (земляное полотно, водоотводные устройства, здания и пр.). Конечные точки поперечника закрепляют точкой и сторожком, плюсовые точки, располагаемые в местах изменения наклона местности, – только сторожком. На сторожках пишут расстояние от оси трассы с буквой “П” (справа от оси трассы) или “Л” (слева от оси трассы).
Плановая привязка трассы. Начало и конец трассы привязывают к пунктам государственной геодезической сети, например, с помощью теодолитных ходов. В результате измеренные на трассе углы и расстояния совместно с ходами привязки образуют единый разомкнутый теодолитный ход. Это позволяет проконтролировать правильность выполненных линейных и угловых измерений и вычислить координаты вершин углов поворота трассы.
На длинной трассе привязку к государственной геодезической сети выполняют не реже чем через 25 км, а при удалении пунктов от трассы более чем на 3 км – не реже чем через 50 км.
Съёмка полосы местности. В ходе разбивки пикетажа выполняют съёмку ситуации в полосе местности шириной по 100 м в обе стороны от оси трассы. При этом полосу шириной 25 м вправо и влево снимают инструментально – главным образом, методом перпендикуляров, а дальше – глазомерно. Результаты съёмки в виде абриса масштаба 1:2000 заносят в пикетажный журнал, изготовляемый из листов миллиметровой бумаги размером 10´15 см.
По середине листа проводят вертикальную прямую, изображающую ось трассы. На ней штрихами отмечают положение пикетов и плюсов и рядом подписывают их значения. Каждая новая страница начинается с пикета, которым закончена предыдущая. В местах поворота трассы стрелкой показывают направление поворота и надписывают румб следующей прямой. На свободном месте пишут основные элементы кривой. Показывают расстояния от местных предметов до оси трассы и габариты строений. Делают записи о типе дорог, характеристике леса, карьерах – обо всём, что может иметь значение для предстоящего строительства.
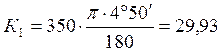 м;
м;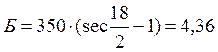 ;
;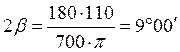 ;
;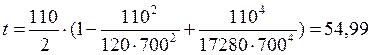 м;
м;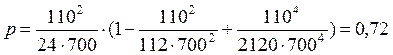 м.
м.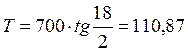 м;
м;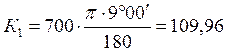 м;
м;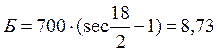 .
.