Как найти расстояние от этой точки трапеции

Задача

В равнобедренную трапецию, периметр которой 220, а площадь равна 2420, можно вписать окружность.

Найти расстояние от точки пересечения диагоналей трапеции до её меньшего основания.

Дано: ABCD — трапеция,

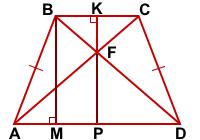
AD || BC, AB=CD,

P_ABCD=220, S_ABCD=2420,

AC∩BC=F, FK⊥BC

Найти: FK

Решение:

Так как в трапецию ABCD можно вписать окружность, то AD+BC=AB+CD.

Так как AB=CD, то AD+BC=2AB.

P_ABCD=AD+BC+AB+CD=4AB=2(AD+BC)=220.

Следовательно, AB=55, AD+BC=110.

Проведём через точки B и F высоты KP и BM.

   

   

Из прямоугольного треугольника ABM по теореме Пифагора

   

   

По свойству равнобедренной трапеции,

   

   

   

Рассмотрим треугольники AFD и CFB.

∠DAF=∠BCF (как внутренние односторонние при AD || BC и секущей AC),

∠FAD=∠FCB (как смежные).

Следовательно, треугольники AFD и CFB подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих элементов:

   

Пусть FK=x, тогда FP=44-x,

   

Ответ: 8,8.

Вы находитесь на странице вопроса Основа прямоугольный трапеции равна 10 см и 15 см? из категории Геометрия.
Уровень сложности вопроса рассчитан на учащихся 10 – 11 классов. На странице
можно узнать правильный ответ, сверить его со своим вариантом и обсудить
возможные версии с другими пользователями сайта посредством обратной связи.
Если ответ вызывает сомнения или покажется вам неполным, для проверки
найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте
новый вопрос, используя ключевые слова: введите вопрос в поисковую строку,
нажав кнопку в верхней части страницы.

Здравствуйте, уважаемые читатели. В этот раз разберем следующую задачу:

В равнобедренную трапецию, периметр которой равен 80, а площадь
равна 320, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.

Выполним построение рисунка и напишем, что нам известно:

Если в четырехугольник вписана окружность, то суммы противоположных сторон равны.

1) Найдем боковые стороны трапеции АВ и CD. Обратимся к условию задачи. Нам известен периметр трапеции. Периметр – это сумма все сторон многоугольника.

Так как в первом выражении у нас получилось, что 2АВ=ВС+АD, подставим это в периметр и найдем боковые стороны АВ и СD:

Зная размеры боковых сторон, найдем сумму оснований:

2) Зная площадь трапеции, найдем высоту КF:

Все что было нам известно по условию задачи, мы использовали. Теперь, чтобы найти отрезок ОК, необходимо узнать в каком отношении точка О делит высоту трапеции KF. Для этого рассмотрим треугольники ВОС и DОA. Эти треугольники подобны.

Если узнаем отношение оснований BC:DA, то найдем отношение КО:OF

3) Проведем высоты BH и CN, рассмотрим прямоугольный треугольник ABH, по теореме Пифагора найдем AH:

4) Теперь найдем основания трапеции ВС и AD:

5) Найдем отношение оснований трапеции и отрезок ОК

Если вы знаете способ решения легче, пишите в комментариях.

Спасибо что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.

Радиус описанной окружности трапеции

Как найти радиус описанной окружности для трапеции?

В зависимости от данных условия, сделать это можно разными способами. Готовой формулы радиуса описанной около трапеции окружности нет.

I. Радиус описанной около трапеции окружности как радиус окружности, описанной около треугольника, вершины которого — вершины трапеции

Описанная около трапеции окружность проходит через все её вершины, следовательно, является описанной для любого из треугольников, вершины которых являются вершинами трапеции.

В общем случае радиус описанной около треугольника окружности может быть найден по одной из формул

где a — сторона треугольника, α — противолежащий ей угол;

либо по формуле

где a, b, c — стороны, S — площадь треугольника.

Для трапеции ABCD радиус может быть найден, например, как радиус окружности, описанной около треугольника ABD:

где синус угла A можно найти из прямоугольного треугольника ABF:

III. Радиус описанной около трапеции окружности как расстояние до точки пересечения серединных перпендикуляров

Радиус описанной окружности — точка пересечения серединных перпендикуляров с сторонам трапеции. (Можно рассуждать иначе: в равнобедренном треугольнике AOD (AO=OD=R) высота ON является также медианой. Для треугольника BOC — аналогично).

Если известна высота трапеции KN=h, основания AD=a, BC=b, можно обозначить ON=x.

Если центр окружности лежит внутри трапеции, OK=h-x, из прямоугольных треугольников ANO и BKO можно выразить

и приравнять правые части

Решив это уравнения относительно x, можно найти R.

IV. Если диагональ трапеции перпендикулярна боковой стороне, центр описанной окружности лежит на середине большего основания и радиус равен половине большего основания.

точка O — середина AD

Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной окружности лежит вне трапеции, за большим основанием.

I вариант нахождения радиуса для этого случая не изменяется.

Во II случае OK=h+x, соответственно, изменяется уравнение для нахождения x и R.

Позже рассмотрим конкретные задачи нахождения радиуса описанной около трапеции окружности.

В равнобедренную трапецию вписана окружность. Расстояние от центра окружности до точки пересечения диагоналей трапеции относится к радиусу, как 3 : 5. Найдите отношение периметра трапеции к длине вписанной окружности.

Пусть O — центр окружности, P — точка касания с боковой стороной AB, F и T — точки касания окружности с основаниями AD и BC, M — середина AB, K — точка пересечения диагоналей AC и BD трапеции. Обозначим OK = 3x, OP = 5x.

Поскольку AP : PB = AF : BT = AK : KC, то KP || BC || OM. Из прямоугольного треугольника OKP находим, что KP = 4x. Из подобия треугольников OKP и MPO находим, что

OM = = .

Тогда периметр трапеции равен 8OM = 50x. Следовательно, искомое отношение равно

= .

Ответ

.

Трапеция. Свойства трапеции

Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .

Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .

Свойства трапеции

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.

Коэффициент подобия –

Отношение площадей этих треугольников есть .

4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.

5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.

7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

Свойства и признаки равнобедренной трапеции

1. В равнобедренной трапеции углы при любом основании равны.

2. В равнобедренной трапеции длины диагоналей равны.

3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.

4. Около равнобедренной трапеции можно описать окружность.

5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Вписанная окружность

Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то

Площадь

или где – средняя линия

Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

[spoiler title=”источники:”]

http://gitun.com/q/18022

[/spoiler]