Содержание
- Как определить расстояние от линзы до предмета
- Как определить расстояние от линзы до предмета
- Оптика. Линза. Фокусное расстояние линзы.
- Формула тонкой линзы
Линзой называется прозрачное тело, ограниченное двумя сферическими поверхностями. Если толщина самой линзы мала по сравнению с радиусами кривизны сферических поверхностей, то линзу называют тонкой .
Линзы входят в состав практически всех оптических приборов. Линзы бывают собирающими и рассеивающими . Собирающая линза в середине толще, чем у краев, рассеивающая линза, наоборот, в средней части тоньше (рис. 3.3.1).
Прямая, проходящая через центры кривизны и сферических поверхностей, называется главной оптической осью линзы. В случае тонких линз приближенно можно считать, что главная оптическая ось пересекается с линзой в одной точке, которую принято называть оптическим центром линзы . Луч света проходит через оптический центр линзы, не отклоняясь от первоначального направления. Все прямые, проходящие через оптический центр, называются побочными оптическими осями .
Если на линзу направить пучок лучей, параллельных главной оптической оси, то после прохождения через линзу лучи (или их продолжения) соберутся в одной точке , которая называется главным фокусом линзы. У тонкой линзы имеются два главных фокуса, расположенных симметрично на главной оптической оси относительно линзы. У собирающих линз фокусы действительные, у рассеивающих – мнимые. Пучки лучей, параллельных одной из побочных оптических осей, после прохождения через линзу также фокусируются в точку , которая расположена при пересечении побочной оси с фокальной плоскостью , то есть плоскостью, перпендикулярной главной оптической оси и проходящей через главный фокус (рис. 3.3.2). Расстояние между оптическим центром линзы и главным фокусом называется фокусным расстоянием. Оно обозначаетcя той же буквой .
Основное свойство линз – способность давать изображения предметов . Изображения бывают прямыми и перевернутыми , действительными и мнимыми , увеличенными и уменьшенными .
Положение изображения и его характер можно определить с помощью геометрических построений. Для этого используют свойства некоторых стандартных лучей, ход которых известен. Это лучи, проходящие через оптический центр или один из фокусов линзы, а также лучи, параллельные главной или одной из побочных оптических осей. Примеры таких построений представлены на рис. 3.3.3 и 3.3.4.
Следует обратить внимание на то, что некоторые из стандартных лучей, использованных на рис. 3.3.3 и 3.3.4 для построения изображений, не проходят через линзу. Эти лучи реально не участвуют в образовании изображения, но они могут быть использованы для построений.
Положение изображения и его характер (действительное или мнимое) можно также рассчитать с помощью формулы тонкой линзы . Если расстояние от предмета до линзы обозначить через , а расстояние от линзы до изображения через , то формулу тонкой линзы можно записать в виде:
Величину , обратную фокусному расстоянию. называют оптической силой линзы. Единицой измерения оптической силы является диоптрия (дптр). Диоптрия – оптическая сила линзы с фокусным расстоянием :
Формула тонкой линзы аналогична формуле сферического зеркала. Ее можно получить для параксиальных лучей из подобия треугольников на рис. 3.3.3 или 3.3.4.
Фокусным расстояниям линз принято приписывать определенные знаки: для собирающей линзы , для рассеивающей .
Величины и также подчиняются определенному правилу знаков:
и – для действительных предметов (то есть реальных источников света, а не продолжений лучей, сходящихся за линзой) и изображений;
и – для мнимых источников и изображений.
Для случая, изображенного на рис. 3.3.3, имеем: (линза собирающая), (действительный предмет).
По формуле тонкой линзы получим: следовательно, изображение действительное.
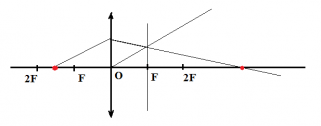
В случае, изображенном на рис. 3.3.4, (линза рассеивающая), (действительный предмет), то есть изображение мнимое.
В зависимости от положения предмета по отношению к линзе изменяются линейные размеры изображения. Линейным увеличением линзы Γ называют отношение линейных размеров изображения и предмета . Величине , как и в случае сферического зеркала, удобно приписывать знаки плюс или минус в зависимости от того, является изображение прямым или перевернутым. Величина всегда считается положительной. Поэтому для прямых изображений , для перевернутых . Из подобия треугольников на рис. 3.3.3 и 3.3.4 легко получить формулу для линейного увеличения тонкой линзы:
В рассмотренном примере с собирающей линзой (рис. 3.3.3): , следовательно, – изображение перевернутое и уменьшенное в 2 раза.
В примере с рассеивающей линзой (рис. 3.3.4): , ; следовательно, – изображение прямое и уменьшенное в 3 раза.
Оптическая сила линзы зависит как от радиусов кривизны и ее сферических поверхностей, так и от показателя преломления материала, из которого изготовлена линза. В курсах оптики доказывается следующая формула:
Радиус кривизны выпуклой поверхности считается положительным, вогнутой – отрицательным. Эта формула используется при изготовлении линз с заданной оптической силой.
Во многих оптических приборах свет последовательно проходит через две или несколько линз. Изображение предмета, даваемое первой линзой, служит предметом (действительным или мнимым) для второй линзы, которая строит второе изображение предмета. Это второе изображение также может быть действительным или мнимым. Расчет оптической системы из двух тонких линз сводится к двукратному применению формулы линзы, при этом расстояние от первого изображения до второй линзы следует положить равным величине , где – расстояние между линзами. Рассчитанная по формуле линзы величина определяет положение второго изображения и его характер ( – действительное изображение, – мнимое). Общее линейное увеличение Γ системы из двух линз равно произведению линейных увеличений обеих линз: . Если предмет или его изображение находятся в бесконечности, то линейное увеличение утрачивает смысл.
Частным случаем является телескопический ход лучей в системе из двух линз, когда и предмет, и второе изображение находятся на бесконечно больших расстояниях. Телескопический ход лучей реализуется в зрительных трубах – астрономической трубе Кеплера и земной трубе Галилея (см. § 3.5).
Тонкие линзы обладают рядом недостатков, не позволяющих получать высококачественные изображения. Искажения, возникающие при формировании изображения, называются аберрациями . Главные из них – сферическая и хроматическая аберрации. Сферическая аберрация проявляется в том, что в случае широких световых пучков лучи, далекие от оптической оси, пересекают ее не в фокусе. Формула тонкой линзы справедлива только для лучей, близких к оптической оси. Изображение удаленного точечного источника, создаваемое широким пучком лучей, преломленных линзой, оказывается размытым.
Хроматическая аберрация возникает вследствие того, что показатель преломления материала линзы зависит от длины волны света λ. Это свойство прозрачных сред называется дисперсией. Фокусное расстояние линзы оказывается различным для света с разными длинами волн, что приводит к размытию изображения при использовании немонохроматического света.
В современных оптических приборах применяются не тонкие линзы, а сложные многолинзовые системы, в которых удается приближенно устранить различные аберрации.
Формирование собирающей линзой действительного изображения предмета используется во многих оптических приборах, таких как фотоаппарат, проектор и т. д.
Фотоаппарат представляет собой замкнутую светонепроницаемую камеру. Изображение фотографируемых предметов создается на фотопленке системой линз, которая называется объективом . Специальный затвор позволяет открывать объектив на время экспозиции.
Особенностью работы фотоаппарата является то, что на плоской фотопленке должны получаться достаточно резкими изображения предметов, находящихся на разных расстояниях.
В плоскости фотопленки получаются резкими только изображения предметов, находящихся на определенном расстоянии. Наведение на резкость достигается перемещением объектива относительно пленки. Изображения точек, не лежащих в плоскости резкого наведения, получаются размытыми в виде кружков рассеяния. Размер этих кружков может быть уменьшен путем диафрагмирования объектива, т.е. уменьшения относительного отверстия (рис. 3.3.5). Это приводит к увеличению глубины резкости.
Проекционный аппарат предназначен для получения крупномасштабных изображений. Объектив проектора фокусирует изображение плоского предмета (диапозитив ) на удаленном экране (рис. 3.3.6). Система линз , называемая конденсором , предназначена для того, чтобы сконцентрировать свет источника на диапозитиве. На экране создается действительное увеличенное перевернутое изображение. Увеличение проекционного аппарата можно менять, приближая или удаляя экран с одновременным изменением расстояния между диапозитивом и объективом .
Оптика. Линза. Фокусное расстояние линзы.
Фокусное расстояние линзы — это дистанция между оптическим центром линзы и ее главным фокусом. Линзу относят к положительной (собирающей), когда ее фокусное расстояние больше нуля (F>0), и отрицательной (рассеивающей), когда ее фокусное расстояние менее нуля (F<0).
Формула фокусного расстояния для тонкой линзы записывается нижеследующим образом.
Когда линза рассеивающая — фокусное расстояние (f) будет со знаком « — ». Для реального изображения от реального объекта в собирающей линзе — эти параметры будут со знаком «+». Важно помнить, что указываем знак минус при рассмотрении расстояния до мнимого изображения. С тем же знаком будет и дистанция от мнимого объекта.
Когда возникает потребность вычислить фокусное расстояние для любой линзы, формула несколько усложняется:
где F — фокусное расстояние линзы;
d — дистанция от объекта, до линзы;
f — дистанция от линзы, до изображения;
n — относительный показатель преломления;
R1 — радиус кривизны передней части линзы;
R2 — радиус кривизны задней части линзы.
Формула тонкой линзы
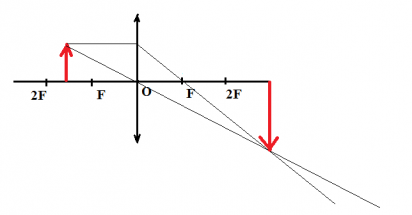
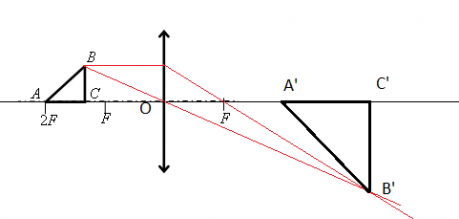
Установим соответствие между геометрическим и алгебраическим способами описания характеристик изображений, даваемых линзами. Сделаем чертёж по рисунку со статуэткой в предыдущем параграфе.
Поясним наши обозначения. Фигура AB – статуэтка, которая находится на расстоянии d от тонкой собирающей линзы с центром в точке О. Правее располагают экран, на котором A’B’ – изображение статуэтки, наблюдаемое на расстоянии f от центра линзы. Точками F обозначены главные фокусы, а точками 2F – двойные фокусные расстояния.
Почему мы построили лучи именно так? От головы статуэтки параллельно главной оптической оси идёт луч BC, который при прохождении линзы преломляется и проходит через её главный фокус F, создавая луч CB’. Каждая точка предмета испускает множество лучей. Однако при этом луч BO, идущий через центр линзы, сохраняет направление из-за симметрии линзы. Пересечение преломлённого луча и луча, сохранившего направление, даёт точку, где будет изображение головы статуэтки. Луч AO, проходящий через точку О и сохраняющий своё направление, позволяет нам понять положение точки A’, где будет изображение ног статуэтки – на пересечении с вертикальной линией от головы.
Предлагаем вам самостоятельно доказать подобие треугольников OAB и OA’B’, а также OFC и FA’B’. Из подобия двух пар треугольников, а также из равенства OC=AB, имеем:
Последняя формула предсказывает соотношение между фокусным расстоянием собирающей линзы, расстоянием от предмета до линзы и расстоянием от линзы до точки наблюдения изображения, в которой оно будет отчётливым. Чтобы эта формула была применима и для рассевающей линзы, вводят физическую величину оптическая сила линзы.
Поскольку фокус собирающей линзы всегда действительный, а фокус рассеивающей линзы всегда мнимый, оптическую силу определяют так:
Другими словами, оптическая сила линзы равна обратному значению её фокусного расстояния, взятому с «+», если линза собирающая, и взятому с «–», если линза рассеивающая. Единица оптической силы – диоптрия (1 дптр = 1/м). С учётом введённого обозначения получим:
D – оптическая сила линзы, дптр
d – расстояние от предмета до линзы, м
f – расстояние от линзы до изображения, м
Это равенство называют формулой тонкой линзы. Опыты по её проверке показывают, что она справедлива только в том случае, если линза относительно тонкая, то есть её толщина в средней части мала по сравнению с расстояниями d и f. Кроме того, если изображение, даваемое линзой, мнимое, перед величиной f необходимо использовать знак «–».
Задача. Линзу с оптической силой 2,5 дптр поместили на расстоянии 0,5 м от ярко освещённого предмета. На каком расстоянии следует поместить экран, чтобы увидеть на нём чёткое изображение предмета?
Решение. Поскольку оптическая сила линзы положительна, следовательно, линза является собирающей. Определим её фокусное расстояние:
F = 1/D = 1 : 2,5 дптр = 0,4 м, что больше, чем F.
Ответ: экран необходимо поместить на расстоянии 2х метров от линзы. Примечание: задача решена алгебраически, однако мы получим тот же результат и геометрическим путём, приложив к чертежу линейку.
Источник
15
Мар 2012
07 Задание (2022)
Расстояние от линзы до лампочки. Задание 10.
Решение задачи на оптику из Задания 10 из Открытого банка заданий для подготовки к ЕГЭ по математике традиционно вызывают затруднения. Давайте рассмотрим решение такой задачи, и вы поймете, что они решаются совсем просто.
Задание 10 (№ 27970)
Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием 



Решение.
Расстояние от линзы до лампочки – это по условию 

По условию величина 

Посмотрим, при каких условиях правая часть равенства 






Получаем:
Ответ: 36.
Вероятно, Ваш браузер не поддерживается. Попробуйте скачать
Firefox
И.В. Фельдман, репетитор по математике.

Лабораторная
работа № 5
Определение
оптической силы и фокусного расстояния собирающей линзы.
Цель
работы: определить фокусное расстояние и оптическую силу собирающей
линзы.
Оборудование: линейка,
два прямоугольных треугольника, длиннофокусная собирающая линза, лампочка на
подставке с колпачком, содержащим букву, источник тока, ключ, соединительные
провода, экран, направляющая рейка.
Тренировочные
задания и вопросы
- Линзой
называется _____ - Тонкая
линза – это _____ - Покажите
ход лучей после преломления в собирающей линзе.
- Запишите
формулу тонкой линзы. - Оптическая
сила линзы – это _____
D= ______ - Как
изменится фокусное расстояние линзы, если температура ее повысится? - При
каком условии изображение предмета, получаемое с помощью собирающей линзы,
является мнимым? - Источник
света помещен в двойной фокус собирающей линзы, фокусное расстояние
которой F = 2 м. На каком расстоянии от линзы находится
его изображение? - Постройте
изображение в собирающей линзе.
Дайте характеристику полученному
изображению.
Ход
работы
1.
Соберите электрическую цепь, подключив лампочку к источнику тока через
выключатель.
2.
Поставьте лампочку на один край стола, а экран – у другого края. Между ними поместите
собирающую линзу.
3.
Включите лампочку и передвигайте линзу вдоль рейки, пока на экране не будет
получено резкое, уменьшенное изображение светящейся буквы колпачка лампочки.
4.
Измерьте расстояние от экрана до линзы в мм. d=
5.
Измерьте расстояние от линзы до изображения в мм. f
6.
При неизменном d повторите опыт еще 2 раза, каждый раз заново получая резкое
изображение. f, f
7.
Вычислите среднее значение расстояния от изображения до линзы.
f f f= _______
8.
Вычислите оптическую силу линзы D D
9.
Вычислите фокусное расстояние до линзы. F
F=
10.
Результаты вычислений и измерений занесите в таблицу.
|
№ опыта |
f·10¯³, м |
f, м |
d, м |
D, |
D, дптр |
F, м |
11.
Измерьте толщину линзы в мм. h= _____
12.
Вычислите абсолютную погрешность измерения оптической силы линзы по формуле:
∆D = , ∆D = _____
13.
Запишите результат в виде D = D± ∆D D = _____
Вывод:
Компьютерный
эксперимент
1. С помощью данного фокусного
расстояния F, определите оптическую
силу линзы. Внесите данную величину в модель.
2. Для каждого опыта выберите
данные в таблице расстояния от предмета до линзы, выразите эти величины в мм.
3. Для каждого опыта опишите
вид изображения.
4. Результаты этих изображений
занесите в таблицу.
|
№ опыта п/п |
Фокусное расстояние F, см |
Расстояние от предмета до линзы d, см |
Вид изображения |
|
1 |
7 |
3 |
|
|
2 |
7 |
7 |
|
|
3 |
7 |
11 |
|
|
4 |
7 |
14 |
|
|
5 |
7 |
16 |
5. Сформулируйте и запишите вывод
о том, как меняется изображение предмета при его перемещении.
ГОТОВАЯ
РАБОТА УЧАЩЕГОСЯ
Лабораторная
работа № 5
Получение
изображения при помощи линзы.
Цель
работы: научиться получать
различные изображения при помощи собирающей линзы.
Ход
работы
|
№ опыта |
Фокусное |
Расстояние от |
Вид изображения |
|
1 |
7 |
3 |
Прямое, |
|
2 |
7 |
7 |
Изображение |
|
3 |
7 |
11 |
Перевёрнутое, |
|
4 |
7 |
14 |
Равное по |
|
5 |
7 |
16 |
Перевёрнутое, |
=14дптр

1
Вид изображения:
прямое, увеличенное, мнимое.

2.
Вид изображения:
изображение отсутствует.

3
Вид изображения:
перевёрнутое, увеличенное, действительное.
Задание 4.
Вид изображения:
равное по размеру источнику света, перевёрнутое, действительное.
Задание 5
Вид изображения:
перевёрнутое, уменьшенное, действительное.
Вывод:
1) Когда
источник света находится между линзой и ее фокусом его изображение увеличенное,
мнимое и прямое находится с той же стороны линзы что и источник света; по мере
удаления источника света на этом отрезке от линзы, увеличивается его
изображение.
2) Когда источник
света находится в фокусе линзы, его изображение отсутствует.
3) Когда
источник света находится между фокусом и двойным фокусом линзы, его изображение
становится действительным и перевернутым (увеличенным) изображением. Оно
уменьшается по мере приближения источника света к двойному фокусу линзы.
4) Изображение
источника света, находящегося в двойном фокусе линзы, становится изображением,
равным по размеру источнику света, и находится в двойном фокусе линзы по другую
сторону линзы.
5) При увеличении расстояния
от источника света до линзы (d > 2F) изображение источника света
уменьшается, оставаясь действительным и перевернутым, и приближаясь к фокусу
линзы.
Физика 8 класс
Лабораторная работа №11.
Получение изображений при помощи линзы.
Цель: научиться получать различные изображения при помощи собирающей линзы
Оборудование:собирающая линза, экран, лампа с колпачком, в котором сделана прорезь, измерительная лента.
Ход работы
С правилами ТБ ознакомился
1.С помощью линзы получим изображение окна на экране и определим приблизительно фокусное расстояние F линзы.
2. Последовательно располагая лампу на различных расстояниях d от линзы, запишем в таблицу описание получившихся изображений.
Результаты:
| № опыта |
Фокусное Расстояние F, см |
Расстояние от лампы до линзы d, см | Вид изображения |
| Мнимое, увеличенное, прямое | |||
| Действительное, увеличенное, перевернутое | |||
| Действительное, уменьшенное, перевернутое |
3. Постройте изображения и сравните каждое изображение с учебником (стр. 166, рис. 151,152,153).
Сформулируйте вывод о том, как меняется изображение при удалении предмета от линзы.
Вывод:
Свойства тонкой линзы определяются главным образом расположением ее главных фокусов. Поэтому, зная расстояние от источника света до линзы, а также ее фокусное расстояние (положение фокусов), мы можем определить расстояние до изображения, опустив описание хода лучей внутри самой линзы. Поэтому в изображении на чертеже точного вида сферических поверхностей линзы необходимость отсутствует.
Схематически тонкие линзы обозначают отрезком со стрелками на конце. Они смотрят от центра в противоположные стороны, если линза собирающая, и они направлены к центру отрезка, если линза рассеивающая.
Внимание!
Напомним, что линзы могут давать действительные и мнительные изображения. Причем, собирающая линза может давать как действительные, так и мнимые изображения. Рассеивающая линза всегда дает только мнимые изображения.
Способ построения изображений, а также вид самих изображений в линзе зависит от того, где расположен изображаемый предмет. Он может располагаться за двойным фокусным расстоянием, в фокальной плоскости второго фокуса, между вторым и первым фокусом, в фокальной плоскости главного фокуса и на расстоянии меньше фокусного расстояния линзы.
Определение
Вторым фокусом называют точку, которая расположена на главной оптической оси от главного фокуса на расстоянии, равном фокусному расстоянию линзы. Относительно линзы он располагается на расстоянии, равном двойному фокусному расстоянию линзы.
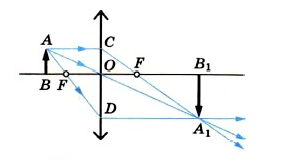
Построение изображения в собирающей линзе
Предметы схематично изображаются в виде стрелки. Чтобы построить изображение предмета в собирающей линзе, нужно найти положение верхней и нижней точки этого изображения. Сначала находят положение точки изображения, соответствующей верхней точки предмета (точки А). Для этого из этой точки нужно пустить два луча:
Два вида лучей при построении изображений в линзе
Первый луч проходит из верхней точки предмета (точки А) параллельно главной оптической оси. На линзе (в точке С) луч преломляется и проходит через точку фокуса (точку F).
Второй луч необходимо направить из верхней точки предмета (точки А) через оптический центр линзы (точку О). Он пройдет, не преломившись.
На пересечении двух лучей обозначаем точку А1. Это и будет изображение верхней точки предмета. Таким же образом нужно поступить с нижней точкой предмета. Но на пересечении вышедших из линзы лучей нужно поставить точку В1. Изображение предмета при этом — А1 В1.
В зависимости от того, где расположен предмет, изображение может получиться действительным или мнимым, увеличенным или уменьшенным, перевернутым или прямым. Построим изображения для каждого из таких случаев.
| Схема построения изображения | Расположение предмета относительно линзы + характеристика изображение |
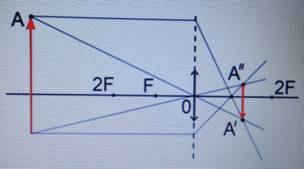 |
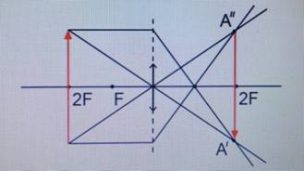
Предмет располагается за двойным фокусом.
Изображение:
|
 |
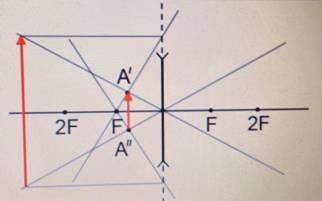
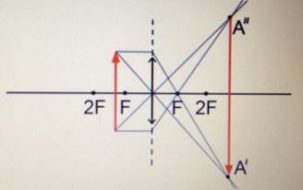
Предмет располагается в фокальной плоскости второго фокуса.
Изображение:
|
 |
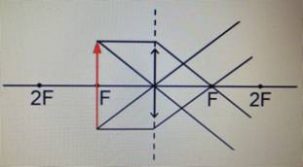
Предмет располагается в пространстве между фокусом и двойным фокусом.
Изображение:
|
 |
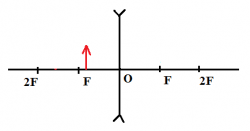
Предмет находится в фокальной плоскости.
Изображения нет, поскольку лучи идут параллельно друг другу и не пересекаются. |
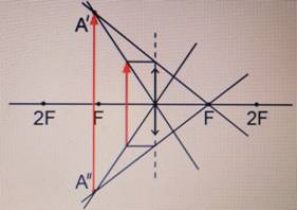 |
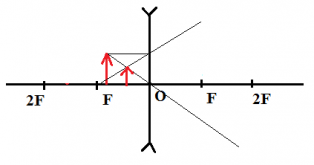
Предмет располагается между линзой и фокусом.
Изображение:
|
Пример №1. Построить изображение предмета, изображенного на рисунке. Определить тип изображения.
Чтобы построить изображение предмета, достаточно определить его положение одной точки — верхней. Поскольку предмет расположен параллельно линзе, для построения изображения, достаточно будет соединить найденную точку изображения для верхней точки предмета перпендикуляром, проведенным к главной оптической оси.
Чтобы построить изображение верхней точки, пустим от нее два луча — побочную оптическую ось через оптический центр и перпендикуляр к линзе. Затем найдем пересечение побочной оптической оси с преломленным лучом. Теперь пустим перпендикуляр к главной оптической оси и получим изображение. Оно является действительным, увеличенным и перевернутым.
Частный случай — построение изображения точки
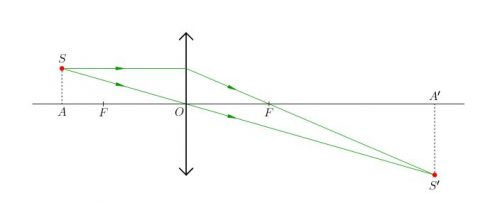
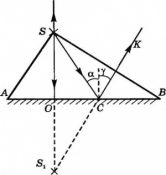
Положение изображения точки можно найти тем же способом, описанным выше. Нужно лишь построить два луча и найти их пересечение после выхода из линзы (см. рисунок ниже). Так, изображению точки S соответствует точка S´.
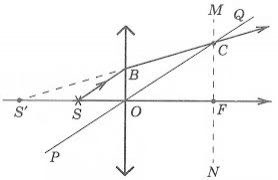
Особую сложность составляет случай, когда точка расположена на главной оптической оси. Сложность заключается в том, что все лучи, которые можно построить, будут совпадать с главной оптической осью. Поэтому возникает необходимость в определении хода произвольного луча. Направим луч от точки S (луч SB) к собирающей линзе. Затем построим побочную оптическую ось PQ такую, которая будет параллельна лучу SB. После этого построим фокальную плоскость и найдем точку пересечения (точка С) фокальной плоскости с побочной оптической осью. Теперь соединим полученную точку С с точкой В. Это будет преломленный луч. Продолжим его до пересечения с главной оптической осью. Точка пересечения с ней и будет изображением точки S. В данном случае оно является мнимым.
Пример №2. Построить изображение точки, расположенной на главной оптической оси.
Чтобы построить изображение, пустим произвольный луч к линзе. Затем построим параллельную ему побочную оптическую ось и фокальную плоскость. Из места пересечения этой оси с фокальной плоскостью пустим луч, также проходящий через точку пересечения линзы с произвольным лучом. Построим продолжение луча до получения точки пересечения с главной оптической осью. Отметим точку пересечения — она является действительным изображением точки.
Построение изображения в рассеивающей линзе
Чтобы построить изображение предмета в рассеивающей линзе, нужно определить положения точек изображения, соответствующих верхней и нижней точкам предмета. Вот как определить положение точки изображения для верхней точки предмета:
- Нужно пустить луч, перпендикулярный главной оптической оси. Этот луч после преломления отклонится. Но его продолжение обязательно пересечет главный фокус линзы.
- Нужно пустить луч от верхней точки предмета через оптический центр линзы (построить побочную оптическую ось).
- Точку пересечения продолжения луча, полученного в шаге 1, с побочной оптической осью, нужно обозначить за изображение верхней точки предмета (на рисунке это точка А´).
Точно такие же действия нужно выполнить для нижней точки предмета. В результате получится точка пересечения, соответствующая изображению нижней точки предмета (на рисунке это точка А´´).
Внимание! Независимо от расположения предмета относительно рассеивающей линзы, изображение всегда получается прямым, уменьшенным, мнимым.
Пример №3. Построить изображение предмета в рассеивающей линзе.
Чтобы построить изображение, пустим от верхней точки предмета побочную оптическую ось через оптический центр и проведем перпендикуляр к линзе. Затем из точки главного фокуса проведем луч через точку пересечения линзы с перпендикуляром. Пересечение этого луча с побочной оптической осью есть изображение верхней точки предмета. Теперь проведем от нее перпендикуляр к главной оптической оси. Это и будет являться изображением предмета. Оно является мнимым, уменьшенным и прямым.
Построение изображений в плоском зеркале
Определение
Плоское зеркало — это плоская поверхность, зеркально отражающая свет.
Построение изображения в зеркалах основывается на законах прямолинейного распространения и отражения света. Продемонстрируем это с помощью рисунка ниже.
Построим изображение точечного источника S. От точечного источника света лучи распространяются во все стороны. На зеркало падает пучок света ASB, и изображение создается всем пучком сразу. Но для построения изображения достаточно взять любые два луча из этого пучка. Пусть это будут лучи SO и SC. Луч SO падает перпендикулярно поверхности зеркала АВ. Поскольку угол между ним и перпендикуляром, восстановленным в точке падения, равен 0, то угол падения принимаем равным за 0. поэтому отраженный пойдет в обратном направлении OS. Луч SC отразится под углом γ=α. Отраженные лучи OS и СК расходятся и не пересекаются, но если они попадают в глаз человека, то человек увидит изображение S1, которое представляет собой точку пересечения продолжения отраженных лучей.
Таким образом, чтобы получить изображение в плоском зеркале, нужно:
- Пустить от источника света луч, перпендикулярный к плоскости зеркала (падающий луч совпадает с отраженным лучом).
- Пустить от источника света к плоскости зеркала еще один луч под произвольным углом.
- Построить отраженный луч от падающего луча, построенного в шаге 2, используя закон отражения света.
- Найти пересечение продолжений отраженных от зеркала лучей (пущенного под прямым углом и произвольным углом).
Внимание!
Изображение в зеркале всегда является мнимым. Это связано с тем, что изображение строится на пересечении продолжении лучей, а не на самих лучах.
Изображение в плоском зеркале находится от зеркала на таком же расстоянии, как предмет от этого зеркала. Это легко доказать тем, что треугольники SOC и S1OC равны по стороне и двум углам. Следовательно SO = S1O. Отсюда делаем вывод, что для построения изображения точечного источника света достаточно знать расстояние, на котором он находится от зеркала. Останется только провести к зеркалу перпендикулярную прямую и отложить на ней точку на нужном расстоянии.
При построении изображения какого-либо предмета последний представляют как совокупность точечных источников света. Поэтому достаточно найти изображение крайних точек предмета. Так, изображение А1В1 соответствует предмету АВ.
Изображение и сам предмет всегда симметричны относительно зеркала.
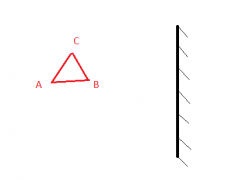
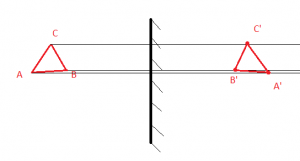
Пример №4. Построить изображение треугольника ABC в плоском зеркале.
Чтобы построить изображение, пустим к плоскому зеркалу перпендикулярные прямые. Затем измерим расстояние от каждой точки до зеркала и отложим их по перпендикуляру от зеркала в обратную сторону. Так для точки А мы находим точку А´, для В — В´, для С — С´.
Видно, что треугольник отразился зеркально (изображение и предмет симметричны друг другу). Так и должно быть в случае с зеркалом.
Задание EF17760

Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Сделать рисунок — построить изображение в линзе.
3.Записать формулу для нахождения площади полученной фигуры.
4.Выполнить решение в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Оптическая сила линзы: D = 2,5 дптр.
• Сторона треугольника AC = 4 см.
4 см = 0,04 м
Построим изображение в линзе. Для этого достаточно построить изображение точки В. Сначала пустим луч, параллельный главной оптической оси, к плоскости линзы. Он будет преломляться, после чего пройдет через фокус. Затем пустим луч через оптический центр. На месте пересечения двух лучей поставим точку и обозначим ее за B´.
Так как точки B и C предмета лежат на одной прямой, перпендикулярной главной оптической оси, для нахождения точки изображения C´ достаточно пустить перпендикуляр от B´ этой оси. На месте пересечения поставим точку и обозначим ее C´.
Рассматривать ход лучей для построения точки A´ тоже не будем. Точка A лежит в плоскости второго фокуса. Значит, она будет находиться в этой же точке и с противоположной стороны линзы. Это легко доказать с помощью формулы тонкой линзы:
1d+1f=1F
Если расстояние от предмета до линзы равно 2F, то и расстояние от линзы до его изображения будет 2F:
12F+1f=1F
1f=1F−12F=2−12F=12F
f=2F
Теперь соединим все найденные точки и получим треугольник A´ B´ C´. Найдем его площадь. Поскольку это прямоугольный треугольник, его площадь будет равна половине произведения двух катетов — B´ C´и A´ C´:
S=A´C´·B´C´2
Из формулы оптической силы линзы найдем фокусное расстояние:
F=1D=12,5=0,4 (м)
Известно, что точка A находится в точке двойного фокусного расстояния. И ее изображение тоже находится на таком же расстоянии от линзы. Следовательно, чтобы найти длину катета A´ C´, нужно найти расстояние от точки C до ее изображения. Расстояние от этой точки до линзы равно разности двойного фокусного расстояния и длины отрезка AC:
dC=2F−AC=2·0,4−0,04=0,76 (м)
Используя формулу тонкой линзы, вычислим расстояние от линзы до изображения этой точки:
10,76+1f=1F
1fC=1F−10,76=0,76−F0,76F=0,76−0,40,76·0,4
fC=0,76·0,40,76−0,4=0,844 (м)
Тогда длина катета A´ C´ будет равна:
A´C´=fC−fA=fC−2F=0,844−0,4·2=0,044 (м)
Треугольники BCO и B´ C´O подобны по 3 углам. Углы O равны как вертикальные. Углы C и C´ как прямые, а B и B´ как накрест лежащие (полученные при пересечении секущей в виде луча через оптический центр и параллельных фокальных плоскостей). Следовательно BC относится к B´ C´ так же, как OC относится к C´O:
BCB´C´=ACA´C´
Треугольник ABC равнобедренный, поэтому BC = AС. Тогда:
ACB´C´=ACA´C´
Следовательно:
B´C´=A´C´
Отсюда площадь треугольника равна:
S=A´C´·A´C´2=(0,044)22=0,000968 (м2)=9,68 (см2)
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18181
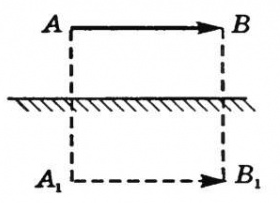
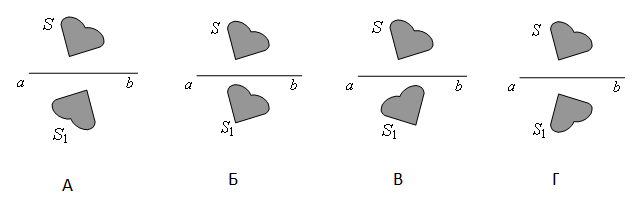
Предмет S отражается в плоском зеркале ab. На каком рисунке верно показано изображение S1 этого предмета?
Ответ:
Алгоритм решения
- Записать, какое изображение дает плоское зеркало.
- Выбрать изображение, которое соответствует типу описанного изображения.
Решение
Зеркало дает мнимое изображение предмета без увеличения в зеркальном отражении. Это значит, что предмет и его изображение должны быть симметричны относительно плоскости зеркала. Симметричными являются только предмет и его изображение на последнем рисунке — Г.
Ответ: Г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18876
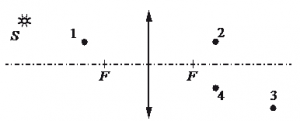
Алгоритм решения
1.Построить изображение точки.
Решение
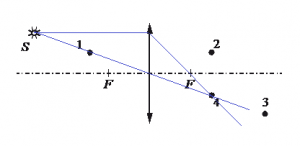
Построим изображение точки с учетом того, что линза собирающая. Для этого пустим из этой точки луч света, параллельный главной оптической оси. После прохождения через линзу луч преломится и пройдет через фокус. Затем пустим луч от этой точки через оптический центр линзы. Точка, в которой оба луча пересекутся, будет искомой. В данном случае это точка 4.
Ответ: 4
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 32.3k