

ГДЗ (готовое домашние задание из решебника) на Номер №530 по учебнику Геометрия. 10-11 классы: учебник для общеобразовательных учреждений : базовый и профильный уровни / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 22-е изд. – Просвещение, 2013-2019г
Условие
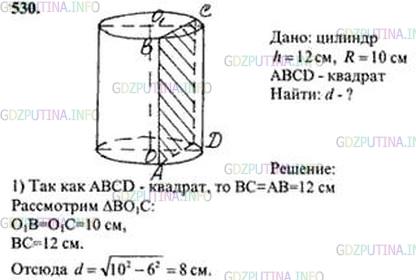
Высота цилиндра равна 12 см, а радиус основания равен 10 см. Цилиндр пересечен плоскостью, параллельной его оси, так, что в сечении получился квадрат. Найдите расстояние от оси цилиндра до секущей плоскости.
Решение 1

Решение 2
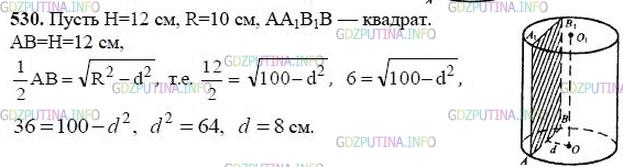
Решение 3
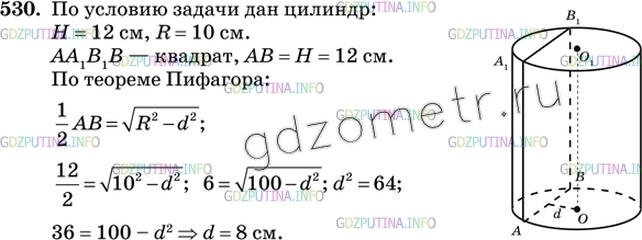
Решение 4
Популярные решебники
Ваше сообщение отправлено
и скоро будет рассмотрено
Задача №1.
на проекции видно, что треугольник АОВ – равнобедренный ОА = ОВ =R =10 см
основание треугольника АВ= 12 см (это сторона квадратного сечения – она равна высоте h= 12 см)
расстояние от оси цилиндра до секущей плоскости – высота d
высота d делит сторону АВ на равные части , тогда АК=АВ/2=12/2= 6 см
тогда по теореме Пифагора
d^2 = OA^2 – AK^2= R^2 – AK^2 = 10^2 – 6^2 = 64= 8^2
d= 8 см
Ответ 8 см расстояние от оси цилиндра до секущей плоскости.
Задача №2
Из правил сервиса: “Пользователи признают, что задания, которые содержат большое количество задач, требующих решения, должны быть разделены на два или несколько заданий и в таком виде добавлены в Сервис для других Пользователей. То есть в одном задании не может быть несколько задач”.
-
ГДЗ
-
10 класс
-
Геометрия
-
Атанасян 10-11
-
530
Подробное решение задача № 530 по геометрии для учащихся 10 класса, авторов Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. 2015
показать содержание
← предыдущее
Следующее →
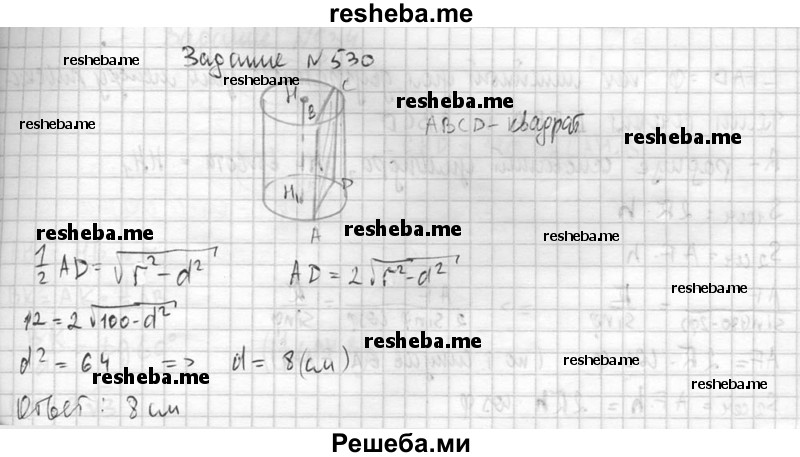
530. Высота цилиндра равна 12 см, а радиус основания равен 10 см. Цилиндр пересечен плоскостью, параллельной его оси, так, что в сечении получился квадрат. Найдите расстояние от оси цилиндра до секущей плоскости.
Решебник №2 / задача № / 530

← предыдущее
Следующее →
Подпишись на нашу группу
×
© 2023 «Resheba.me»
Хостинг для сайта от 113,5 руб/мес.
[email protected]
Разные окружности оснований в цилиндре
Отрезок АВ равен 13 см, точки А и В лежат на разных окружностях оснований цилиндра. Найдите расстояние от отрезка АВ до оси цилиндра, если его высота равна 5 см, а радиус основания равен 10 см.
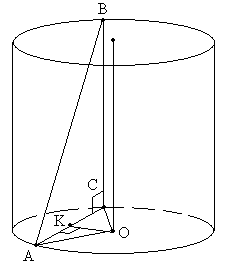
Мы видим, что АВ и ось цилиндра – скрещивающиеся прямые.
Все о скрещивающихся прямых тут, в том числе и способ и принцип нахождения расстояния между скрещивающимися прямыми.
Используя правила нахождения расстояния между ск. прямыми (которые смотрим по ссылке выше) найдем отрезок ОК являющийся расстоянием между нашими ск. прямыми АВ и осью цилиндра.
Рассмотрим треугольник АВС: в нем АВ = 13, ВС равно высоте цилиндра = 5 и он прямоугольный по построению (подробнее о прямоугольных треугольниках тут). Поэтому по теореме Пифагора находим АС = 12.
Рассмотрим треугольник ОАС: он равнобедренный ОА=ОС – радиусы основания и в нем ОК – высота опущенная на основание. Она делит основание попалам АК=КС=6.
Рассмотрим треугольник АКО: он прямоугольный и в нем АК = 6 и ОА = 10 – радиус основания цилиндра. Поэтому по теореме Пифагора определяем ОК = 8
Отрезок CD 25 см, его концы лежат на разных окружностях оснований цилиндра?
Геометрия | 10 – 11 классы
Отрезок CD 25 см, его концы лежат на разных окружностях оснований цилиндра.
Найдите расстояние от отрезка CD до оси цилиндра, если его высота 7см а диаметр основания 26 см.

Опустим из точки D перпендикуляр DH на основание цилиндра.
DH равен высоте цилиндра.
Тогда хорда СН по Пифагору равна √(CD² – DH²) = √(25² – 7²) = 24см.
Проведем диаметр АВ параллельно хорде СН.
Тогда перпендикуляр ОК и будет искомым расстоянием от отрезка CD до оси цилиндра, так как этот перпендикуляр является расстоянием между двумя параллельными плоскостями СDH (содержащую отрезок CD) и АА’BB’ (содержащую ось цилиндра).
Отрезок ОК делит хорду СН пополам.
Тогда по Пифагору
ОК = √(ОС² – СК²) = √(13² – 12²) = 5см.
Ответ : расстояние от отрезка CD до оси цилиндра равно 5см.


Концы отрезка АВ лежат на окружностях оснований цилиндра?
Концы отрезка АВ лежат на окружностях оснований цилиндра.
Радиус цилиндра равен 5 ддм, а расстояние между прямой АВ и осью цилиндра равно 4 дм, АВ = 10.

Высота цилиндра равна 15 см , радиус основания 10 см?
Высота цилиндра равна 15 см , радиус основания 10 см.
Дан отрезок , концы которого принадлежат окружностям обоих оснований и длина которого равна 3 корня из 41 см .
Найдите расстояние между данным отрезком и осью цилиндра.
Нарисуйте рисунок пожалуйста!

Диаметр основания цилиндра равен 1 м высота цилиндра равна длине окружности основания?
Диаметр основания цилиндра равен 1 м высота цилиндра равна длине окружности основания.
Найдите площадь боковой поверхности цилиндра.

Концы отрезка AB лежат на разных основаниях цилиндра?
Концы отрезка AB лежат на разных основаниях цилиндра.
Радиус цилиндра равен r, его высота h, расстояние между прямой AB и осью цилиндра равно D.
Найдите высоту, если r = 12, d = 5, AB = 15.
С решением по действиям!

Концы отрезка АВ лежат на окружностях оснований цилиндра?
Концы отрезка АВ лежат на окружностях оснований цилиндра.
Радиус основания равен 5 см, высота цилиндра равна 6 см, АВ = 10 см.
Определите расстояние между прямой АВ и осью цилиндра.

Отрезок CD концы которого лежат на разных окружностях оснований цилиндра, пересекает ось цилиндра под углом 60 градусов?
Отрезок CD концы которого лежат на разных окружностях оснований цилиндра, пересекает ось цилиндра под углом 60 градусов.
Найдите объём цилиндра, если длина отрезка CD равна 8 см.

Найдите площадь сечения цилиндра, проведенного паралельно оси на расстояниии 3 см от оси, если высота цилиндра 13 см, а радиус основания цилиндра равен 5 см?
Найдите площадь сечения цилиндра, проведенного паралельно оси на расстояниии 3 см от оси, если высота цилиндра 13 см, а радиус основания цилиндра равен 5 см.

На окружностях обоих оснований цилиндра выбрано по точке, расстояние между которыми равно 13?
На окружностях обоих оснований цилиндра выбрано по точке, расстояние между которыми равно 13.
Найдите расстояние от этого отрезка до оси цилиндра , если высота цилиндра равна 5 , а радиус основания равен 10.

Диаметр основания цилиндра равен 1 метр, высота цилиндра равна длине окружности основания?
Диаметр основания цилиндра равен 1 метр, высота цилиндра равна длине окружности основания.
Найдите площадь боковой поверхности цилиндра.

1) Высота цилиндра 8см, диаметр основания 10 см?
1) Высота цилиндра 8см, диаметр основания 10 см.
Найдите площадь сечения , проведенного параллельно оси цилиндра на расстоянии 4 см.
Вы зашли на страницу вопроса Отрезок CD 25 см, его концы лежат на разных окружностях оснований цилиндра?, который относится к категории Геометрия. По уровню сложности вопрос соответствует учебной программе для учащихся 10 – 11 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.

Площадь трапеции есть произведение полусуммы оснований на высоту. S = (15 + 19)×h / 2 ; S = (15 + 19) * 18 / 2 = 34 * 18 / 2 = 34 * 9 = 306.

Я сфотографувала правильну відповідь.

Если в словаре то все по алфавиту. То есть последние буквы Э Ю Я. Ну думая на Я. Ответ : на Я.

В прямоугольном треугольнике АВС с b² = 196. B = 14. Ответ : катет, расположенный против угла 60°, равен 14 ед.

У параллелограмма противоположные стороны равны и параллельны Если у четырехугольника противоположные стороны равны и параллельны то это параллелограмм если суммы противоположных сторон четырехугольника равны, то в такой четырехугольник можно вписать..

Например теорема Виета и теорема обратная теореме Виета.

Применены : свойства правильной четырёхугольной усеченной пирамиды, теорема Пифагора.

Нет, так как AC меньше BC.

У равнобедренного треугольника нет гипотенузы.

Треугольник FES = треугольникуSED по третьему признаку значит угол FES = углу SED и они равны по 45°. Угол FSE равен углу DSE и они равны по 90°. Угол SDE равен углу SFE и равны они по 45°.
Что такое цилиндр: определение, элементы, виды, варианты сечения
В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения одной из самых распространенных трехмерных геометрических фигур – цилиндра. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.
Определение цилиндра
Далее мы подробно остановимся на прямом круговом цилиндре как самой популярной разновидности фигуры. Другие ее виды будут перечислены в последнем разделе данной публикации.
Прямой круговой цилиндр – это геометрическая фигура в пространстве, полученная путем вращения прямоугольника вокруг своей стороны или оси симметрии. Поэтому такой цилиндр иногда называют цилиндром вращения.

Цилиндр на рисунке выше получен в результате вращения прямоугольного треугольника ABCD вокруг оси O1O2 на 180° или прямоугольников ABO2O1/O1O2CD вокруг стороны O1O2 на 360°.
Основные элементы цилиндра
- Основания цилиндра – два одинаковых по размеру/площади круга с центрами в точках O1 и O2.
- R – радиус оснований цилиндра, отрезки AD и BC – диаметры (d).
- O1O2 – ось симметрии цилиндра, одновременно является его высотой (h).
- l (AB, CD) – образующие цилиндра и одновременно с этим стороны прямоугольника ABCD. Равны высоте фигуры.
Развёртка цилиндра – боковая (цилиндрическая) поверхность фигуры, развернутая в плоскость; является прямоугольником.

- длина данного прямоугольника равна длине окружности основания цилиндра ( 2πR );
- ширина равна высоте/образующей цилиндра.
Примечание: формулы для нахождения площади поверхности и объема цилиндра представлены в отдельных публикациях.
[spoiler title=”источники:”]
http://geometria.my-dict.ru/q/2038569_otrezok-cd-25-sm-ego-koncy/
[/spoiler]
oulor
Вопрос по геометрии:
Высота цилиндра 16 см, радиус основания 10 см. Цилиндр пересечен плоскостью параллельно оси так, что в сечении получается квадрат. Найдите расстояние от оси цилиндра до этого сечения.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 1
ldremoumat
h =16 см
R =10 см
По условию задачи – в сечении получается квадрат.
Значит площадь сечения S =a*h
a – хорда окружности основания, через которую проходит сечение
h – высота цилиндра
если сечение квадрат, значит a=h =16 см
расстояние от оси цилиндра до этого сечения
b =√ ( R^2 – (a/2)^2) = √ ( 10^2 – (16/2)^2) = 6 см
ответ 6 см
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

