Расстояния в пространстве

§ 18.Расстояние от точки до фигуры
Мы уже говорили о расстоянии между двумя точками (рис. 113).
Расстояние от точки M до фигуры F мы будем обозначать: ρ (M; F) Это обозначение не является общепринятым, но, как нам кажется, очень удобно. .
Если точка M принадлежит фигуре F, то расстояние от неё до фигуры F равно нулю. Например, расстояние от любой вершины куба до этого куба равно нулю.
Если точка M не принадлежит фигуре F, то рассматриваются всевозможные расстояния от данной точки до каждой точки фигуры F. Наименьшее из них и принимается за расстояние от точки M до фигуры F.
Таким образом: если точка M не принадлежит фигуре F и существует принадлежащая фигуре F точка A такая, что | MA| ⩽ |MX | для любой точки X фигуры F, то длина отрезка MA называется расстоянием от точки M до фигуры F, а точка A — ближайшей к точке M точкой фигуры F. При этом пишут: ρ (M; F) = | MA | (рис. 114).

Рис. 113

Рис. 114

Рис. 115
Заметим, что такое определение расстояния от точки до фигуры применимо как на плоскости, так и в пространстве. Более того, если точка M и фигура F лежат в одной плоскости (F — плоская фигура), то расстояние ρ(M; F) на плоскости будет таким же, как и в пространстве.
Рассмотрим расстояния от различных точек пространства до сферы S с центром O радиуса R.
Если точка M расположена вне шара с центром O и радиусом R (т. е. | OM | > R), то точка A пересечения отрезка OM со сферой S является ближайшей к M точкой этой сферы (что нетрудно показать при помощи неравенства треугольника) (рис. 115). Таким образом, ρ(M; S) = | MA | = | MO | – R.
Если точка M1 расположена внутри шара (рис. 115), но не совпадает с его центром (т. е. 0 < | OM1 | < R), то точка A1 пересечения луча OM1 со сферой является ближайшей к M1 точкой сферы, т. е. ρ (M1; S) = R – | OM1|.
Если точка M лежит на сфере, то ρ(M; S) = 0.
Если, наконец, точка M является центром сферы, то любая точка сферы является ближайшей к точке M и ρ(M; S) = R.
 В данной фигуре F может не быть точек, ближайших к данной точке М. Такая ситуация может быть, например, в случае, когда фигура F — множество всех внутренних точек шара с центром О и радиусом, равным 1 (т. е. всех таких точек X, для которых 0 ⩽ | OX| < 1). Такое множество точек называют открытым шаром (шар без ограничивающей его сферы). Если при этом точка М удалена от центра О шара на расстояние, равное 5, то в открытом шаре нет точки, ближайшей к точке М: на отрезке МО не существует такой точки X, принадлежащей данному шару, для которой длина отрезка MX достигает своего минимума. Поэтому введённое выше определение расстояния от точки до замкнутой фигуры не распространяется для определения расстояния от данной точки до открытого множества точек («открытой» фигуры). В курсе школьной геометрии рассматриваются, вообще говоря, замкнутые фигуры: шар с ограничивающей его сферой — поверхностью шара, которую называют шаровой поверхностью; многогранник — геометрическое тело, границей (поверхностью) которого является объединение конечного числа многоугольников — многогранная поверхность. Об этом речь пойдёт в курсе стереометрии 11 класса.
В данной фигуре F может не быть точек, ближайших к данной точке М. Такая ситуация может быть, например, в случае, когда фигура F — множество всех внутренних точек шара с центром О и радиусом, равным 1 (т. е. всех таких точек X, для которых 0 ⩽ | OX| < 1). Такое множество точек называют открытым шаром (шар без ограничивающей его сферы). Если при этом точка М удалена от центра О шара на расстояние, равное 5, то в открытом шаре нет точки, ближайшей к точке М: на отрезке МО не существует такой точки X, принадлежащей данному шару, для которой длина отрезка MX достигает своего минимума. Поэтому введённое выше определение расстояния от точки до замкнутой фигуры не распространяется для определения расстояния от данной точки до открытого множества точек («открытой» фигуры). В курсе школьной геометрии рассматриваются, вообще говоря, замкнутые фигуры: шар с ограничивающей его сферой — поверхностью шара, которую называют шаровой поверхностью; многогранник — геометрическое тело, границей (поверхностью) которого является объединение конечного числа многоугольников — многогранная поверхность. Об этом речь пойдёт в курсе стереометрии 11 класса. 

Рис. 116

Рис. 117
Расстоянием от данной точки M до данной прямой a, не проходящей через точку M, является длина перпендикуляра, опущенного из точки M на прямую a (рис. 116); основание этого перпендикуляра есть ближайшая к M точка прямой a.
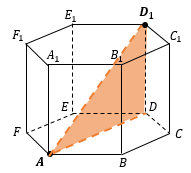
Рассмотрим, к примеру, правильный тетраэдр ABCD с длиной ребра a, в котором точка M — середина ребра AB. Найдём расстояния от этой точки до прямых, содержащих рёбра тетраэдра (рис. 117). Получаем:
ρ(M; AB) = 0, так как точка M лежит на прямой AB;
расстояния от точки M до прямых AC, BC, BD, AD равны  , а ближайшей к M точкой, например, ребра BC является точка HBC, делящая это ребро в отношении BH : HC = 1 : 3;
, а ближайшей к M точкой, например, ребра BC является точка HBC, делящая это ребро в отношении BH : HC = 1 : 3;

Рис. 118

Рис. 119
так как треугольник MDC — равнобедренный (почему?), то нетрудно показать, что расстояние от точки M до прямой DC равно длине отрезка MK, где точка K — середина DC — является ближайшей к M точкой прямой CD. Поэтому ρ(M; DC) = | MK | =  .
.
Расстоянием от точки M до плоскости α, не проходящей через эту точку, является длина перпендикуляра MA, опущенного из данной точки M на плоскость (рис. 118), а основание A этого перпендикуляра есть ближайшая к M точка плоскости α (это утверждение становится очевидным, если вспомнить о сравнении длин перпендикуляра и наклонной) (рис. 119).
Заметим, что если прямая a параллельна плоскости α, то расстояние между ними равно расстоянию от любой точки прямой a до плоскости α, так как это расстояние для любой точки прямой a одно и то же (рис. 120).
Далее, если две плоскости параллельны, то расстояние между ними равно расстоянию от любой точки одной из данных плоскостей до другой, так как расстояния от любой точки одной из этих плоскостей до другой плоскости одинаковы (рис. 121).

Рис. 120

Рис. 121
Докажите самостоятельно одно часто используемое при решении задач соотношение: пусть точки A и B не лежат в плоскости α, а прямая AB пересекает эту плоскость в точке O, тогда  =
=  (рис. 122).
(рис. 122).

Рис. 122

Рис. 123
В качестве примера рассмотрим решение следующей задачи.
ЗадаЧа 1. Пусть MABCD — правильная четырёхугольная пирамида (рис. 123). Расстояние от точки O пересечения диагоналей квадрата ABCD до плоскости MBC равно 1. Требуется найти расстояние до плоскости MBC от: а) вершины D; б) точки K пересечения медиан треугольника MAD; в) точки F пересечения медиан треугольника MDC.
Решение. а) Так как точка O является серединой отрезка BD, то
 =
=  = 2.
= 2.
Следовательно, ρ(D; (MBC)) = 2.
б) Пусть N — середина AD, H — середина BC. Тогда ρ(N; (MBC)) = 2, так как точка O — середина NH и ρ(O; (MBC)) = 1.
Далее, прямая NK пересекает плоскость MBC в точке M и  =
=  . Значит,
. Значит,  =
=  =
=  .
.
Тогда ρ(K; (MBC)) =  .
.
в) Если DF пересекает MC (а следовательно, и плоскость (MBC)) в точке Q, то  =
=  =
=  . А так как ρ(D; (MBC)) = 2, то ρ(F; (MBC)) =
. А так как ρ(D; (MBC)) = 2, то ρ(F; (MBC)) =  .
.

Рис. 124
Отметим, что приведённый метод нахождения расстояния от точки до плоскости позволяет решать подобного рода задачи без построения на рисунках тех перпендикуляров, длины которых равны искомым расстояниям от точек до соответствующих плоскостей. (На рис. 123 перпендикуляры проведены для наглядности предложенного метода. Для решения задачи достаточно найти на рисунке подобные треугольники.)
Многие задачи на нахождение расстояний в пространстве состоят в нахождении расстояния от некоторой точки M, не лежащей в плоскости α, до фигуры F, лежащей в этой плоскости. Для решения задач такого рода удобно применять следующий приём.
Опустим из точки M на плоскость α перпендикуляр MH. Его длина | MH| = h есть расстояние от точки M до плоскости α (рис. 124).
Если точка H принадлежит фигуре F, то расстояние от точки M до фигуры F равно h.
Если же точка H не принадлежит фигуре F, то мы находим на фигуре F точку A, ближайшую к H. Тогда расстояние от точки M до фигуры F равно длине отрезка AM, т. е.
| AM |2 = ρ2(M; F) = ρ2(M; α) + ρ2(H; F).
Действительно, так как A — точка фигуры F, ближайшая к точке H, то | HA | ⩽ | HN | для любой точки N фигуры F. После применения теоремы Пифагора к прямоугольным треугольникам AMH и NMH получаем соответственно | MA |2 = ρ2(M; α) + | HA |2 и | MN |2 = ρ2(M; α) + HN2, откуда (с учётом | HA | ⩽ | HN |) следует | MA |2 ⩽ | MN |2, т. е. | MA | ⩽ | MN |.
Используя соотношение ρ2(M; F) = ρ2(M; α) + ρ2(H; F), попробуйте придумать новое доказательство теоремы о трёх перпендикулярах.
Для иллюстрации сказанного выше рассмотрим решение задачи.

Рис. 125
ЗадаЧа 2. Из вершины A трапеции ABCD (AB = BC = CD = a; AD = 2a) к её плоскости проведён перпендикуляр AM, длина которого равна a. Найти расстояния от точки M до прямых, содержащих стороны и диагонали данной трапеции (рис. 125, а, б).
Решение. Расстояния от точки M до прямых AB, AC и AD равны a, так как эти прямые содержат точку A — основание перпендикуляра, опущенного из точки M на плоскость трапеции.
Так как расстояние от точки A до прямой BC равно высоте трапеции и равно  , то расстояние от M до прямой BC равно
, то расстояние от M до прямой BC равно  =
=  .
.
Расстояние от точки A до прямой DC равно длине диагонали AC (треугольник ACD — прямоугольный) и равно  , следовательно, расстояние от точки M до прямой DC равно
, следовательно, расстояние от точки M до прямой DC равно  = 2a.
= 2a.
Расстояние от точки A до прямой BD равно длине отрезка AB (треугольник ABD — прямоугольный), следовательно, расстояние от точки M до прямой BD равно  .
.

Рис. 126
При решении задач на нахождение угла между прямой и плоскостью полезно пользоваться следующим приёмом.
Пусть расстояние от точки A до плоскости α равно h, а точка O лежит в плоскости α. Тогда синус угла ϕ между прямой OA и плоскостью α равен  sin ϕ =
sin ϕ =  (рис. 126)
(рис. 126) .
.

Рис. 127
Есть удобное соотношение и для нахождения угла φ между двумя пересекающимися плоскостями α и β. Именно, если точка A лежит в плоскости α, а расстояния от неё до плоскости β и до прямой пересечения данных плоскостей равны соответственно h и m, то синус угла между плоскостями α и β равен  sin ϕ =
sin ϕ =  (рис. 127).
(рис. 127).
Расстояния
Задача на нахождения расстояния в стереометрической фигуре является главной и самой важной из всех. Прежде всего определимся с тем, что имеется ввиду под словом «расстояние», ведь их может быть бесконечно много.
Расстояние между объектами в геометрии – это кратчайшее из расстояний между ними.
Обозначение:

В стереометрии найти расстояние можно между следующими комбинациями фигур:
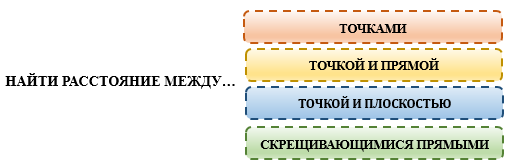
РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ
Расстояние между точками– это длина отрезка, соединяющего эти точки.
В задачах на стереометрию мы не можем просто воспользоваться линейкой, и длину этого отрезка должны найти аналитически. Поэтому длину отрезка AB между точками A и B находят как сторону треугольника, если отрезок AB удается включить в некоторый треугольник в качестве одной из его сторон.
То есть если в задаче предлагается найти расстояние между точками, нужно задать себе вопрос: «В каком треугольнике этот отрезок является стороной?», затем построить этот треугольник и найти в нем нужную сторону.
Например:

|
|
|
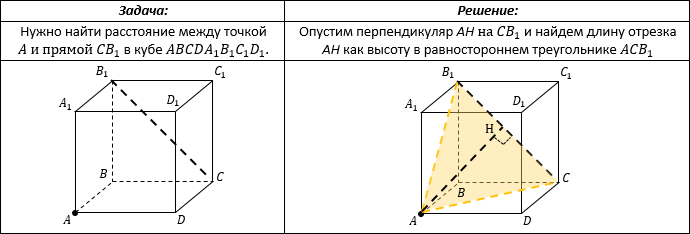
РАССТОЯНИЕ МЕЖДУ ТОЧКОЙ И ПРЯМОЙ
Расстояние от точки до прямой – длина перпендикуляра, опущенного из точки на прямую.

Этот отрезок перпендикуляра можно вычислить, включив его в треугольник (или трапецию) в качестве одной из высот. То есть нужно задать себе вопрос: «В каком треугольнике этот отрезок является высотой?», затем построить этот треугольник и найти в нем высоту.
Например:
РАССТОЯНИЕ МЕЖДУ ТОЧКОЙ И ПЛОСКОСТЬЮ
Существует несколько способов нахождения расстояния от точки до плоскости:
- Построение перпендикуляра из точки на плоскость.
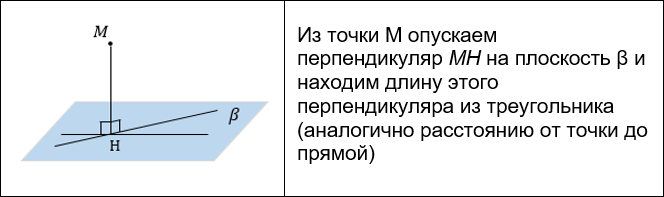
- К этому способу обращаются, если расстояние из точки M на плоскость опускать неудобно, а удобно опустить равный ему перпендикуляр из другой точки, лежащей на одной линии с M.
- Построение перпендикуляра из точки прямой к плоскости.
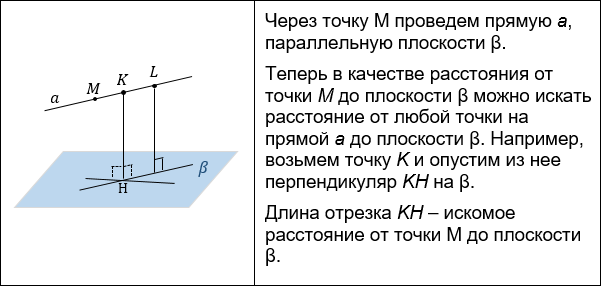
- Построение перпендикуляра из точки плоскости на плоскость.
К этому способу, аналогично, обращаются, если расстояние из точки M на плоскость опускать неудобно, а удобно опустить равный ему перпендикуляр из другой точки, лежащей на одной плоскости с M.

- Через двойное выражение объема.
Расстояние от точки M до плоскости β – это перпендикуляр, опущенный из точки на плоскость, то есть по сути это высота в некоторой пирамиде с вершиной M и плоскостью основания, лежащей на β. Если легко вычислить объем этой пирамиды, используя другое основание и другую высоту, то через этот объем можно найти нужное расстояние.
Например:

РАССТОЯНИЕ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ
Существует несколько способов нахождения расстояния между скрещивающимися прямыми:
1. Построение взаимного перпендикуляра.

2. Построение параллельной прямой.
К этому способу обращаются, если строить взаимный перпендикуляр неудобно и одна из скрещивающихся прямых уже заключена в удобную плоскость.
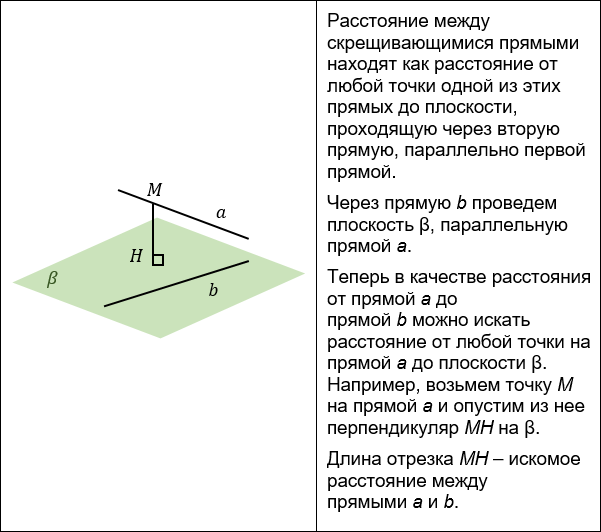 К этому способу обращаются, если строить взаимный перпендикуляр неудобно и скрещивающиеся прямые уже заключены в удобные плоскости.
К этому способу обращаются, если строить взаимный перпендикуляр неудобно и скрещивающиеся прямые уже заключены в удобные плоскости.
3. Построение параллельной плоскости.

Назовите кто − нибудь
Нам синоним к слову «путь»!

Назовите кто − нибудь
Нам синоним к слову «путь»!
Без труда его найдёте
Вы от точки до другой,

Назовите кто − нибудь
Нам синоним к слову «путь»!
Без труда его найдёте
Вы от точки до другой,
А потом определите
И от точки до прямой.

РАССТОЯНИЕ

РАССТОЯНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ

Как найти расстояние между палатками?
РАССТОЯНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ

РАССТОЯНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ
Расстояние между палатками – это длина отрезка,
который соединяет эти палатки.

РАССТОЯНИЕ ОТ ТОЧКИ ДО ФИГУРЫ

Расстояние − это всегда длина кратчайшего пути.
РАССТОЯНИЕ ОТ ТОЧКИ ДО ФИГУРЫ

РАССТОЯНИЕ ОТ ТОЧКИ ДО ФИГУРЫ
Как проложить кратчайший путь от дома лесника до озера?

Будем проводить окружности с центром в точке А, увеличивая их радиусы, пока одна из них «не достигнет” озера.
РАССТОЯНИЕ ОТ ТОЧКИ ДО ФИГУРЫ

Будем проводить окружности с центром в точке А, увеличивая их радиусы, пока одна из них «не достигнет” озера.
РАССТОЯНИЕ ОТ ТОЧКИ ДО ФИГУРЫ

В результате найдём точку озера, ближайшую к дому лесника.
РАССТОЯНИЕ ОТ ТОЧКИ ДО ФИГУРЫ

Длина отрезка АМ и есть расстояние от дома лесника до озера.
РАССТОЯНИЕ ОТ ТОЧКИ ДО ФИГУРЫ

РАССТОЯНИЕ ОТ ТОЧКИ ДО ФИГУРЫ
Как найти расстояние от дома лесника до шоссе,
которое проходит по прямой?

РАССТОЯНИЕ ОТ ТОЧКИ ДО ФИГУРЫ
Расстояние от дома лесника до шоссе – длина перпендикуляра, проведенного из точки А к шоссе, которое проходит по прямой.

ЗАДАЧИ НА ПОСТРОЕНИЕ

РАССТОЯНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ
Нахождение расстояния между двумя точками.

РАССТОЯНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ
Нахождение расстояния между двумя точками.

РАССТОЯНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ
Нахождение расстояния между двумя точками.

РАССТОЯНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ
Нахождение расстояния между двумя точками.

РАССТОЯНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ
АВ = 13 см
Расстояние между точками А и В − длина отрезка АВ.

РАССТОЯНИЕ ОТ ТОЧКИ ДО ФИГУРЫ
Нахождение расстояния от точки до прямой.

Нахождение расстояния от точки до прямой.
РАССТОЯНИЕ ОТ ТОЧКИ ДО ФИГУРЫ

Нахождение расстояния от точки до прямой.
РАССТОЯНИЕ ОТ ТОЧКИ ДО ФИГУРЫ

Нахождение расстояния от точки до прямой.
РАССТОЯНИЕ ОТ ТОЧКИ ДО ФИГУРЫ

Нахождение расстояния от точки до прямой.
РАССТОЯНИЕ ОТ ТОЧКИ ДО ФИГУРЫ

РАССТОЯНИЕ ОТ ТОЧКИ ДО ФИГУРЫ
Нахождение расстояния от точки до прямой.

Расстояние от точки А до прямой m − длина АК.
РАССТОЯНИЕ ОТ ТОЧКИ ДО ФИГУРЫ
АK = 11 см

РАССТОЯНИЕ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ

РАССТОЯНИЕ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ
Нахождение расстояния между прямыми а и b (а ∥ b).

РАССТОЯНИЕ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ
Нахождение расстояния между прямыми а и b (а ∥ b).

РАССТОЯНИЕ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ
Нахождение расстояния между прямыми а и b (а ∥ b).

РАССТОЯНИЕ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ
Нахождение расстояния между прямыми а и b (а ∥ b).

РАССТОЯНИЕ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ
Нахождение расстояния между прямыми а и b (а ∥ b).

РАССТОЯНИЕ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ
Нахождение расстояния между прямыми а и b (а ∥ b).

РАССТОЯНИЕ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ
Нахождение расстояния между прямыми а и b (а ∥ b).

РАССТОЯНИЕ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ
Нахождение расстояния между прямыми а и b (а ∥ b).

РАССТОЯНИЕ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ
Нахождение расстояния между прямыми а и b (а ∥ b).

РАССТОЯНИЕ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ
Нахождение расстояния между прямыми а и b (а ∥ b).

РАССТОЯНИЕ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ
Нахождение расстояния между прямыми а и b (а ∥ b).

РАССТОЯНИЕ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ
Нахождение расстояния между прямыми а и b (а ∥ b).

РАССТОЯНИЕ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ
Расстояние между прямыми а и b − длина MN.
MN= 10 см

Рельсы на прямолинейном участке должны быть параллельными: они не могут сближаться или удаляться.
РАССТОЯНИЕ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ

Поэтому их крепят к шпалам на одном и том же расстоянии
друг от друга. Это расстояние называют шириной колеи.
РАССТОЯНИЕ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ

РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ

Как найти расстояние от светильника до пола?
РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ

Расстояние от точки до плоскости измеряют по перпендикуляру.
РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ

ABCDKLMN – куб. Ребро АВ перпендикулярно грани AKND.
РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ

РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ
ABCDKLMN – куб. Ребро АВ перпендикулярно грани AKND. Расстояние от точки В до плоскости AKND равно длине АВ.

РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ
ABCDKLMN – куб. Ребро ВС перпендикулярно грани СМND.

РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ
ABCDKLMN – куб. Ребро ВС перпендикулярно грани СМND. Расстояние от точки В до плоскости СМND равно длине ВС.
На этой странице вы узнаете
- Как найти расстояние между мухой и столбом?
- Как любопытный кот, скидывая вкусняшки со стола, нашел расстояния от точки до плоскости и от прямой до плоскости?
- Внимание! Сложные расчеты! Как любопытному коту найти расстояние между плоскостью стола и полом?
Отправляясь в любое путешествие, мы проверяем, как далеко нам придется ехать. На пробежке мы смотрим, какое расстояние преодолели. А пробег на машине? Если мы с такой легкостью считаем расстояния в нашей жизни, неужели в математике должно быть что-то сложнее?
Расстояния между фигурами
Когда нам нужно дойти от дома до магазина, мы можем точно сказать, какое расстояние нам нужно пройти. Например, магазин находится в 200 метрах от дома, следовательно, мы и должны пройти 200 метров, чтобы купить что-то вкусненькое.
Таким образом, мы получаем расстояние между двумя точками.
Расстояние между точками — это длина отрезка, заключенного между ними.

Пока мы шли в магазин, мы заметили на столбе интересное объявление о продаже цветов. Как найти расстояние от нас до этого объявления? Разумеется, пройти определенное расстояние до столба. Допустим, это будет 5 метров.
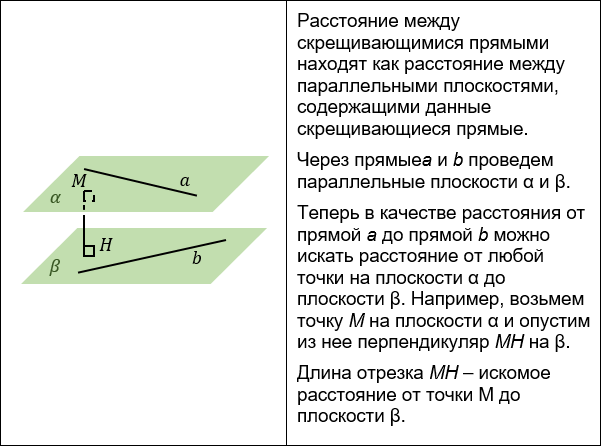
Заметим, что мы прошли по асфальту, то есть по горизонтальной поверхности. А мы и столб стоим вертикально, то есть перпендикулярны поверхности асфальта. Обратим внимание, что при этом мы со столбом будем параллельными прямыми.
Следовательно, мы пришли к выводу, что:
Расстояние между параллельными прямыми — это длина перпендикуляра, проведенного между ними.
Иными словами, это отрезок, который мы прошли по асфальту.
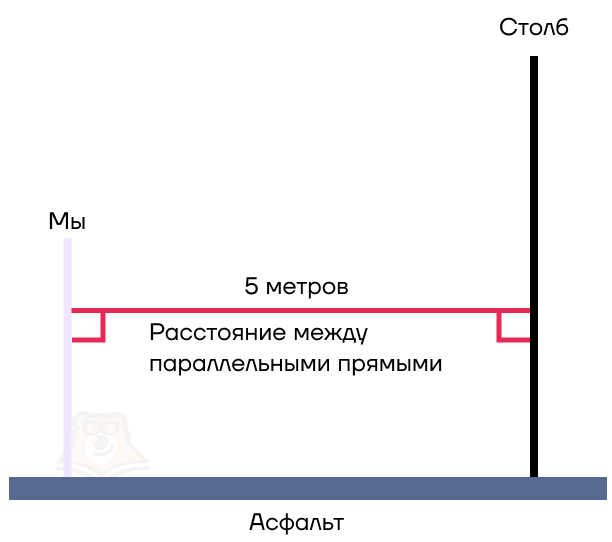
Но как только мы собрались дойти до столба и сорвать объявление, прямо мимо наших глаз пролетела муха. Она летела строго на одной высоте, долетела до столба и села на объявление.
Как найти в этом случае расстояние между мухой и столбом? На самом деле, муха пролетела ровно такое же расстояние, которое нам необходимо было пройти до столба.
Поскольку муха совсем маленькая, возьмем ее за точку. И таким образом, мы получаем расстояние между точкой и прямой.
Расстояние между точкой и прямой — это длина перпендикуляра, опущенного из этой точки на прямую.
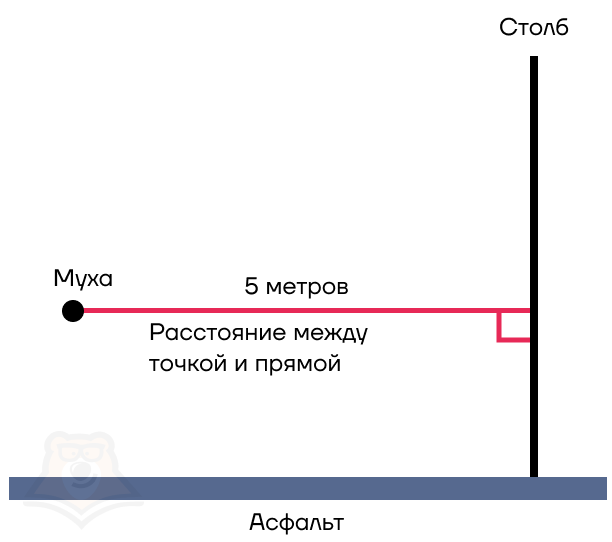
Для этого достаточно найти расстояние между точкой и прямой — длину перпендикуляра, опущенного из этой точки на прямую.
Пока мы злились на муху за то, что она опередила нас и добралась до объявления первой, мимо нас прошли грузчики, которые несли вешалку под углом к асфальту и столбу. Чему тогда будет равно расстояние между вешалкой и столбом?
Мы не можем точно сказать, что 5 метров, поскольку вешалка не параллельна столбу. Чтобы его найти, достаточно провести перпендикуляр и к столбу, и к вешалке.
Так мы нашли расстояние между скрещивающимися прямыми. Подробнее о скрещивающихся прямых можно прочесть в статье «Аксиомы стереометрии. Прямые и плоскости в пространстве».
Расстояние между скрещивающимися прямыми — длина их общего перпендикуляра.
Удивившись тому, как много всего может произойти только со столбом, мы все-таки дошли до магазина, купили тортик и рулетик и вернулись домой. Поставили покупки на стол и пошли готовить чай.
В этот момент на стол запрыгнул наш кот и решил проверить, какое расстояние от тортика до пола. И для этого он скинул наш тортик со стола.
Существует ли возможность измерить расстояние от тортика до пола, при этом не жертвовать этим самым тортиком? Представим, что пол — это плоскость, а тортик — точка. Тогда нам всего лишь нужно найти расстояние от точки до плоскости.
Расстояние от точки до плоскости — это длина перпендикуляра, опущенного из этой точки на плоскость.
Так и есть: когда кот скинул тортик, он пролетел строго вертикально до пола.
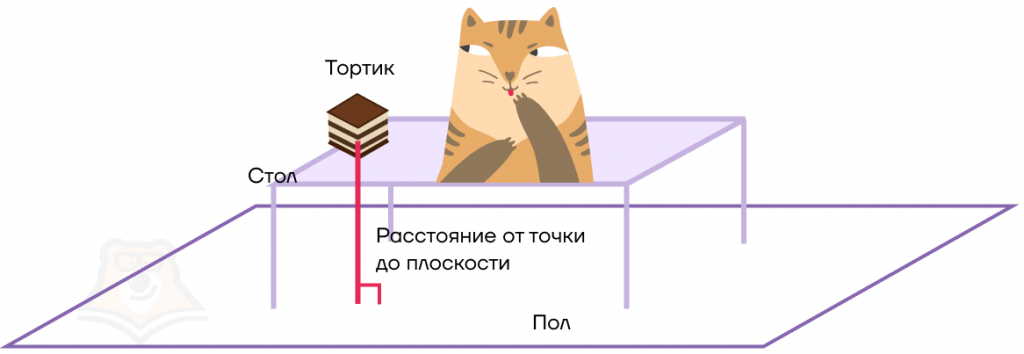
Наш кот посмотрел на упавший торт и тут резко заметил, что мы принесли еще и очень длинный рулетик! Теперь ему стало интересно, какое расстояние от рулетика до пола, поэтому он решил скинуть и его.
Расстояние от рулетика до пола можно было найти и другим способом, а именно найти расстояние от прямой до плоскости. Поскольку рулетик лежит на столе, то он параллелен полу.
Расстояние между прямой, параллельной плоскости, и плоскостью — это длина перпендикуляра, опущенного из любой точки этой прямой на плоскость.
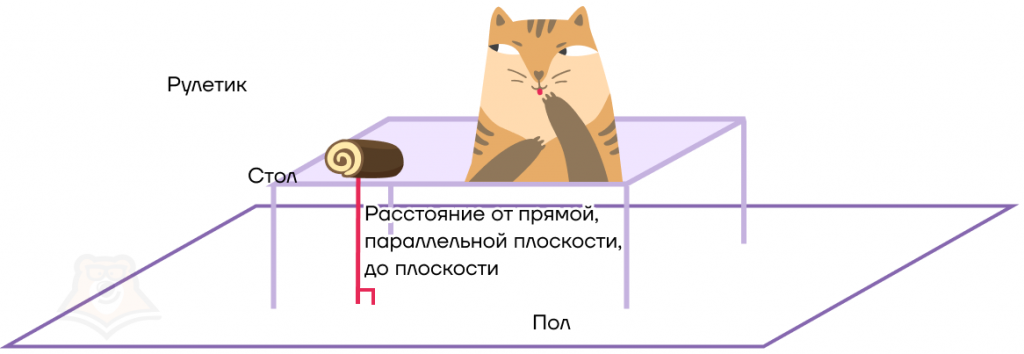
Заметим, что если прямая не параллельна плоскости, то рано или поздно она ее пересечет, а значит, точного расстояния между ними не будет.
Оказывается, наши вкусняшки пролетели строго вертикально вниз, то есть преодолели длину перпендикуляра, проведенного от них до пола!
Таким образом, расстояние от точки до плоскости — это длина перпендикуляра, опущенного из этой точки на плоскость.
Расстояние между прямой, параллельной плоскости, и плоскостью — длина перпендикуляра, опущенного из любой точки этой прямой на плоскость.
Увидев, что он скинул все продукты питания, кот решил сбежать с места преступления. Но перед этим он задался вопросом, какое расстояние от плоскости столешницы до плоскости пола, чтобы рассчитать свой прыжок.
Но и в этом ему на помощь могла прийти стереометрия. Как жаль, что кот ее не знает, поэтому все проверяет на практике.
Теперь нам нужно найти расстояние между параллельными плоскостями.
Расстояние между параллельными плоскостями — это длина перпендикуляра, опущенного из любой точки одной плоскости на вторую плоскость.
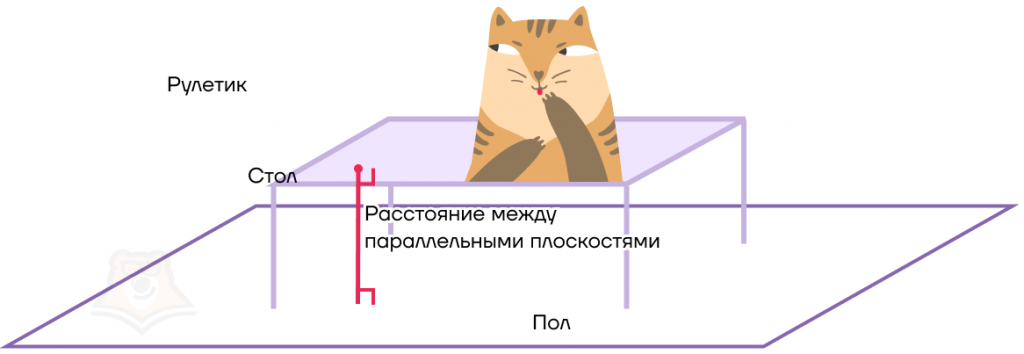
Для этого ему также нужно найти, сколько он пролетит строго вниз. Или, иначе говоря, расстояние между параллельными плоскостями — это длина перпендикуляра, опущенного из любой точки этой плоскости на вторую плоскость.
Вот так, благодаря одной прогулке до магазина и любопытству кота, мы рассмотрели, как находятся расстояния между двумя фигурами. Ничего сложного, верно?
При решении задач, конечно, в условии не встретишь любопытного кота или муху на объявлении, но кто мешает включать нам фантазию и представить условие задачи как жизненные ситуации.
Фактчек
- Расстояние между точками — это длина отрезка между ними. Расстояние между точкой и прямой — это длина перпендикуляра, опущенного из этой точки на прямую.
- Расстояние между параллельными прямыми — это длина перпендикуляра, проведенного между ними. Расстояние между скрещивающимися прямыми — длина их общего перпендикуляра.
- Расстояние от точки до плоскости — это длина перпендикуляра, опущенного из этой точки на плоскость.
- Расстояние между прямой, параллельной плоскости, и плоскостью — это длина перпендикуляра, опущенного из любой точки этой прямой на плоскость.
- Расстояние между параллельными плоскостями — это длина перпендикуляра, опущенного из любой точки одной плоскости на вторую плоскость.
Проверь себя
Задание 1.
Как найти расстояние между точкой и прямой?
- Найти длину любой линии от этой точки до прямой.
- Найти длину перпендикуляра, опущенного из этой точки на прямую.
- Невозможно найти расстояние между точкой и прямой.
- Ни один из вышеперечисленных вариантов.
Задание 2.
Как найти расстояние между скрещивающимися прямыми?
- Найти длину произвольной прямой между ними.
- Найти длину прямой, перпендикулярной одной из прямых и не перпендикулярной второй прямой.
- Найти длину их общего перпендикуляра.
- Невозможно найти расстояние между скрещивающимися прямыми.
Задание 3.
Как найти расстояние от точки до плоскости?
- Найти длину перпендикуляра, опущенного из этой точки на плоскость.
- Найти длину произвольной линии, проведенной из точки к плоскости.
- Найти расстояние от точки до любой прямой, лежащей в плоскости.
- Невозможно найти расстояние между точкой и плоскостью.
Задание 4.
Как найти расстояние от прямой до плоскости?
- Найти длину произвольной линии, проведенной из любой точки этой прямой до плоскости.
- Найти длину отрезка, соединяющего любую точку на прямой и любую прямую в плоскости.
- Найти длину перпендикуляра, опущенного из любой точки этой прямой на плоскость.
- Невозможно найти расстояние между прямой и плоскостью.
Задание 5.
Как найти расстояние между параллельными плоскостями?
- Невозможно найти расстояние между параллельными плоскостями.
- Найти длину перпендикуляра, опущенного из любой точки одной плоскости на вторую плоскость.
- Найти длину отрезка, соединяющего точку одной плоскости с произвольной точкой на второй плоскости.
- Найти длину отрезка, соединяющего две произвольные прямые в плоскостях.
Ответы: 1. — 2 2. — 3 3. — 1 4. — 3 5. — 2
Рассмотрим
только определение расстояний, поскольку
НВ плоской фигуры была рассмотрена в
п. 4.
8.1. Расстояние от точки до фигуры (точки, прямой, плоскости)
Приведем сведения
из планиметрии, необходимые для решения
обозначенных задач.
1. Длина отрезка
есть расстояние между его концами.
2. Из точки, не
лежащей на прямой, можно провести
перпендикуляр к этой прямой, и притом
только один.
 Задача. Определить
Задача. Определить
длину отрезка АВ (рис. 8.1).
В п. 4 было
приведено решение этой задачи методом
замены плоскостей проекций. Рассмотрим
другое решение – решение методом
прямоугольного треугольника. Его
обоснование выполним, опираясь на
указанный метод замены. Выполняя решение
данной задачи методом замены, получим
А4В4
– искомую
длину. Видим, что в соответствии с методом
замены Е4В4
= b.
Поэтому, отложив на линии В1В4
^
х1 от
точки В1
отрезок
B1D1
= E4В4
= b,
получим прямоугольный треугольник
А1В1D1
, в котором
А1D1
= А4В4
, т.е. длина
гипотенузы А1D1
есть искомая
длина. Следовательно, длину отрезка АВ
можно определить на плоскости проекций
П1 используя
расстояние b,
снятое на плоскости проекций П2
. При этом
замена плоскостей проекций с осью х1
не нужна.
Аналогично можно определить искомую
длину на плоскости П2
. Для этого
выстраиваем прямоугольный треугольник
B2A2C2
, у которого
С2А2
= а, где а
определено на П1
. В итоге
получаем В2С2
= В1С1
– искомая
длина отрезка АВ. Понятно, что необходимо
строить лишь один из двух приведенных
прямоугольных треугольников.
Задача.
Даны прямая АВ и точка Е вне прямой (рис.
8.2). Требуется определить расстояние
(Е, АВ).
 Проекционный
Проекционный
алгоритм решения может быть следующим:
1) методом замены
плоскостей проекций определяется длина
отрезка АВ. На П4
она равна
А4В4
;
2) строится
дополнительная на П4
проекция
Е4 точки
Е;
3) вводится новая
система плоскостей проекций П4,
П5 такая,
что ее ось проекций х2
перпендикулярна
А4В4;
4) на П5
строятся
дополнительные
проекции отрезка
АВ и точки Е. Проекциями будут соответственно
точки А5 =
В5 и
Е5 .
Расстояние
(F5,
Е5)
является искомым расстоянием между
данными прямой и точкой. Возвращаем
затем последовательно проекции отрезка
EF
на П4,
П1,
П2.
Для этого проводим вначале E4F4
// x2
, а затем
строим: (F5,
F4
)
F1
; (F4
, F1
)
F2.
 В итоге получаем
В итоге получаем
E1F1
, E2F2
– основные
проекции отрезка EF,
длина которого есть искомое расстояние.
Необходимо отметить, что если не учитывать
полученные построения на П5
, то оставшиеся
построения на П2,
П1 и
П4 соответствуют
решению задачи о проведении прямой EF
через данную точку Е, пересекающей под
90
данную прямую АВ.
Задача.
Даны плоскость Σ (ΔАВС)
и точка Е. Определить расстояние от
точки Е до плоскости Σ (рис. 8.3).
Решение задачи
может быть выполнено методом замены
плоскостей проекций. Проекционный
алгоритм решения в этом случае следующий:
1) в плоскости
Σ строится линия уровня,
например h(h1,
h2)
, так, что h2
// x;
2) вводится новая
система плоскостей проекций П1,
П4 с
осью х1
так, что х1
^
h1;
3) на П4
строятся
дополнительные проекции заданных фигур
– В4С4
для ΔАВС
и Е4 для
точки Е;
4) длина
перпендикуляра E4F4
есть искомое
расстояние (Е,
Σ).
Для полноты
решения строим проекции отрезка EF
на основных плоскостях проекций. Для
этого строим вначале E1F1
// х1
, а затем
(F4
, F1)
F2
; E2F2
, E1F1
–
основные проекции отрезка EF
длины .
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #