Как найти расстояние от точки до графика - Сайт, где вы сможете решить свои вопросы

Лучший ответ

0 Голосов

Posted Октябрь 19, 2013 by Вячеслав Моргун

Нам нужно найти координаты точки принадлежащей графику функции расстояние от которой до т. M будет наименьшим. Расстояние между двумя точками на плоскости рассчитывается по следующей формуле: $$S= sqrt{(x-x_0)^2+(y-y_0)^2}$$где ((x_0;y_0)) – это координаты точки M(-2;0), а ((x;y)) -координаты точки, которая принадлежит графику функции, которую нужно найти. Подставим известные координаты в уравнение $$S = sqrt{(x+2)^2+(y-0)^2}$$
В задании стоит слово наименьшее, это уже указывает на необходимость поиска экстремумов, т.е. нужно найти точку минимума функции (S(x;y)), т.е. нудно найти первую производную от расстояния S между точками и приравнять ее к нулю (S’=0). В уравнении x и y принадлежат графику функции, поэтому выразим y через x $$S = sqrt{(x+2)^2+(-sqrt{2-x})^2} = sqrt{(x+2)^2+2-x}$$теперь найдем производную и приравняем ее к нулю. $$S’ = (sqrt{(x+2)^2+2-x})’ = frac{2(x+2)-1}{2*sqrt{(x+2)^2+2-x}} =0$$Дробь будет равна нулю, если числитель равен нулю $$2(x+2)-1=0 =>2x+4-1=0=>x=-frac{3}{2}$$ Получили координату x, подставляем ее в уравнение графика функции и получаем (y = -sqrt{2-x} = -sqrt{2 +frac{3}{2}} = -sqrt{frac{7}{2}}). Получили координаты точки (N(-frac{3}{2};-sqrt{frac{7}{2}})) – это и будет искомая точка. Для полноты расчетов необходимо проверить, является ли эта точка точкой минимума, подставим значение x левее и правее точки минимума в производную и проверим знак производной:
S'(-3) < 0
S'(0) > 0, т.е. найденная нами точка (N(-frac{3}{2};-sqrt{frac{7}{2}})) – точка минимума.

Получим искомое расстояние, подставив координаты этой точки в формулу расстояния $$S_{min} = sqrt{(x+2)^2+y^2} = sqrt{(-frac{3}{2}+2)^2+frac{7}{2}}=sqrt{frac{1}{4}+frac{7}{2}} = frac{sqrt{15}}{2}$$ Наименьшее расстояние между точкой и кривой (S=frac{sqrt{15}}{2})

На рисунке график функции:
(y = -sqrt{2-x}) – черным
(S = sqrt{(x+2)^2+2-x}) – красным
(S_1 = -sqrt{(x+2)^2+2-x}) – зеленым – симметричное отображение графика расстояния относительно от Ox для наглядности (S=|S_1|).

Источник

Помогите решить задачу: надо найти расстояние от точки до графика

Мастер

(1711),
закрыт

15 лет назад

Дополнен 15 лет назад

V – корень

Юрий Семыкин

Искусственный Интеллект

(157599)

15 лет назад

Расстояние между двумя точками, квадрат расстояния: (х1-х2)^2+(у1-у2)^2==
(х-0)^2+(f(x)-1)^2 = x^2+(3x^3)/32 находим производную 2х+(9/32)х^2 приравниваем 0, получим 0 и – 64/9 Исходное уравнение имеет смысл при х>=0. Проверим, что х=0 минимум, получим 1- мин расстояние.

Alexander AlenitsynВысший разум (754583)

15 лет назад

) Условие задачи записано автором вопроса непонятно. Как Вы расшифровали странную черту над формулой? Из чего извлекается корень ?

3/2 – это показатель степени? Или показатель =3 ?

Школьники перестали ставить скобки! И теперь их понять невозможно.

2) Вопрос к автору ответа: Откуда в скобке (f(x)-1) взялась лишняя единица, которая так удачно скомпенсировала вычитаемую единицу?

Источник

геометрия – Расстояние от точки до функции

Необходимо написать функцию, которая вычисляет минимальное расстояние от точки p до функции $$f(x) = Asin(Bx + C) + D$$
Написал функцию определяющую расстояние
$$r^2 = (x−p.x)^2 + (f(x) – p.y)^2$$
Производная исходной функции $$f'(x) = ABcos(Bx + C)$$
Пытаюсь найти минимальное значение функции определяющей расстояние
$$(r^2)’ =2x – 2p.x + 2f'(x)f(x) – (2p.y)f'(x) = 0$$
Подставляю значения функций f(x) и f'(x)
$$(r^2)’ = 2x – 2p.x + 2ABcos(Bx+C)(Asin(Bx+C)+D) – (2p.y)ABcos(Bx+C) = 0 $$
$$(r^2)’ = x – p.x + ABcos(Bx+C)(Asin(Bx+C) +D – p.y) = 0 $$
$$x – p.x + ABcos(Bx+C)(Asin(Bx+C) +D – p.y) = 0 $$
Каким образом из данного равенства находится x ? Или возможно есть более действенный способ найти минимальное расстояние либо минимальное значение функции?

Здравствуйте

Математика – это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.

Присоединяйтесь!

отмечен:

геометрия
×3,291

задан
21 Апр ’18 19:53

показан
803 раза

обновлен
21 Апр ’18 22:57

Связанные исследования

Связанные вопросы

Отслеживать вопрос

по почте:

Зарегистрировавшись, вы сможете подписаться на любые обновления

по RSS:

Ответы

Ответы и Комментарии

Источник

воскресенье, 05 июня 2011

10:24

Расстояние от точки до графика

все записи пользователя в сообществе

Krysty

Всем привет! Помогите, пожалуйста, с заданием, хотя бы подскажите, с чего начать Тут явно что-то надо делать с касательной и, возможно, искать производную, но я не знаю уравнение касательной и составить его нельзя.
Итак, вот: “Найдите квадрат наименьшего расстояния от точки A(-2;1) до графика функции Y = x^2 + 1/2”. Спасибо
Решено

@темы:

ЕГЭ

URL

← Предыдущая запись
Следующая запись →

Источник

Комментарии преподавателя

Задачи на расстояние от точки до кривой

1. Опорные факты

Что такое расстояние от точки докривой? Точку можно соединить со многими точками кривой. Каждый раз будут получаться разные расстояния. Среди них нужно найти наименьшее. Это расстояние и будет называться расстоянием от точки до кривой. На кривой надо найти такую точку , чтобы расстояние было наименьшим (см. рис. 1).

Рис. 1. Расстояние от точки до кривой.

Видим, что задача на расстояние – это задача на экстремум, на минимум, то есть без производной не обойтись.

Вспомним, что расстояние от точки до прямой – это длина перпендикуляра (см. рис.2).

Рис. 2. Расстояние от точки до прямой.

Расстояние между прямыми – это тоже длина перпендикуляра (см. рис.3).

Рис. 3. Расстояние между прямыми.

Расстояние от точки до окружности легко найти. Нужно соединить центр с точкой , в результате получится точка . – искомое расстояние (см. рис.4).

Рис. 4. Расстояние от точки до окружности.

Расстояние между двумя окружностями, которые не пересекаются. Нужно соединить центры, получим две точки и . – искомое расстояние (см. рис.5).

Рис. 5. Расстояние между двумя окружностями.

Сформулируем задачу в общем виде и напомним, каким образом ее решать. Мы повторили, что такое расстояние. Вспомним формулу расстояния между двумя заданными точками. Предположим, что на координатной плоскости даны две точки и (см. рис.6).

Рис. 6. Расстояние между двумя заданными точками.

Расстояние между точками вычисляется по формуле

Таким образом, находится расстояние между точками, если известны координаты этих точек.

2. Задача 1

На параболе найти точки ближайшие к началу координат, то есть к точке .

Рис. 7. График функции.

Решение.

Из простейшего анализа задачи можно увидеть, что задача имеет два решения, в силу симметрии графика функции относительно оси Y (см. рис.7).

Координаты искомой точки: . По соответствующей формуле можем найти квадрат расстояния:

. Это расстояние должно быть наименьшим. Упростим эту формулу и получим:

или

Можно сразу использовать производную для решения задачи, но пока попытаемся воспользуемся свойствами биквадратной функции. С помощью замены переменной , получим:

. Задача свелась к нахождению минимума следующей квадратичной функции . Найдем абсциссу вершины (см. рис.8).

Рис. 8. Абсцисса вершины параболы.

Задача практически решена. Наименьшее значение этой функции будет тогда, когда . Вычислим . Значит, функция ведет себя следующим образом (см. рис.9):

Рис. 9. Схематический график функции .

Без производной, с помощью свойств квадратичной функции, решили задачу. Если , то , отсюда , . Если значения координат известны, вычислим значения . ; Получили ответ ; .

Итак, была задача: найти точки на кривой, которые бы отстояли от начала координат на наименьшее расстояние. Такие точки найдены. Первая точка – , вторая точка – .

Напомним ход решения задачи. Точка зависит только от , ее координаты – . При выражении квадрата расстояния, получили функцию от . Можно с помощью производной найти минимум. Можно сделать проще. Если сделать замену , получим квадратичную функцию и можно найти наименьшее значение данной квадратичной функции.

Ответ: .

3. Задача 2

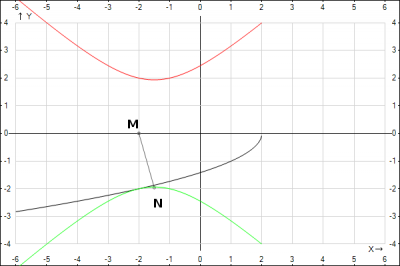
На графике функции найти точку , ближайшую к данной точке . Решение.

Сделаем рисунок (см. рис.10).

Рис. 10. График функции .

Заданы координаты двух точек: и .

Найдем расстояние АМ:

или .

– квадратичная функция от . Вспомним, что нужно найти минимальное значение, то есть . Графиком этой функции является парабола, ветвями направленная вверх, значит, минимум находится в вершине. Выделим полный квадрат и получим:

. Выяснилось, что . Равенство достигается, когда принимает самое минимальное значение. Это будет в случае, когда . Таким образом, получили ответ , а . Значит, координаты точки .

Ответ: .

4. Итог

Итак, мы рассмотрели задачи на расстояние от точки до кривой. Можно находить само это расстояние, можно искать точки, которые обеспечивают минимум этого расстояния. Повторили, что такое расстояние между фигурами. Расстояние от точки до кривой – это наименьшее из расстояний, которое получается, когда точка на кривой пробегает все возможные значения. Например, точка может пробегать все значения на кривой , но наименьшее расстояние будет тогда, когда точка имеет координаты . Для этого нужно, во-первых, вспомнить, что такое расстояние, и во-вторых, каким образом ищется расстояние между точками, если известны координаты. И, наконец, надо записать квадрат расстояния и проанализировать полученную функцию. Если не удается это сделать элементарными средствами, с помощью свойств квадратичной функции, то надо использовать производную и искать наименьшее значение функции .

Типовые задачи на производную с иррациональными функциями

5. Техника дифференцирования

Важнейшие задачи на производную с иррациональными функциями – это задачи на экстремум. Прежде всего, нужно вспомнить технику дифференцирования.

Повторим ее на следующем примере.

Дана функция . Найти .

Напомним, что .

. – постоянная величина, так как в данном выражении нет переменной, а . Отсюда, .

Следующее действие – найти производную в конкретной точке.

. Таким образом, нашли производную в данной точке. Значит, первая типовая задача, есть там иррациональность или нет, решается стандартным образом. Если нужно найти производную в конкретной точке, ищем производную в любой точке , а потом подставляем нужное значение.

6. Исследование функции и построение графика (задача 1)

Построить график функции .

Сначала надо попытаться все сделать без производной и понять эскиз графика функции.

1. Интервалы знакопостоянства функции.

: .

Найдем корни (нули) функции: или .

Во всех точках области определения функция положительна, значит, график будет находиться над осью (см. рис.1).

Рис. 1. Интервалы знакопостоянства функции .

2. Построить график в окрестности каждого корня.

Функция в точке равна нулю. Справа и слева от точки функция положительна, значит, в точке функция имеет экстремум, производная должна это подтвердить. В точке функция тоже рана нулю. Значит, функция ведет себя следующим образом (см. рис.2):

Рис. 2. Схематический график функции в окрестности каждого корня.

Точек разрыва нет, и когда , то . Значит, график функции выглядит следующим образом (см. рис.3):

Рис. 3. Схематический график функции при .

Построили эскиз графика функции.

3. Проведем исследование функции с помощью производной и выясним интервалы знакопостоянства производной.

Приравняем производную к нулю и найдем критические точки:

отсюда .

Оба значения принадлежат области определения.

Найдем интервалы знакопостоянства производной. Сделаем иллюстрацию (см. рис.4):

Рис. 4. Интервалы знакопостоянства производной.

Итак, – точка максимума, так как производная меняет знак с «+» на «-» (см. рис.4). Найдем значение функции в этой точке:

. Точка – точка минимума, так как производная меняет знак с «-» на «+». Вычислим .

Таким образом, можем построить график функции (см. рис. 5).

Рис. 5. График функции .

7. Решение задачи с параметром

Дано уравнение . Найти положительное значение параметра , при котором уравнение имеет ровно два различных решения.

Решение.

Воспользуемся графиком функции (см. рис.5). При уравнение имеет два различных корня, но по условию поэтому .

Ответ: При .

Итак, мы рассмотрели функцию , где есть иррациональность, исследование и построение графика. Методика построения графика функции следующая: построить эскиз графика функции без использования производной (интервалы знакопостоянства функции, поведение функции в окрестности точек разрыва области определения, в окрестности корней и бесконечно удаленных точек). Потом исследование с помощью производной уточняет график функции.

8. Исследование функции и построение графика (задача 2)

Построить график функции .

Решение.

Эта функция иррациональная. Методику применяем ту же самую. Сначала попытаемся построить эскиз графика функции без производной.

: .

Найдем нули функции.

или . Определим знак функции на каждом интервале (см. рис.6).

Рис. 6. Интервалы знакопостоянства функции.

Итак, знаем, что на промежутке график функции будет находиться над осью , а на промежутке – под осью .

Построим график функции в окрестности каждого корня (см. рис.7).

Рис. 7. Схематический график функции в окрестности каждого корня.

Если , то . График идет следующим образом (см. рис.8):

Рис. 8. Эскиз графика функции .

Мы предполагаем, что на промежутке должен быть экстремум (см.рис.8). На все вопросы даст ответ производная.

Проведем исследование функции с помощью производной.

Приравняем производную к нулю, получим:

, отсюда – единственная точка области определения функции, в которой производная равна нулю. Найдем интервалы знакопостоянства производной (см. рис.9):

Рис. 9. Интервалы знакопостоянства производной.

Осталось вычислить значение функции в точке .

. Итак, координаты точки экстремума таковы:

Рис. 10. График функции .

Если мы провели полное исследование функции и построили график, то на любые типовые вопросы, связанные с этой функцией, мы можем получить ответы.

Например, найти все значения параметра , при которых уравнение не имеет решений.

Ответ: если уравнение не имеет решений, значит параметр не входит в множество значений функции (см. рис. 10).

Рис. 10. Множество значений функции.

Ответ: уравнение не имеет решений при всех .

9. Итог

Итак, мы рассмотрели типовые задачи на производную для тех функций, в которых присутствует иррациональность. Вспомнили, как дифференцируются такие функции, каким образом исследуются функции, и как строятся графики функций.

ИСТОЧНИК

http://interneturok.ru/ru/school/algebra/10-klass/proizvodnaya/zadachi-na-rasstoyanie-ot-tochki-do-krivoy

http://interneturok.ru/ru/school/algebra/10-klass/proizvodnaya/tipovye-zadachi-na-proizvodnuyu-s-irratsionalnymi-funktsiyami

http://www.youtube.com/watch?v=iOz-YH_48GU

http://www.youtube.com/watch?v=t2tyJqTSn8U

http://znanija.com/task/2437276

https://downloader.disk.yandex.ru/disk/779ef72b0b73617de61c4dc2c21838459e86176ed8f801b37481d34346768467/56a16f54/KmTYbqVG3TgKGL9iUHPR0em0RlLtpxhP_BVgRtkosSgfwonkMOj8PI__aMfad3WZY71hHToni_M3mTC7aMwq3A%3D%3D?uid=0&filename=666.PDF&disposition=attachment&hash=RaLDsjqwggBTdSmademPwU40mOjt%2BFWdduHVDt9R80E%3D&limit=0&content_type=application%2Fpdf&fsize=8352787&hid=021760e85b03ef221c6c4091fc10c607&media_type=document&tknv=v2

Источник

Лучший ответ

Помогите решить задачу: надо найти расстояние от точки до графика

геометрия – Расстояние от точки до функции

Здравствуйте

Связанные исследования

Связанные вопросы

Отслеживать вопрос

Расстояние от точки до графика

Комментарии преподавателя

1. Опорные факты

2. Задача 1

3. Задача 2

4. Итог

5. Техника дифференцирования

6. Исследование функции и построение графика (задача 1)

7. Решение задачи с параметром

8. Исследование функции и построение графика (задача 2)

9. Итог

Вам также может понравиться

Как составить официа

Как найти вход в градирнях

Как найти течь в перекрытии

Добавить комментарий Отменить ответ