So, the task is to find a minimum distance from a given point $T$ to cone. The cone is represented with points $a,b,c$, where points $a$ and $b$ form a line that represent a symmetry axis, and points $a$ and $c$ form a line that represents slant height of the cone. All $a,b$ and $c$ are of type Point: $x,y,z in R^3$.
Point is a class with $x,y,z$ members, and Cone is a class with a,b,c members of type Point.
I found the equations of those two lines by formula and also their intersection point, which would be the vertex of the cone, but how do I find the equation of the cone? And then how will I find the distance? Could I find a line which contains point $T$ that is normal to the surface of cone, and then somehow distance?
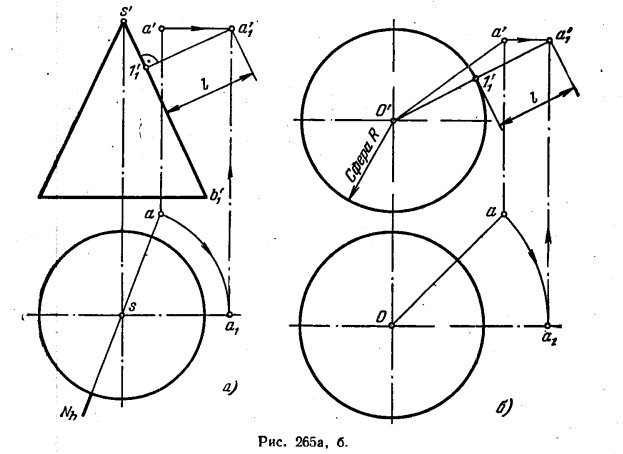
282*. Определить расстояние от точки А до ближайшей точки на поверхностях: а) конуса (рис. 265, а); б) сферы (рис. 265, б); в) тора (рис. 265, в).
Решение, а) Искомое расстояние (рис. 265, а) равно расстоянию от данной точки до ближайшей к ней образующей. Эта образующая лежит в пл. N, проходящей через точку А и ось конуса.
Поворачиваем эту плоскость вокруг оси конуса до положения, параллельного пл. V. Точка А займет положение A1(а1, a’1), и искомое расстояние выразится отрезком a’11′1, перпендикулярным к s’b’1.
б) На рис. 265, б показано, что искомое расстояние измеряется по прямой АО. Повернув прямую АО вокруг оси, проходящей через точку О перпендикулярно к пл. Н, так, чтобы АО стала параллельна пл. V, получим l = А1O — R =a’1O’— R.
в) Расстояние отточки А до поверхности тора (рис. 265, в) измеряется величиной отрезку нормали к поверхности тора в плоскости, проходящей через точку А и ось тора. Повернув эту плоскость вокруг оси тора до положения, параллельного пл. V, и проведя прямую a’1O’, получим точку 1′1 и отрезок а’11′ 1.Эго и есть нормаль к поверхности тора, проходящая через точку А1, а до поворота — через точку А.
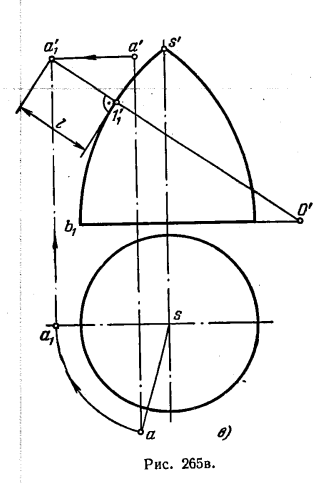
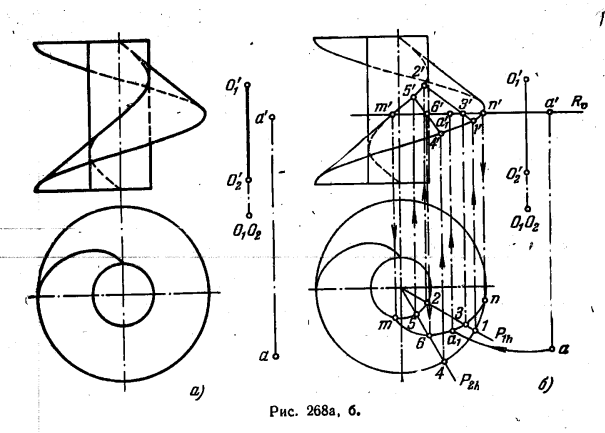
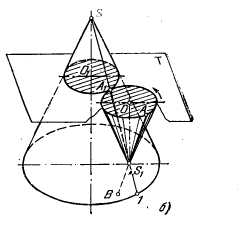
283*. Поворотом вокруг оси O1O2 точку А совместить с поверхностью конуса вращения (рис. 266, а).
Peшeниe. Поворот точки А вокруг оси O1O2 происходит в пл.T (рис. 266, б), перпендикулярной к О1О2. Центр дуги окружности, по которой перемещается точка А, находится в точке пересечения оси O1O2 с плоскостью вращения T. Ггоризонт. проекция этого центра совпадает с точками O1 и O2. Итак, проведя из точки O1(O2) дугу радиуса O1а, получим на этой дуге горизонт. проекцию точки АВ любом ее положении в пл. Т при повороте вокруг оси O1O2. Но чтобы точка А оказалась при этом на поверхности данного конуса вращения, надо, очевидно, взять параллель конической поверхности на уровне пл. T, т. е. окружность радиуса О’1′. На этой окружности и находим точку А, когда она при повороте вокруг оси O1O2 оказывается на поверхности заданного конуса. По горизонт. проекциям а1 и a2 находим проекции а’1 и а’2. В положении А1 точка А окажется невидимой относительно пл. V, а в положении А2 — видимой. Точка А в положениях А1 и А2 относительно пл. Н будет видимой.
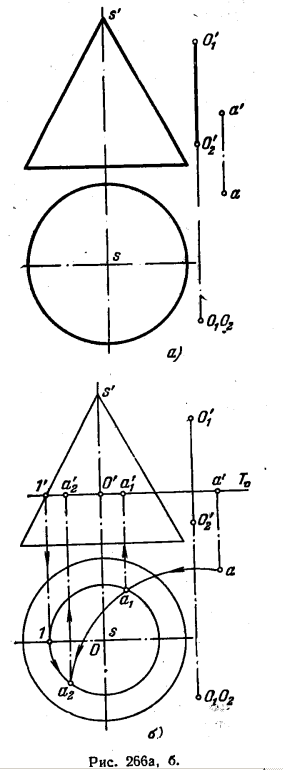
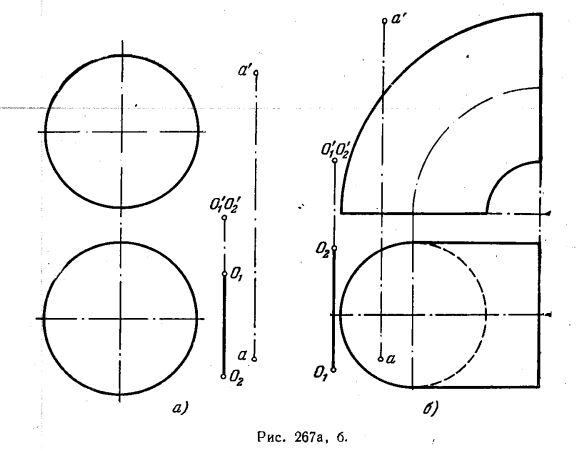
284. Поворотом вокруг оси O1O2 точку А совместить: а) с шаровой поверхностью (рис. 267, а); б) с поверхностью тора (рис. 267, б).
285*. Поворотом вокруг оси O1O2 точку А совместить с винтовой поверхностью (рис. 268, а).
Решение. Заданная косая винтовая поверхность имеет ось, параллельную оси O1O2. В указанном на чертеже положении поворот точки А происходит в пл. R (рис. 268, б), параллельной пл. Н и пересекающей данную поверхность по дуге спирали Архимеда. Строим горизонт. проекцию этой дуги, проводя для нахождения точек 3 и 6 плоскости Р1 и Р2 через ось поверхности. Они пересекают поверхность по ее образующим 1—2 и 4—5. Находим точки 3′ и 6′ в пересечении следа Rϑ с 1’2′.
и 4’5′, по ним строим проекции 3 и 6. Проводим через точки m, 6, 3 и n кривую и находим точку пересечения (а1) этой кривой с горизонт. проекцией окружности, описываемой точкой А. По а1 находим a’1: a1 и а’1 служат проекциями точки А в искомом положении.
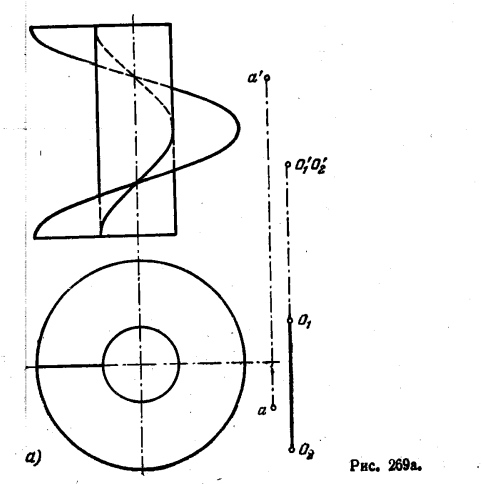
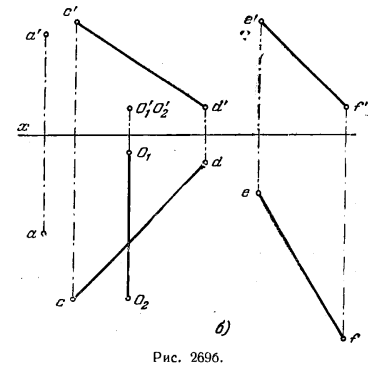
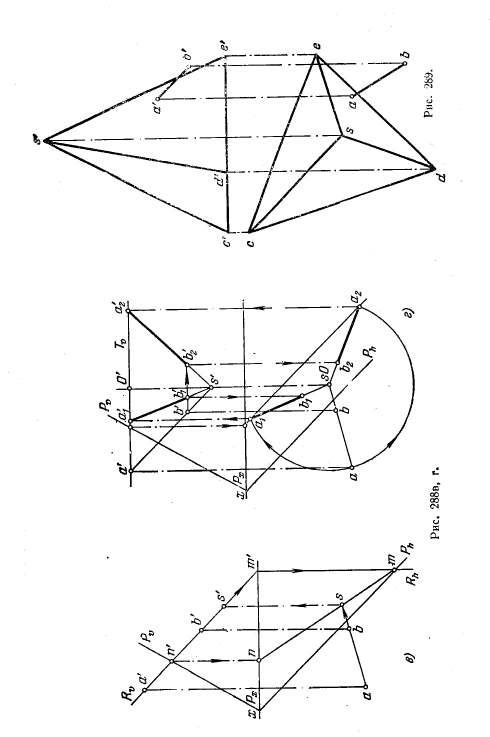
286. Поворотом вокруг оси О1O2 точку А совместить: а) с винтовой поверхностью (рис. 269, а); б) с косой плоскостью (рис. 269,6),
заданной направляющими прямыми CD и EF и плоскостью параллелизма H.
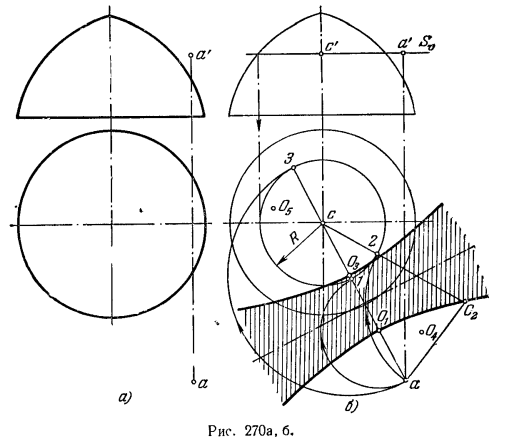
287*. Указать положения осей, перпендикулярных к пл. Н, поворотом вокруг которых можно ввести точку А на заданную поверхность вращения (рис. 270, а).
Решение. В отличие от задач 283 и 285 в данной задаче ось для поворота точки не задается; оговаривается лишь то, что эта ось должна быть перпендикулярна к пл. Н. Однако нельзя взять любую прямую, перпендикулярную к пл. Н, и принять ее за ось, пригодную для решения этой задачи.
На рис. 270, б показано, что имеется такая область, в которой было бы бесцельным брать точки в качестве горизонт. проекций осей вращения. Например, приняв точку O4 за горизонт проекцию оси, мы получим радиус вращения точки А равным O3а, но O4а меньше расстояния точки а до ближайшей точки на окружности радиуса R, и, следовательно, дуга радиуса O4а даже не коснется этой окружности. Или точка O5: совершенно очевидно, что дуга радиуса О6а не может иметь общих точек с окружностью радиуса R.
Но если взять точку О, так, чтобы О1а = О11, или точку О3 а так, чтобы О3а = О33, то в положениях 1 и 3 точка а окажется на окружности радиуса R. Взяв оси, прохот дящие через точки О1 и О3 перпендикулярно к пл. Н, мы можем решить задачу о введении точки А на заданную поверхность вращения. Легко видеть, что решение сводится к построению гиперболы, у которой фокусами служат точки а и с, а вершинами — точки О1 и О3. Эта гипербола определяет область (на рис. 270, б она заштрихована), в которой любая точка может быть принята за горизонт. проекцию оси, при повороте вокруг которой точка А окажется в двух положениях на данной
поверхности вращения. Если же точку взять на одной из ветвей гиперболы, то такая точка определяет ось, при повороте вокруг которой точка А окажется на поверхности вращения лишь в единственном положении. Например, точка О2: дуга радиуса О2а лишь коснется в точке 2 окружности радиуса R.
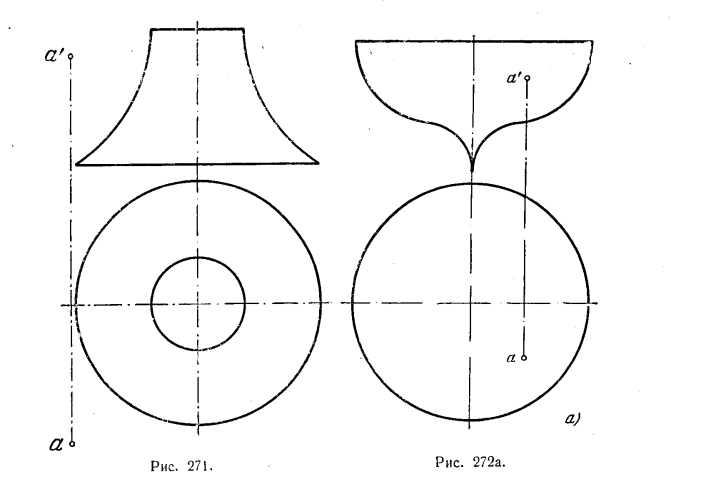
288. Указать положение осей, перпендикулярных к пл. H, поворотом вокруг которых можно точку А совместить с заданной поверхностью вращения (рис. 271).
289*. Указать положение осей, перпендикулярных к пл. H, поворотом вокруг которых можно точку А совместить с заданной по-верхностью вращения (рис. 272, а).
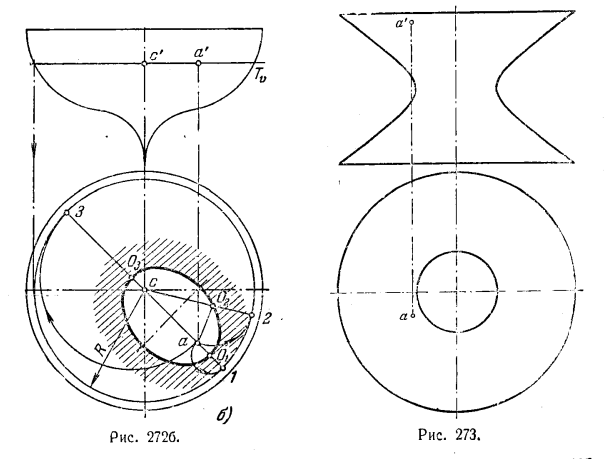
Решение. Отличие этой задачи от задачи 287* в том, что точка задана внутри поверхности вращения. Здесь также вопрос выбора положения осей решается при рассмотрении взаимного положения гочки А и окружности радиуса R (параллели) на поверхности вращения (рис. 272, б) Очевидно, что горизонт. проекция оси вращения (какая-либо точка О) должна быть расположена так, чтобы радиус Оа был не меньше расстояния точки О до ближайшей точки на окружности радиуса R. Предельные положения точки О (например, О1, О2 и др.) расположатся как точки эллипса с фокусами в точках а и с, с большой осью О1О3 на прямой 1—3. Точка O1 делит пополам отрезок а—1, а точка O3 — отрезок а—3. Если взять точки внутри этого эллипса и принять их за горизонт. проекции осей вращения, то вращением вокруг таких осей нельзя данную точку совместить с поверхностью вращения. горизонт. проекции осей надо брать или на эллипсе, или вне его.
290. Указать положения осей, перпендикулярных к пл. H, поворотом вокруг которых можно точку А совместить с заданной поверхностью вращения (рис. 273).
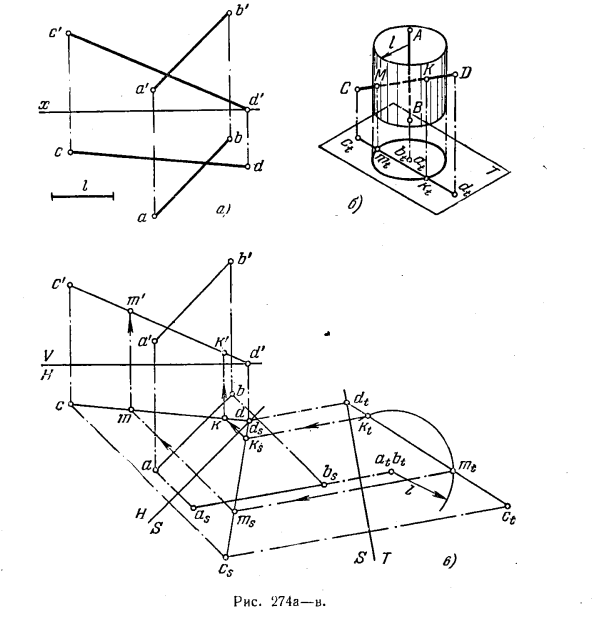
291*. На прямой CD найти точки, отстоящие от прямой АВ на расстояние l (рис. 274, а).
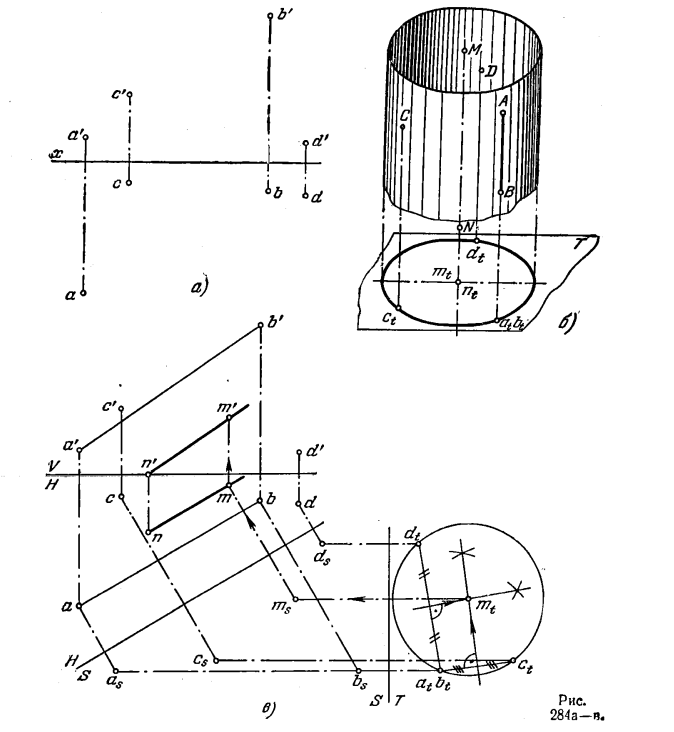
Решение. Геометрическим местом точек пространства, отстоящих от прямой АВ на расстояние l, является цилиндрическая поверхность с осью АВ и радиусом l
(рис. 274, б). Искомые точки М и К являются точками пересечения прямой CD с этой поверхностью.
Очевидно, для упрощения построения надо сделать так, чтобы ось цилиндрической поверхности оказалась перпендикулярной к какой-либо плоскости, принятой за плоскость проекций. Сначала (рис. 274, в) вводим пл. S⊥H и параллельно АВ, затем пл. T⊥S и ⊥AB. В системе Т, S прямая АВ перпендикулярна к пл. Т. Проекция цилиндрической поверхности на этой плоскости — окружность радиуса l с центром в точке at(bt). Точки пересечения (mt и kt) окружности с проекцией ctdt являются проекциями искомых точек на пл. Т. По mt. и kt находим ms и ks, затем m и k, а по ним — m’ и k’.
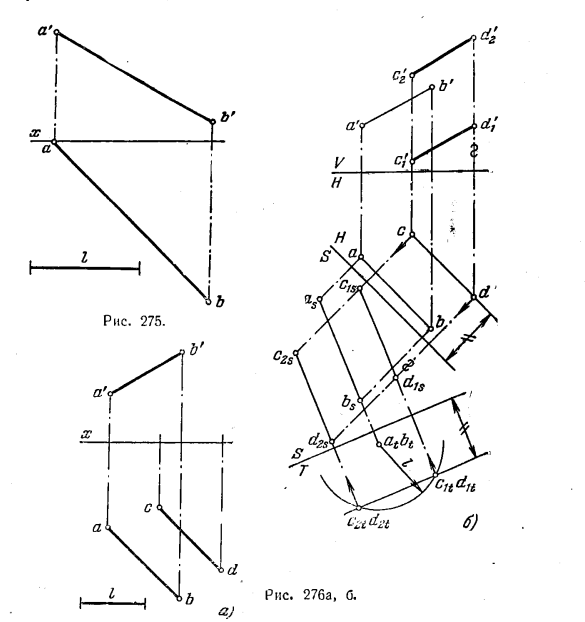
292. На прямой АВ найти точки, отстоящие от оси х на расстояние l (рис. 275).
293*. Построить недостающую проекцию прямой CD, параллельной прямой АВ, если расстояние между ними равно l (рис. 276, а).
Решение. Прямые линии, параллельные АВ и находящиеся от нее на расстоянии l, являются образующими цилиндра, осью которого служит прямая АВ, а радиусом нормального сечения — отрезок l. Исходя из этого, следует добиться того, чтобы прямая АВ оказалась перпендикулярной к некоторой плоскости: цилиндр с осью АВ изобразится на этой плоскости п виде окружности, на которой окажется соответствующая проекция прямой СD.
Построение показано на рис. 276, б. Последовательно введены дополнительные плоскости S⊥H и T⊥S, причем S||AB и Т⊥АВ Найдя точку at(bt) — проекцию АВ на пл. Т, очерчиваем дугу радиуса l. Это проекция на пл. Т цилиндра, одной из образующих которого должна быть прямая CD. Проекцией этой прямой на пл. Т
должна быть точка на проведенной дуге окружности на расстоянии от оси T/S, равном расстоянию проекции cd от оси S/Н. Получаем две точки: c1t(d1t) и c2t(d2t),
т. е. два ответа: обе прямые отвечают условиям задачи. Найдя проекции c1t(d1t) и c2t(d2t), проводим c1sd1s||asbs и c2sd2s||asbs, а затем с’1d’1||a’b’||c’2d’2.
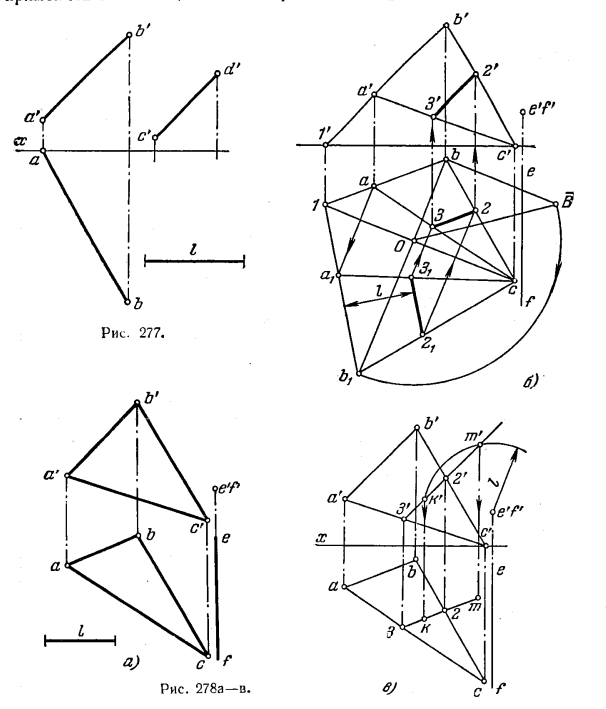
294. Построить горизонт. проекцию прямой CD, параллельной прямой АВ и отстоящей от нее на расстояние l (рис. 277).
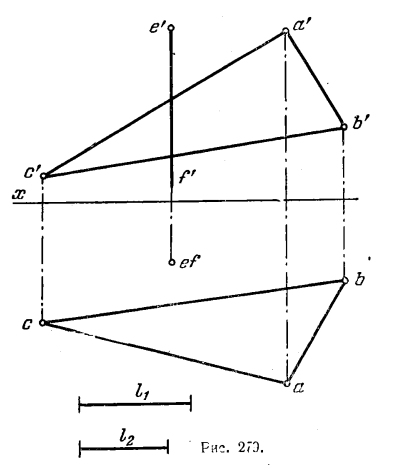
295*. В треугольнике ABC найти точку, отстоящую от прямых AВ и EF на расстояние l (рис. 278, а).
Решение. Геометрическим местом точек на плоскости треугольника, отстоящих на расстояние l от прямой АВ, является прямая, ей параллельная и проведенная от нее на расстоянии l. Таких прямых может быть две; ограничимся той, которая находится в пределах треугольника AВС. На рис. 278, б треугольник ABC повернут вокруг горизонтали до параллельности пл. H. Горизонталь проведена через точку С. Найдена натуральная величина радиуса вращения точки В — отрезок OB и положение треугольника A1B1C, когда его плоскость параллельна пл. H.
Проведя прямую 2131 параллельно на расстоянии l, находим точки 2 и 3, а по ним 2′ и 3′ на проекциях соответствующих сторон треугольника.
Переходим ко второму условию, связанному с прямой EF.
Геометрическим местом точек пространства, отстоящих от прямой EF на расстояние l, служит цилиндрическая поверхность с осью EF и радиусом l. Точка пересечения этой поверхности с прямой 2—3 является искомой точкой. Таких точек может быть две. Но в пределах данного треугольника, как это следует из рассмотрения рис. 278, в, получится лишь одна точка — точка К.
Так как EF ⊥ V, то получаем непосредственно фронт. след цилиндрической поверхности в виде дуги окружности с центром e'(f’) и радиусом l. В пересечении этой дуги с проекцией 2’3′ получается точка k’— фронт. проекция искомой точки, отстоящей от АВ и от EF на расстояние l.
На рис. 278, в показана также точка М, отвечающая условиям задачи о равноудаленности от АВ и EF (на д). Точка М находится в плоскости, заданной треугольником ABC, но вне его пределов. В условии же задачи сказано; «В данном треугольнике…». Поэтому полностью отвечает условиям задачи только точка К.
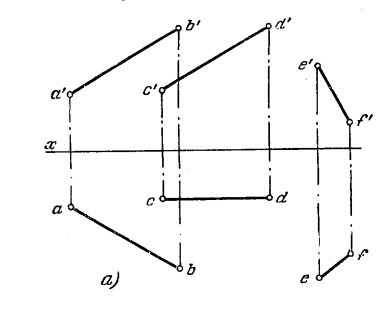
296. В данном треугольнике ABC найти точку, отстоящую от прямой АВ на расстояние l1 а от прямой EF на расстояние l2 (рис. 279).
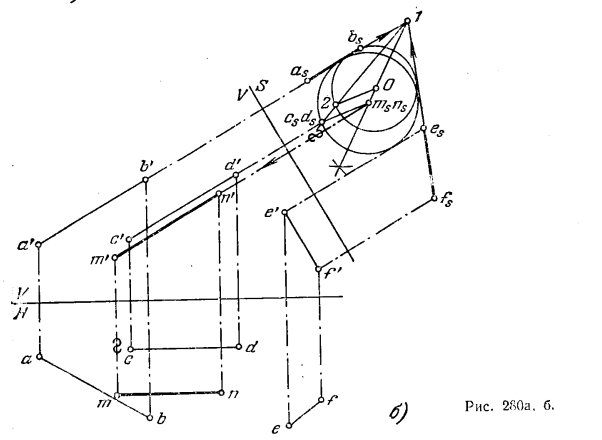
297.* Провести прямую MN, равноудаленную от прямых AB, CD и EF и параллельную одной из них,а именно прямой CD (рис. 280, а)
Решение. Представим себе, что прямая CD расположена перпендикулярно к некоторой плоскости проекций; тогда каждая прямая, параллельная CD, также будет перпендикулярна к этой плоскости, в том числе и искомая. В данном случае прямая CD параллельна пл. V; поэтому можно сразу ввести плоскость S, перпендикулярную к прямой CD, взяв ось S/V⊥c’d’ (рис. 280, б). Построим проекции asbs, cs(ds) и esfs. Проекция искомой прямой MN на пл. S представляет собой точку ms(ns), равноудаленную от прямых asbs, и esfs и точки cs(ds), т. е. является центром окружности,
проходящей через точку cs(ds) и касающейся прямых asbs и esfs. Для ее построения проводим биссектрису угла as1fs и через какую-либо точку о на ней проводим окружность, касающуюся этих прямых. Соединяем точки 1 и cs(ds) прямой линией и находим точку 2 пересечения ее с проведенной окружностью. Теперь проводим прямую через точки О и 2. Искомая точка ms(ns) лежит на пересечении упомянутой выше биссектрисы с прямой, параллельной прямой 2—О и проходящей через точку cs(ds). По проекции ms(ns) находим m’n'(||c’d’) и mn||cd.
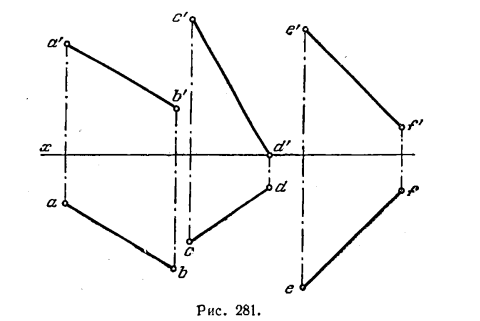
298. Провести прямую MN, равноудаленную от прямых АВ, CD и EF и параллельную прямой CD (рис. 281).
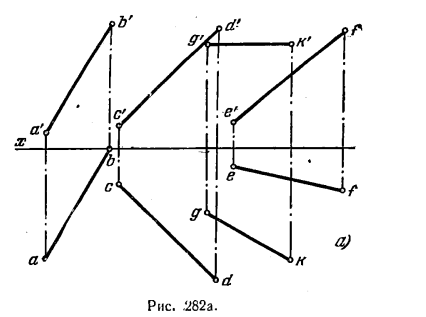
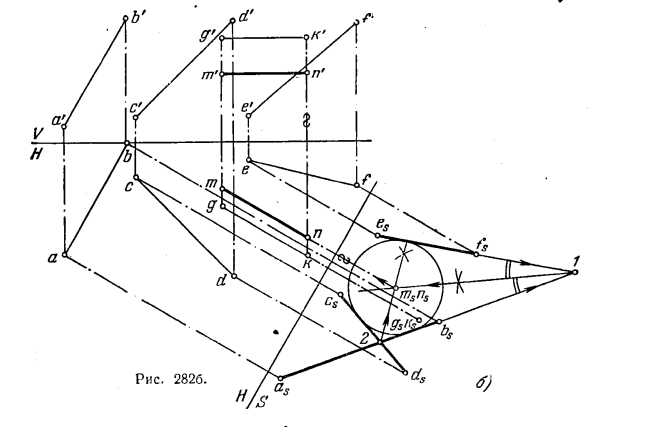
299*. Провести прямую MN, равноудаленную от прямых АВ, CD и EF и параллельную прямой GK (рис. 282, а).
Решение. И в этой задаче, очевидно, надо сделать так, чтобы прямая CD, а следовательно, и искомая параллельная ей прямая MN оказались перпендикулярными к некоторой плоскости проекций. Так как по заданию GK параллельно пл. Н, то сразу можно ввести пл. S (рис. 282, б), перпендикулярную к пл. H и к GK.
Теперь строим проекции asbs, csds и esfs. Проекция искомой прямой на ил. S должна быть точкой. Очевидно, надо отыскать точки, равноудаленные от проекций asbs, csds и esfs. Проведя биссектрисы углов as1es и cs2bs, получим в их пересечении
точку ms(ns). Это и будет проекция на пл. S искомой прямой, находящейся на равных расстояниях от АВ, CD и EF и параллельной прямой GK
Здесь дано одно из четырех возможных решений.
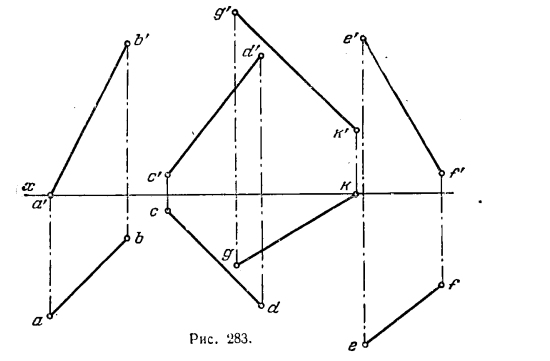
300. Провести прямую MN, равноудаленную от прямых АВ, CD и EF и параллельную прямой GK (рис. 283).
Указание. В задаче 300, для того чтобы прямая GK оказалась перпендикулярной к некоторой плоскости проекций, требуется введение двух дополнительных плоскостей.
301*. Провести прямую, равноудаленную от четырех заданных точек А, В, С и D (рис. 284, а).
Решение. Представляя себе пространственную картину, можно заключить, что искомая прямая является осью цилиндрической поверхности, образующие которой проходят через заданные точки (рис. 284, б).
Для построения этой поверхности проведем через любые две заданные точки, например А и В, прямую и примем ее за образующую цилиндрической поверхности. Теперь проведем пл. Т перпендикулярно к прямой АВ и найдем проекции at(bt), ct, dt. Проекция цилиндрической поверхности на пл. Т является окружностью, проходящей через точки сt, dt и at(bt). Центр этой окружности — точка mt(nt) — является проекцией искомой прямой.
Построение показано на рис. 284, в. Вводим пл. S⊥H и ||АВ, а затем пл. Т, перпендикулярную к пл. S и к АВ. Построив проекцию at(bt), ct и dt, находим mt — проекцию одной из точек (М) искомой прямой MN.
Затем находим ms, m и m’. Проводим m’n’||a’b’ и mn||ab.
Можно было бы соединить точки A и С, А и D, В и С, В и D, С и D и получить еще пять решений.
302. Провести прямую MN, равноудаленную от четырех заданных точек А, В, С и D (см. рис. 284, а). Дать два варианта решения: a) MN||BD и б) MN||AC.
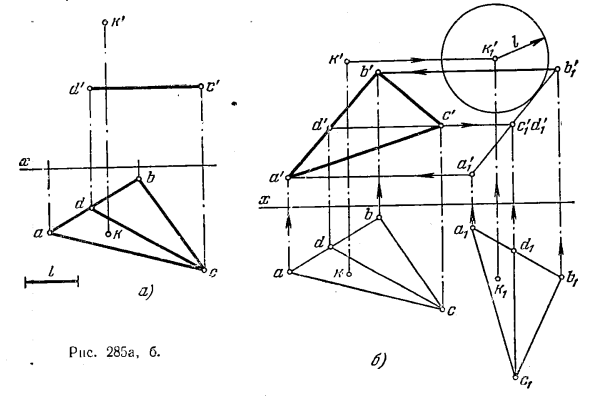
303*. Построить фронт. проекцию треугольника ABC, если даны его горизонт. проекция abc и горизонталь DC, а также известно расстояние l от точки К до плоскости этого треугольника (рис. 285, а).
Решение. Если представить себе сферу радиуса l как геометрическое место точек, удаленных на расстояние l от точки К, то искомая плоскость будет одной из плоскостей, касательных к этой сфере. При этом, если плоскость окажется фронтально-проецирующей, то ее фронт. след будет касательной прямой к фронт. проекции сферы — окружности радиуса l, и фронт. проекция треугольника ABC совпадет с этой касательной.
Поэтому преобразуем заданный чертеж так, чтобы плоскость треугольника ABC стала фронтально-проецирующей. Для этого применим поворот треугольника и точки К вокруг оси, перпендикулярной к пл. Н, но положение этой оси не покажем (способ параллельного перемещения). При таком повороте (рис. 285, б) горизонт. проекция в целом лишь изменит положение относительно оси х. А чтобы
плоскость треугольника ABC стала фронталыго-проецирующей, надо горизонталь DC расположить перпендикулярно к пл. V, т. е. проекцию dc вывести в положение d1c1 ⊥ оси х.
Теперь, очертив из точки k1 окружность радиуса l, мы можем провести через точку c’1 (d’1) касательную к окружности. На рис. 285, б проведена одна касательная, хотя можно провести еще одну, т. е. дать второе решение. Но так как методика построения не изменяется, то ограничиваемся одним решением, принимая в качестве фронт. проекции треугольника отрезок a’1b’1 . Точки a’1 и b’1 определяются по точкам a1 и b1.
В заключение остается возвратиться к заданным проекциям abc, k и k’, и получить проекции а’ и b’, исходя из построенных проекций a’1 и b’1 т. е. получить фронт- проекцию а’b’с’.
304. Построить горизонт. проекцию треугольника ABC, если даны его фронт. проекция а’b’с’ и фронталь AD, а также известно расстояние l от точки К до плоскости этого треугольника (рис. 286).
Дать оба решения.
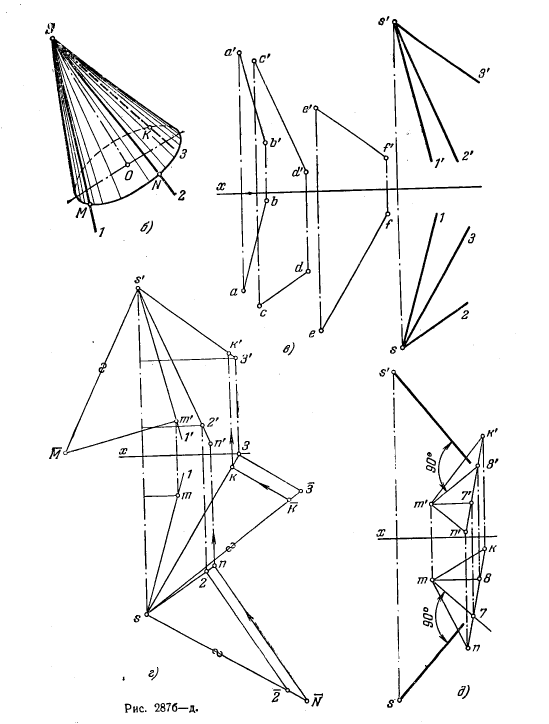
305*. Через точку S провести прямую, равнонаклоненную к заданным прямым АВ, CD и EF (рис. 287, а).
Решение. Искомая прямая является осью конуса с вершиной S, три образующих которого параллельны соответственно прямым АВ, CD и EF (рис. 287, б).
Через s’ и s (рис. 287, в) проводим проекции прямых, параллельных данным прямым (например, s’1’||a’b’, s— l||ab, s’2’||c’d’ и т. д.).
Взяв на прямой S—1 некоторый отрезок SM (рис 287, г), откладываем на двух других прямых отрезки SK=SN=SM.
Точки К, М и N задают (рис. 287, б) сечение конуса плоскостью, перпендикулярной к его оси.
Получив точки k, k’; m, m’; n, n’, строим треугольники kmn и k’m’n’— проекции треугольника KMN, в плоскости которого надо найти точку, равноудаленную от точек К, М и N, т. е. центр окружности, описанной вокруг этого треугольника. Проведя через эту точку и через точку S прямую, можно получить требуемый ответ. Но достаточно будет только провести перпендикуляр из точки S на плоскость, определяемую треугольником KMN, что и сделано на рис. 287, д при помощи горизонтали М—7 и фронтали M—8.
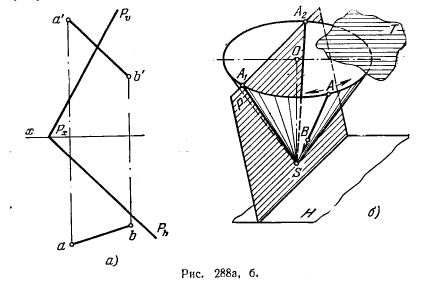
306*. Ввести прямую АВ в пл. Р вращением вокруг оси, перпендикулярной к пл. Н (рис. 288, а).
Решение. Если найти точку пересечения прямой АВ с пл. Р, то останется повернуть только одну точку прямой так, чтобы эта точка оказалась в пл. Р. Поэтому начинаем с того, что находим точку S пересечения прямой АВ с пл. Р (рис. 288, б), а далее проводим ось вращения через S перпендикулярно к пл. Н. При вращении вокруг этой оси точка S остается в пл. Р, а прямая АВ описывает коническую поверхность. Линии пересечения (SA1 и SA2) этой поверхности с пл. Р (Р проходит через вершину конуса) представляют собой искомые положения прямой АВ в пл. Р.
Построение показано на рис. 288, в. Для нахождения точки S через прямую АВ проведена фронтально-проециругощая пл. R. Точка А при повороте вокруг оси OS (рис. 288, г) описывает окружность радиуса Оа, лежащую в пл.Т, которая пересекается с пл. Р по горизонтали. Эта горизонталь пересекает окружность в точках с проекциями а1 и а’1, а2 и а’2. Проведя прямые s’a’1 и s’а’2, sa1 и sa2, находим на этих прямых положение точек b’1, b’2, b1 и b2. A1B1 и А2В2— искомые положения прямой АВ.
307. Вращением вокруг оси, перпендикулярной к пл. Н (рис. 289), совместить данную прямую АВ с а) гранью SDE.
Указание. Начать с нахождения точки пересечения АВ с соответствующей гранью.
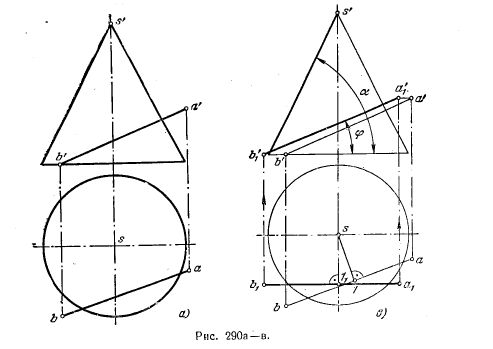
308*. Определить, можно ли прямую АВ совместить с поверхностью конуса вращения поворотом ее вокруг оси, перпендикулярной к плоскости основания конуса (рис. 290, а).
Решение. На рис. 290, б показано, что прямая АВ совпадает с поверхностью конуса вращения в том случае, если совпадет с его образующей в одном из ее положений. Это положение образующей получим, найдя точку S, пересечения прямой АВ с поверхностью конуса. Образующая S—1 определяемая точками S и S1 и есть та, с которой должна совпасть прямая АВ, если она может быть совмещена с поверхностью конуса. Но чтобы такое совмещение получилось, должны оказаться равными между собой углы, составляемые образующей конуса и данной прямой АВ с осью конуса или с прямой, проведенной через точку S1 параллельно этой оси. Так как в данном случае ось конуса перпендикулярна к пл. Н, проверку можно
свести к определению угла между АВ и пл. Н (рис. 290, в): приняв ось конуса за ось вращения для всей системы «конус и прямая», поворачиваем прямую АВ до параллельности пл. V. Так как углы α и φ не равны между собой, то прямая АВ не может быть введена на поверхность данного конуса поворотом вокруг оси, перпендикулярной к плоскости его основания.
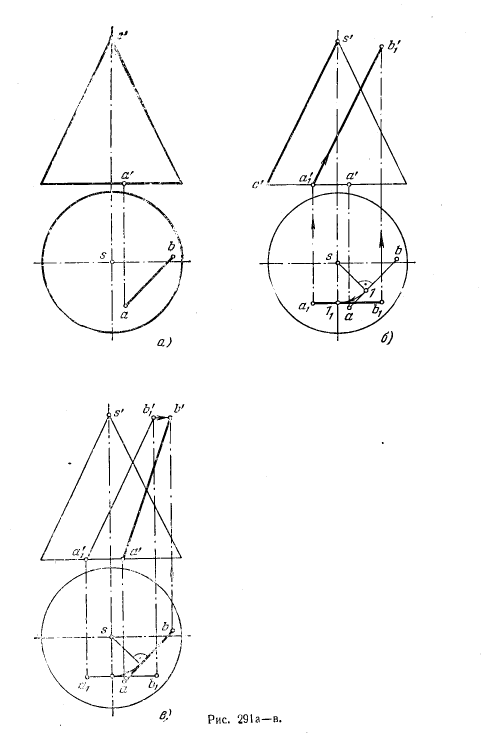
309*. Найти фронт. проекцию прямой АВ, исходя из условия, что эта прямая может быть совмещена с боковой поверхностью заданного конуса вращения поворотом вокруг оси, перпендикулярной к плоскости его основания (рис. 291, а).
Решение. Повернем систему «конус и прямая» вокруг оси конуса с тем, чтобы прямая АВ стала параллельной пл. V (рис. 291,6). Получив точку a’1 — фронт. проекцию точки А после поворота, проведем а’1b’1||s’c’, т. е. получим равные углы между осью конуса и а) его образующей, б) прямой АВ. Выводя конус и прямую в начальное положение, получим фронт. проекцию а’b’ (рис. 291, в) в соответствии с условиями задачи.
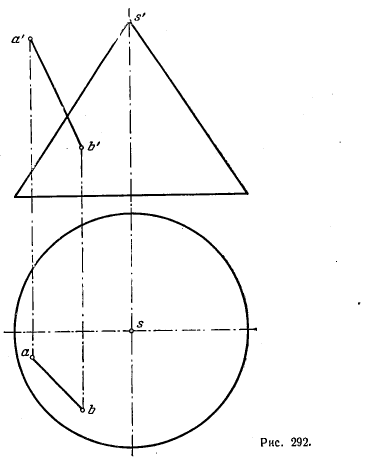
310. Ввести прямую АВ на поверхность данного конуса (рис. 292) поворотом вокруг оси, перпендикулярной к плоскости его основания.
Указание. Произведя проверку и убедившись в том, что задача может быть решена, надо найти точку пересечения прямой АВ с боковой поверхностью конуса. Эта точка вместе с вершиной конуса определяет его образующую в том ее положении, когда прямая АВ совпадает с ней.
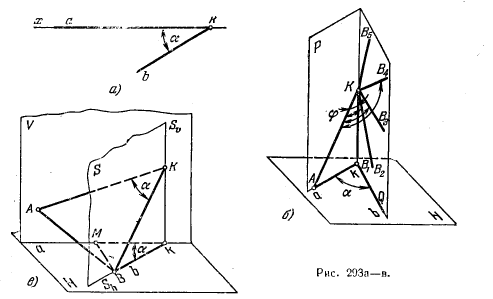
311*. Построить фронт. проекцию угла АКВ, натуральная величина которого равна его горизонт. проекции akb (рис. 293, а)
Решение. Известно, что проекция острого (или тупого) угла может равняться проецируемому углу не только в случае параллельности плоскости угла и плоскости проекций. На рис. 293, 6 показано, что, например, все углы, стороны которых соответственно расположены в пл. Р и Q, перпендикулярных к пл. H, имеют своей
горизонт. проекцией угол, равный углу akb. Очевидно, среди различных углов име-ется угол, равный этой проекции.
Далее показано построение фронт. проекции угла, равного в натуре его заданной горизонт. проекции. Сделано это тремя способами.
1. Через стороны ak и bk угла akb (рис. 293, в), лежащего в пл. H, проводим две плоскости — пл. V и горнзонтально-проецирующуга пл. S. Угол α является линейным углом двугранного, образованного этими плоскостями. Стороны угла, равного его горизонт. проекции, должны лежать — одна в пл. V, другая в пл. S. Этот угол построен при помощи треугольника АКВ, подобного некоторому треугольнику MkB, взятому на пл. H. Построение проводится так, чтобы стороны АВ и ВМ были сходственными.
Задаемся некоторым коэффициентом подобия λ. На ребре двугранного угла выбираем точку К так, чтобы BK= λ · Bk. Если теперь построить точку А с тем, чтобы АК = λ · Mk и АВ= λ · ВМ, то треугольники АКВ и MkB окажутся подобными, и угол АКВ будет равен α.
Для построения точки А используем два геометрических места точек: геометрическое место точек в пл. V, удаленных от точки K на расстояние AK = λ · Mk (т. е. окружность, проведенная из точки К радиусом λ · Mk), и геометрическое место точек, отстоящих от точки В на расстояние АВ=λ · ВМ.(т. е. сфера радиуса АВ с центром в точке В). Точка А должна лежать в пл. V, т. е. должна быть на окружности, по которой пл. V пересекает указанную сферу и центром которой является фронт. проекция точки В.
В пересечении обеих окружностей, расположенных в пл. V, получаем две точки, из которых на рис. 293, я показана одна — точка А.
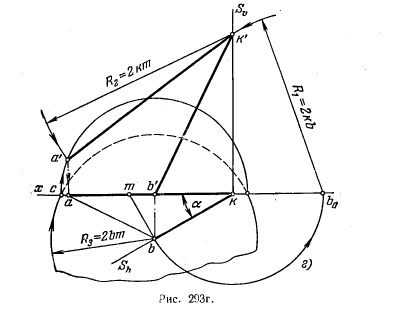
Соответствующий чертеж приведен на рис. 293, г. Принимаем λ = 2. Из точки b0 (построение ее ясно из чертежа) проводим дугу радиуса R1 = 2kb до пересечения в точ
ке k’ с линией связи, проходящей через точку k. Из точки k’ проводим дугу радиуса R2 = 2km. Если теперь из точки b радиусом R3 = 2bm провести окружность, то получим проекцию упомянутой выше сферы.
Окружность, по которой эта сфера пересекается плоскостью V, имеет центр в точке b’ и радиус, равный cb’. Точка а’ лежит на пересечении дуг радиуса R2 и радиуса, равного cb’, точка а — на оси х. Угол а’k’b’— искомая фронт. проекция угла, равного своей горизонт. проекции.
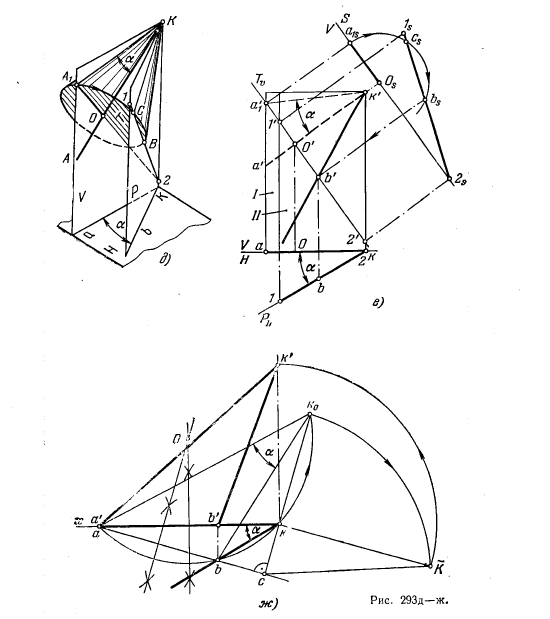
2. Возьмем точку k (рис. 293, д) на ребре двугранного угла, образованного плоскостями V и Р, проведенными через стороны ак и bk угла akb. Из этой точки проведем в пл. V прямые АК и А1К, образующие между собой угол, равный α1 и повернем прямую А1К вокруг прямой АК. При этом образуется коническая поверхность с образующей А1К и осью АК. Линия КВ пересечения конической поверхности плоскостью Р будет стороной угла АКВ, в натуре равного α. Чтобы найти эту линию пересечения, надо построить прямую 1—2 пересечения пл. Р с пл. Т основания конуса. Тогда точки С и В пересечения окружности основания с прямой 1—2 определят образующие, по которым нл. Р пересекает коническую поверхность.
Чертеж показан на рис. 293, е, причем плоскости V и Р изображены прямоугольниками I и II. Через точку k’ в прямоугольнике I проведены прямые a’k’ и a’1k’ так, чтобы угол между ними был равен α. Через точку а’1 перпендикулярно к a’k’ проведен след Tϑ плоскости Т — основания конуса. Точка О’О — центр окружности основания конуса. Прямая с проекциями 1’2′ и 1—2 — линия пересечения плоскостей Т и Р.
Введя дополнительную пл. S ⊥ V и ⊥ АК, построим проекции Os и а1s, а также Is2s. Окружность, проведенная из точки os радиусом osа1s, пересекает прямую Is2s в точках cs и bs— проекциях точек, принадлежащих образующим КВ и КС. На рис. 293, е показано построение фронт. проекции только точки В: по точке bs построена точка b’. Угол a’k’b’ является фронт. проекцией угла, в натуре равного углу α.
3. В этом случае использовано совмещение плоскости искомого угла с пл. H (рис. 293, ж).
Проводим прямую ab — горизонт. след плоскости, в которой лежит рассматриваемый угол, и поворачиваем вокруг него точку К до совмещения ее с пл. Н. Чтобы
при этом угол аК0b оказался равным α, надо вписать угол аК0b в окружность, проведенную через точки а, b и k. Тогда углы akb и аК0b, как вписанные, опирающиеся на
одну и ту же дугу, будут равны между собою. Остается найти точку К0 в пересечении окружности, проведенной через точки а, b и k, со следом плоскости вращения точки К вокруг прямой ab. Зная натуральную величину сK радиуса вращения точки К
и его горизонт. проекцию ck, находим отрезок kK — превышение точки К над пл. H, а это дает нам возможность получить точку k’. Угол a k’b’ является искомой фронт. проекцией угла АКВ, равного своей горизонт. проекции. Во всех примерах мы ограничились показом построения лишь одного угла, хотя углов, натуральная величина которых равна заданной горизонт. проекции, множество.
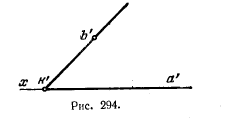
312. Построить горизонт. проекцию угла АКВ, равного в натуре своей фронт. проекции a’k’b’ (рис.294).
Решить всеми тремя способами.
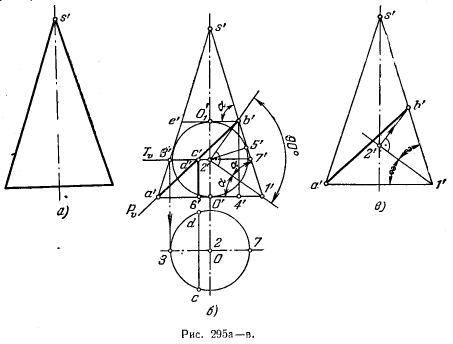
313*. Найти направление фронт. следа фронтально-проецирующей плоскости, пересекающей заданный конус вращения так, чтобы профильная проекция эллипса сечения оказалась окружностью (рис. 295, а).
Решение. В общем случае профильная проекция эллипса, получаемого при пересечении конуса вращения, представленного на рис. 295, а, фронтально-
проецирующей плоскостью Р, является эллипсом (рис. 295, б), оси которого равны величинам отрезков b’4′ и cd.
Если окажется, что b’4′ = cd, то эллипс сечения изобразится на пл. W окружностью. Этого можно достичь, если след Рϑ искомой плоскости направить по диагонали равнобочной трапеции а’е’b’1′ (рис. 295, б), в которую вписывается окружность с центром в точке 2′. Для построения такой трапеции проводим биссектрису угла а’1’b’ до пересечения с осью симметрии трапеции в точке 2′. Проводим из этой точки перпендикуляр к биссектрисе и находим точку b’ (рис. 295, в).
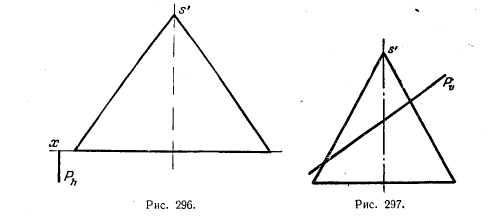
314. Дан след Ph фронтально-проецирующей пл. Р, пересекающей конус вращения по эллипсу. Построить фронт. след этой плоскости из условия, что профильная проекция эллипса является окружностью (рис. 296).
315. Будет ли (рис. 297) проецироваться на пл. W в виде окружности эллипс, получаемый при пересечении данного конуса вращения фронтально-проецирующей пл. Р?
Интересная комплексная задача по начертательной геометрии
Условие задачи
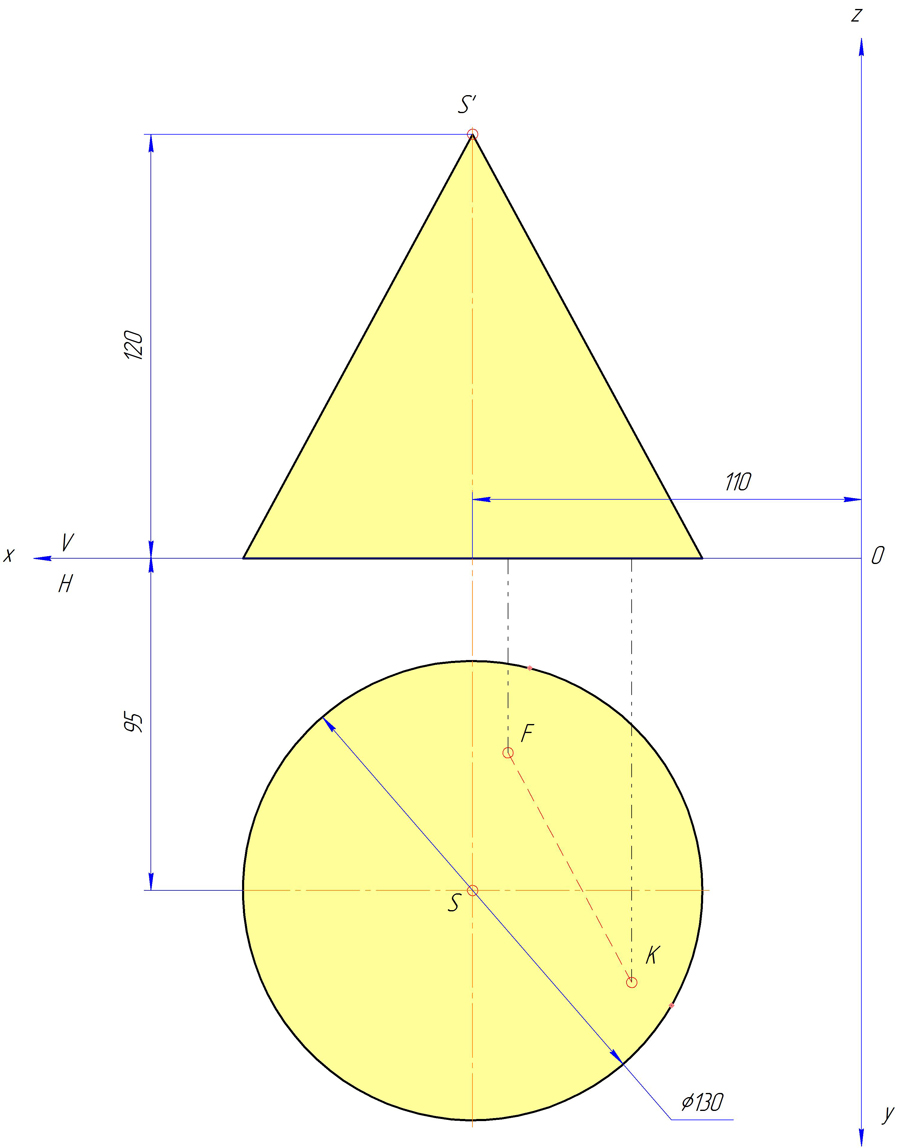
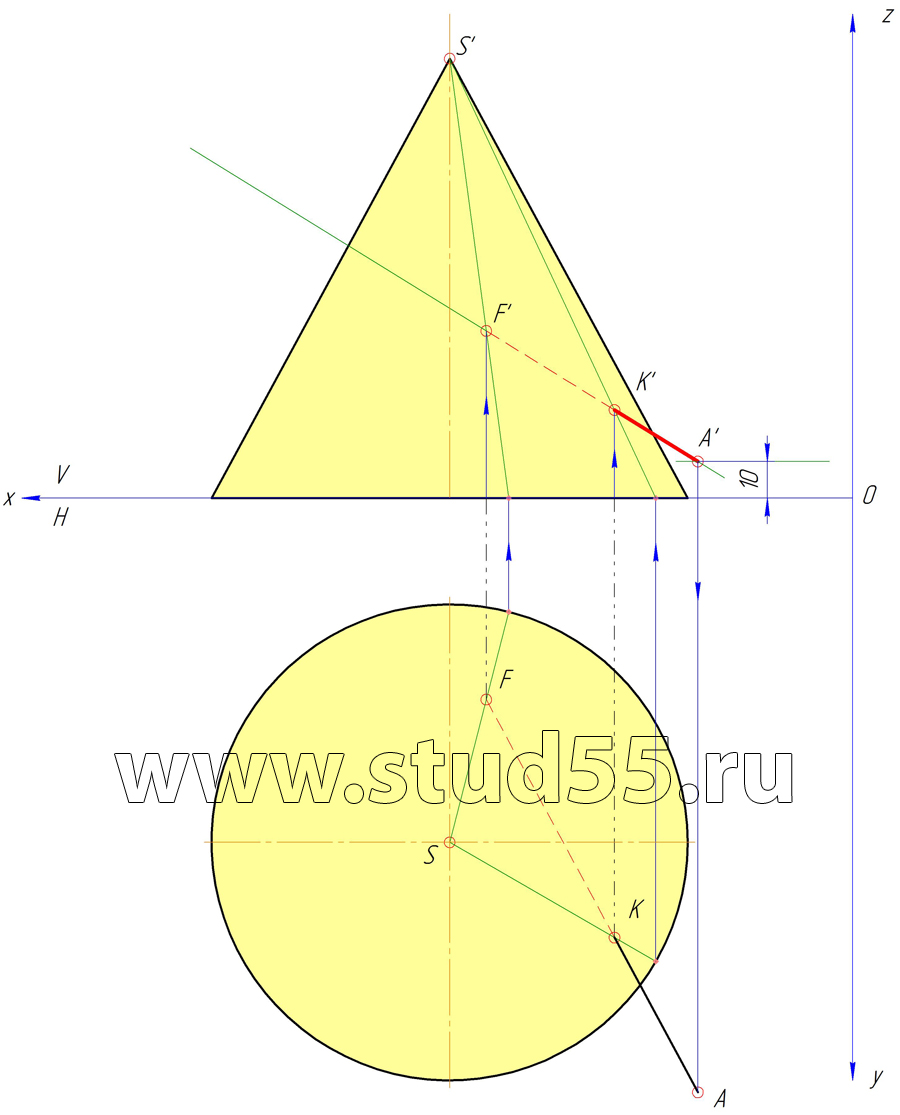
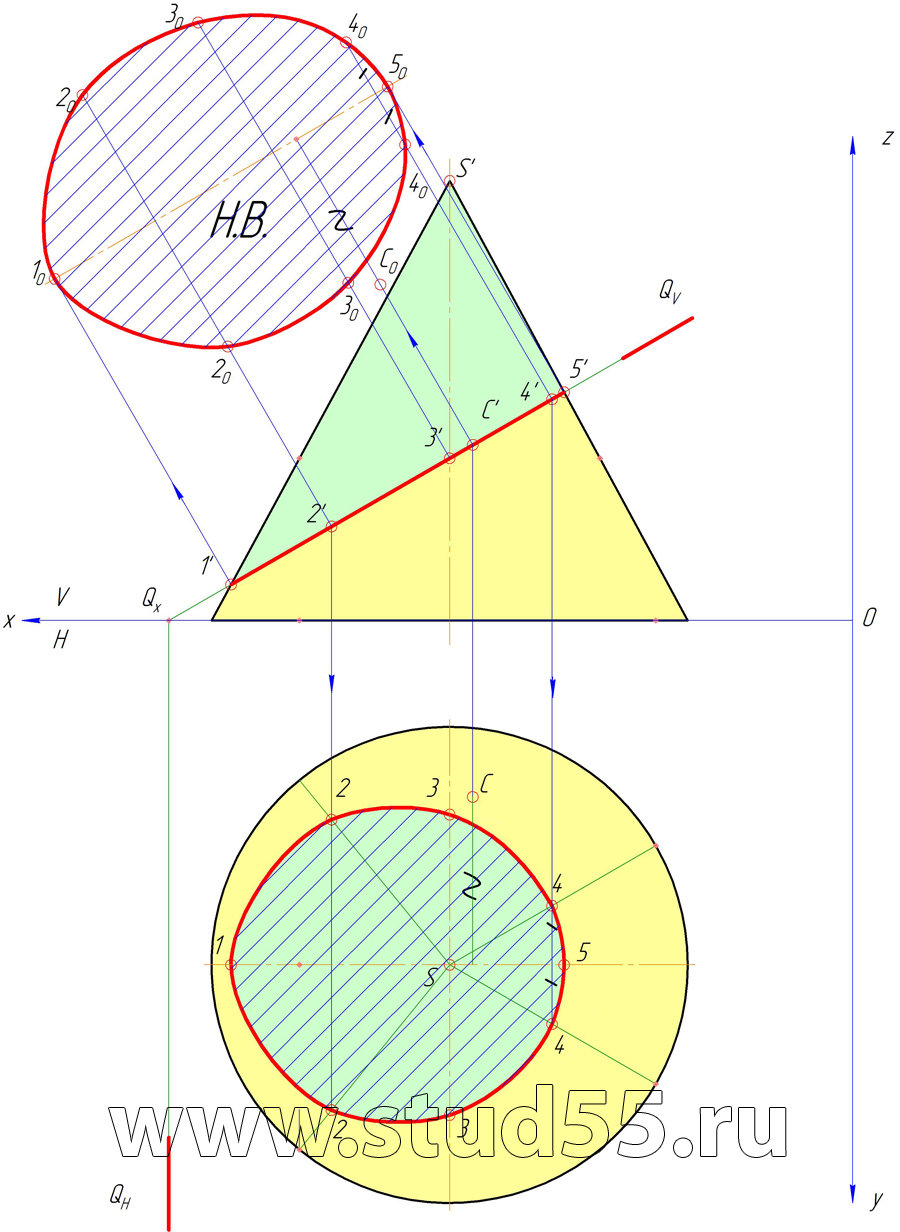
Прямой круговой конус с основанием на плоскости H (диаметр основания 130 мм) и вершиной в точке S (110;95;120) пересекаются плоскостью Q и прямой AB, заданной горизонтальными проекциями точек пересечения её с поверхностью конуса: F (100;55;-) и К (65;120;-). Длина прямой АВ равна 200 мм. Точка А находится на расстоянии 10 мм от плоскости Н.
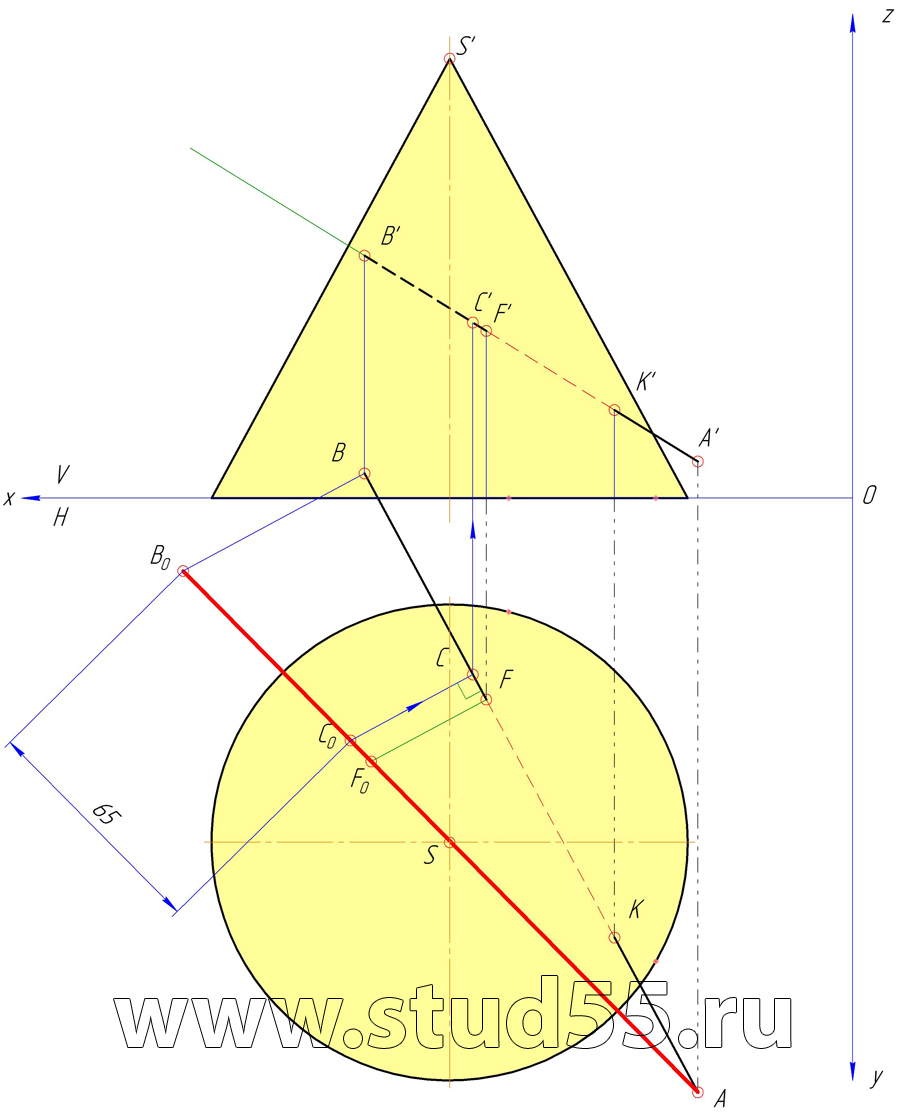
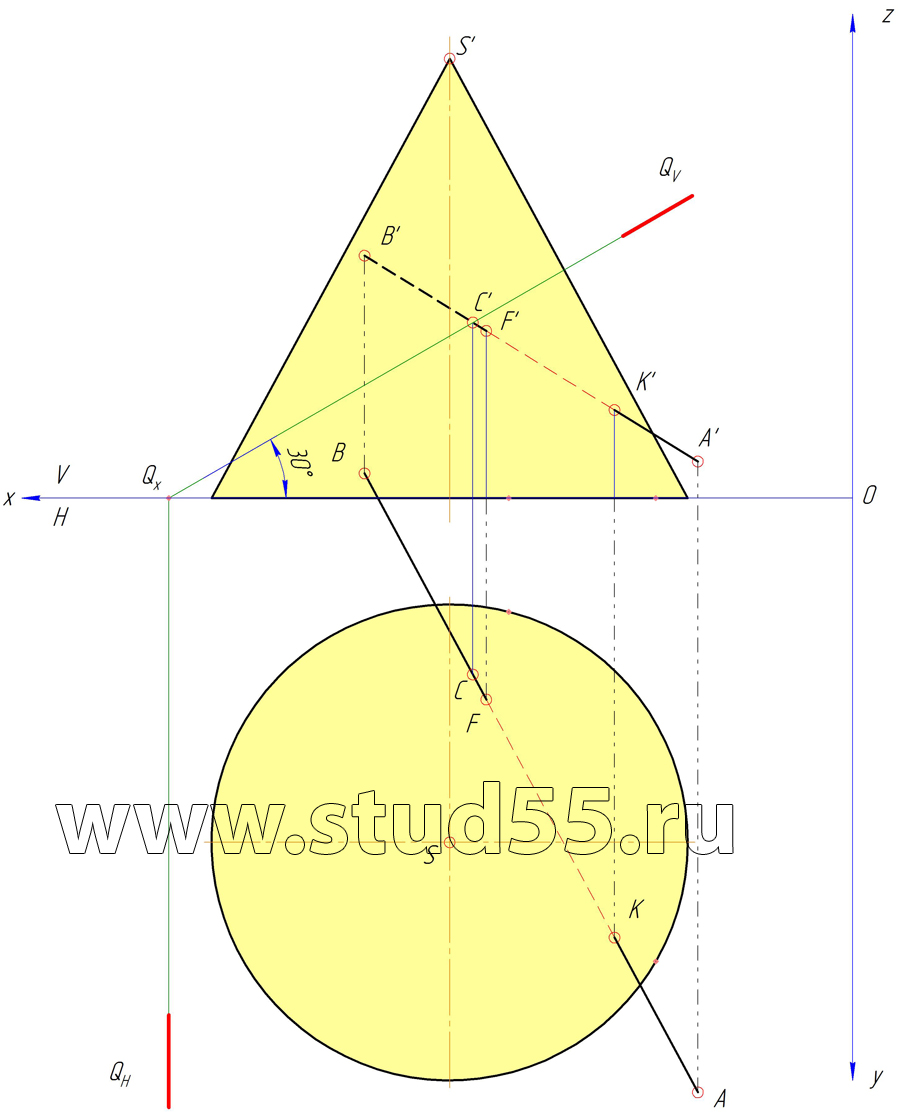
Плоскость Q наклонена к горизонтальной плоскости проекций под углом равным 30 гр. и пересекает АВ в точке С, если ВС=65 мм.
Определить
1) недостающие проекции точек F и K;
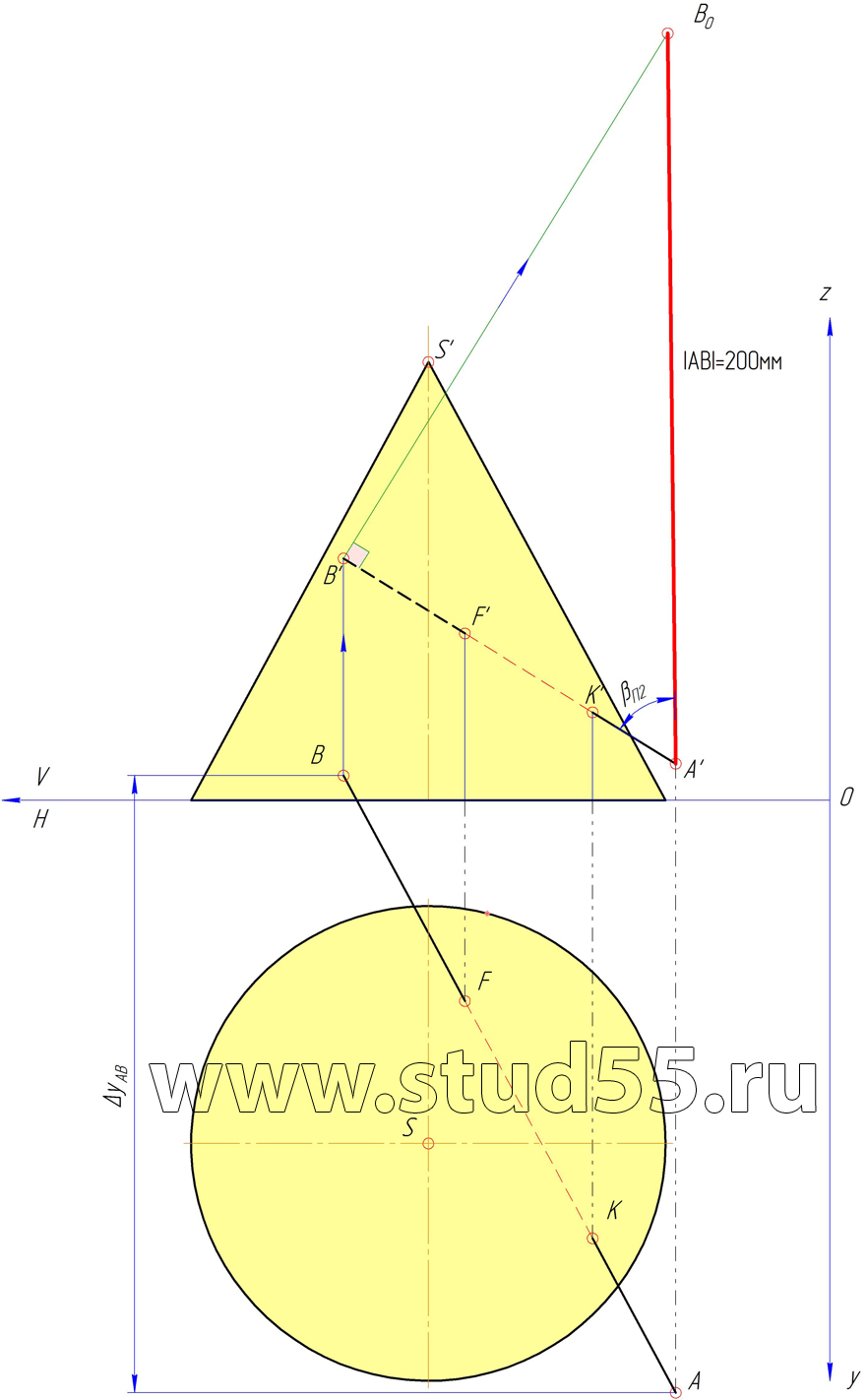
2) проекции прямой АВ и углы наклона её к фронтальной и горизонтальной плоскостям проекций;
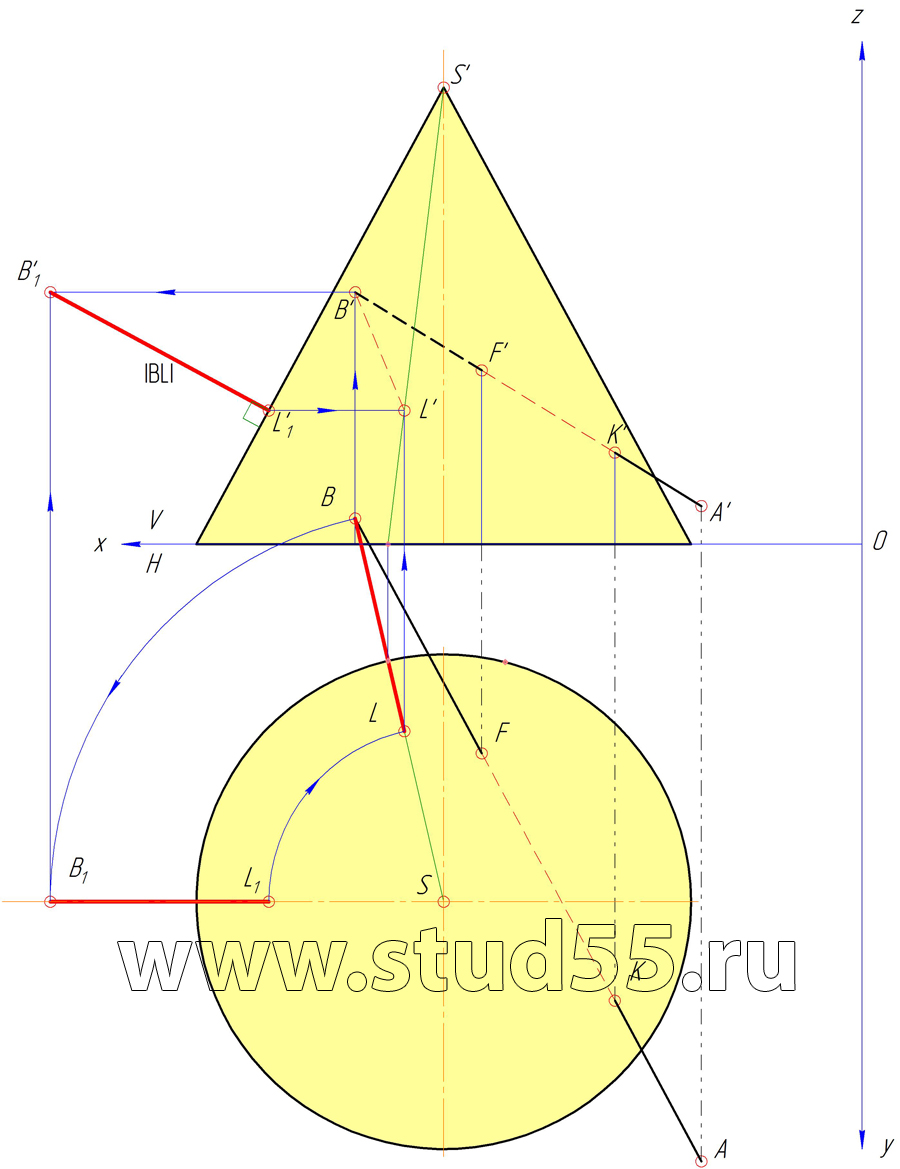
3) расстояние от точки В до поверхности конуса;
Построить
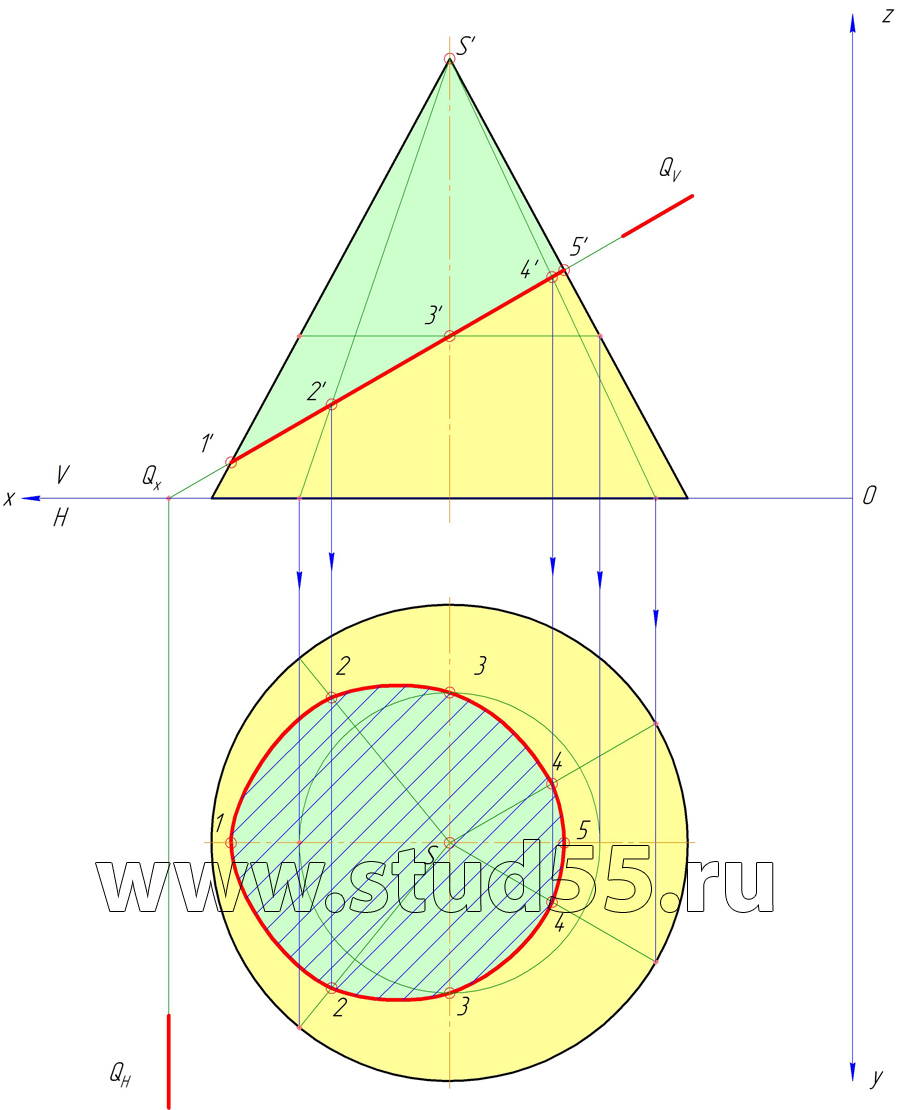
1) проекции линии пересечения конуса и плоскости Q;
2) натуральную величину фигуры сечения с указанием точки пересечения плоскости Q и прямой АВ.
Пошаговое решение
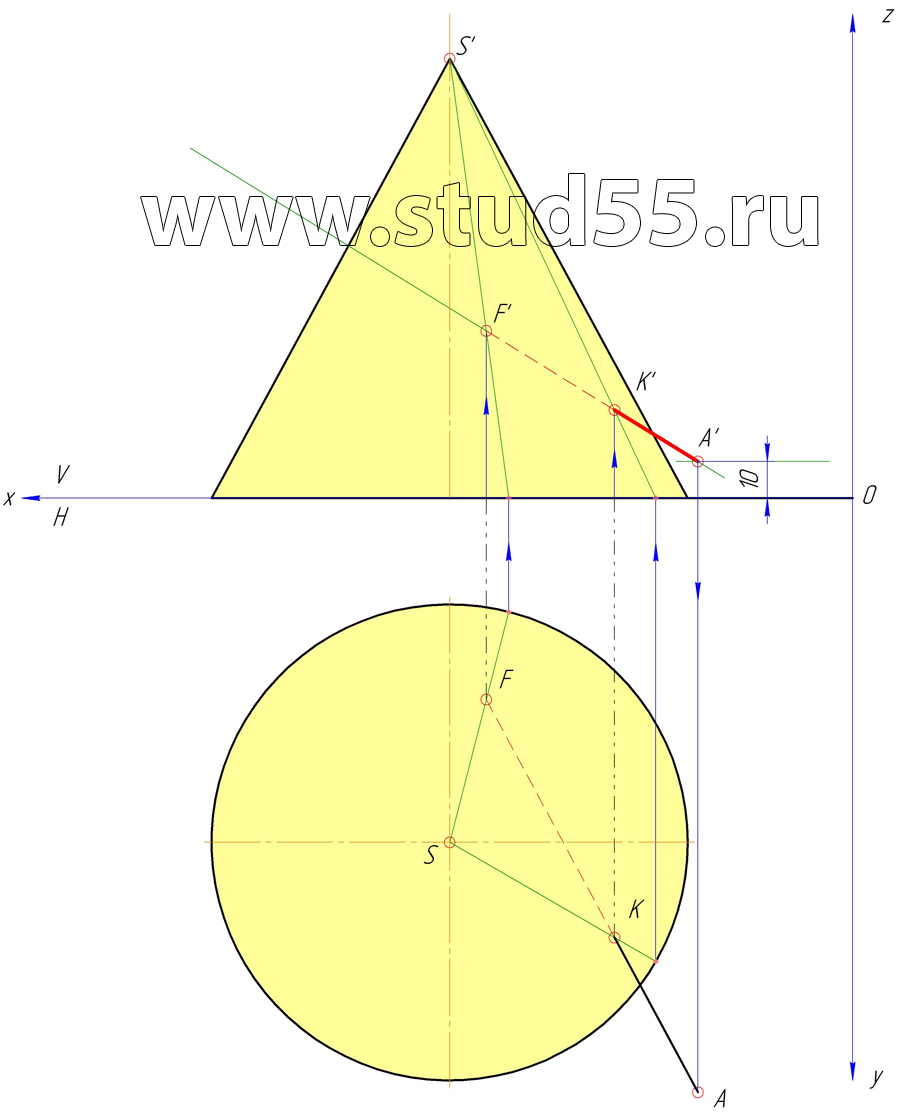
Шаг №1 — Построение конуса по координате вершины и заданной высоте 120 мм, и горизонтальных проекций точек F и К по заданным координатам
Шаг №2 — Построение точек F и K на вертикальной плоскости проекций V
Шаг №3 — Нахождение проекций точки А
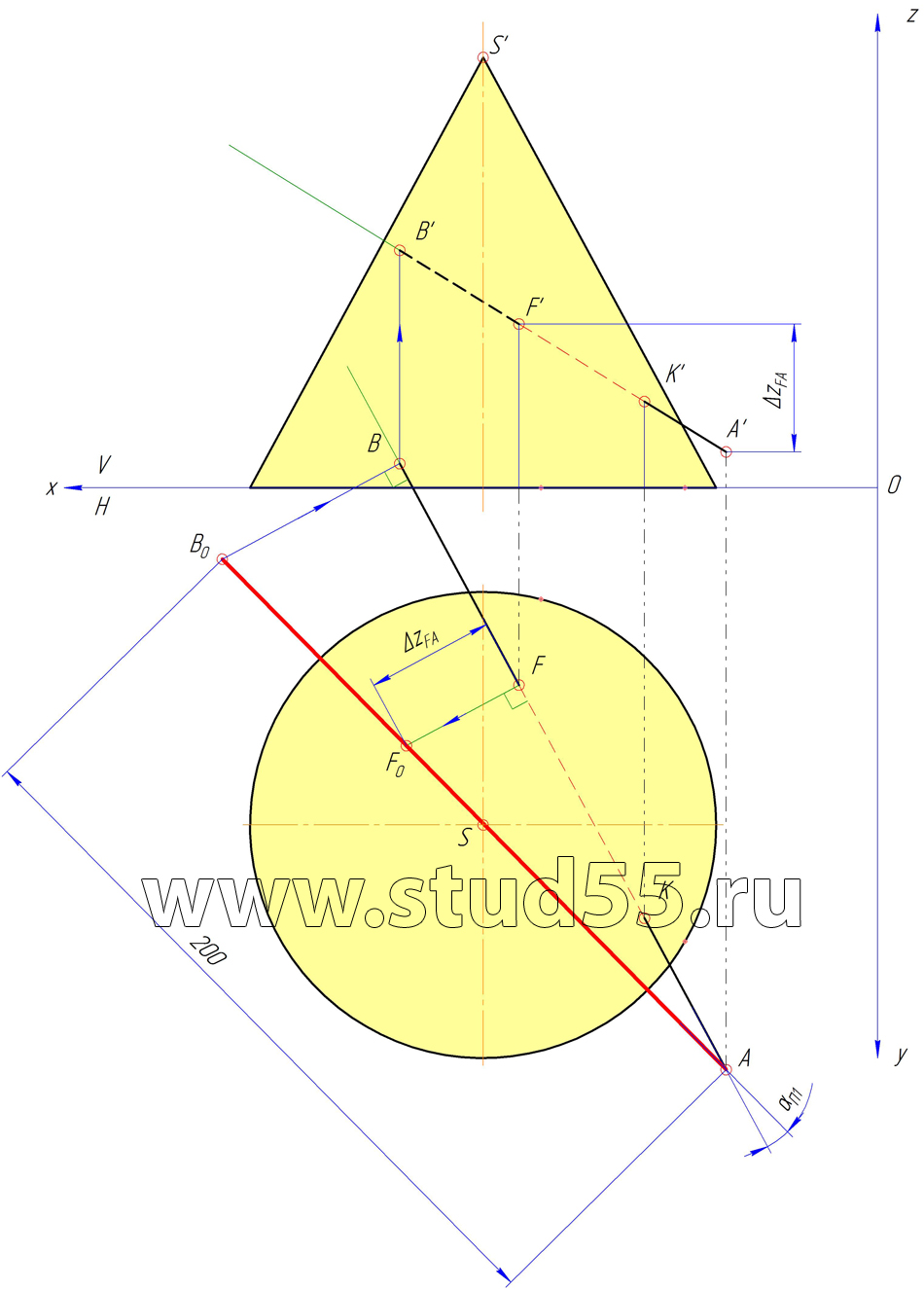
Шаг №4 — Нахождение проекций точки В и угла наклона АВ к плоскости Н
Шаг №5 — Нахождение угла наклона АВ к плоскости V
Шаг №6 — Нахождение расстояния от точки В до поверхности конуса
Шаг №7 — Нахождение проекций точки С
Шаг №8 — Построение плоскости Q
Шаг №9 — Построение сечения конуса плоскостью Q в горизонтальной плоскости
Шаг №10 — Построение натуральной величины фигуры сечения
Раздел: Без рубрики /
- Рекомендуем
- Комментарии
- Наши товары

8.3. ПЕРЕСЕЧЕНИЕ ПРЯМОЙ
СПОВЕРХНОСТЬЮ ВРАЩЕНИЯ
Точками пересечения прямой с поверхностью вращения являются точки пересечения этой прямой с контуром сечения поверхности вспомогательной плоскостью, проведенной через эту прямую (рис. 8.14).
а)
б)
Рис. 8.14. Пересечение прямой линии с поверхностью: а) модель; б) эпюр
В общем случае, алгоритм решения задачи построения точек пересечения прямой с поверхностью вращения состоит в следующем:
1. Провести плоскость частного положения α через прямую l. Вспомогательная секущая плоскость должна пересекать поверхность по линии, проекции которой можно легко построить – по окружности или прямой.
159

2.Построить линию сечения поверхности плоскостью α.
3.Определить точки пересечения прямой l с линией сечения – точки А и В.
4.Обвести чертеж прямой с учетом видимости точек пересечения. Видимую линию обводят толстой основной линией, невидимую – тонкой штриховой, а внутри между точками входа и выхода – сплошной тонкой линией (считается, что линия отсутствует).
Построение значительно упрощается, если:
– прямая является проецирующей (рис. 8.15, а). Вырожденная проекция прямой (точка) обладает собирательным свойством. Поэтому вырожденная проекция прямой совпадает с проекциями точек пересечения прямой с поверхностью вращения. Другие проекции точек пересечения определяются при помощи построения параллелей. На примере, вырож-
денная проекция прямой l3 совпадает с А3 и В3. На плоскости П1 проекции А1 и В1 строятся при помощи параллели (окружности), на П2 – по линии связи;
– поверхностью вращения является цилиндр (рис. 8.15, б). Вырожденная проекция цилиндра (окружность) обладает собирательным свойством. Поэтому проекции точек пересечения прямой с поверхностью лежат на вырожденной проекции цилиндра. Другие проекции точек пересечения определяются по линии связи. На примере, вырожденная про-
екция цилиндра находится на П3. Пересечение прямой и вырожденной проекции определяют проекции А3 и В3. На плоскости П2 и П1 проекции точек А и В строятся по линии связи.
а) б)
Рис. 8.15. Пересечение: а) проецирующей прямой с тором; б) прямой с цилиндром
160

Задача 1.
Построить пересечение прямой l с поверхностью сферы: Дано: Решение:
161

Задача 2.
Построить пересечение прямой l с поверхностью конуса: Дано: Решение:
162

Дано:
Дано:
Задача 3.
Построить пересечение прямой l с поверхностью тора:
Решение:
Решение:
164

Дано:
Дано:
Задача 4.
Построить пересечение прямой l с поверхностью цилиндра:
Решение:
Решение:
165

8.4. ОПРЕДЕЛЕНИЕ РАССТОЯНИЯ ОТ ТОЧКИ ДО ПОВЕРХНОСТИ
Расстоянием от точки A до поверхности вращения является расстояние от точки A до образующей поверхности вращения, которая лежит в плоскости , заданной данной точкой A и осью i поверхности вращения.
Для определения натуральной величины расстояния от точки A до поверхности вращения необходимо выполнить следующие преобразова-
ния (рис.8.16):
1.Вращением точки A вокруг оси i вывести точку A в плоскость ‘, параллельную плоскости проекций (на одной плоскости проекций проекция точки A движется по окружности, а на другой плоскости проекций проекция точки A перемещается по линии, параллельной смежной плоскости проекций).
2.После такого преобразования, из точки A’ опустить перпендикуляр к контурной образующей поверхности вращения до пересечения в точке В’. Отрезок перпендикуляра A’В’ – натуральная величина расстояния от точки до поверхности вращения.
3.Чтобы найти точку В, необходимо выполнить обратное преобра-
зование – вращение плоскости ‘ со всеми точками в исходное положение.
Рис. 8.16. Определение расстояния от точка до поверхности вращения
Рассмотрим решение задач по изучаемой теме.
166

Задача 1.
Определить расстояние от точки А до поверхности сферы: Дано: Решение:
Задача 2.
Определить расстояние от точки А до поверхности цилиндра: Дано: Решение:
167

Задача 3.
Определить расстояние от точки А до поверхности конуса: Дано: Решение:
Задача 4.
Определить расстояние от точки А до поверхности тора: Дано: Решение:
168
Владикавказский математический журнал Октьябрь-декабрь, 1999, Том 1, Выпуск 4
УДК 517.982
РАССТОЯНИЕ ОТ ТОЧКИ ДО КОНУСА В ГИЛЬБЕРТОВОМ ПРОСТРАНСТВЕ
В. Т. Худалов
В этой статье установлены явные формулы расстояния от точки до произвольного круглого конуса в гильбертовом пространстве [1]. В [2] эти формулы были получены лишь для частного случая регулярного круглого конуса в терминах метрически положительной и метрически отрицательной частей элемента. В качестве приложения дано решение одной экстремальной задачи в пространстве непрерывных функций.
1°. Пусть К(еі,а) — круглый конус в гильбертовом пространстве Н с оротонор-мированным базисом г і. г….где а – произвольное число, а Є (0,1), т. е.
К(еі,а) = = (хі,х2, • • • ,хп,…) : (ж, еЛ) > а||ж||| =
= їх Є Н : х ^ а( ^х], | > = < х Є Н : х 5= 0, х 5= а2 ^
^ к=1 ‘ ‘ ^ п=1
СЮ
2
а оо 2 і _
= < х = (хг,х2, • • • ,хп,…) : х
где (5 = а2. Согласно теореме 2.1.5
К*(еі, а) = К(еі, /і — а2) = і х : х 5= —,
I Л
СЮ
2
п=2
Возьмем произвольный элемент X (г П.Х (Х1,Х2, ■ ■ ■) и ПОЛОЖИМ С = /5^п = 2 Хп■ Если х € К(ег,а), то ясно, что й{х,К{е,а)) = 0, и проекция х на К(ег,а) равна
Ж. р’ /у» – /у»
• «АУ |Л/ •
Если х € —К(б1, а), то имеем: х = 0 + х, где 0 € К{е, л/1 — а2), х € —К(в1, а) = -К*(еиу/1 — а2) (см. [3; теорема 3]) и по теореме Моро [3] получаем: проекция х на к(в1, /Т — а2) равна 0 и
й(х./К(е 1, /1 — а2)) = ||ж||.
Рассмотрим теперь основной случай. Пусть х ^ ±К(ег,а), тогда
1
Х < / —Х < —с. (1)
/3
© 1999 Худалов В. Т.
Будем искать представление вектора ж в виде: х = «+г>, («, г>) = 0, где и Є К(еі,а), V Є —К*(еі,а) = —К(еі, л/і — а2)- Положим
/ ж2 Хп (1 х2 Хп
и = а І /З, — І, г; = , ——>•••)•
Имеем
( л Л ж2 + ж3 + ‘ ‘ ‘ + хп + • • • і п
(«, г>) = II————————-д———— ] = 0,
і . п и А и А и
х = и + у = А/ > – .———;г2. • • •,———жп,
р с с
А/З – І = жь
А і ____________ с_
откуда получаем
Складывая уравнения, будем иметь
Л(,, + ^)-Х1 + ТУ
откуда
л х/3 + с (3(ф — х 1)
/З2 +1 ’ 1Л = /З2 + 1 ‘
При этом в силу неравенств (1)
ж 1/0 + с > 0, с/3 — XI > 0,
т. е. А, ц € Ж+ и « € К{е, а), V € —К(е 1, л/1 — а2). Следовательно, по теореме Моро имеем: проекция вектора х на К(ег,а) равна и, где
хф + с( Х2 Хп С + Ж1/3
«- ^2 + 1 (/з, с с(/32 + 1)(с/3,ж2,…,жп,…) –
(с + хф){ф — Х) С + Х1/0
= с(/32 + 1) 61 + с(/32 + 1)Ж”
Тогда
/3(с/3 – Ж1)а/1 +/32 ф — XI а{х, К{е1,а) = ||г>|| = – —
Ж/З2 + 1) ^1 + /3:
Учитывая, что
жі = (еі,ж); с = а/||ж||2 – (еьж)2,
получаем
(1(х, К(еі,а)) = р2 ^Иж112 ~ (еъж)2) – ^(еъж)^ •
Расстояние достигается на векторе
МИІ2 – (еі,ж)2 + (еі,х)Р)(Ру/\х\2 – (еьж)2 – (еьж))
и =
(1 +/32)а/||ж||2 – (еьж)2
+
+ 7ІМІ2 ~ (вьж)2 + /?(еьж)^ (1 + /32)а/||ж||2 – (еьж)2
Наконец, если ж ^ К{е,а) и ж € —К(е, л/1 — а2), то ж € —К*(е1,а) и ж = 0 + ж, проекция ж на К(ег,а) есть 0, а й(х,К(е1,а)) = ||ж||. Итак, получаем следующую формулу:
й(х, К(еі, а)) =
0,
ж
«(/1И12 – (еі,ж)2
если ж Є К(еі,а);
если ж 0 К{еиа) и ж Є —і^(еі, /і — а2); если ж ^ К(еі, а) и ж ^ (еі, л/1 — а2).
Замечание, При а = получаем формулу (4) из примера 2.1.2 в [4].
2°. Рассмотрим теперь произвольный круглый конус К (а, а), где а Є Н — произвольный вектор, ||а|| = 1 и а Є (0,1). Пусть иш — преобразование Хаусхолдера [5], переводящее вектор а в вектор е,.
Тогда иш : Н —> Н, ш = а — еі, иш — унитарный оператор, т. е. Ц~1 = Л* = иш. Согласно утверждению 1.5.2 иш переводит конус К(а, а) в конус К(еі,а).
Пусть ж Є Н — произвольный вектор. Имеем иш(а) = еі, иш(еі) = а,
, , жі —(а, ж) жі —(а, ж)
иш(х) = х + л а—–к ’ ві-
1 — О-і 1 — Оі
Так как иш — изометрия, то
й(х,К(а,а)) = й(иш(х), К(е<, а)).
Если ж Є К(а, а), то й(х,К(а,а)) = 0. Если ж £ К(а, а) и ж Є —К(а, л/1 — а2), то
иш(х) ^ К(еі, а) и ж Є ^К{е, л/1 — а2) и, значит, в этом случае
й(х ,К(а,а)) = ||ї7ш(ж)|| = ||ж||.
Если же ж ^ К (а, а) и ж ^ —К (а, л/1 — а2), то £7ш(ж) ^ і^(еі, а) и 1/ш(х) ^
-К(еі, л/Г — а2), следовательно, в силу предыдущего пункта, имеем
7/ ч ч ,( жі —(а, ж) жі —(а, ж) Д
а(ж, А (а, а)) = а ж Н———–а————-е, К (еі, а) =
1 — аі
1 — аі
= ал ж
(еьж) +
(жі — (а,ж))(аі — 1)
1 — аі
= а/||ж||2 — (а, ж)2 — /і — а2(а, ж).
/1 — а2(а, ж) =
Найдем проекцию вектора ж на конус К (а, а). Имеем
й(х,К(а,а)) = й(иш(х), К(е<, а)), т. е. проекция х ка, К (а, а) равна образу проекции вектора
, , х — (а, ж) х — (а, ж)
иш(х) = ж + Л а—–К ’ ег
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
1 — 0-1 1 — Оі
на К{е,а) при отображении 11ш. Согласно предыдущему пункту, получим
ММІ2 – (а>х)2 + (а^)тї=ї)(7ї=ї 7ІІжІІ2 – (а>х)2 – (а>хУ)
Рх =———————-, ^ ^ ——————а+
13^2 71И|2 – (а, ж)2
, /М (а,ж) + ^_^а,ж) Жі-(а,ж) хі — (а,ж)
+———ї—-у,, ц9 , ^—–иш[х + —————а————–еі) =
13^2 /|М|2 “ (а?х) 1-а! 1-а!
(л/1 — а2/1М|2 — (а,ж)2 + а(а, ж))(а^/||ж||2 — (а, ж)2 — л/1 — а2(а, ж))
л/Цж||2 – (а,ж):
о+
(1 — а2) л/||ж||2 — (а, ж)2 + ал/1 — а2(а, ж)
Н————–^——-…… . _——————ж.
л/Цж||2 – (а,ж)2 Итак, получаем следующую формулу:
й(х,К(а, а)) =
( 0, если ж Є К (а, а);
||ж||, если ж ^ К (а, а) и ж Є —К (а, л/1 — а2);
а^/||ж||2 — (а, ж)2 — л/1 — а2(а, ж),
если ж £ К (а, а), х $ —К(а, л/1 — а2) •
(2)
3°. Пусть ф — непрерывная на отрезке [а, Ь функция действительного переменного такая, что / ф2(х)сІ,х = 1, а — произвольное число из (0,1). Обозначим через М{ф,а) следующее множество
М(ф, а) = < д Є Сіам : / д{х)ф{х)йх ^ а
і
д2(х)с1х
Рассмотрим следующую экстремальную задачу: для любой функции / € С>ад найти
df = іп£ ■
(/(ж) — д(х))2йх : дЄМ(ф,а)
Результаты пункта 2° позволяют сформулировать следующую теорему.
Теорема 2.4.1. Для любой функции / € С{ад существует единственная непрерывная функция € С[ад, которая доставляет инфимум в задаче (3). При этом
Г о,
если / € М(ф,а);
df = <
если / 0 М(ф, а) и / € -М(ф,у/- а2); а{$1 /2{х^х – f(x)ф(x)dx)2)2 – л/1 – а2 /“ f(x)ф(x)dx,
если / ^ М(ф,а) и / ^ —М(ф, VI – а2).
Функция равна /, если / € М(ф,а); равна 0, если / ^ М(ф,а) и / € ; если же / ^ М(ф, а) и / ^ —М(ф, л/1 — а2), то
– а2 ( [а f2(x)dx – (/о /(х)ф(х^х)2 )’ + а /а /(х)ф(х^х Л/ =———^—-:———————–^—–,————х
1аР(Фх – (/*/{х)ф{х^х)2
( (
2 2
а
V V
f2(x)dx
f(x)ф(x)dx
х/Т^-а2 /{х)ф{х^х
Ф+
(1 — а2) ^/аЬ f2(x)dx — (/о6/(ж)^(ж)б?ж)2^ “+ал/Г^а2 §^$(х)ф(х^х
1а /2(фх – (/аЬ/{х)ф{хЦх)2
Литература
1. Худалов В. Т. Регулярные конусы в гильбертовом пространстве // Сиб. мат. журн.—1996.— Т. 37, № 1.—С. 193-196.
2. Худалов В. Т. Аппроксимативные свойства положительной и отрицательной частей элемента в упорядоченных банаховых пространствах // Мат. заметки.—1996.—Вып. 5.—С. 793-798.
3. Худалов В. Т. В гильбертовом пространстве регулярность конуса равносильна самосопряженности // Матем. заметки.
4. Худалов В. Т. Упорядоченные банаховы пространства и их приложения.—Владикавказ, 1999.— 200 с.
5. Хорн Р., Джонстон Ч. Матричный анализ.—М.: Мир, 1989.—655 с.