Всё про окружность и круг
Окружность – это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.
Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
Квадрат касательной равен произведению секущей на ее внешнюю часть
Центральный угол – это угол, вершина которого совпадает с центром окружности.
Дугой называется часть окружности, заключенная между двумя точками.
Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.
Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.
Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.
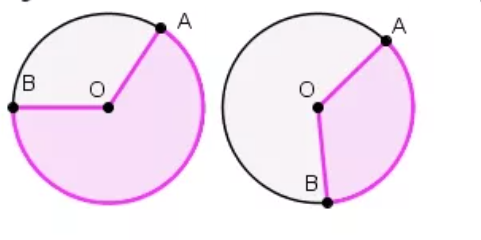
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.
Периметр сектора: P = s + 2R.
Площадь сектора: S = Rs/2 = ПR 2 а/360°.
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.
Расстояние точки до окружности формула
Всё про окружность и круг
Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.
Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
Квадрат касательной равен произведению секущей на ее внешнюю часть
Центральный угол — это угол, вершина которого совпадает с центром окружности.
Дугой называется часть окружности, заключенная между двумя точками.
Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.
Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.
Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.
Периметр сектора: P = s + 2R.
Площадь сектора: S = Rs/2 = ПR 2 а/360°.
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.
Окружность и круг
теория по математике 📈 планиметрия
Определения
Окружность – множество всех точек плоскости, равноудаленных от одной данной точки (центра окружности). Другими словами – это замкнутая линия, длину которой можно измерить.
На рисунке центр окружности обозначен точкой О. 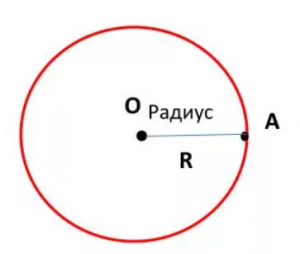
Радиус – расстояние от центра до любой точки окружности. На рисунке радиус обозначен АО. Все радиусы одной окружности равны. Радиус можно обозначать латинскими буквами R или r.
Диаметр – отрезок, который соединяет две точки окружности и проходит через её центр. На рисунке диаметр обозначен АВ. Все диаметры одной окружности равны. В одном диаметре содержится два радиуса. Диаметр обозначается буквой d.
Хорда – отрезок, соединяющий две любые точки окружности. На рисунке это отрезок CD.
Свойство хорд
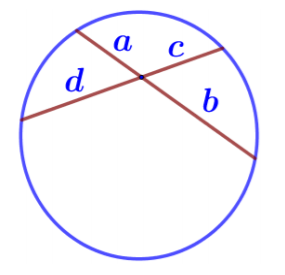
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. Так, на рисунке показаны две пересекающиеся хорды, одна состоит из отрезков a и b, вторая из отрезков d и с, следовательно, ab=dс.
Длина окружности
Длину окружности можно вычислить по формуле:
C=2πR, где π=3,14.
Дуга – часть окружности, которая соединяет две точки. На рисунке мы видим несколько дуг, например, дуги CD (малая и большая). Дуга АВ – называется полуокружностью, так как стягивает концы диаметра. Обозначается дуга значком ∪АВ.
Дуга, касательная, круг, сектор, сегмент
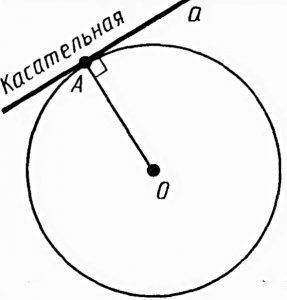
Из точки, не лежащей на окружности можно провести касательную – прямую, которая имеет с окружностью только одну общую точку (рисунок 4).
Свойства касательной
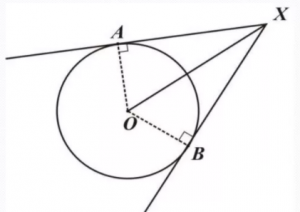
На рисунке видно, что АХ=ВХ, угол АХО равен углу ВХО.
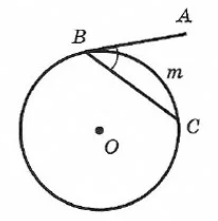
Угол АВС (образован касательной АВ и хордой ВС) равен половине дуги m.
Круг – часть плоскости, ограниченная окружностью. Другими словами, круг – это всё, что находится внутри окружности.
Площадь круга вычисляется по формуле:
S=πR 2 , где π=3,14.
Сектор и его площадь
Сектор – область круга, ограниченная двумя радиусами. На рисунке сектор выделен сиреневым цветом, он ограничен радиусами ОА и ОВ.
Площадь кругового сектора вычисляется по формуле:
S= π R 2 360 . . × α , где α – угол между радиусами.
Сегмент – это область круга, ограниченная хордой и дугой. На рисунке сегмент выделен сиреневым цветом. Также можно сказать, что это часть круга, отсекаемая от него хордой. На рисунке видно, как хорда АВ отсекает сегмент.
Длина окружности
О чем эта статья:
6 класс, 9 класс, ЕГЭ/ОГЭ
Если вы не знаете, как обозначается длина окружности, то знак окружности выглядит вот так — l
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Как найти длину окружности через диаметр
Хорда — это отрезок, который соединяет две точки окружности.
Диаметр — хорда, которая проходит через центр окружности. Формула длины окружности через диаметр:
π— число пи — математическая константа, примерно равная 3,14
d — диаметр окружности
Как найти длину окружности через радиус
Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:
π — число пи, примерно равное 3,14
r — радиус окружности
Это две основные формулы для вычисления длины окружности. Ниже мы покажем еще несколько формул, которые вы сможете доказать самостоятельно, пользуясь основными формулами и свойствами геометрических фигур.
Как вычислить длину окружности через площадь круга
Если вам известна площадь круга, вы также можете узнать длину окружности:
π — число пи, примерно равное 3,14
S — площадь круга
Как найти длину окружности через диагональ вписанного прямоугольника
Как измерить окружность, если в нее вписан прямоугольник:
π — число пи, примерно равное 3,14
d — диагональ прямоугольника
Как вычислить длину окружности через сторону описанного квадрата
Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:
π — математическая константа, примерно равная 3,14
a — сторона квадрата
Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:
π — математическая константа, она примерно равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника
Как найти длину окружности через площадь и полупериметр описанного треугольника
Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.
π — математическая константа, примерно равная 3,14
S — площадь треугольника
p — полупериметр треугольника
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:
π — математическая константа, примерно равная 3,14
a — сторона многоугольника
N — количество сторон многоугольника
Задачи для решения
Давайте тренироваться! Двигаемся от простого к сложному:
Задача 1. Найти длину окружности, диаметр которой равен 5 см.
Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:
Подставляем туда известные переменные и получается, что длина окружности равна
Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм
Решение. Радиус окружности равен Подставим туда наши переменные и получим
Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.
Обучение на курсах по математике поможет закрепить полученные знания на практике.
Наименьшее расстояние между точкой и окружностью
Данный круг с данным радиусом имеет свой центр в определенной позиции в координатной плоскости. В координатной плоскости задается другая точка. Задача — найти кратчайшее расстояние между точкой и окружностью.
Примеры:
Подход :
который равен (др)
d = √ ((x2-x1) ^ 2 — (y2-y1) ^ 2)
Ниже приведена реализация вышеуказанного подхода:
// C ++ программа для поиска
// Наименьшее расстояние
// между точкой и
// круг
#include
using namespace std;
// Функция для поиска кратчайшего расстояния
void dist( double x1, double y1, double x2, double y2, double r)
cout “The shortest distance “
“between a point and a circle is “
sqrt (( pow ((x2 – x1), 2))
double x1 = 4, y1 = 6,
x2 = 35, y2 = 42, r = 5;
dist(x1, y1, x2, y2, r);
// Java-программа для поиска
// Наименьшее расстояние
// между точкой и
// круг
// Функция для поиска кратчайшего расстояния
static void dist( double x1, double y1, double x2,
double y2, double r)
System.out.println( “The shortest distance “
+ “between a point and a circle is “
+ (Math.sqrt((Math.pow((x2 – x1), 2 ))
+ (Math.pow((y2 – y1), 2 )))
public static void main(String[] args)
double x1 = 4 , y1 = 6 ,
x2 = 35 , y2 = 42 , r = 5 ;
dist(x1, y1, x2, y2, r);
/ * Этот код предоставлен PrinciRaj1992 * /
# Python программа для поиска
# Наименьшее расстояние
# между точкой и
# круг
# Функция поиска кратчайшего расстояния
def dist(x1, y1, x2, y2, r):
print ( “The shortest distance between a point and a circle is “
,((((x2 – x1) * * 2 ) + ((y2 – y1) * * 2 )) * * ( 1 / 2 )) – r);
dist(x1, y1, x2, y2, r);
# Этот код предоставлен 29AjayKumar
// C # программа для поиска кратчайшего расстояния
// между точкой и окружностью
// Функция для поиска кратчайшего расстояния
static void dist( double x1, double y1, double x2,
double y2, double r)
Console.WriteLine( “The shortest distance “
+ “between a point and a circle is “
+ (Math.Sqrt((Math.Pow((x2 – x1), 2))
+ (Math.Pow((y2 – y1), 2)))
public static void Main(String[] args)
double x1 = 4, y1 = 6,
x2 = 35, y2 = 42, r = 5;
dist(x1, y1, x2, y2, r);
/ * Этот код предоставлен PrinciRaj1992 * /
// PHP программа для поиска
// Наименьшее расстояние
// между точкой и
// круг
// Функция для поиска кратчайшего расстояния
function dist( $x1 , $y1 , $x2 , $y2 , $r )
echo “The shortest distance between a point and a circle is “
[spoiler title=”источники:”]
http://b4.cooksy.ru/articles/rasstoyanie-tochki-do-okruzhnosti-formula
[/spoiler]
Ученик
(161),
на голосовании
10 лет назад
Голосование за лучший ответ
FILIN
Искусственный Интеллект
(114614)
10 лет назад
Сначала напишите уравнение прямой, проходящей через М и центр окружности точку
О (-1;2). Далее, найдите точки пересечения этой прямой с окружностью. Подсчитайте расстояния до этих точек от точки М. Выберете из них наименьшее. Это будет ответом.
I’m looking for a way to find out the distance from a point outside a circle to a point on a circle, where the point on the circle is based on radians, degrees, or both (whatever the formula works with).
With this, I know the distance from the point to the circle ($x$), and the radius of the circle ($r$). I also know how many degrees ($theta$) from a starting point on the circle, which is on the line between the point outside the circle and the center of the circle.
So, I’m dealing with simple right triangles here, but what I don’t know how to get is the lengths of opposite and adjacent arms given a number of degrees.
Here is an poorly drawn GIF to help understand what I want. The red line is what I’m trying to get.
Thanks for all your help.
Наименьшее расстояние между точкой и окружностью
29.12.2019Геометрия, Математика
Данный круг с данным радиусом имеет свой центр в определенной позиции в координатной плоскости. В координатной плоскости задается другая точка. Задача — найти кратчайшее расстояние между точкой и окружностью.
Примеры:
Input: x1 = 4, y1 = 6, x2 = 35, y2 = 42, r = 5 Output: 42.5079 Input: x1 = 0, y1 = 0, x2 = 5, y2 = 12, r = 3 Output: 10
Подход :
который равен (др)
d = √ ((x2-x1) ^ 2 — (y2-y1) ^ 2)

Ниже приведена реализация вышеуказанного подхода:
C ++
#include <bits/stdc++.h>
using namespace std;
void dist(double x1, double y1, double x2, double y2, double r)
{
cout << "The shortest distance "
<< "between a point and a circle is "
<< sqrt((pow((x2 - x1), 2))
+ (pow((y2 - y1), 2)))
- r
<< endl;
}
int main()
{
double x1 = 4, y1 = 6,
x2 = 35, y2 = 42, r = 5;
dist(x1, y1, x2, y2, r);
return 0;
}
Джава
class GFG
{
static void dist(double x1, double y1, double x2,
double y2, double r)
{
System.out.println("The shortest distance "
+ "between a point and a circle is "
+ (Math.sqrt((Math.pow((x2 - x1), 2))
+ (Math.pow((y2 - y1), 2)))
- r));
}
public static void main(String[] args)
{
double x1 = 4, y1 = 6,
x2 = 35, y2 = 42, r = 5;
dist(x1, y1, x2, y2, r);
}
}
python3
def dist(x1, y1, x2, y2, r):
print("The shortest distance between a point and a circle is "
,((((x2 - x1)** 2) + ((y2 - y1)** 2))**(1/2)) - r);
x1 = 4;
y1 = 6;
x2 = 35;
y2 = 42;
r = 5;
dist(x1, y1, x2, y2, r);
C #
using System;
class GFG
{
static void dist(double x1, double y1, double x2,
double y2, double r)
{
Console.WriteLine("The shortest distance "
+ "between a point and a circle is "
+ (Math.Sqrt((Math.Pow((x2 - x1), 2))
+ (Math.Pow((y2 - y1), 2)))
- r));
}
public static void Main(String[] args)
{
double x1 = 4, y1 = 6,
x2 = 35, y2 = 42, r = 5;
dist(x1, y1, x2, y2, r);
}
}
PHP
<?php
function dist($x1, $y1, $x2, $y2, $r)
{
echo "The shortest distance between a point and a circle is "
,sqrt((pow(($x2 - $x1), 2))
+ (pow(($y2 - $y1), 2)))
- $r ;
}
$x1 = 4;
$y1 = 6;
$x2 = 35;
$y2 = 42;
$r = 5;
dist($x1, $y1, $x2, $y2, $r);
?>
Выход:
The shortest distance between a point and a circle is 42.5079
Рекомендуемые посты:
- Наименьшее расстояние от центра круга до хорды
- Наименьшее расстояние между линией и точкой в трехмерной плоскости
- Найти кратчайшее расстояние между любой парой двух разных хороших узлов
- Проверьте, можно ли соединить две точки на круге так, чтобы расстояние между ними составляло k
- Соседи точки по кругу по алгоритму Брезенхэма
- Проверьте, существует ли точка в круговом секторе или нет.
- Найти, если точка лежит внутри круга
- Расстояние между точкой и плоскостью в 3 D
- Перпендикулярное расстояние между точкой и линией в 2 D
- Найдите радиусы окружностей, которые выстроены в ряд, и дайте расстояние между центрами первого и последнего круга.
- Найти минимальный радиус такой, чтобы как минимум точка k лежала внутри круга
- Оптимальное расположение точки для минимизации общего расстояния
- Найти минимальную сумму расстояния до A и B от любой целой точки в кольце размера N
- Соотношение расстояния между центрами окружностей и точкой пересечения двух прямых общих касательных к окружностям
- Соотношение расстояния между центрами окружностей и точкой пересечения двух поперечных общих касательных к окружностям
Наименьшее расстояние между точкой и окружностью
0.00 (0%) 0 votes
Александр Мельник
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение окружности
Определение 1
Окружность — геометрическая фигура, состоящая из всех точек, расположенных на равном расстоянии от заданной точки.
Определение 2
В рамках определения 1, заданная точка называется центром окружности.
Определение 3
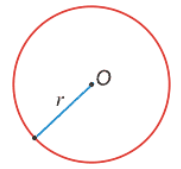
Отрезок, соединяющий центр окружности с любой ее точкой называется радиусом окружности $(r)$ (Рис. 1).
Рисунок 1. Окружность с центром в точке $O$ и радиусом $r$
Определение 4
Отрезок, соединяющий две любые точки окружности, называется хордой.
Определение 5
Хорда, проходящая через центр окружности, называется диаметром $(d)$.
[d=2r]
Взаимное расположение прямой и окружности
Окружность имеет три возможных взаимных расположений относительно прямой:
-
Если расстояние от центра окружности до прямой меньше радиуса, то прямая имеет две точки пересечения с окружностью.
-
Если расстояние от центра окружности до прямой равно радиусу, то прямая имеет две точки пересечения с окружностью.
-
Если расстояние от центра окружности до прямой больше радиуса, то прямая имеет две точки пересечения с окружностью.
Уравнение окружности
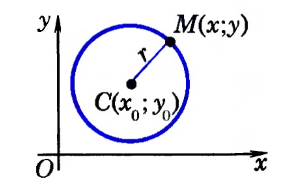
Выведем уравнение окружности в декартовой системе координат $xOy$. Пусть центр окружности $C$ имеет координаты $(x_0,y_0)$, а радиус окружности равен $r$. Пусть точка $M$ с координатами $(x,y)$ — произвольная точка этой окружности (рис. 2).
Рисунок 2. Окружность в декартовой системе координат
«Окружность» 👇
Расстояние от центра окружности до точки $M$ вычисляется следующим образом
Но, так как $M$ лежит на окружности, то по определению 3, получаем $CM=r$. Тогда получим следующее
Уравнение (1) и есть уравнение окружности с центром в точке $(x_0,y_0)$ и радиусом $r$.
В частности, если центр окружности совпадает с началом координат. То уравнение окружности имеет вид
Длина окружности
Выведем формулу длины окружности $C$ через её радиус. Для этого рассмотрим две окружности с длинами $C$ и $C’$ и радиусами $R$ и $R’$. Впишем в ним правильные $n-угольники$ с периметрами $P$ и $P’$ и длинами сторон $a$ и $a’$ соответственно. Как нам известно, сторона вписанного -угольника равна
Тогда, получим
Следовательно
Неограниченно увеличивая количество сторон правильных многоугольников $n$ получим, что
Отсюда, получаем
То есть
Получили, что отношение длины окружности к её диаметру постоянное число для любой окружности. Эту константу принято обозначать числом $pi approx 3,14$. Таким образом, получим
Формула (2) и есть формула для вычисления длины окружности.
Пример задачи на понятие окружность
Пример 1
Найти уравнение окружности с центром в точке $(1, 2)$. Проходящей через начало координат и найти длину данной окружности.
Решение.
Найдем сначала уравнение данной окружности. Для этого будем использовать формулу (1). Так как центр окружности лежит в точке $(1, 2)$, получим
[{(x-1)}^2+{(y-2)}^2=r^2]
Найдем радиус окружности как расстояние от точки $(1, 2)$ до точки $(0,0)$
[r=sqrt{{(1-0)}^2+{(2-0)}^2}=sqrt{5}]
Получаем, уравнение окружности имеет вид:
[{(x-1)}^2+{(y-2)}^2=5]
Найдем длину окружности по формуле (2). Получим
[C=2pi r=10pi ]
Ответ: ${(x-1)}^2+{(y-2)}^2=5$, $C=10pi $
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме