Макеты страниц
Расстояния играют фундаментальную роль при обработке информации, заключенной в образе. Данный параграф посвящен обсуждению расстояний, используемых при предварительной обработке и выделении признаков. Рассмотрение начинается с расстояний, разделяющих отдельные точки, а затем путем обобщения соответствующих понятий вводятся расстояния между точкой и множеством и расстояния между множествами.
(а) Расстояние между точками
В  -мерном евклидовом пространстве расстояние между двумя точками а и b определяется как
-мерном евклидовом пространстве расстояние между двумя точками а и b определяется как

где а и b суть n-мерные векторы, k-e компоненты которых равны  соответственно.
соответственно.
(б) Расстояние между точкой и множеством
Расстояние между точкой, соответствующей образу  и множеством точек, соответствующих образам
и множеством точек, соответствующих образам  представляющих класс К образов, определяется как среднеквадратичное расстояние между х и К элементами множества
представляющих класс К образов, определяется как среднеквадратичное расстояние между х и К элементами множества  . Квадрат
. Квадрат
расстояния между точками х и  равен
равен

В таком случае среднеквадратичное расстояние определяется как

(в) Внутримножественное расстояние
Расстояние внутри множества точек, соответствующих образам  определяется как
определяется как

Из (7.2.2) имеем

Частное среднее для фиксированной точки а и точек а, соответствующих всем  оставшимся точкам множества
оставшимся точкам множества  определяется по формуле (7.2.3) подстановкой вместо
определяется по формуле (7.2.3) подстановкой вместо  точки
точки  . Следовательно,
. Следовательно,

Отметим, что при  соответствующее слагаемое равно нулю и его можно безболезненно исключить. Выражение содержит К членов, однако только
соответствующее слагаемое равно нулю и его можно безболезненно исключить. Выражение содержит К членов, однако только  из них отличны от нуля.
из них отличны от нуля.
Аналогично определяем среднее по всем К точкам множества  что позволяет представить внутримножественное расстояние как
что позволяет представить внутримножественное расстояние как

Внутримножественное расстояние можно выразить также через дисперсии значений компонент точек, представляющих образы.

(кликните для просмотра скана)
Следовательно, используя несмещенную оценку выборочной дисперсии, получаем выражение для внутримножественного расстояния

Это расстояние будет использоваться в следующих разделах при изучении преобразования кластеризации и упорядочения признаков.
(г) Расстояние между множествами
Расстояние между множествами  состоящих из
состоящих из  выборочных образов соответственно, определяется как
выборочных образов соответственно, определяется как

Это выражение, однако, не так уж легко свести к простому замкнутому виду, используя статистические характеристики. Другой способ измерения расстояний между множествами связан с использованием расстояния между центроидами двух рассматриваемых множеств или расстояния Махаланобнса, о котором шла речь в гл. 4.
Напомним,
что
в точечном евклидовом пространстве En
расстояние
между точками
P(x1,
x2,…
xn),
Q(y1,
y2,…
yn)
вычисляется по формуле
(P,
Q)
= ,
если
координаты точек заданы относительно
ортонормированной системы координат.
Мы можем рассматривать это расстояние,
как функцию, сопоставляющую двум точкам
P
и Q
число (P,
Q).
Функция
обладает следующими свойствами:
1.
(P,
Q)
=
(Q,
P);
2.
(P,
Q)
+
(Q,
R)
(P,
R)
(неравенство треугольника);
3.
(P,
Q)
0, и (P,
Q)
=
0
P
=
Q.
Пусть
теперь M
– произвольное множество, элементы
которого будем называть точками. Пусть
на M
задана функция ,
сопоставляющая любым двум точкам P,
QM
число (P,
Q),
которое называется расстоянием между
этими точками, и такая что выполнены
свойства (аксиомы) 1,
2,
3.
Тогда пара (M,
)
называется метрическим
пространством,
а функция
– метрикой.
Примеры
1. Пусть V
– произвольное подмножество евклидова
пространства. Расстояние между двумя
точками P,
QV
будем считать
таким же, как во всем пространстве. Тогда
(V,
)
– метрическое пространство. Метрика
называется
индуцированной
из En.
2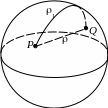
.
Сфера S2
в трехмерном геометрическом пространстве.
Расстояние 1
между P,
Q
S2
определяется
как длина кратчайшей кривой по поверхности,
соединяющей P
и Q.
Как известно, этой кривой
является дуга большой окружности
(у которой радиус равен радиусу сферы).
Мы
также можем определить расстояние
как в примере 1: (P,
Q)
– это длина
хорды PQ.
Тогда (S2,
1)
и (S2,
)
– это разные метрические пространства.
3.
Определим
на плоскости расстояние между точками
A(x1,
y1),
B(x2,
y2)
по формуле 2(A,
B)=|x2
x1|+|y2
y1|.
Получается, что 2(A,
B)
равно длине ломаной AMB,
изображённой на следующем чертеже.
У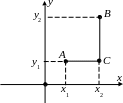
пражнение.
Самостоятельно
про-верьте, что для плоскости с метрикой
2
выполняются
все аксиомы метрического пространства.
Диаметром
множества
V
в метрическом пространстве (M,
)
называется
точная верхняя грань расстояний между
точками этого множества:
d(V)
= sup;sdo10(P
(P,
Q).
Расстоянием
между двумя множествами
V,
W
называется
точная нижняя грань расстояний между
точками этих множеств:
(V,
W)
= inf;sdo10(P(V
(P,
Q).
В
частности, если одно из множеств состоит
из одной точки, то получаем определение
расстояния
от точки до множества.
П
очему
в этом определении супрэмум, а не
максимум, инфинум, а не минимум? Поясним
на примере.
Пример.
Пусть V
– это открытый (без границы) круг радиуса
1 на плоскости с центром в начале
координат, а W
= Q(2,0).
Тогда d(V)
= 2,
хотя таких точек, расстояние между
которыми равно 2 в V
нет. Таким образом, максимум не
достигается. Аналогично, (Q,
V)
= 1,
хотя такой точки PV,
что (Q,
P)
= 1
не существует. Значит, минимум не
достигается.
Отметим,
что если множества пересекаются, то
расстояние между ними равно нулю.
Обратное неверно. Например, если W
есть прямая x
=
1, то (V,
W)
= 0,
но V
W=.
Определение.
Множество V
в метрическом пространстве (M,
)
называется
ограниченным,
если d(V)<.
Заметим,
что и всё метрическое пространство
может быть ограниченным, как например,
(S2,
1).
Упражнение.
Чему равны
диаметры метрических пространств (S2,
1)
и (S2,
)?
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Методы Оптимизации. Даниил Меркулов. Отделимость. Проекция. Опорная гиперплоскость
Interior
Внутренность множества
Внутренностью множества $S$ называется следующее множество:
$$mathbf{int} (S) = {mathbf{x} in S mid exists varepsilon > 0, B(mathbf{x}, varepsilon) subset S}$$
где $B(mathbf{x}, varepsilon) = mathbf{x} + varepsilon B$ – шар с центром в т.$mathbf{x}$ и радиусом $varepsilon$
Относительная внутренность множества
Относительной внутренностью множества $S$ называется следующее множество:
$$mathbf{relint} (S) = {mathbf{x} in S mid exists varepsilon > 0, B(mathbf{x}, varepsilon) cap mathbf{aff} (S) subseteq S}$$

- Любое непустое выпуклое множество $S subseteq mathbb{R}^n$ имеет непустую относительную внутренность $mathbf{relint}(S)$
Projection
Расстояние между точкой и множеством
Расстоянием $d$ от точки $mathbf{y} in mathbb{R}^n$ до замкнутого множества $S subset mathbb{R}^n$ является:
$$d(mathbf{y}, S, | cdot |) = inf{|x – y| mid x in S }$$
Проекция точки на множество
Проекцией точки $mathbf{y} in mathbb{R}^n$ на множество $S subseteq mathbb{R}^n$ называется точка $pi_S(mathbf{y}) in S$: $$| pi_S(mathbf{y}) – mathbf{y}| le |mathbf{x} – mathbf{y}|, forall mathbf{x} in S$$
- Если множество – открыто, и точка в нем не лежит, то её проекции на это множество не существует
- Если точка лежит в множестве, то её проекция – это сама точка
- $$pi_S(mathbf{y}) = underset{mathbf{y}}{operatorname{argmin}} |mathbf{x}-mathbf{y}|$$
- Пусть $S subseteq mathbb{R}^n$ – выпуклое замкнутое множество. Пусть так же имеются точки $mathbf{y} in mathbb{R}^n$ и $mathbf{pi} in S$. Тогда если для всех $mathbf{x} in S$ справедливо неравенство: $$langle pi -mathbf{y}, mathbf{x} – pirangle ge 0, $$ то $pi$ является проекцией точки $mathbf{y}$ на $S$, т.е. $pi_S (mathbf{y}) = pi$
- Пусть $S subseteq mathbb{R}^n$ – афинное множество. Пусть так же имеются точки $mathbf{y} in mathbb{R}^n$ и $mathbf{pi} in S$. Тогда $pi$ является проекцией точки $mathbf{y}$ на $S$, т.е. $pi_S (mathbf{y}) = pi$ тогда и только тогда, когда для всех $mathbf{x} in S$ справедливо равенство: $$langle pi -mathbf{y}, mathbf{x} – pirangle = 0 $$
Пример 1
Найти $pi_S (y) = pi$, если $S = {x in mathbb{R}^n mid |x – x_c| le R }$, $y notin S$
Решение:

-
Из рисунка строим гипотезу: $pi = x_0 + R cdot frac{y – x_0}{|y – x_0|}$
-
Проверяем неравенство для выпуклого замкнутого множества: $(pi – y)^T(x – pi) ge 0$
$$left( x_0 – y + R frac{y – x_0}{|y – x_0|} right)^Tleft( x – x_0 – R frac{y – x_0}{|y – x_0|} right) =$$
$$left( frac{(y – x_0)(R – |y – x_0|)}{|y – x_0|} right)^Tleft( frac{(x-x_0)|y-x_0|-R(y – x_0)}{|y – x_0|} right) =$$
$$frac{R – |y – x_0|}{|y – x_0|^2} left(y – x_0 right)^Tleft( left(x-x_0right)|y-x_0|-Rleft(y – x_0right) right) = $$
$$frac{R – |y – x_0|}{|y – x_0|} left( left(y – x_0 right)^Tleft( x-x_0right)-R|y – x_0| right) =$$
$$left(R – |y – x_0| right) left( frac{(y – x_0 )^T( x-x_0)}{|y – x_0|}-R right)$$
Первый сомножитель отрицателен по выбору точки $y$. Второй сомножитель так же отрицателен, если применить к его записи теорему Коши – Буняковского: $$(y – x_0 )^T( x-x_0) le |y – x_0||x-x_0|$$
$$frac{(y – x_0 )^T( x-x_0)}{|y – x_0|} – R le frac{|y – x_0||x-x_0|}{|y – x_0|} – R = |x – x_0| – R le 0$$
Пример 2
Найти $pi_S (y) = pi$, если $S = {x in mathbb{R}^n mid c^T x = b }$, $y notin S$
Решение:

-
Из рисунка строим гипотезу: $pi = y + alpha c$. Коэффициент $alpha$ подбирается так, чтобы $pi in S$: $c^T pi = b$, т.е.: $$c^T (y + alpha c) = b$$
$$c^Ty + alpha c^T c = b$$
$$c^Ty = b – alpha c^T c$$ -
Проверяем неравенство для выпуклого замкнутого множества: $(pi – y)^T(x – pi) ge 0$
$$(y + alpha c – y)^T(x – y – alpha c) = $$
$$ alpha c^T(x – y – alpha c) = $$
$$ alpha (c^Tx) – alpha (c^T y) – alpha^2 c^Tc) = $$
$$ alpha b – alpha (b – alpha c^T c) – alpha^2 c^Tc = $$
$$ alpha b – alpha b + alpha^2 c^T c – alpha^2 c^Tc = 0 ge 0$$
Пример 3
Найти $pi_S (y) = pi$, если $S = {x in mathbb{R}^n mid Ax = b, A in mathbb{R}^{m times n}, b in mathbb{R}^{m} }$, $y notin S$
Решение:

-
Из рисунка строим гипотезу: $pi = y + sumlimits_{i=1}^malpha_i A_i = y + A^T alpha$. Коэффициент $alpha$ подбирается так, чтобы $pi in S$: $A pi = b$, т.е.: $$c^T (y + A^T alpha) = b$$
$$A(y + A^Talpha) = b$$
$$Ay = b – A A^Talpha$$ -
Проверяем неравенство для выпуклого замкнутого множества: $(pi – y)^T(x – pi) ge 0$
$$(y + A^Talpha – y)^T(x – y – A^Talpha) = $$
$$ alpha^T A(x – y – A^Talpha) = $$
$$ alpha^T (Ax) – alpha^T (A y) – alpha^T AA^T alpha) = $$
$$ alpha^T b – alpha^T (b – A A^Talpha) – alpha^T AA^T alpha = $$
$$ alpha^T b – alpha^T b + alpha^T AA^T alpha – alpha^T AA^T alpha = 0 ge 0$$
Separation
Отделимые множества
Множества $S_1$ и $S_2$ называются отделимыми, если существуют $mathbf{p} neq mathbf{0} in mathbb{R}^n$ и $beta in mathbb{R}$, что:
$$langle mathbf{p}, mathbf{x_1}rangle le beta le langle mathbf{p}, mathbf{x_2}rangle, ;; forall mathbf{x_1} in S_1, ;; forall mathbf{x_2} in S_2$$

Собственно отделимые множества
Множества $S_1$ и $S_2$ называются собственно отделимыми, если они отделимы и дополнительно можно указать такие $mathbf{x_1} in S_1, mathbf{x_2} in S_2$
$$langle mathbf{p}, mathbf{x_1}rangle < langle mathbf{p}, mathbf{x_2}rangle$$

Строго отделимые множества
Множества $S_1$ и $S_2$ называются строго отделимыми, если существует $mathbf{p} neq mathbf{0} in mathbb{R}^n$, что:
$$langle mathbf{p}, mathbf{x_1}rangle < langle mathbf{p}, mathbf{x_2}rangle, ;; forall mathbf{x_1} in S_1, ;; forall mathbf{x_2} in S_2$$

Сильно отделимые множества
Множества $S_1$ и $S_2$ называются сильно отделимыми, если существуют $mathbf{p} neq mathbf{0} in mathbb{R}^n$ и $beta in mathbb{R}$, что:
$$ underset{mathbf{x_1} in S_1}{operatorname{sup}} langle mathbf{p}, mathbf{x_1}rangle < beta < underset{mathbf{x_2} in S_2}{operatorname{inf}}langle mathbf{p}, mathbf{x_2}rangle, ;; forall mathbf{x_1} in S_1, ;; forall mathbf{x_2} in S_2$$


Расстояние между множествами
Расстоянием между множествами $S_1$ и $S_2$ называется число:
$$d(S_1, S_2,| cdot |) = underset{mathbf{x_1} in S_1, mathbf{x_2} in S_2}{operatorname{inf}} |mathbf{x_1} – mathbf{x_2}|$$
- Если $X$ и $Y$ – непустые выпуклые множества в $mathbb{R}^n$ и $X cap Y = emptyset$, тогда $X$ и $Y$ – отделимы.
- Если $X$ – непустое выпуклое замкнутое множество в $mathbb{R}^n$ и $mathbf{y} notin X$, тогда точку $mathbf{y}$ можно строго отделить от множества $X$.
Supporting hyperplane
Опорная гиперплоскость
Гиперплоскость $Gamma_{p,beta} = left{mathbf{x} in mathbb{R}^n : langle p, mathbf{x} rangle > beta right}$ называется опорной к множеству $S$ в граничной точке $mathbf{a} in partial S$, если $$langle p, mathbf{x} rangle ge beta = langle p, mathbf{a} rangle ;; forall mathbf{x} in S$$
Опорная гиперплоскость называется собственно опорной, если, кроме того, можно указать $mathbf{x_0} in S: langle p, mathbf{x_0} rangle > beta$
- В любой граничной (относительно граничной) точке выпуклого множества существует опорная (собственно опорная) гиперплоскость.
- Касательная плоскость к поверхности $F(x) = 0,$ где $F: mathbb{R}^n rightarrow mathbb{R}^1$ в точке $x_0$ определяется уравнением: $$nabla F(x_0)^T(x-x_0) = 0$$
- Касательная плоскость к графику функции $f(x),$ где $f: mathbb{R}^n rightarrow mathbb{R}^1$ в точке $x_0$ определяется уравнением: $$phi(x) = f(x_0) + nabla f(x_0)^T(x-x_0) = 0$$
Пример 4
Построить гиперплоскость, разделяющую $S_1$ и $S_2$:
$$S_1 = left{ x in mathbb{R}^2 mid x_1 x_2 ge 1, x_1 > 0right}, ;;; S_2 = left{ x in mathbb{R}^2 mid x_2 le frac{4}{x_1 – 1} +9right}$$
Решение:
- Найдем $partial S_1 cap partial S_2$:
$$
begin{cases}
x_1 x_2 = 1
x_2 = frac{4}{x_1 – 1} +9
end{cases}
$$
$$
begin{cases}
x_1 = frac{1}{3}
x_2 = 3
end{cases}
$$
т.е. множества пересекаются в точке $x_0 = (frac{1}{3}, 3)$
- Построим касательные плоскости к обеим поверхностям в точке пересечения:
$$
begin{cases}
nabla F_1(x_0)^T(x-x_0) = 0
nabla F_2(x_0)^T(x-x_0) = 0
end{cases}
$$
$$
begin{cases}
3 x_1 + frac{1}{3}x_2 – 2 = 0 \
-6 x_1 – frac{2}{3}x_2 + 4 = 0
end{cases}
$$
Итого, получаем: $9x_1 + x_2 = 6$, т.е. $p = (9,1), beta = 6$
Пример 5
Построить опорную гиперплоскость для множества $S = left{ x in mathbb{R}^2 mid e^{x_1} le x_2right}$ в граничной точке $x_0 = (0,1)$
Решение:
- Имеем поверхность $F(x_1, x_2) = e^{x_1} – x_2, ;;; nabla F = (e^{x_1}, -1), ;;; nabla F(x_0) = (1,-1)$
- Тогда $$nabla F(x_0)^T(x-x_0) = 0$$
$$(1,-1)^T (x_1, x_2 – 1) = 0$$ - Искомая опорная гиперплоскость: $x_1 – x_2 + 1 = 0$
Пример 6
Построить опорную гиперплоскость для множества $S = left{ x in mathbb{R}^3 mid x_3 ge x_1^2 + x_2^2right}$ так, чтобы она отделяла его от точки $x_0 = left(-frac{5}{4}, frac{5}{16}, frac{15}{16}right)$
Решение:
-
Заметим, что здесь $x_0 notin partial S$. А значит, таких гиперплоскостей много. Возможный вариант: искать опорную гиперплоскость в точке $pi_S(x_0) = pi in S$. Значит, $Gamma_{p, beta} = left{ x in mathbb{R}^3 mid p^Tx = beta, p^T pi = beta right}$
-
Будем искать $pi$, решая задачу минимизации:
$$underset{x in partial S}{operatorname{min}}|x – x_0|^2$$
$$underset{x in partial S}{operatorname{min}}(x – x_0)^T(x – x_0)$$
Учитывая структуру множества $partial S = {x in mathbb{R}^3 mid x_3 = x_1^2 + x_2^2}$, можем перейти к задаче безусловной минимизации.
$$ left( x_1 + frac{5}{4} right)^2 + left( x_2 – frac{5}{16} right)^2 + left( x_1^2 + x_2^2 – frac{15}{16} right)^2 rightarrow operatorname{min}$$
Единственным решением которой является точка $pi = left( -1, frac{1}{4}, frac{17}{16}right)$.
- Тогда $p = x_0 – pi = left( -frac{1}{4}, frac{1}{16}, -frac{1}{8}right), ;; beta = p^T pi = frac{17}{128}$
Домашнее задание 3
-
Найти $pi_S (y) = pi$, если $S = {x in mathbb{R}^n mid c^T x ge b }$
-
Найти $pi_S (y) = pi$, если $S = {x in mathbb{R}^n mid x = x_0 + X alpha, X in mathbb{R}^{n times m}, alpha in mathbb{R}^{m}}$, $y notin S$
-
Построить гиперплоскость, разделяющую $S_1$ и $S_2$:
$$S_1 = left{ x in mathbb{R}^n mid x_1^2 + x_2^2 + ldots + x_n^2 le 1right}, ;;; S_2 = left{ x in mathbb{R}^n mid x_1^2 + x_2^2 + ldots + x_{n-1}^2 + 1 le x_n right}$$ -
Построить опорную гиперплоскость для множества $S = left{ x in mathbb{R}^3 mid frac{x_1^2}{4}+frac{x_2^2}{8}+frac{x_3^2}{25} le 1 right}$ в граничной точке $x_0 = left(-1, frac{12}{5}, frac{sqrt{3}}{2}right)$
-
Пусть $S subset mathbb{R}^n$ – замкнутое выпуклое множество, $mathbf{x} in S$. Найти множество $Y subset mathbb{R}^n$ такое, что $forall mathbf{y} in Y$ выполнено $mathbf{x} = pi_S(mathbf{y})$
-
Пусть даны $mathbf{x} in mathbb{R}^n$ и выпуклый конус $K subseteq mathbb{R}^n$. Пусть $Y = mathbf{x} + K$, $mathbf{y} in Y$. Найти множество $X subset mathbb{R}^n,$ такое, что $mathbf{x} in X, forall mathbf{y} in Y: x = pi_X(mathbf{y})$
В качестве решения необходимо предоставить либо:
-
.pdfфайл, сверстанный с помощью $ LaTeX $ с решениями задач -
.ipynbс оформленным решением
Asked
7 years, 5 months ago
Viewed
2k times
$begingroup$
Let $M={x: x_{1}^{2}+x_{2}^{2}+x_{3}^{2}le4, x_{1}^{2}-4x_{2}le0}$ and $y=(1,0,2)^{T}$. Find the minimum distance from $y$ to $M$, the unique minimizing point and a separating plane. Does anyone know how to solve the problem without KKT conditions? It would be very helpful.
asked Dec 16, 2015 at 21:15
LauraLaura
3331 silver badge5 bronze badges
$endgroup$
5
1 Answer
$begingroup$
Finding the minimum distance from $y$ to $M$ can be done by solving the following problem: Minimize
$$
d=(x_1-1)^2+{x_2}^2+(x_3-2)^2quadquad quad mbox{(the squared distance to $y$)}
$$
subject to:
begin{align}
{x_1}^2+{x_2}^2+{x_3}^2&le 4\
{x_1}^2-4{x_2}&le 0
end{align}
You can solve this with KKT conditions if you are familiar with non linear optimization. Actually this also gives you the unique minimizing point (its coordinates are the triplet $(x_1,x_2,x_3)$ of the solution).
Youem
7,06011 silver badges33 bronze badges
answered Dec 16, 2015 at 21:56
![]()
KuifjeKuifje
9,4492 gold badges13 silver badges35 bronze badges
$endgroup$
5
You must log in to answer this question.
Not the answer you’re looking for? Browse other questions tagged
.
Not the answer you’re looking for? Browse other questions tagged
.
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
Atatushka |
Заголовок сообщения: Найти расстояние от точки до множества в ЛНП
|
||
|
В линейном нормированном пространстве [math]C[0;1][/math] найти расстояние от точки [math]x_0(t)=0[/math] до множества [math]M=left{x(t)colon ,x(0)=0,~int_0^1 x(t),dt=1right}[/math];
|
||
| Вернуться к началу |
|
||
|
Atatushka |
Заголовок сообщения: Re: Найти расстояние от точки до множества в ЛНП
|
|
Мне не очень понятно это решение
|
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Найти расстояние от элемента до множества
в форуме Функциональный анализ, Топология и Дифференциальная геометрия |
ag15 |
5 |
813 |
23 дек 2014, 13:38 |
|
Для данного множества найти кодовое расстояние
в форуме Дискретная математика, Теория множеств и Логика |
any5957 |
0 |
539 |
26 июн 2015, 10:20 |
|
Найти расстояние от точки до плоскости
в форуме Геометрия |
Ekubovich |
16 |
756 |
29 дек 2021, 12:47 |
|
Найти расстояние от точки P(7,9,7) от прямой
в форуме Аналитическая геометрия и Векторная алгебра |
mkolmi |
1 |
798 |
27 ноя 2017, 19:26 |
|
Найти: Расстояние от точки С до прямой АВ
в форуме Аналитическая геометрия и Векторная алгебра |
rightgame |
3 |
530 |
14 янв 2017, 16:42 |
|
Найти расстояние от точки до параболы
в форуме Исследование операций и Задачи оптимизации |
whit3_1 |
9 |
362 |
13 ноя 2021, 15:11 |
|
Найти координаты точки, зная расстояние
в форуме Аналитическая геометрия и Векторная алгебра |
Veinar |
5 |
2654 |
11 янв 2014, 21:25 |
|
Найти расстояние от точки до основания башни
в форуме Тригонометрия |
afraumar |
11 |
902 |
23 авг 2014, 10:37 |
|
Найти расстояние от точки на окружности до прямой
в форуме Геометрия |
Secret |
16 |
5856 |
31 май 2013, 19:38 |
|
Найти все крайние точки множества
в форуме Исследование операций и Задачи оптимизации |
Class |
1 |
429 |
09 мар 2018, 20:37 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 5 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group
Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru
Русская поддержка phpBB





