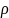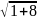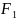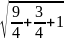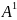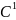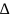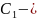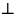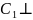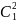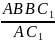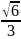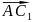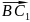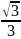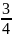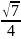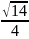Как найти расстояние от точки до вершины

Вершина любой плоской или объемной геометрической фигуры однозначно определяется своими координатами в пространстве. Точно так же может быть однозначно определена и любая произвольная точка в той же системе координат, а это дает возможность вычислить расстояние между этой произвольной точкой и вершиной фигуры.

Вам понадобится

– бумага;
– ручка или карандаш;
– калькулятор.

Инструкция

Сведите задачу к нахождению длины отрезка между двумя точками, если координаты заданной в условиях задачи точки и вершины геометрической фигуры известны. Эту длину можно вычислить, воспользовавшись теоремой Пифагора применительно к проекциям отрезка на оси координат – она будет равна квадратному корню из суммы квадратов длин всех проекций. Например, пусть в трехмерной системе координат заданы точка A(X₁;Y₁;Z₁) и вершина C объемной фигуры любой геометрической формы с координатами (X₂;Y₂;Z₂). Тогда длины проекций отрезка между ними на координатные оси можно определить как X₁-X₂, Y₁-Y₂ и Z₁-Z₂, а длину самого отрезка – как √((X₁-X₂)²+(Y₁-Y₂)²+(Z₁-Z₂)²). Например, если координаты точки A(5;9;1), а вершины C(7;8;10), то расстояние между ними будет равно √((5-7)²+(9-8)²+(1-10)²) = √(-2²+1²+(-9)²) = √(4+1+81) = √86 ≈ 9,274.

Вычислите сначала координаты вершины, если в явном виде в условиях задачи они не представлены. Конкретный способ расчета зависит от типа фигуры и известных дополнительных параметров. Например, если известны трехмерные координаты трех вершин параллелограмма A(X₁;Y₁;Z₁), B(X₂;Y₂;Z₂) и C(X₃;Y₃;Z₃), то координаты четвертой его вершины (противоположной вершине B) будут равны (X₃+X₂-X₁; Y₃+Y₂-Y₁; Z₃+Z₂-Z₁). После определения координат недостающей вершины вычисление расстояния между ней и произвольной точкой вновь сведется к определению длины отрезка между двумя этими точками в заданной системе координат – сделайте это тем же способом, который был описан в предыдущем шаге. Например, для вершины описанного в этом шаге параллелограмма и точки E с координатами (X₄;Y₄;Z₄) формулу вычисления расстояния из предыдущего шага можно изменить так: √((X₃+X₂-X₁-X₄)²+(Y₃+Y₂-Y₁-Y₄)²+(Z₃+Z₂-Z₁-Z₄)²).

Для практических расчетов можно использовать, например, встроенный в поисковую систему Google калькулятор. Так, чтобы вычислить значение по формуле, полученной на предыдущем шаге, для точек с координатами A(7;5;2), B(4;11;3), C(15;2;0), E(7;9;2), введите такой поисковый запрос: sqrt((15+4-7-7)^2+(2+11-5-9)^2+(0+3-2-2)^2). Поисковик рассчитает и отобразит результат вычислений (5,19615242).

Видео по теме

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Марианна Бурыкина

Извини. что не по теме. Не знаю куда ещё написать. Наткнулась на твой старый вопрос по поступлению в вуз РХБЗ. И никто там ничего не ответил. Чтобы здесь с ссылками не парится прошу найти самой инфу : военная академия РХБЗ и инженерных войск им. Маршала Советского Союз С. к. Тимошенко. Находится в Костроме, девушки там учатся, можешь даже в контакте найти те кто учился в ней. Меня туда не приняли из-за травмы старой, ещё в военкомате в известном направлении послали, но ничего не сказали касаемо пола – это обрадовало=) Удачи, если не передумала=)) Завидую белой завистью если у тебя нету останавливающих проблем со здоровьем)))

Источник

Your best bet is to iterate over all the lines and find the minimum distance from a point to a line segment.

To find the distance from a point to a line segment, you first find the distance from a point to a line by picking arbitrary points P1 and P2 on the line (it might be wise to use your endpoints). Then take the vector from P1 to your point P0 and find (P2-P1) . (P0 - P1) where . is the dot product. Divide this value by ||P2-P1||^2 and get a value r.

Now if you picked P1 and P2 as your points, you can simply check if r is between 0 and 1. If r is greater than 1, then P2 is the closest point, so your distance is ||P0-P2||. If r is less than 0, then P1 is the closest point, so your distance is ||P0-P1||.

If 0<r<1, then your distance is sqrt(||P0-P1||^2 - (r * ||P2-P1||)^2)

The pseudocode is as follows:

for p1, p2 in vertices:

  var r = dotProduct(vector(p2 - p1), vector(x - p1))
  //x is the point you're looking for

  r /= (magnitude(vector(p2 - p1)) ** 2)

  if r < 0:
    var dist = magnitude(vector(x - p1))
  else if r > 1:
    dist = magnitude(vector(p2 - x))
  else:
    dist = sqrt(magnitude(vector(x - p1)) ^ 2 - (r * magnitude(vector(p2-p1))) ^ 2)

  minDist = min(dist,minDist)

Источник

Как найти расстояние между двумя точками?

Расстоянием между точками также называют прямую,
у которой одна из точек это начало, а соответственно
другая конец. Найти расстояние между этими
двумя точками, значит найти длину прямой,
связывающей точки.

Есть много разных способов найти расстояние между
двумя точками, но самый универсальный, на мой взгляд,
это найти расстояние взяв за основу Теорему Пифагора.
Исходя из этой теоремы, можно сказать, что в нашем
случае расстоянием(прямой), является гипотенуза,
а чем тогда являются точки, сейчас разберемся.

Формулировка великой Теоремы Пифагора звучит так:
в прямоугольном треугольнике квадрат гипотенузы равен
сумме квадратов катетов. Или же кратко, формулой:
( c^2 = a^2 + b^2 ) где c — это гипотенуза, a и b — катеты.

Формулировка этой теоремы применяется почти всегда и везде,
где нужно найти расстояние от чего-то до чего-то. Сейчас, мы
используя эту теорему найдем расстояние между точками.

Итак, для примера возьмем точки с координатами
первой точки — x1 = 0; y1 = 4, второй точки — x2 =3; y2 = 0.
Как же нам теперь выразить точки через катеты a и b ?
Читайте дальше, все гениальное просто.

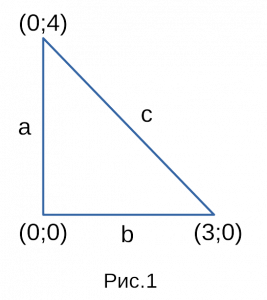
На рисунке 1 мы изобразили для наглядности
прямоугольный треугольник, с координатами
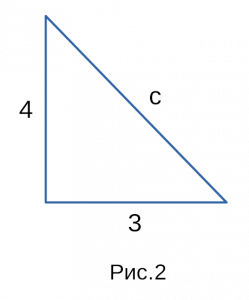
которые мы взяли для примера. На рисунке 2
тот же самый прямоугольный треугольник,
только без координат! Эти два прямоугольных
треугольника идентичные, поэтому вернемся
к Теореме Пифагора.

Заменяем длины катетов a и b, из Теоремы Пифагора,
на разность координат точек. Взгляните на формулу,
которая получилась:

Подставляем наши координаты:

В итоге получилось, что расстояние в нашем примере
равно 5(корень из 25). Как видите все просто, и вы можете
смело применять эту формулу, решая не только задачи,
но и на практике, находя расстояние зная только две точки.

Все формулы для треугольника

1. Как найти неизвестную сторону треугольника

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c – стороны произвольного треугольника

α , β , γ – противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), ( a):

2. Как узнать сторону прямоугольного треугольника

Есть следующие формулы для определения катета или гипотенузы

a , b – катеты

c – гипотенуза

α , β – острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

Формулы сторон по теореме Пифагора, ( a , b ):

3. Формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

b – сторона (основание)

a – равные стороны

α – углы при основании

β – угол образованный равными сторонами

Формулы длины стороны (основания), (b ):

Формулы длины равных сторон , (a):

4. Найти длину высоты треугольника

Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.

H – высота треугольника

a – сторона, основание

b, c – стороны

β , γ – углы при основании

p – полупериметр, p=(a+b+c)/2

R – радиус описанной окружности

S – площадь треугольника

Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):

Расстояние от точки до прямой

Что называется расстоянием от точки до прямой? Как найти расстояние от точки до прямой?

Расстоянием от точки до прямой называется длина перпендикуляра, опущенного из данной точки на прямую.

Таким образом, чтобы найти расстояние от точки до прямой, надо из точки к прямой провести перпендикуляр и найти его длину.

Например, на рисунке 1 расстояние от точки A до прямой a равно длине перпендикуляра AB, опущенного из точки A на прямую a.

Задачи на нахождение расстояния от точки до прямой сводятся к рассмотрению прямоугольного треугольника.

№ 1. Из точки к прямой проведены две наклонные, длины которых относятся как 2:3, а длины их проекций соответственно равны 2 см и 7 см. Найти расстояние от точки до прямой.

Дано: A∉a,

BC и BD — их проекции, BC=2 см, BD=7 см

1) Пусть k — коэффициент пропорциональности. Тогда AC=2k см, AD=3k см.

2) Рассмотрим треугольник ABC — прямоугольный (так как AB — перпендикуляр к прямой a по условию). По теореме Пифагора

3) Аналогично, из треугольника ABD

4) Приравниваем правые части полученных равенств и находим k:

5) Зная k, найдем AB:

№ 2. Из точки к прямой проведены две наклонные, длины которых равны 13 см и 15 см. Найти расстояние от точки до прямой, если разность проекций наклонных равна 4 см.

Дано: A∉a,

AC и AD — наклонные, AC=13 см, AD=15 см,

BC и BD — их проекции, BD-BC=4 см

1) Пусть BC=x см, тогда BD=x+4 см.

3) Аналогично, из треугольника ABD

4) Приравниваем правые части полученных равенств и находим x:

5) Зная x, найдем AB:

№ 3. Найти расстояние от точки A до прямой a, если известно, что наклонная AF, длина которой равна c, образует с прямой a угол α.

Дано: A∉a,

Треугольник ABF — прямоугольный (так как AB — перпендикуляр к прямой a по условию). AB — катет, противолежащий углу ACB, AF — гипотенуза.

[spoiler title=”источники:”]

http://www-formula.ru/2011-10-09-11-08-41

Расстояние от точки до прямой

[/spoiler]

Источник

Координатный
метод является естественным продолжением
векторного метода, то есть вектор
пространства есть упорядоченная тройка
действительных чисел (декартовых
прямоугольных координат вектора в
ортонормированном базисе). Рациональное
расположение фигуры относительно
системы координат (некоторые вершины
многогранника находятся на координатных
осях), позволяет при решении задач
упростить вычисления.

Основные
формулы, применяемые при решении задач
координатным методом:

(М,
)
=
,
где М (
).
Плоскость

задана уравнением ах+bу+сz+d=0.

cos

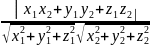
координаты
вершин некоторых многогранников, часто
используемых при решении задач, приведены
в приложении №2

Практическая часть.

3.1. Расстояние между двумя точками.

Основные
теоремы, применяемые при нахождении
расстояния между двумя точками – теорема
Пифагора, теорема косинусов.

Основные
формулы, применяемые при решении задач
координатным методом:

Р
асстояние
между двумя т очками можно вычислить
по формуле:
Ρ(А,В)
=
,
где А(
;
;
),
B(
;
;
).

│=
,
где {a, b, c} координаты вектора

.

ример
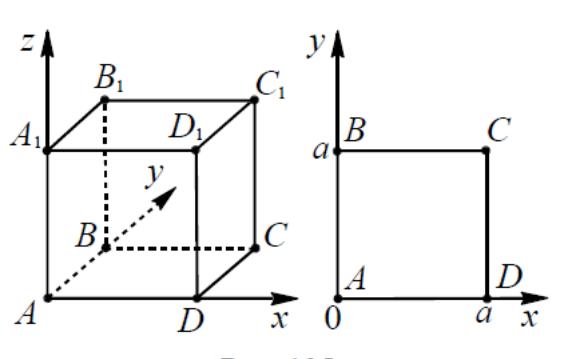
1.Ребра
правильной четырехугольной призмы
равны 1, 4 и 4. Найдите расстояние от
вершины до центра основания призмы, не
содержащего эту вершину.

Решение.
Поэтапно вычислительный метод. АС
=4

, АО=2

,

О=
=3
Координатный метод.

(0,0,1),
О (2,2,0)

О
=

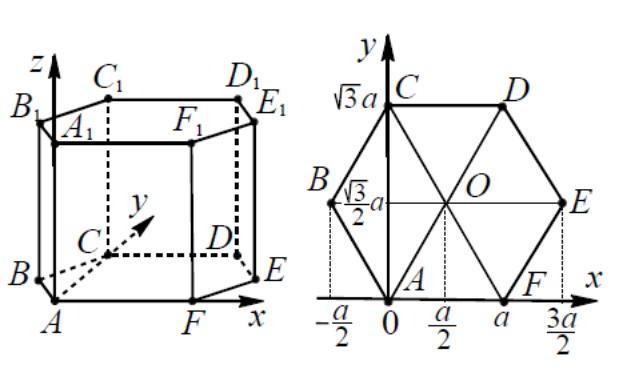
Пример
2.
.В правильной шестиугольной призме
ABCDEF

,
все ребра которой равны 1, найдите
расстояние между точками A
и

.
Решение.
Поэтапно вычислительный метод. АЕ
=

,
(По теореме косинусов из ∆ AEF),
А
=
2. Ответ. 2

Координатный
метод. А(0,0,0),

(
;

;1),
А
=

=
2. Ответ. 2

3.2. Расстояние от точки до прямой

Расстояние
от точки до прямой,
не содержащей эту точку, есть длина
отрезка перпендикуляра, проведенного
из этой точки на прямую.
Расстояние
между двумя параллельными прямыми
равно длине
отрезка их общего перпендикуляра.
Расстояние
между двумя параллельными прямыми
равно
расстоянию от любой точки одной из этих
прямых до другой прямой.

поэтапно-вычислительный
метод

1.Расстояние
от точки до прямой можно вычислить, как
длину отрезка перпендикуляра, если
удается включить этот отрезок в некоторый
треугольник в качестве одной из высот.
2. Еще один подход к нахождению расстояния
от точки А до прямой а состоит в том,
чтобы найти основание

перпендикуляра, опущенного из точки А
на прямую а. Если точка

находится
вне участка прямой а, данного в задаче,
то через точку А проводят прямую с,
параллельную а, и выбирают на ней более
удобную точку С, ортогональная проекция
которой

принадлежит данному участку прямой а.

Пример
1.
1. В кубе A…D1, все ребра которого равны
1, найдите расстояние от точки B до прямой
AC1.

Р
ешение.
1 способ. Поэтапно-вычислительный.
1. Построим вспомогательный

АВ

прямоугольный (АВ

ВС, следовательно, по теореме о трех
перпендикулярах В

АВ). По
свойству диагонали куба имеем: А

= 3А

, А

. АВ=1, В
=

. 2. В прямоугольном треугольнике АВ

найдем высоту, проведенную из
вершины прямого угла, длина которой
является расстоянием от точки В до
прямой AC1. ВН=

, ВН=

2
способ. Координатный.
Введем прямоугольную систему координат:
ось абсцисс пойдет по прямой АД, ось
ординат по ДС, ось аппликат по прямой
Д
.
Тогда В(1;1;0), C1(0;1;1),
А(1;0;0).

{-1;1;1},