Как найти расстояние от вершины до ребра - Сайт, где вы сможете решить свои вопросы

Автор

Сообщение

Заголовок сообщения: Пирамида. Расстояние от вершины до ребра

Добавлено: 25 ноя 2013, 22:14

Начинающий

Зарегистрирован:
25 ноя 2013, 22:00
Сообщений: 3
Cпасибо сказано: 0
Спасибо получено:
0 раз в 0 сообщении
Очков репутации: 1

Здравствуйте! Требуется помощь.

Даны координаты вершин тетраэдра А1 А2 А3 А4 .
А1 ( 1, -1, 2 ); А2 ( 2, 1, 2 ); А3 ( 1, 1, 4 ); А4 ( 6, -3, 8 )

Найти: расстояние вершины А4 до ребра А1 А2

Вернуться к началу

gur88	Заголовок сообщения: Re: Пирамида. Расстояние от вершины до ребра Добавлено: 26 ноя 2013, 03:40
	Уравнение нашел, но вот формулу, по которой нужно искать расстояние, найти не могу, в этом-то и проблема.
Вернуться к началу

mad_math	Заголовок сообщения: Re: Пирамида. Расстояние от вершины до ребра Добавлено: 26 ноя 2013, 11:16
	Yurik писал(а): И на лекциях её вряд-ли дают. Нам давали. Но я и не настаиваю, просто показала альтернативный вариант, а выбор варианта решения остаётся за ТС.
Вернуться к началу

gur88	Заголовок сообщения: Re: Пирамида. Расстояние от вершины до ребра Добавлено: 26 ноя 2013, 17:04
	Всё, всем спасибо! Всё сделал.
Вернуться к началу

Источник

Скачать материал

Сейчас обучается 390 человек из 62 регионов

Сейчас обучается 269 человек из 65 регионов

Описание презентации по отдельным слайдам:

1 слайд

Правильная пирамида
Выполнила Петренко Наталья Викторовна,
Учитель математики МОУ СОШ №7,
Ст.Воронежской, Усть – Лабинского района,
Краснодарского края
3 слайд

В правильной четырехугольной пирамиде известны длина стороны основания 2 и длина высоты 2. Найдите:
а) объем пирамиды;
б) площадь боковой поверхности;
в) угол наклона бокового ребра к плоскости основания;
г) угол наклона боковой грани к плоскости основания;
д) радиус вписанного шара;
е) радиус описанного шара;
ж) расстояние от вершины пирамиды до плоскости основания;
4 слайд

з) расстояние от вершины пирамиды до ребра основания;
и) расстояние от ребра основания до противоположной грани;
к) расстояние между боковым ребром и скрещивающейся с ним диагональю основания;
л) объем вписанного конуса;
м) площадь боковой поверхности описанного конуса.
Выход
5 слайд

а) КО – высота пирамиды

В
О
К
2
б) Проведем апофему КТ и найдем
ее длину из Δ КОТ:
В
2
6 слайд

А
С
D
2
В
В) Так как в правильной пирамиде все
углы наклона всех боковых ребер к
плоскости основания равны, то найдем
например, <КСО. Рассмотрим ΔКСО
КО=2, ОС=0,5 АС, где АС – диагональ
квадрата АВСD, значит
К
О
?
7 слайд

А
С
D
2
В
г) Так как в правильной пирамиде
углы наклона всех боковых граней
к плоскости основания равны, то
найдем, например, угол наклона
боковой грани KCD к плоскости АВС.
так как KT DC, то OT DC, поэтому
< КТО -линейный угол искомого
двугранного угла. Рассмотрим Δ КТО:
КО=2.
Т
К
О
?
8 слайд

А
С
D
2
В
д) Так как двугранные углы при основании
правильной пирамиды равны, то центр
вписанного шара (точка О1) принадлежит
высоте КО. Обозначим радиус вписанного
шара буквой r. Рассмотрим Δ КТО:
О1Р=О1О= r. Используя подобие треугольников Δ КТО и Δ КО1Р, имеем:
К
Т
О
О
Т
К
О1
Р
9 слайд

А
С
D
2
В
е) Так как боковые ребра правильной
пирамиды равны, то центр описанного
шара (точка О2) лежит на прямой КО.
Обозначим радиус описанного шара
через R. Рассмотрим Δ КСО.
По теореме Пифагора из Δ О2ОС:
Получаем, что центр описанного шара
совпадает с точкой О.
К
О
О2
О
К
С
ж) Расстояние от точки К до
плоскости АВС равно
длине отрезка КО и равно 2.
10 слайд

А
С
D
2
В
з) Так как в правильной пирамиде
расстояния от вершины до ребер
основания равны, то найдем,
например, расстояние от точки
К до ребра СD, Это расстояние
равно длине апофемы КТ и равно
K
O
T
и) Так как прямая DС параллельна
плоскости АВК (по признаку
параллельности прямой и плоскости),
то расстояние от прямой DС до
плоскости АВК равно расстоянию
от любой точки прямой DС до этой
плоскости. Рассмотрим на прямой
ВС точку Т. И из Δ ЕКТ (точка Е —
середина АВ) найдем искомое
расстояние. Это расстояние равно
длине высоты ТН. Найдем длину ТН,
выразив двумя способами площадь
Δ ЕКТ.
Е
Е
К
Т
О
Н
РЕШЕНИЕ
11 слайд

А
С
D
2
В
К
К) Найдем расстояние от ребра КС до диагонали
ВD.Проведем высоту OF в Δ КСО и докажем , что
OF- общий перпендикуляр к прямым КС и ВD.
1) OF┴ КС по построению
2) Так как ВD ┴(КСО) (По признаку
перпендикулярности прямой и
Плоскости), а OF (КСО), то ВD┴OF
3)Найдем длину OF, используя
площадь Δ КСО
О
F
12 слайд

А
С
D
2
В
1) Введем прямоугольную систему координат.
Пусть SN- общий перпендикуляр прямых KC
и BD. Найдем длину вектора SN
2)Так как SD коллинеарен BD, то
существует такое число х, что
Найдем координаты векторов:
Векторно-координатный метод
z
x
y
K
O
S
N
14 слайд

А
С
D
2
В
л) Высота вписанного конуса равна высоте
пирамиды, а радиус основания конуса
равен радиусу окружности, вписанной в
квадрат АВСD, поэтому
м) Образующая описанного конуса равна
боковому ребру пирамиды, а радиус
основания конуса равен радиусу
окружности, описанной около квадрата
АВСD, поэтому
K
O
15 слайд

Спасибо за внимание.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 261 454 материала в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

16.12.2020
189
0

02.12.2020
360
32

01.12.2020
178
0

25.11.2020
109
0

01.11.2020
130
0

19.08.2020
284
1

10.08.2020
139
0

27.07.2020
101
0

Вам будут интересны эти курсы:

Курс профессиональной переподготовки «Маркетинг: теория и методика обучения в образовательной организации»
Курс повышения квалификации «Методика написания учебной и научно-исследовательской работы в школе (доклад, реферат, эссе, статья) в процессе реализации метапредметных задач ФГОС ОО»
Курс повышения квалификации «Организация научно-исследовательской работы студентов в соответствии с требованиями ФГОС»
Курс повышения квалификации «Экономика и право: налоги и налогообложение»
Курс профессиональной переподготовки «Клиническая психология: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Правовое регулирование рекламной и PR-деятельности»
Курс профессиональной переподготовки «Организация менеджмента в туризме»
Курс повышения квалификации «Страхование и актуарные расчеты»
Курс повышения квалификации «Основы менеджмента в туризме»
Курс профессиональной переподготовки «Управление ресурсами информационных технологий»
Курс повышения квалификации «Психодинамический подход в консультировании»
Курс повышения квалификации «Мировая экономика и международные экономические отношения»
Курс профессиональной переподготовки «Управление качеством»

Источник

2.1. Определение точки пересечения прямой с гранями пирамиды

Заданная
прямая
m(m₁,m₂₎
является прямой общего положения. Для
нахождения точек пересечения прямой
с гранями пирамиды необходимо через
эту прямую провести вспомогательную
проецирующую плоскость, например,
фронтально-проецирующую. Найти проекции
линии сечения вспомогательной плоскости
с гранями пирамиды. Точки пересечения
проекции заданной прямой с проекцией
линии сечения и есть точки пересечения
прямой с пирамидой.

Рассмотрим
нахождение точек пересечения прямой
m
с гранями пирамиды ABCS
(рис. 3).

Порядок построений.

1.
Проводим через прямую общего положения
m
фронтально-проецирующую плоскость P.
Эта плоскость задается своим фронтальным
следом: P₂≡m₂.
Фронтальная проекция линии сечения
(1₂3₂2₂)
пирамиды ABCS
этой плоскостью совпадает с проекцией
прямой m₂
и фронтальным следом этой плоскости
Р₂.
Рассмотрим фронтальные проекции точек
1₂,
2₂,
3₂
пересечения ребер пирамиды со
вспомогательной плоскостью
Р₂,
найдем их горизонтальные проекции.
Проекция точки 1₁
находится как принадлежащая отрезку
CS,
а точки 2₁,
как принадлежащая отрезку AS.
Точка 3
лежит на профильной прямой уровня BS.
Найти проекцию 3₁
только с помощью линии связи невозможно.
Для нахождения проекции 3₁
через проекцию 3₂
проводим прямую уровня (горизонталь),
лежащую в плоскости грани ABS
и параллельную
ребру AB:
3₂4₂|| В₂А₂,
4₁3₁|| А₁В₁.
Таким образом, находим проекцию 3₁.
Соединив проекции точек 1₁,
2₁,
3₁,
находим горизонтальную проекцию линии
сечения. Выделяем ее и ее фронтальную
проекцию зеленым цветом.

2.
Проекции точек L₁
и N₁,
лежащие на линии сечения, являются
горизонтальными проекциями точек
пересечения прямой m
с пирамидой. С помощью линий связи
находим

Рис.3
Нахождение точек пересечения прямой
m
с гранями пирамиды ABCS

фронтальные
проекции точек пересечения
L₂,
N₂
прямой m
с пирамидой_.

2.2. Определение натуральной величины сечения пирамиды проецирующей плоскостью

Рассмотрим
сечение пирамиды ABCS
фронтально-проецирующей плоскостью
Р₂,
которое найдено при решении предыдущей
задачи. Фигура сечения, определенная
точками 1,
2, 3, представляет
из себя треугольник, являющийся
фронтально-проецирующей плоскостью
(рис. 4).

Плоская
фигура проецируется на плоскость
проекций в натуральную величину в том
случае, когда она параллельна этой
плоскости проекций, т.е. является
плоскостью уровня.

Порядок построений.

Для
того, чтобы фронтально-проецирующую
плоскость, определенную токами 1,
2, 3,
преобразовать в плоскость уровня с
помощью метода замены плоскостей
проекций, введем новую плоскость
проекций П₄с осью
системы плоскостей П₂/П₄|| m₂.
Найденные проекции точек 1₄,
2₄,
3₄
соединим и получим натуральную величину
сечения, которую обведем красным
карандашом.

Определение расстояния от вершины основания до бокового ребра

Расстоянием
от вершины B
до ребра CS
является перпендикуляр, опущенный из
точки B
на прямую
CS.

Для
решения задачи необходимо прямую CS
методом
замены плоскостей проекций
на первом
этапе сделать прямой уровня, а на втором
этапе решения задачи сделать проецирующей
прямой. Тогда перпендикуляр из точки
B
к проецирующей прямой CS
будет прямой уровня и будет проецироваться
на новую плоскость проекций
П₅
в натуральную величину (рис.5).

Рис.4.
Определение натуральной величины
сечения

Рис.5.
Расстояние от вершины основания В до
бокового ребра CS

Порядок
построений.

Используя
метод замены плоскостей проекций,
выбираем новую плоскость П₄
таким образом, чтобы ось системы
плоскостей П₁/П₄
была параллельна проекции ребра C₁S₁.
Ребро CS
является прямой уровня в системе
плоскостей П₁/П₄.
Находим проекцию ребра C₄S₄
и проекцию точки B₄.
Из точки B₄
опускаем перпендикуляр B₄K₄
на отрезок C₄S₄.
Отрезок B₄K₄
является проекцией перпендикуляра,
опущенного из точки B
на отрезок CS,
но не является натуральной величиной
этого перпендикуляра.
При
второй замене плоскостей проекций
располагаем ось системы плоскостей
П₄/П₅
перпендикулярно проекции ребра C₄S₄.
Находим проекцию точки B₅
и точек C₅≡S₅≡K₅.
Проекция отрезка CS
в плоскости П₅
вырождается в точку, так как эта прямая
является проецирующей для плоскости
П₅.
Проекция B₅K₅является
натуральной величиной расстояния от
вершины B
до ребра
CS.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Ответ:

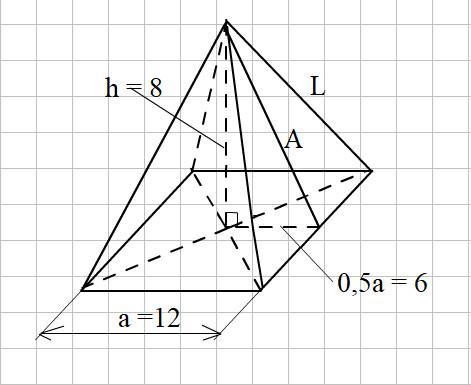
Расстояние от вершины пирамиды до ребра основания равно 10

Объяснение:

Дано:

а = 12 – длина стороны основания пирамиды

h = 8 – высота пирамиды

Найти:

А – расстояние от вершины пирамиды до ребра основания (апофему)

Решение:

$A = sqrt{h^2 + (0.5a)^2} = sqrt{8^2 + 6^2} = 10$

Приложения:

Источник

Ученик

(102),
на голосовании

11 лет назад

Голосование за лучший ответ

Андрей Прудников

Знаток

(491)

11 лет назад

Это будет длина отрезка АС1. чтобы её найти нужно рассмотреть прямоугольный треугольник АСС1. Найти АС по теореме косинусов, получится 12 корней из 3. потом АС1 найти по теореме Пифагора, получится 21

Источник: мозги

AHAPXICT

Профи

(565)

11 лет назад

возьмем треугольник ABC в нем угол В =120 градусов, он равнобедренный
стороны по 12, значит АС/sin B =AB/sin C
AC=AB sin B/Sin C= 12* sin 120/sin30 =12*корень (3)/2 / 1/2 =12 КОРНЕЙ (3)
расстояние от точки А до прямой СД – перпендикуляр в точку C, т. к. угол АСВ=30 градусов, а ВСД = 120. получается прямоугольный треугольник АСС1, где искомая величина есть гипотенузой
АС1=корень (AC^2+CC1^2)=корень (144*3+9)=21 (единица)

Источник

Описание презентации по отдельным слайдам:

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

Другие материалы

Вам будут интересны эти курсы:

2.1. Определение точки пересечения прямой с гранями пирамиды

2.2. Определение натуральной величины сечения пирамиды проецирующей плоскостью

Определение расстояния от вершины основания до бокового ребра

Вам также может понравиться

Как найти массу предмета погруженного в воду

Плинтусовка как исправить самогон

Как найти импульс альфа частицы

Добавить комментарий Отменить ответ