Содержание
- Как найти расстояние от Земли до точки крепления троса?
- Определение расстояния с помощью вертикальной параллаксы
- Измерение расстояния с помощью теодолита
- GPS
- Итог
- Как найти расстояние от земли до точки крепления троса
- Измерение расстояния с помощью троса и линейки
- Метод треугольников
- Использование лазерного дальномера
- Использование альтиметра
- Общий итог
- Как найти расстояние от земли до точки крепления троса
- Использование лазерного дальномера
- Использование теодолита
- Использование нивелира
- Общий итог
Как найти расстояние от Земли до точки крепления троса?
Расстояние от Земли до точки крепления троса может быть измерено несколькими способами. Это очень важно для любой организации, занимающейся работами на высоте, а также для путешественников и любителей альпинизма. В этой статье мы рассмотрим несколько методов вычисления расстояния от Земли до точки крепления троса.
Определение расстояния с помощью вертикальной параллаксы

Один из самых древних способов измерения расстояния до высокой точки заключается в использовании вертикальной параллаксы. Этот метод был изобретен еще в древние времена и до сих пор используется в некоторых случаях.
Вертикальная параллакса обычно рассчитывается путем измерения угла между линией зрения и двумя точками на Земле, расположенными на одной вертикали с высокой точкой. Затем измеряется расстояние между этими двумя точками. Расстояние от Земли до верхней точки находится путем простого математического вычисления с использованием угла и расстояния.
Измерение расстояния с помощью теодолита
Один из современных способов измерения расстояния до высокой точки – использование теодолита. Теодолит – это инструмент, который может измерять вертикальный и горизонтальный углы. Теодолиты используются для строительства зданий, мостов, дорог и других инженерных сооружений.
Для измерения расстояния до высокой точки теодолит устанавливают на земле. Затем он пеленгует высокую точку и измеряет угол между горизонтом и линией зрения. Затем, используя формулы тригонометрии, можно рассчитать расстояние от теодолита до высокой точки.
GPS
GPS – это современная технология, которая используется для определения точного местонахождения объектов на Земле. GPS может также использоваться для определения высоты объекта над уровнем моря.

Используя GPS, можно определить координаты точки крепления троса. Затем при помощи специального программного обеспечения можно рассчитать расстояние от этой точки до уровня моря.
Итог
Таким образом, мы рассмотрели несколько способов измерения расстояния от Земли до точки крепления троса. Каждый из них имеет свои сильные и слабые стороны. Выбор метода зависит от конкретной ситуации, возможностей и требований. Но в любом случае, правильное измерение расстояния до высокой точки – это ключевой фактор безопасности для путешественников, альпинистов и работников, занятых на высоте.
Как найти расстояние от земли до точки крепления троса

Вы находитесь на охоте или на рыбалке в горах, и вам нужно знать расстояние от земли до точки крепления троса. Эта информация будет полезна, чтобы правильно засечь зверя или рыбу, чтобы не оставить лишний шанс на провал. В этой статье мы расскажем вам о том, как можно найти расстояние от земли до точки крепления троса.
Измерение расстояния с помощью троса и линейки
Один из самых простых и доступных способов измерить расстояние от земли до точки крепления троса — это использование троса и линейки. Но для этого нужно, чтобы трос был достаточно длинным. Поднимите трос и закрепите его в точке крепления. Затем стойте на земле, и измерьте расстояние от точки, где вы стоите, до точки на земле, где находится конец троса.
Метод треугольников
Для использования этого метода вам понадобится три точки: точка, откуда вы хотите определить расстояние до точки крепления троса, точка на земле прямо под точкой крепления троса и точка на земле, которая находится в некотором расстоянии от первой точки. Важно, чтобы эти три точки были на одной прямой.
Для большей точности, используйте треугольник с меньшими углами.
Измерьте расстояние между первой и второй точками (точкой на земле, находящейся прямо под точкой крепления троса и точкой, откуда вы хотите измерить расстояние). Затем измерьте расстояние между второй и третьей точками (точка на земле, которая находится в некотором расстоянии от первой точки и точка на земле, находящаяся прямо под точкой крепления троса).
Теперь найдите угол между первой, второй и третьей точками. Вы можете найти этот угол с помощью гониометра. Затем примените теорему синусов, чтобы найти расстояние от земли до точки крепления троса. Формула для вычисления расстояния приведена ниже:
distance = (a * sin(C)) / sin(A), где «a» — расстояние между первой и второй точками, «A» — угол между первой и третьей точками, «C» — угол между второй и третьей точками.
Использование лазерного дальномера

Лазерный дальномер — это устройство, которое использует лазерную технологию для измерения расстояний и обычно используется для геодезических работ. Но вы также можете использовать его, чтобы измерить расстояние от земли до точки крепления троса.
Для использования лазерного дальномера укажите лазерный луч на точку крепления троса, а затем нажмите кнопку на устройстве. Лазерный дальномер измерит расстояние от устройства до точки крепления троса. Некоторые лазерные дальномеры также имеют функцию автоматического вычисления высоты, что упрощает этот процесс.
Использование альтиметра
Альтиметр — это электронное устройство, которое используется для измерения высоты над уровнем моря. Но вы также можете использовать его, чтобы измерить высоту от земли до точки крепления троса. Для этого устройства необходима открытая область, где не будет помех от деревьев или зданий.
Для использования альтиметра поднимите его на высоту до точки крепления троса. Затем найдите текущую высоту над уровнем моря на устройстве. Определите высоту от земли до точки крепления троса, вычтя текущую высоту над уровнем моря из измеренной высоты с помощью альтиметра.
Общий итог
Теперь вы знаете, как можно измерить расстояние от земли до точки крепления троса — с помощью троса и линейки, метода треугольников, лазерного дальномера или альтиметра. Выберите тот метод, который наиболее удобен для вас и вашей конкретной ситуации.
- Измерение с помощью троса и линейки — простой и дешевый способ;
- Метод треугольников — более точный способ, но требующий наличия трех точек на одной прямой;
- Лазерный дальномер — более точный и быстрый способ, но чаще всего имеет высокую цену;
- Альтиметр — менее точный способ, но может быть полезен, если вам нужно измерить высоту над уровнем моря.
Надеемся, что эти советы помогут вам правильно засечь зверя или рыбу.
Как найти расстояние от земли до точки крепления троса
Расстояние от земли до точки крепления троса может быть важным параметром при различных работах, таких как строительство зданий или установка электрических линий. Но как его измерить? На этот вопрос мы ответим в данной статье.
Использование лазерного дальномера
Один из самых простых способов измерить расстояние от земли до точки крепления троса — использование лазерного дальномера. Прибор измеряет расстояние от объекта до себя при помощи лазерного луча. Существуют различные модели лазерных дальномеров, но все они обычно имеют функцию измерения расстояния и точности до нескольких миллиметров.
Важно помнить, что при использовании лазерного дальномера необходимо иметь прямую видимость на точку крепления троса. Если объект находится вне поля зрения дальномера, такой метод измерения не подойдет.
Использование теодолита
Теодолит — это прибор, который используется для измерения горизонтальных и вертикальных углов. Он также может использоваться для измерения расстояния от точки крепления троса до земли. Для того чтобы использовать теодолит, необходимо сначала установить его на точке над землей, на которой будет располагаться прибор. Затем прибор поворачивается в сторону точки крепления, на которой нужно произвести измерение.
Использование теодолита может быть сложным и требовать некоторой подготовительной работы. Для того чтобы измерить расстояние от земли до точки крепления троса при помощи теодолита, необходимо иметь хорошее знание данного прибора и определенный опыт работы с ним.
Использование нивелира

Нивелир — это инструмент, который используется для измерения высоты. Для измерения расстояния от земли до точки крепления троса необходимо установить нивелир на точке, находящейся на земле на некотором расстоянии от точки крепления. Затем направьте нивелир в сторону точки крепления и измерьте угол между земной поверхностью и линией взгляда.
Использование нивелира может привести к неточности результатов если земная поверхность имеет неровности или находится на склоне. Также нивелир может быть неудобен в использовании из-за его веса и габаритов.
Общий итог

Измерение расстояния от земли до точки крепления троса может быть выполнено при помощи лазерного дальномера, теодолита или нивелира. Каждый прибор имеет свои преимущества и недостатки, поэтому выбор инструмента должен зависеть от конкретного случая и целей измерений. Важно помнить, что некоторые методы измерений могут быть сложными и требовать некоторой подготовительной работы, но правильный выбор инструмента может значительно сократить время и обеспечить более точные результаты.
Содержание
- Как измерить расстояние на карте с помощью градусной сетки?
- Расчет расстояний между городами по их координатам
- Введение
- Формулы
- 1. Сферическая теорема косинусов
- 2. Формула гаверсинусов
- 3. Модификация для антиподов
- Определение расстояния между точками по координатам
- Координаты GPS
- Вычисление расстояния между двумя точками через формулу
- Формула для нахождения расстояния между точками
- Способы решения и нахождения расстояния между точками по координатам
- Онлайн-калькулятор для расчета расстояния между точками по координатам
- Картографическая программа для нахождения расстояния между точками
- Откуда берется погрешность при расчете расстояния между точками
Как измерить расстояние на карте с помощью градусной сетки?
С помощью карты можно определять расстояние между точками на земной поверхности, но точность таких вычислений невысока.
Ситуация относительно проста, если точки лежат на одном меридиане. Все меридианы имеют одинаковую длину. Можно подсчитать, что одному градусу широты соответствует примерно 111,3 км реальной длины. Поэтому надо найти разницу в долготе между точками и умножить ее на 111,3 км. Например, если точка А находится на северной широте 50°, а Б располагается на северной широте 32°, и при этом у них совпадает долгота, то расстояние между ними составит.
111,3х(50° – 32°) = 111,3х16 = 1780,8 км
Ситуация меняется, когда одна точка имеет северную, а другая – южную широту. В этом случае широты уже надо складывать. Так, если бы точка Б из предыдущего примера располагалась бы на южной широте 32°, то расстояние от А до Б составило бы:
111,3х(50° + 32°) = 111,3х82 = 9126,6 км
Ситуация усложняется, когда точки находятся на разных меридианах, но на одной параллели. Если у обеих точек долгота западная (или, наоборот, восточная), то сначала надо найти разницу их долгот. Если же одна точка имеет восточную, а другая западную долготу, то их надо суммировать. Далее результат надо умножить на длину 1° параллели. Эта длина у параллелей различна и зависит от их широты. Можно воспользоваться таблицей ниже:
| Широта параллели | Длина ее дуги величиной в 1° |
|---|---|
| 0° | 111,3 |
| 5° | 110,9 |
| 10° | 109,6 |
| 15° | 107,6 |
| 20° | 104,6 |
| 25° | 102,1 |
| 30° | 96,5 |
| 35° | 91,3 |
| 40° | 85,4 |
| 45° | 78,8 |
| 50° | 71,7 |
| 55° | 64,0 |
| 60° | 55,8 |
| 65° | 47,2 |
| 70° | 38,2 |
| 75° | 28,9 |
| 80° | 19,4 |
| 85° | 9,7 |
| 90° | 0 |
Например, нужно найти расстояние между точками, имеющими координаты:
А – 60° с. ш, 39° з. д.
Б – 60° с. ш, 25° з. д.
Широты у них одинаковы, поэтому смотрим на долготу. Она у обеих точек западная, поэтому надо найти их разницу:
39° – 25° = 14°
Полученный результат надо умножить на длину 1° параллели, широта которой составляет 60°. По табличке определяем, что на широте 60° дуга в 1° имеет длину 55,8 км. Перемножаем два числа:
14°х 55,8 км = 781,2 км
Список использованных источников
Источник
Расчет расстояний между городами по их координатам
Расчет расстояний между точками по их координатам на плоскости элементарен, на поверхности Земли — немного посложнее: мы рассмотрим измерение расстояния и начального азимута между точками без проекционных преобразований.
Для начала разберемся в терминологии.
Введение
Длина дуги большого круга – кратчайшее расстояние между любыми двумя точками находящимися на поверхности сферы, измеренное вдоль линии соединяющей эти две точки (такая линия носит название ортодромии) и проходящей по поверхности сферы или другой поверхности вращения.
Сферическая геометрия отличается от обычной Эвклидовой и уравнения расстояния также принимают другую форму. В Эвклидовой геометрии, кратчайшее расстояние между двумя точками – прямая линия. На сфере, прямых линий не бывает. Эти линии на сфере являются частью больших кругов – окружностей, центры которых совпадают с центром сферы.
Начальный азимут — азимут, взяв который при начале движения из точки А, следуя по большому кругу на кратчайшее расстояние до точки B, конечной точкой будет точка B. При движении из точки A в точку B по линии большого круга азимут из текущего положения на конечную точку B постоянно меняется. Начальный азимут отличен от постоянного, следуя которому, азимут из текущей точки на конечную не меняется, но маршрут следования не является кратчайшим расстоянием между двумя точками.

Через любые две точки на поверхности сферы, если они не прямо противоположны друг другу (то есть не являются антиподами), можно провести уникальный большой круг. Две точки, разделяют большой круг на две дуги. Длина короткой дуги – кратчайшее расстояние между двумя точками. Между двумя точками-антиподами можно провести бесконечное количество больших кругов, но расстояние между ними будет одинаково на любом круге и равно половине окружности круга, или π*R, где R – радиус сферы.

На плоскости (в прямоугольной системе координат), большие круги и их фрагменты, как было упомянуто выше, представляют собой дуги во всех проекциях, кроме гномонической, где большие круги — прямые линии. На практике это означает, что самолеты и другой авиатранспорт всегда использует маршрут минимального расстояния между точками для экономии топлива, то есть полет осуществляется по расстоянию большого круга, на плоскости это выглядит как дуга.

Форма Земли может быть описана как сфера, поэтому уравнения для вычисления расстояний на большом круге важны для вычисления кратчайшего расстояния между точками на поверхности Земли и часто используются в навигации.
Вычисление расстояния этим методом более эффективно и во многих случаях более точно, чем вычисление его для спроектированных координат (в прямоугольных системах координат), поскольку, во-первых, для этого не надо переводить географические координаты в прямоугольную систему координат (осуществлять проекционные преобразования) и, во-вторых, многие проекции, если неправильно выбраны, могу привести к значительным искажениям длин в силу особенностей проекционных искажений.
Известно, что более точно описывает форму Земли не сфера, а эллипсоид, однако в данной статье рассматривается вычисление расстояний именно на сфере, для вычислений используется сфера радиусом 6372795 метров, что может привести к ошибке вычисления расстояний порядка 0.5%.
Формулы
Существует три способа расчета сферического расстояния большого круга.
1. Сферическая теорема косинусов
В случае маленьких расстояний и небольшой разрядности вычисления (количество знаков после запятой), использование формулы может приводить к значительным ошибкам связанным с округлением.
φ1, λ1; φ2, λ2 — широта и долгота двух точек в радианах
Δλ — разница координат по долготе
Δδ — угловая разница
Для перевода углового расстояния в метрическое, нужно угловую разницу умножить на радиус Земли (6372795 метров), единицы конечного расстояния будут равны единицам, в которых выражен радиус (в данном случае — метры).
2. Формула гаверсинусов
Используется, чтобы избежать проблем с небольшими расстояниями.

3. Модификация для антиподов
Предыдущая формула также подвержена проблеме точек-антиподов, чтобы ее решить используется следующая ее модификация.
Источник
Определение расстояния между точками по координатам
Спутниковые координаты не только помогают найти маршрут до нужного места, но и позволяют рассчитать отрезок между двумя любыми точками в пространстве или на данной плоскости. Зная необходимые данные и координаты интересующих объектов, можно найти расстояние в километрах или метрах между этими длинами или отрезками нужной длины. Для этого применяется либо сложная формула для самостоятельного решения, либо онлайн-калькуляторы на сайте или картографические программы, выполняющие работу автоматически.
Координаты GPS
Координаты GPS (Global Positioning System) – это цифровые обозначения местоположения устройства в пространстве или на плоскости, указанные в формате соотнесения географических широты и долготы. Данные точки на отрезке определенной длины вычисляются при помощи связи со спутником. Запускается сложная система навигации, которая, помимо указания координат, может определить расстояние между двумя точками в пространстве или на плоскости, проложить маршрут между отрезками длины и рассчитать время перемещения как пешком, так и на разных видах транспорта. В основе работы лежит всемирная система координат WGS 84.
 Координаты GPS
Координаты GPS
Чтобы найти местоположение и расстояние между двумя данными точками или отрезками длины в пространстве и на плоскости по координатам GPS, можно пользоваться как специальным навигатором или профессиональным навигационным прибором, так и обычным смартфоном или планшетом.
Вычисление расстояния между двумя точками через формулу
Найти расстояние между двумя точками в пространстве или на плоскости можно как по прямой, так и по маршруту (с учетом расположения дорог, их поворотов, объездов и пр.). В первом случае применима специальная формула, воспользоваться которой можно как в автоматическом режиме, введя известные данные отрезков в калькулятор на сайте, так и самостоятельно, проведя итоговое решение с нужными материалами на бумаге.
Кратчайшим (прямым) расстоянием считается дуга, проходящая по поверхности Земли от точки А в точку Б. Чтобы найти ее длину, применяют так называемую модифицированную формулу гаверсинусов, учитывающую радиус планеты.
Известно, что Земля – не идеальный шар, а несколько приплюснутый, потому и радиус у нее в разных точках различен. Ввиду этого для подсчета кратчайшего расстояния между точками используется усредненное значение радиуса относительно оси (6372.795 км для Земли), что допускает погрешность итогового значения около 0,5 %.
Формула для нахождения расстояния между точками
В формуле, при помощи которой можно найти расстояния между двумя данными точками планеты с использованием координат, присутствуют следующие величины (известные из математики):
- d – центральный угол (перпендикуляр) между двумя данными точками, лежащими на большом круге (т. е. на окружности, получаемой при сечении центральной части шара плоскостью);
- r – радиус сферы (т. е. усредненное значение радиуса Земли: 6372.795 км);
- y₁ и y₂ – широта двух точек в радианах;
- x₁ и x₂ – долгота двух точек в радианах.
Получим следующую тригонометрическую формулу, плавно вытекающую из теоремы пифагора (евклидова геометрия), которая равна:
cos(d) = sin(y₁)·sin(y₂) + cos(y₁)·cos(y₂)·cos(x₁ − x₂)
Данное соотношение можно получить из прямоугольного треугольника.
Подставив в формулу заданные значения точек, и получим вычисление.
Для того чтобы найти ответ про расстояние между двумя точками координат в километрах, поможет формула:
Способы решения и нахождения расстояния между точками по координатам
Чтобы провести решение и получить ответ о расстоянии точек в пространстве или плоскости по координатам GPS, необязательно использовать формулу вручную. Ответ о расстоянии между точками по координатам получим при помощи специальных утилит.
Онлайн-калькулятор для расчета расстояния между точками по координатам
В интернете есть множество сайтов с однотипными формулами в онлайн-калькуляторах для решения и нахождения прямого расстояния между двумя точками по координатам. Для этого нужно узнать широту и долготу двух искомых точек в пространстве или на плоскости и вбить эти данные в соответствующие окошки формулы (чем больше знаков после запятой у каждой точки известно, тем точнее получим значение).
Картографическая программа для нахождения расстояния между точками
Вычислять расстояние между двумя точками на плоскости по координатам и давать точный ответ умеет любое приложение-навигатор и без вычисления по формуле, например:
- «Карты»;
- «Google.Maps»;
- «Google Планета Земля»;
- «SAS.Планета».
 Определение координат объекта в Google Maps на компьютере не по формуле
Определение координат объекта в Google Maps на компьютере не по формуле
Для определения расстояния между точками не по дорогам и маршрутам, а напрямую по двум точкам, применяется инструмент «Линейка».
Многие из популярных навигаторов способны определять расстояние по координатам двух точек онлайн без формул: это можно сделать на сайте в разделе «Азимут» или «Другие вычисления».
На заметку. Наиболее точные данные между точками предоставляют материалы и таблицы кадастровых справочников, но также в них много информации, лишней для обычного пользователя.
Откуда берется погрешность при расчете расстояния между точками
При вычислении прямого расстояния между координатами двух точек применяется подсчет длины дуги этих точек, для чего берется радиус точек (его приблизительное среднее значение ввиду особенностей формы Земли). Из-за этого возникает погрешность, т. е. мы получим не точную информацию о расстоянии между точками.
Чем больше искомое расстояние, тем больше получим погрешность в расстоянии между точками.
Также неточность между точками получим тогда, когда при вычислениях расстояния между точками берут недостаточно цифр после запятой в координатах: результат будет приблизительным.
Так, между любыми двумя известными точками на чертеже Земли можно проложить как обычное расстояние по дорогам, так и прямую линию, которая соединяет каждую точку. Вычисления точек проводят вручную или автоматически, причем во втором случае даже будет известна возможная погрешность, которую получим при нахождении расстояние между точками, неизбежная при измерении сферы Земли.
Источник
С помощью карты можно определять расстояние между точками на земной поверхности, но точность таких вычислений невысока.
Ситуация относительно проста, если точки лежат на одном меридиане. Все меридианы имеют одинаковую длину. Можно подсчитать, что одному градусу широты соответствует примерно 111,3 км реальной длины. Поэтому надо найти разницу в долготе между точками и умножить ее на 111,3 км. Например, если точка А находится на северной широте 50°, а Б располагается на северной широте 32°, и при этом у них совпадает долгота, то расстояние между ними составит.
111,3х(50° – 32°) = 111,3х16 = 1780,8 км
Ситуация меняется, когда одна точка имеет северную, а другая – южную широту. В этом случае широты уже надо складывать. Так, если бы точка Б из предыдущего примера располагалась бы на южной широте 32°, то расстояние от А до Б составило бы:
111,3х(50° + 32°) = 111,3х82 = 9126,6 км
Ситуация усложняется, когда точки находятся на разных меридианах, но на одной параллели. Если у обеих точек долгота западная (или, наоборот, восточная), то сначала надо найти разницу их долгот. Если же одна точка имеет восточную, а другая западную долготу, то их надо суммировать. Далее результат надо умножить на длину 1° параллели. Эта длина у параллелей различна и зависит от их широты. Можно воспользоваться таблицей ниже:
| Широта параллели | Длина ее дуги величиной в 1° |
|---|---|
| 0° | 111,3 |
| 5° | 110,9 |
| 10° | 109,6 |
| 15° | 107,6 |
| 20° | 104,6 |
| 25° | 102,1 |
| 30° | 96,5 |
| 35° | 91,3 |
| 40° | 85,4 |
| 45° | 78,8 |
| 50° | 71,7 |
| 55° | 64,0 |
| 60° | 55,8 |
| 65° | 47,2 |
| 70° | 38,2 |
| 75° | 28,9 |
| 80° | 19,4 |
| 85° | 9,7 |
| 90° | 0 |
Например, нужно найти расстояние между точками, имеющими координаты:
А – 60° с. ш, 39° з. д.
Б – 60° с. ш, 25° з. д.
Широты у них одинаковы, поэтому смотрим на долготу. Она у обеих точек западная, поэтому надо найти их разницу:
39° – 25° = 14°
Полученный результат надо умножить на длину 1° параллели, широта которой составляет 60°. По табличке определяем, что на широте 60° дуга в 1° имеет длину 55,8 км. Перемножаем два числа:
14°х 55,8 км = 781,2 км
Список использованных источников
• https://www.yaklass.ru/p/geografiya/5-klass/izobrazheniia-zemnoi-poverkhnosti-i-ikh-ispolzovanie-131512/geograficheskie-koordinaty-161116/re-d77ff3cc-0858-4fd8-aabd-69f1fdffb41d • https://interneturok.ru/lesson/geografy/5-klass/plan-i-karta/gradusnaya-setka-geograficheskaya-dolgota-i-shirota

Гугломаг
Спрашивай! Не стесняйся!
Задать вопрос
Не все нашли? Используйте поиск по сайту
Как определить расстояние до объекта
Умение определять расстояние до объектов на местности может пригодиться в самых различных ситуациях. Для точного и быстрого определения расстояния существуют специальные приборы (дальномеры, шкалы биноклей, прицелы и стереотрубы). Впрочем, даже не имея специальных приспособлений, вы можете научиться узнавать расстояние при помощи самых простых подручных средств.

Вам понадобится
- Спичечный коробок, карандаш, линейка
Инструкция
Самый нехитрый способ определить расстояние на местности связан с использованием глазомера. Главное тут – натренированная зрительная память и умение мысленно отложить на видимой местности постоянную меру длины, например, 50 или 100 м. Закрепите в памяти эталоны и при необходимости сравните с ними то расстояние, которое вам необходимо измерить на местности. Один из самых простых эталонов – расстояние между столбами линии электропередач, которое составляет обычно около 50 м.
Измеряя расстояние посредством мысленного откладывания постоянной меры, учитывайте, что местные предметы будут казаться уменьшенными в зависимости от их удаления. Иными словами, при удалении в два раза предмет покажется в два раза меньше.
При использовании глазомера имейте ввиду, что в условиях недостаточной видимости (в тумане, в сумерки, пасмурную погоду, при дожде и т.п.) предметы кажутся расположенными дальше, чем есть на самом деле. Точность такого способа, прежде всего, зависит от тренированности наблюдателя. Обычная ошибка на километр составляет около 15%.
Используйте способ определения расстояний по линейным размерам. Для этого возьмите линейку и держите ее на расстоянии вытянутой руки. Измерьте по линейке в миллиметрах видимую ширину (высоту) объекта, до которого измеряете расстояние. Действительную ширину (высоту) предмета, известную вам, переведите в сантиметры, затем разделите на видимый размер в миллиметрах, а результат умножьте на 6 (постоянная величина). Получившийся результат будет искомым расстоянием до объекта.
Третий способ определить расстояние на местности – по угловой величине. Для этого требуется знать линейную величину объекта (длину, высоту или ширину), а также угол в тысячных, под которым виден наблюдаемый объект. Располагая такими данными, определите расстояние до объекта по формуле:D = L х 1000 / A;где D — расстояние до объекта; L — линейная величина объекта; A — угол, под которым видна линейная величина объекта; 1000 — постоянная величина.
Для определения угловой величины следует знать, что отрезку длиной 1 мм, расположенному на расстоянии 50 см от глаза, будет соответствовать угол в 2 тысячных. Соответственно, для отрезка в 1 см угловая величина будет равна 20 тысячных и так далее. Запомните угловые величины (в тысячных) некоторых подручных средств:Большой палец руки (толщина) – 40;
Мизинец (толщина) – 25;
Карандаш – 10-11;
Спичечная коробка (ширина) – 50;
Спичечная коробка (высота) – 30
Спичка (толщина) – 2.
Источники:
- Определение расстояний на местности
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Сколько до центра?
К.С. ЛАЗАРЕВИЧ
Земля имеет форму шара. Эта истина должна быть
для географов непреложной, несмотря ни на какие
разговоры о сплющенности Земли у полюсов. Глобус
с диаметром, равным высоте классной комнаты,
нужно придавить с каждого полюса лишь на
полсантиметра, чтобы показать эту сплющенность.
Разрез Земли, изображенный на тетрадном листе
(примем экваториальный диаметр равным 150 мм),
касаясь у экватора проведенной циркулем
окружности, у полюсов будет отходить от нее на 0,25
мм, то есть примерно на толщину линии самой этой
окружности. Географические процессы во многом
обусловлены формой Земли (зональность, общая
циркуляция атмосферы), но именно ее
шарообразностью, на сплюснутость же не реагируют
совершенно.
Когда же пришла пора измерять Землю, строить
точные карты, — вот тут-то эта сплющеннось и
проявилась. Форма планеты не может быть точно
описана математической формулой. Пришлось
подбирать геометрическое тело, которое может
быть охарактеризовано более или менее простой
формулой и наиболее близко напоминает форму
Земли. Это — эллипсоид вращения, то есть тело,
которое образуется в результате вращения
эллипса вокруг одной из его осей. Земля
вращается, поэтому ось вращения эллипса
совместили с осью Земли. Так как Земля сплюснута
у полюсов, вращать эллипс стали вокруг его
короткой оси.
Измерение Земли очень сложно, у разных ученых
получаются разные результаты; в России
применяется эллипсоид, вычисленный в 1940 г.
Феодосием Николаевичем Красовским. Малая
полуось эллипсоида Красовского (расстояние от
центра до полюса)
Rp = 6 356 853 м,
большая полуось (от центра до экватора)
Re = 6 378 245 м.
Поверхность эллипсоида Красовского не более
чем на первые десятки метров отстоит от уровня
океана, форму которого принимают за истинную
форму Земли. Поэтому все вычисления будем вести
относительно эллипсоида.
Итак, полярный радиус земного эллипсоида на
21 392 м короче экваториального; экватор отстоит
от центра Земли примерно на 21,4 км дальше, чем
полюс. Это значит, что вершина горы с абсолютной
высотой (Н) 1 км на полюсе будет на 19,4 км ближе к
центру Земли, чем дно ямы такой же глубины (здесь
Н будет отрицательной величиной) на экваторе.
Расстояние R0 поверхности эллипсоида от
центра Земли на произвольной широте
определяется по формуле.
Для любителей математики приводим эту формулу:
![]() ,
,
где Re — экваториальный радиус земного
эллипсоида,
Rp — полярный радиус земного эллипсоида,
![]() — широта
— широта
места.
Нетрудно увидеть, что для полюса R0 = Rp,
для экватора R0 = Re.
Чтобы определить, на каком расстоянии от центра
Земли находится та или иная точка реальной (то
есть со всеми горами и впадинами) земной
поверхности, а также любая точка над или под
поверхностью, нужно прибавить к расстоянию R0
абсолютную высоту точки; не следует забывать, что
это сложение — алгебраическое, ведь
абсолютная отметка может быть и отрицательной.
Многозначные числа при сравнении не так
наглядны, как короткие, поэтому отсчет будем
производить не от центра Земли, а от того
расстояния, на которое отстоит от него уровень
моря на полюсе.
Сплюснутость Земли вносит довольно
существенные поправки в расстояние точек от
центра Земли. Казалось бы, дальше всего от центра
должна отстоять высочайшая вершина Земли, а
ближе всего к нему должно быть дно самой глубокой
океанической впадины. Ничуть не бывало. Уровень
моря, от которого отсчитывают глубину Марианской
впадины, отстоит от центра Земли почти на 20 км
дальше, чем в Гренландском море, и дно вдвое более
глубокого Марианского жёлоба оказывается на
15,5 км дальше от центра, чем самая глубокая
точка Гренландского моря (таблица). Гора
Чимборасо находится почти на экваторе, уровень
моря там отстоит от центра Земли на 4,7 км дальше,
чем на широте Джомолунгмы, которая, несмотря на
то, что на 2,5 км выше, проигрывает в расстоянии от
центра более чем на 2 км.
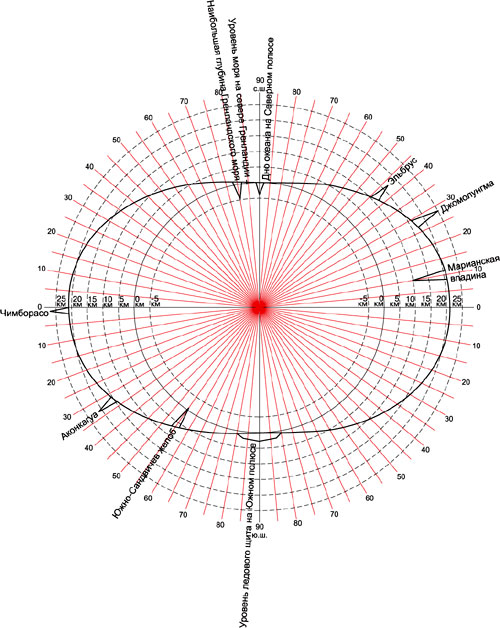
На рисунке окружности показывают равные
расстояния от центра Земли, они проведены через 5
км. Только масштаб резко преувеличен (примерно в
160 раз по сравнению с масштабом радиуса Земли),
иначе, как мы уже успели убедиться, никакой
разницы в расстояниях видно не будет. Жирной
линией проведена поверхность эллипсоида. То, что
масштаб радиуса Земли и масштаб неровностей на
шаре сильно различаются, вызывает искажение
фигуры, получился уже не эллипсоид, а некая хоть и
симметричная, но неправильная фигура, у полюсов
можно даже заметить некоторую вогнутость.
На полюсах и на экваторе поверхность
эллипсоида параллельна окружностям, при
отклонении на 1° широты ее расстояние от центра
Земли меняется на какие-нибудь два десятка
метров. В средних же широтах, около 45°,
поверхность эллипсоида пересекает окружности
под большим углом (впрочем, он кажется большим
только при резко преувеличенном масштабе, на
самом деле это 5—6 угловых секунд), и при
изменении широты на 1° расстояние эллипсоида от
центра Земли меняется без малого на 400 м. Резкая
разница на чертеже в масштабах радиуса Земли и
приповерхностной ее части приводит к тому, что
направление к центру Земли в средних широтах
оказывается не перпендикулярным к поверхности
эллипсоида, поэтому горы и впадины кажутся
наклоненными.
Таким образом, самая близкая к центру Земли
точка поверхности литосферы совпадает с
наиболее глубокой точкой дна Гренландского моря,
а самая дальняя — вершина горы Чимборасо.
Возможно, в справочных материалах вы найдете
цифры, несколько отличающиеся от приведенных
здесь; это можно объяснить тем, что при одних
вычислениях за нуль принимался уровень моря, при
других — эллипсоид Красовского, при третьих —
какой-то из эллипсоидов, принятых в других
странах (например, эллипсоид Бесселя).
Если же захотите узнать, на каком расстоянии от
центра Земли находится любая точка, широту и
абсолютную отметку которой вы знаете, вычислите R0
по формуле и прибавьте абсолютную отметку.
Сложно? Тогда воспользуйтесь чертежом. По нему
можно с точностью, которая вполне
удовлетворительна, найти, насколько на каждой
широте поверхность эллипсоида отстоит дальше от
центра Земли, чем уровень моря на полюсе.
Прибавьте к этой величине абсолютную отметку
точки (или отнимите, если она отрицательна). К
полученному результату прибавьте полярный
радиус Земли — 6 356,85 км.
Формулу для расчета вывел
сотрудник редакции газеты «Математика»
В.М. Бусев
Статья подготовлена при поддержке ассоциации преподавателей «Огни МГУ». На сайте ассоциации преподавателей «Огни МГУ», расположенным по адресу «Repetitor-MGU.Ru», вы сможете воспользоваться услугой «репетитор по математике», которая позволит восполнить пробелы с учебой или подготовиться к экзамену по математике. В ассоциации состоят высококвалифицированные преподаватели первого университета Москвы – МГУ. Первое занятие с репетитором бесплатное.
Таблица
Расстояние от центра Земли
некоторых характерных точек поверхности
литосферы
по сравнению с полярным радиусом
| Название точки | Широта места | R0–Rp, м |
H, м | R0–Rp+H, км | |
| Наибольшая глубина Гренландского моря |
80° | с. | 785 | –5 527 | –4,74 |
| Дно океана на Северном полюсе | 90° | с. | 0 | –4 316 | –4,32 |
| Южно-Сандвичев желоб | 55° | ю. | 7 020 | –8 325 | –1,30 |
| Уровень моря на севере Гренландии (самая северная точка суши) |
84° | с. | 233 | 0 | 0,23 |
| Уровень льда на Южном полюсе | 90° | ю. | 0 | 2 800 | 2,80 |
| Марианская впадина | 10° | с. | 20 730 | –11 022 | 9,71 |
| Эльбрус | 43° | с. | 11 410 | 5 642 | 17,05 |
| Аконкагуа | 33° | ю. | 15 024 | 6 960 | 21,98 |
| Джомолунгма | 28° | с. | 16 650 | 8 848 | 25,50 |
| Чимборасо | 1° | ю. | 21 370 | 6 310 | 27,68 |
Расстояние от центра Земли
некоторых точек поверхности литосферы