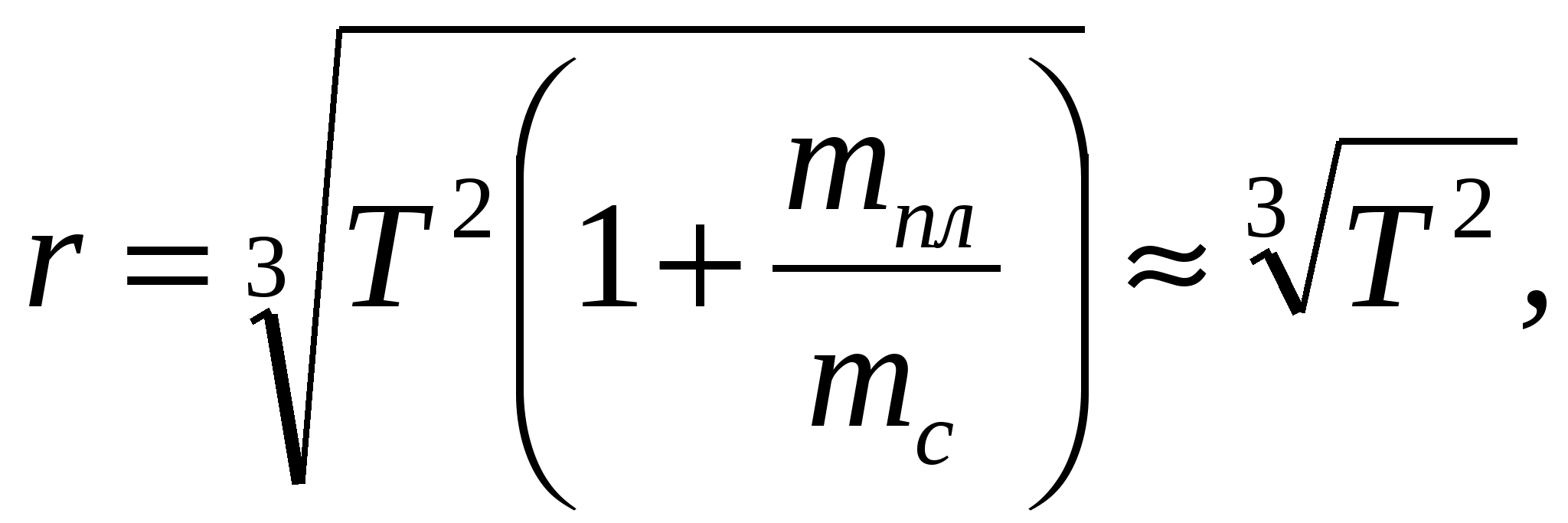Как найти расстояние от звезды до планеты

Как вычислить расстояние от звезды до планеты

В этой статье мы расскажем о самых известных методах вычисления расстояния между звездой и планетой. Вы узнаете о технологиях, которые позволяют астрономам измерять расстояния на многие световые годы за пределами нашей галактики.

Триангуляция

Одним из наиболее распространенных методов определения расстояния является триангуляция. Этот метод основан на знании углов звезды и нескольких точек на Земле, с помощью которых можно вычислить расстояние.

Для этого астрономы детально изучают траекторию звезды на небесной сфере и постоянно фиксируют ее местоположение на разных временных отрезках. Затем они измеряют углы между звездой и точками на Земле, используя телескопы и другие инструменты. После этого они применяют треугольную теорему, чтобы определить расстояние.

Триангуляция является точным методом, но он требует точных измерений и может быть ограничен тем, что некоторые звезды не могут быть наблюдаемы на Земле.

Закон Большого Взрыва

Другой метод измерения расстояния между звездой и планетой основан на изучении космической структуры и обратного пути света, который излучается из звезды. Закон Большого Взрыва позволяет узнать, насколько звезда далека.

Когда свет из звезды проходит через космический вакуум, его длина волны изменяется. Это связано с тем, что космический материал влияет на свет, заставляя его изменять свое направление. Если мы можем измерить изменение длины волны света, мы можем определить, сколько световых лет далека звезда.

Измерение этого изменения длины волны может быть сложным и требует технологических усилий. Однако эта методика может использоваться для измерения очень дальних звезд за пределами нашей галактики.

Червоточинная метрика

Эта методика основана на теории общей теории относительности, разработанной Альбертом Эйнштейном. Он предложил использовать пространство-время, чтобы определить, насколько звезда далека.

Идея заключается в том, что масса и сила притяжения звезды изменяют форму пространства-времени вокруг нее. Когда проходит свет, он не проходит в одинаковых условиях, что влияет на быстроту его распространения. Если мы можем измерить это изменение скорости света, мы можем определить, насколько звезда далека.

Чтобы применить этот метод, астрономы измеряют изменение цвета света, излучаемого звездой, и анализируют его в свете изменений, которые происходят в пространстве-времени вокруг звезды.

Итог

Вычисление расстояния между звездой и планетой может быть сложным заданием, но благодаря новым технологиям и методам мы можем измерять расстояния на многие световые лета. Триангуляция, Закон Большого Взрыва и червоточинная метрика — это некоторые из самых известных и точных методов измерения расстояния в космосе.

• Триангуляция основана на знании углов звезды и нескольких точек на Земле.
• Закон Большого Взрыва позволяет узнать, насколько звезда далека, используя измерение космической структуры.
• Червоточинная метрика основана на теории общей теории относительности.

Изучение космоса — это процесс, требующий много технологических усилий, но технологии и методы, которые используются для измерения расстояний в космосе, могут помочь узнать о нашей вселенной намного больше, чем мы могли предположить.

Как вычислить расстояние от звезды до планеты

Космическое пространство по-прежнему остается мистическим и недоступным предметом для обычных людей. Но с развитием технологии, мы можем лучше понимать космос и то, что находится там. Каждый день астрономы по всему миру работают над поиском ответов на вопросы, которые терзают человечество в течение многих веков. Путешествия в космос вызывают особое внимание у всего человечества и вычисление расстояния от звезды до планеты — одно из таких заданий.

Как узнать расстояние до Марса?

Перед тем, как вычислить расстояние от звезды до планеты, нам нужно понять, как оно вычисляется. Начнем с расстояния от Земли до Марса.

“Расстояние от Земли до Марса зависит от позиций планет около Солнца. В результате орбит Земли и Марса, расстояние между ними постоянно меняется. Хотя расстояние может быть от 34 миллионов до 140 миллионов миль.”

Как можно узнать максимально точное расстояние? Тут обычно используется среднее расстояние от Земли до Марса в момент, когда они находятся ближе всего и дальше всего друг от друга. В результате этого расчета, получается, что среднее расстояние между Землей и Марсом составляет примерно 48,6 миллионов миль.

Как вычислить до других планет?

Чтобы вычислить расстояние до других планет, мы должны использовать ту же самую логику как и с Марсом. Оно может быть менее точным, но все же поможет нам приблизительно понять, в какой точке космического пространства находятся объекты.

• Меркурий ближе всего к Солнцу, и среднее расстояние между Меркурием и Землей составляет примерно 48 миллионов миль.
• Венера следующая планета от Солнца, и среднее расстояние между ней и Землей составляет примерно 26 миллионов миль.
• Марс, как мы уже знаем, находится на расстоянии около 48,6 миллионов миль от Земли.
• Юпитер, самая большая планета в нашей Солнечной системе, расположена примерно на расстоянии 390 миллионов миль от Земли.
• Сатурн находится еще дальше, приблизительно на расстоянии 792 миллионов миль от Земли.
• Уран – газовый гигант следующий после Сатурна, и расстояние между Ураном и Землей составляет примерно 1,7 миллиарда миль.
• Нептун, последняя планета нашей Солнечной системы, находится еще дальше, примерно на расстоянии 2,8 миллиарда миль от Земли.

Какими инструментами можно измерить расстояние?

Существует несколько способов, с помощью которых можно узнать расстояние до звезды или планеты. Один из наиболее точных методов — измерение изменения положения звезд против звездного фона.

Другой метод – параллаксный метод, это точный и простой способ оценить расстояние. Он основан на том, что объект кажется смещенным на некоторую величину, когда мы смотрим на него из разных точек. Этот метод использует разность параллакса, чтобы определить расстояние.

Еще один способ – получить информацию от радаров. Приемник радиоволн позволяет измерять расстояние от объекта, в передаче которого мы заинтересованы. Этот метод лучше всего подходит для обнаружения маленьких тел в Космосе, например, астероидов и комет.

Окончание

Как мы видим, не существует одного способа, с помощью которого можно точно измерить расстояние от звезды до планеты. Но с помощью использования вышеописанных методов, астрономы и ученые могут получить оценку расстояния от объектов во Вселенной. И знание того, как это делается, является важным шагом в проникновении в тайны космического пространства и ответом на вопросы людей, которые интересуются областью астрономии и космических исследований.

Как вычислить расстояние от звезды до планеты

Изучение космоса — это одно из самых интересных занятий. Люди за всю свою историю всегда уважали и боялись необъяснимых явлений в космическом пространстве. Сегодня мы поговорим об одном из таких явлений — о расстоянии между звездой и планетой. Как его измерить? Стоит ли на такие изыскания тратить время и ресурсы?

Как измерять расстояние?

Все начинается с того, что нужно точно измерить угловую величину движения объекта на небесной сфере. Это можно сделать, используя метод параллакса. Параллакс — это разность показаний зрительных приборов, если они смотрят на один объект с двух разных мест на земной поверхности. Простыми словами, это смещение звезды относительно фона звезд, вызванное различием в положении наблюдателей.

Далее, по формуле параллакса, можно определить расстояние до объекта. Для этого используется основание — расстояние между наблюдателями. Если оно известно, можно легко вычислить искомое расстояние до звезды. Но основание — это тоже не так просто измерить. Поэтому существует как обзорные, так и точные методы исследований, которые помогают определить основание с большей точностью.

Когда стоит заниматься вычислениями?

Вычисление расстояния до звезды — это длительный и трудоемкий процесс. Поэтому, прежде чем браться за его проведение, необходимо принимать во внимание ряд факторов, которые могут повлиять на результаты исследования.

• Требуется ли точный результат?
• Находится ли исследуемая планета внутри нашей галактики?
• Какие затраты следует вложить в исследование?

Ответы на эти вопросы помогут проанализировать стратегию и прийти к другим выводам. Например, если точности вычисления не так уж и требуется, можно обойтись обзорными методами и проверять только приблизительное расстояние до объекта.

Заключение

Вычисление расстояния до звезды или планеты — это длительный и трудоемкий процесс. Но если учесть все факторы и выбрать наиболее эффективную стратегию, можно достигнуть впечатляющих результатов. Таким образом, научное исследование космического пространства не только интересно, но и полезно для развития нашей цивилизации.

Примечание: анимационный ролик в конце статьи. Там все ясно.

Определение расстояния в Космосе является неотъемлемой частью развития астрономии. Для астрономов вопрос точности измерения стоит в первых рядах.

Например, человечество узнало, что несколько миллиардов лет назад Вселенная расширялась гораздо медленнее, чем сейчас. Тем самым, выяснив, что воздействие темной энергии постепенно возрастает.

Да и к тому же важно знать своё место во Вселенной. Ради улучшения способов учёные со всего света слетаются каждое десятилетие.

В последний раз астрономы встретились на 30-й конференции Международного астрономического союза, которая прошла в августе 2018-го года в Вене. В статье рассказано о четырех методах определения расстояния в космическом пространстве.

1. Метод локации

Метод локации эффективен для измерения расстояний до объектов, расположенных в пределах Солнечной системы. Суть в следующем: лазер излучает свет в сторону нужного космического объекта.

На этом объекте, к примеру Луна, установлены специальные уголковые отражатели, благодаря которым падающий луч света отражается точно в сторону источника излучения. Зная скорость света, а также время полёта, простой формулой определяется расстояние.

Благодаря этому способу человечество узнало удалённость Земли от Луны с погрешностью до одной десятой сантиметра. Уголковые отражатели на Луне были доставлены как советскими луноходами, так и американскими астронавтами миссии “Аполлон”.

Впоследствии учёные определили, что каждый год Луна отдаляется от Земли на 3 – 4 сантиметра именно с помощью метода лазерной локации. Стоит учесть, излучение необязательно должно быть в световом (видимом) диапазоне.

Теоретически, этим способом можно точно измерить расстояние между Землёй и Плутоном. Свету потребуется всего лишь 11 часов, чтобы долететь до карликовой планеты и вернуться назад.

Конечно, вряд ли там когда-нибудь установят отражатели. Да и ни к чему они, так как для этого существуют космические аппараты, которые, пролетая мимо планет, отправляют снимки со скоростью света в родную гавань.

К примеру, в июле 2015-го космический аппарат “Новые горизонты”, во время пролёта, максимально сблизился с Плутоном на расстоянии в 12500 км, отправив впечатляющие снимки карликовой планеты Земле.

Как указано выше, у этого метода есть предел. Если ближайшая звезда к Земле, (не считая Солнца), Проксима Центавра удалена на расстоянии в 4.22 светового года, то самому быстрому аппарату “Вояджер-1”, скорость которого составляет 17 км/с относительно Солнца, понадобится 75 000 лет.

Да и чем дальше объект, тем сложнее идентифицировать то самое отражённое излучение. Поэтому метод лазерной локации подходит только для Солнечной системы. Значит пора перейти ко второму.

2. Метод годичного параллакса

(в ролике нагляднее — прим. автора)

Этот метод дает обширные возможности для определения расстояния до звёзд. Сначала разберёмся со словом параллакс. Параллакс — смещение близкого объекта относительно удалённого при наблюдении с разного местоположения. Чем больше смещение, тем ближе объект.

С явлением параллакс мы встречаемся повседневно и в обычной жизни. Например, когда мы смотрим в окно при передвижении на поезде, то замечаем, что более близкие деревья или кустарники смещаются гораздо быстрее по сравнению с удалёнными.

Так как звёзды находятся слишком далеко, то эффект параллакса на Земле незаметен. Но здесь на помощь приходит естественное движение планеты вокруг Солнца. Тут уже можно наблюдать необходимую звезду в пределах 300 миллионов км.

Сам годичный параллакс представляет собой угол, вершиной которого является звезда (не Солнце). Угол образован между двумя сторонами. Чем меньше угол, тем дальше объект.

Первая сторона: расстояние между необходимой звездой и Солнцем. Вторая: расстояние между той же звездой и Землёй. Получается треугольник, у которого третья сторона не что иное, как радиус земной орбиты, равный 1 астрономической единице.

По сути, для определения угла до нужной звезды достаточно годовое наблюдение, так как Земля совершает полный оборот за это время. Отсюда и пошло название годичного параллакса.

Другой причиной круглогодичного непрерывного наблюдения является корректировка движения удалённых звёзд и самого Солнца вокруг центра Млечного Пути. Ведь всё движется во Вселенной.

Для определения расстояния обычно используют прямоугольный треугольник. Причём прямой угол может быть как у Земли, так и у Солнца. В основном это зависит от расположения наблюдаемой звезды относительно Солнечной системы.

Если звезда ближе к эклиптике, то прямой угол берётся у Земли. Если ближе к перпендикуляру Солнечной системы, то у Солнца. Всё же треугольник необязательно должен быть прямоугольным.

В случае с обычным треугольником расстояние от Земли до звезды определяется теоремой синусов, где стороны любого треугольника пропорциональны синусам противолежащих углов. В общем, метод годичного параллакса — обычная тригонометрия.

Но и здесь есть ограничения. Дело в том, что даже Проксима Центавра находится на расстоянии, годичный параллакс которого равен 0,75 угловой секунды.

Немного об угловой секунде. Представим 1 угловой градус. Этот градус состоит из 60-ти угловых минут, а минута из 60-ти угловых секунд. То есть 1 угловая секунда — это всё равно что смотреть на человеческий волос с расстояния в 20 метров, толщина которого 0,1 мм.

Мы не способны видеть объекты при таком разрешении. Астрономы даже придумали термин, состоящий из двух слов: параллакс + секунда = парсек, который обозначает расстояние до объекта, годичный параллакс которого равен одной угловой секунде.

Даже ближайшие звёзды расположены дальше 1 парсека, не говоря уж об отдалённых. Благодаря современным приборам человечество научилось измерять расстояния до звёзд этим методом. Но учёные пошли дальше.

В конце 2013 года Европейское Космическое Агентство запустило космический аппарат “Gaia”, который движется по орбите вокруг Солнца в полутора миллионов км от Земли. Точность аппарата составляет 25 микросекунд дуги. Это всё равно что разглядеть с Земли двухрублёвую монету на Луне.

В общем, “Gaia” способен определять расстояния практически до любых звёзд нашего Млечного Пути. Но здесь наступает предел. Расстояния до других галактик измеряются следующим способом.

3. Метод звёздных маяков

Для удобства измерения выбирают звёзды цефеиды. Их ещё называют звёздными маяками. Цефеиды — переменные звёзды, в которых происходит изменение светимости строго с определённым периодом. Период обычно составляет от 1 до 50 суток. Светимость меняется из-за изменения размера Цефеиды.

В 20-м веке в Гарвардской обсерватории состоялось прорывное открытие. Установлена связь между периодом изменения яркости Цефеиды и абсолютной звёздной величиной.

Астрономами было установлено, что абсолютная звёздная величина соответствует видимой на расстоянии в 10 парсек или 32.6 светового года. Величину на таком расстоянии измеряли годичным параллаксом различных ближайших переменных звёзд. То есть предыдущий метод является также калибровочным, благодаря которому установили абсолютную звёздную величину.

У Солнца, например, абсолютная звёздная величина +4.8, у Веги 0,5. Всё что выше + 6, недоступно человеческому глазу с расстояния в 10 парсек.

Зная период пульсаций Цефеиды, определяется абсолютная звёздная величина, с помощью которой, в сравнении с видимой, измеряется расстояние.

С помощью цефеид человечество узнало удалённость миллионов галактик. Но чтобы измерить расстояние до галактик, расположенных в миллиардах световых годах, астрономы полагаются на более яркий метод.

4. Вспышка Сверхновой звезды

Между яркостью и расстоянием есть определённая зависимость. К примеру, возьмём обычную свечу. Если первый объект находится в 2 раза дальше второго от источника освещения, то светового потока будет приходиться на первый объект в 4 раза меньше. То есть зависимость между яркостью и расстоянием обратно квадратичная.

Чем дальше объект, тем сложнее обнаружить его светимость. Но Вселенная часто помогает вспышками сверхновых звёзд, которые рождаются в среднем 1 раз в 100 лет в галактике. В настоящее время считается, что в Наблюдаемой Вселенной около 2 триллионов галактик. Конечно, на самом деле их больше, но пока столько.

Значит, теоретически, каждую секунду вспыхивают 634 сверхновые звёзды. Когда взрывается сверхновая, она выделяет энергию, сопоставимую с энергией 10-миллиардного жизненного цикла Солнца.

То есть Солнце прожило полжизни. За 5 миллиардов лет выделило в космическое пространство энергию аналогичную половине энергии вспышки Сверхновой. Вспышки Сверхновых — это подарок Вселенной для измерения расстояний.

Заключение

Стоит отметить, что чем дальше объект, тем труднее точно измерить расстояние. Дело в том, что расчёты неидеальны, так как для этого нужен 100%-й вакуум в космическом пространстве, которого нигде нет, а Вселенная должна оставаться неподвижной.

Также излучение удалённого объекта рассеивается не только космической пылью, но и тёмной материей, которую учёным пока что обнаружить не удалось, хоть и доказано, что она существует.

Ещё отклонение в расчётах вызывают массивные объекты, которые согласно Общей Теорией Относительности Эйнштейна искривляют траекторию излучения.

Однако учёные не останавливаются на достигнутом, продолжают встречаться и изобретать более совершенные методы и приборы.

Приятного просмотра:

Определение расстояний до звезд и планет

http://monax.ru/order/ – рефераты
на заказ (более 2300 авторов в 450 городах
СНГ).

Содержание:

Вступление. 3

Определение расстояний до
космических объектов. 3

Определение
расстояний до планет. 4

Определение
расстояний до ближайших звезд. 4

Метод параллакса. 4

Фотометрический метод
определения расстояний. 6

Определение расстояния по
относительным скоростям. 7

Цефеиды. 8

Список литературы. 9

Вступление.

Наши знания о Вселенной тесно
связаны со способностью человека
определять расстояния в пространстве.
С незапамятных времен вопрос «как
далеко?» играл первостепенную роль для
астронома в его попытках познать свойства
Вселенной, в которой он живет. Но как бы
ни было велико стремление человека к
познанию, оно не могло быть осуществлено
до тех пор, пока в распоряжении людей
не оказались высокочувствительные и
совершенные инструменты. Таким образом,
хотя на протяжении веков представления
о физическом мире непрерывно развивались,
завесы, скрывавшие верстовые столбы
пространства, оставались нетронутыми.
Во все века философы и астрономы
размышляли о космических расстояниях
и усердно искали способы их измерения.
Но все было напрасно, так как необходимые
для этого инструменты не могли быть
изготовлены. И, наконец, после того как
телескопы уже в течение многих лет
использовались астрономами и первые
гении посвятили свой талант изучению
богатств, добытых этими телескопами,
настало время союза точной механики и
совершенной оптики, который позволил
создать инструмент, способный разрешить
проблему расстояний. Барьеры были
устранены, и многие астрономы объединили
свои знания, мастерство и интуицию с
целью определить те колоссальные
расстояния, которые отделяют от нас
звездные миры.

В 1838 году три астронома (в разных
частях света) успешно измерили расстояния
до некоторых звезд. Фридрих Вильгельм
Бессель в Германии определил расстояние
до звезды Лебедь 61. Выдающийся русский
астроном Василий Струве установил
расстояние до звезды Веги. На мысе Доброй
Надежды в Южной Африке Томас Гендерсон
измерил расстояние до ближайшей к Солнцу
звезды – альфа Центавра. Во всех названных
случаях астрономы измеряли невообразимо
малое угловое расстояние, чтобы определить
так называемый параллакс. Их успех был
обусловлен тем, что звезды, до которых
они измеряли расстояния, находились
относительно близко к Земле.

Определение расстояний
до космических объектов.

В астрономии нет единого
универсального способа определения
расстояний. По мере перехода от близких
небесных тел к более далеким одни методы
определения расстояний сменяют другие,
служащие, как правило, основой для
последующих. Точность оценки расстояний
ограничивается либо точностью самого
грубого из методов, либо точностью
измерения астрономической единицы
длины (а. е.), величина которой по
радиолокационным измерениям известна
со среднеквадратичной погрешностью
0,9 км. и равна 149597867,9 
0,9 км. С учетом различных изменений а.
е. Международный астрономический союз
принял в 1976 году значение 1 а. е. = 149597870
 2 км.

Определение
расстояний до планет.

С
реднее
расстояние r
планеты от Солнца (в долях а. е.) находят
по периоду ее обращения Т:

где
r выражено в а. е., а Т –
в земных годах. Массой планеты m
по сравнению с массой солнца m_>c>
можно пренебречь. Формула следует из
третьего закона Кеплера (квадраты
периодов обращения планет вокруг Солнца
относятся как кубы их средних расстояний
от Солнца).

Расстояния до Луны и планет с
высокой точностью определены также
методами радиолокации планет.

Определение
расстояний до ближайших звезд.

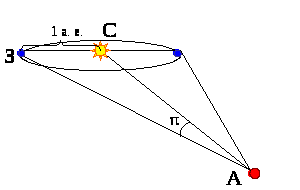
Метод параллакса.

Вследствие годичного движения
Земли по орбите близкие звезды немного
перемещаются относительно далеких
«неподвижных» звезд. За год такая звезда
описывает на небесной сфере малый
эллипс, размеры которого тем меньше,
чем звезда дальше. В угловой мере большая
полуось этого эллипса приблизительно
равна величине максимального угла, под
каким со звезды видна 1 а. е. (большая
полуось земной орбиты), перпендикулярная
направлению на звезду. Этот угол (),
называемый годичным или тригонометрическим
параллаксом звезды, равный половине ее
видимого смещения за год, служит для
измерения расстояния до нее на основе
тригонометрических соотношений между
сторонами и углами треугольника ЗСА, в
котором известен угол 
и базис – большая полуось земной орбиты
(см. рис. 1).

Расстояние r до звезды,
определяемое по величине ее
тригонометрического параллакса ,
равно:

r = 206265”/
(а. е.),

где
параллакс  выражен
в угловых секундах.

Рисунок 1. Определение расстояния до
звезды методом параллакса (А – звезда,
З – Земля, С – Солнце).

Для удобства
определения расстояний до звезд с
помощью параллаксов в астрономии
применяют специальную единицу длины –
парсек (пс). Звезда, находящаяся на
расстоянии 1 пс, имеет параллакс, равный
1”. Согласно вышеназванной формуле, 1
пс = 206265 а. е. = 3,086·10¹⁸ см.

Наряду с парсеком применяется
еще одна специальная единица расстояний
– световой год (т. е. расстояние, которое
свет проходит за 1 год), он равен 0,307 пс,
или 9,46·10¹⁷ см.

Ближайшая к Солнечной системе
звезда – красный карлик 12-й звездной
величины Проксима Центавра – имеет
параллакс 0,762, т. е. расстояние до нее
равно 1,31 пс (4,3 световых года).

Нижний предел измерения
тригонометрических параллаксов ~0,01”,
поэтому с их помощью можно измерять
расстояния, не превышающие 100 пс с
относительной погрешностью 50%. (При
расстояниях до 20 пс относительная
погрешность не превышает 10%.) Этим методом
до настоящего времени определены
расстояния до около 6000 звезд. Расстояния
до более далеких звезд в астрономии
определяют в основном фотометрическим
методом.

Таблица
1. Двадцать ближайших звезд.

№№ п. п.	Название звезды	Параллакс в секундах дуги	Расстояние, пс	Видимая звездная величина, m	Абсолютная звездная величина, М	Спек-траль-ный класс
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20	Солнце. . . . . . . . . Проксима Центавра . α Центавра А . . . . . α Центавра В . . . . . Звезда Барнарда . . . Лаланд 21185 . . . . . Вольф 359 . . . . . . . +36˚2147 . . . . . . . Сириус . . . . . . . . Спутник Сириуса . . Росс 154 . . . . . . . . Росс 248 . . . . . . . . Лейтен 7896 . . . . . ε Эридана . . . . . . . Процион . . . . . . . Спутник Проциона . . 61 Лебедя . . . . . . . Спутник 61 Лебедя . . τ Кита . . . . . . . . . ε Индейца . . . . . . .	–– 0,762 0,756 0,756 0,543 0,407 0,403 0,388 0,376 0,376 0,350 0,334 0,328 0,303 0,297 0,297 0,296 0,296 0,294 0,288	1/206256 1,31 1,32 1,32 1,84 2,46 2,48 2,58 2,66 2,66 2,86 2,99 3,05 3,30 3,37 3,37 3,38 3,38 3,40 3,47	–26,7 +11,3 +0,3 +1,7 +9,5 +10,7 +13,5 +7,5 –1,5 +8,5 +10,5 +12,2 +12,3 +3,8 +0,5 +10,8 +5,4 +6,1 +3,7 +4,7	+4,9 +15,7 +4,7 +6,1 +13,1 +13,7 +16,5 +10,4 +1,4 +11,4 +13,2 +14,7 +14,9 +6,2 +2,8 +13,1 +7,7 +8,4 +6,0 +7,0	G4 M G4 K1 M5 M2 M8 M2 A1 A5 M5 M6 M6 K2 G4 K3 K5 G5 K5

Фотометрический
метод определения расстояний.

Освещенности, создаваемые
одинаковыми по мощности источниками
света, обратно пропорциональны квадратам
расстояний до них. Следовательно, видимый
блеск одинаковых светил (т. е. освещенность,
создаваемая у Земли на единичной
площадке, перпендикулярной лучам света)
может служить мерой расстояния до них.
Выражение освещенностей в звездных
величинах (m – видимая звездная
величина, М – абсолютная звездная
величина) приводит к следующей основной
формуле фотометрических расстояний r_>ф>
(пс):

lgr_>ф> = 0,2 (m
– M) + 1.

При определении r_>ф >по
вышеназванной формуле погрешность
составляет ~30%.

Для светил, у которых известны
тригонометрические параллаксы, можно,
определив М по этой же формуле, сопоставить
физические свойства с абсолютными
звездными величинами. Это сопоставление
показало, что абсолютные звездные
величины многих классов светил (звезд,
галактик и др.) можно оценивать по ряду
их физических свойств.

Зная расстояния до некоторого
числа звезд, вычисленные методом
параллакса, можно было вычислить
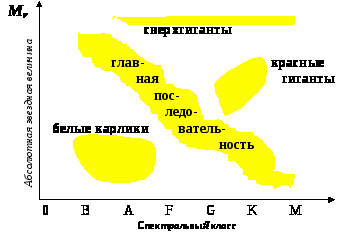
светимости и сопоставить их со спектром
тех же звезд, (см. рис. 2). Из диаграммы
видно, что каждому определенному
подклассу звезд (например A) соответствует
определенная светимость, таким образом,
достаточно точно определить спектральный
класс и можно выяснить ее светимость,
а следовательно, и расстояние.

Иногда определенному классу
соответствует другая светимость, но в
этом случае и спектр у них несколько
другой. Спектры карликов и гигантов
различаются интенсивностью определенных
линий или их пар, причем это отличие
можно выяснить, исследуя близко
находящиеся звезды. Это отличие связано
с тем, что атмосферы гигантов обширнее
и разреженнее. Точность определения
расстояния таким способом составляет
~20%.

Рисунок 2: диаграмма зависимости
спектрального класса от абс. звездной
величины (Герцшпрунга – Рессела)

Определение
расстояния по относительным скоростям.

Косвенным показателем расстояния
до звезд являются их относительные
скорости: как правило, чем ближе звезда,
тем больше смещается она по небесной
сфере. Определить таким способом
расстояние, конечно нельзя, но этот
способ дает возможность “вылавливать”
близкие звезды.

Также существует другой метод
определения расстояний по скоростям,
применимый для звездных скоплений. Он
основан на том, что все звезды, принадлежащие
одному скоплению, движутся в одном и
том же направлении по параллельным
траекториям. Измерив лучевую скорость
звезд с помощью эффекта Доплера, а также
скорость, с которой эти звезды смещаются
относительно очень удаленных, то есть
условно неподвижных звезд, можно
определить расстояние до интересующего
нас скопления.

Цефеиды.

Важный метод определения
фотометрических расстояний в Галактике
и до соседних звездных систем – галактик
– основан на характерном свойстве
переменных звезд – цефеид.

Первой из обнаруженных цефеид
была  Цефея, которая
меняла свой блеск с амплитудой 1,
температуру (на 800K), размер и спектральный
класс. Цефеиды – это неустойчивые звезды
спектральных классов от F6 до G8, которые
пульсируют в результате нарушения
равновесия между силой тяжести и
внутренним давлением, причем кривая
изменения их параметров напоминает
гармонический закон. С течением времени
колебания ослабевают и затухают; к
настоящему моменту было обнаружено
постепенное прекращение переменности
у звезды RU Жирафа, обнаруженной в 1899
году. К 1966 году ее переменность полностью
прекратилась. Периоды различных цефеид
от 1,5 часов до 45 суток. Все цефеиды –
гиганты большой светимости, причем
светимость строго зависит от периода
по формуле:

M = – 0,35 – 2,08 lg
T.

Так как, в отличие от вышеприведенной
диаграммы Герцшпрунга – Ресселла (см.
рис. 2) зависимость четкая, то и расстояния
можно определять более точно. Для
долгопериодичных цефеид (периоды
колебаний от 1 до 146 суток), относящихся
к звездному населению I
типа (плоской составляющей Галактики),
установлена важная зависимость период
– светимость, согласно которой, чем
короче период колебаний блеска, тем
цефеида слабее по абсолютной величине.
Зная из наблюдений период T,
можно найди абсолютную звездную величину
M, а, зная абсолютную звездную
величину и найдя из наблюдений видимую
звездную величину m, можно найти
расстояние. Такой метод нахождения
расстояний применяется не только для
определения расстояния до самих цефеид,
но и для определения расстояний до
далеких галактик, в составе которых
удалось обнаружить цефеиды (это сделать
не очень трудно, так как цефеиды обладают
достаточно большой светимостью).

Список литературы.

1. Сюняев
   Р. А. Физика космоса, 2-е изд. Москва, изд.
   «Советская энциклопедия», 1986 г.

2. Волынский
   Б. А. Астрономия. Москва, изд. «Просвещение»,
   1971 г.

3. Агекян
   Т. А. Звезды, галактики, Метагалактика.
   Москва, изд. «Наука», 1970 г.

4. Мухин
   Л. М. Мир астрономии. Москва, изд. «Молодая
   гвардия», 1987 г.

5. Левитт
   И. За пределами известного мира: от
   белых карликов до квазаров. Москва,
   изд. «Мир», 1978 г.