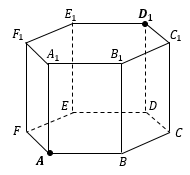
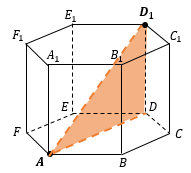
Как найти расстояние отрезка в треугольнике

Как найти расстояние между двумя точками?

Расстоянием между точками также называют прямую,
у которой одна из точек это начало, а соответственно
другая конец. Найти расстояние между этими
двумя точками, значит найти длину прямой,
связывающей точки.

Есть много разных способов найти расстояние между
двумя точками, но самый универсальный, на мой взгляд,
это найти расстояние взяв за основу Теорему Пифагора.
Исходя из этой теоремы, можно сказать, что в нашем
случае расстоянием(прямой), является гипотенуза,
а чем тогда являются точки, сейчас разберемся.

Формулировка великой Теоремы Пифагора звучит так:
в прямоугольном треугольнике квадрат гипотенузы равен
сумме квадратов катетов. Или же кратко, формулой:
( c^2 = a^2 + b^2 ) где c — это гипотенуза, a и b — катеты.

Формулировка этой теоремы применяется почти всегда и везде,
где нужно найти расстояние от чего-то до чего-то. Сейчас, мы
используя эту теорему найдем расстояние между точками.

Итак, для примера возьмем точки с координатами
первой точки — x1 = 0; y1 = 4, второй точки — x2 =3; y2 = 0.
Как же нам теперь выразить точки через катеты a и b ?
Читайте дальше, все гениальное просто.

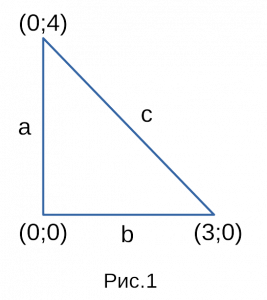
На рисунке 1 мы изобразили для наглядности
прямоугольный треугольник, с координатами
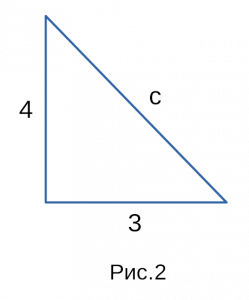
которые мы взяли для примера. На рисунке 2
тот же самый прямоугольный треугольник,
только без координат! Эти два прямоугольных
треугольника идентичные, поэтому вернемся
к Теореме Пифагора.

Заменяем длины катетов a и b, из Теоремы Пифагора,
на разность координат точек. ​Взгляните на формулу,
которая получилась:

Подставляем наши координаты:

В итоге получилось, что расстояние в нашем примере
равно 5(корень из 25). Как видите все просто, и вы можете
смело применять эту формулу, решая не только задачи,
но и на практике, находя расстояние зная только две точки.

Расстояние от точки до прямой

Что называется расстоянием от точки до прямой? Как найти расстояние от точки до прямой?

Расстоянием от точки до прямой называется длина перпендикуляра, опущенного из данной точки на прямую.

Таким образом, чтобы найти расстояние от точки до прямой, надо из точки к прямой провести перпендикуляр и найти его длину.

Например, на рисунке 1 расстояние от точки A до прямой a равно длине перпендикуляра AB, опущенного из точки A на прямую a.

Задачи на нахождение расстояния от точки до прямой сводятся к рассмотрению прямоугольного треугольника.

№ 1. Из точки к прямой проведены две наклонные, длины которых относятся как 2:3, а длины их проекций соответственно равны 2 см и 7 см. Найти расстояние от точки до прямой.

Дано: A∉a,

BC и BD — их проекции, BC=2 см, BD=7 см

1) Пусть k — коэффициент пропорциональности. Тогда AC=2k см, AD=3k см.

2) Рассмотрим треугольник ABC — прямоугольный (так как AB — перпендикуляр к прямой a по условию). По теореме Пифагора

3) Аналогично, из треугольника ABD

4) Приравниваем правые части полученных равенств и находим k:

5) Зная k, найдем AB:

№ 2. Из точки к прямой проведены две наклонные, длины которых равны 13 см и 15 см. Найти расстояние от точки до прямой, если разность проекций наклонных равна 4 см.

Дано: A∉a,

AC и AD — наклонные, AC=13 см, AD=15 см,

BC и BD — их проекции, BD-BC=4 см

1) Пусть BC=x см, тогда BD=x+4 см.

2) Рассмотрим треугольник ABC — прямоугольный (так как AB — перпендикуляр к прямой a по условию). По теореме Пифагора

3) Аналогично, из треугольника ABD

4) Приравниваем правые части полученных равенств и находим x:

5) Зная x, найдем AB:

№ 3. Найти расстояние от точки A до прямой a, если известно, что наклонная AF, длина которой равна c, образует с прямой a угол α.

Дано: A∉a,

Треугольник ABF — прямоугольный (так как AB — перпендикуляр к прямой a по условию). AB — катет, противолежащий углу ACB, AF — гипотенуза.

Все формулы для треугольника

1. Как найти неизвестную сторону треугольника

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c – стороны произвольного треугольника

α , β , γ – противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), ( a):

2. Как узнать сторону прямоугольного треугольника

Есть следующие формулы для определения катета или гипотенузы

a , b – катеты

c – гипотенуза

α , β – острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

Формулы сторон по теореме Пифагора, ( a , b ):

3. Формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

b – сторона (основание)

a – равные стороны

α – углы при основании

β – угол образованный равными сторонами

Формулы длины стороны (основания), (b ):

Формулы длины равных сторон , (a):

4. Найти длину высоты треугольника

Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.

H – высота треугольника

a – сторона, основание

b, c – стороны

β , γ – углы при основании

p – полупериметр, p=(a+b+c)/2

R – радиус описанной окружности

S – площадь треугольника

Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):

[spoiler title=”источники:”]

http://www-formula.ru/2011-10-09-11-08-41

[/spoiler]

Как найти длину отрезка треугольника

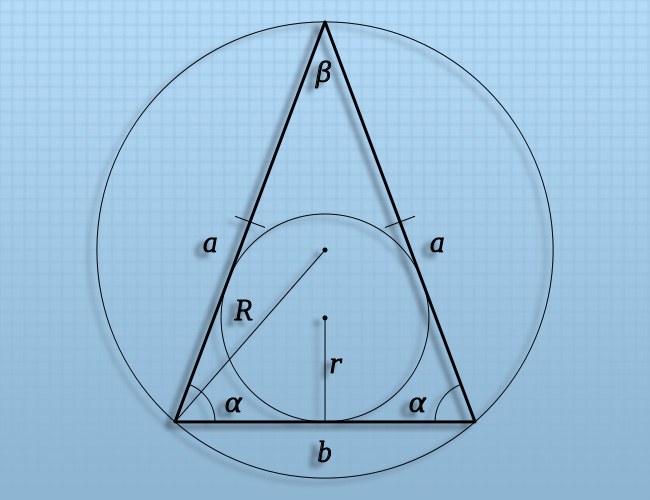
В произвольном треугольнике можно выделить несколько отрезков, длины которых приходится вычислять наиболее часто. Эти отрезки соединяют точки, лежащие в вершинах треугольника, в серединах его сторон, в центрах вписанной и описанной окружностей, а также другие значимые для геометрии треугольника точки. Некоторые варианты расчета длин таких отрезков в евклидовой геометрии приведены ниже.

Инструкция

Если отрезок, который требуется найти, соединяет любые две вершины произвольного треугольника, то он является одной из сторон этой геометрической фигуры. Если известны, например, длины двух других сторон (А и B) и величина угла, который они образуют (γ), то длину этого отрезка (С) вы можете рассчитать, исходя из теоремы косинусов. Сложите квадраты длин сторон, отнимите от результата две длины этих же сторон, умноженных на косинус известного угла, а затем найдите квадратный корень из полученного значения: C=√(А²+B²-2*А*B*cos(γ)).

Если отрезок начинается в одной из вершин треугольника, заканчивается на противолежащей стороне и перпендикулярен ей, то такой отрезок называется высотой (h). Найти его можно, например, зная площадь (S) и длину (A) той стороны, на которую опущена высота – разделите удвоенную площадь на длину стороны: h=2*S/A.

Если отрезок соединяет середину любой стороны произвольного треугольника и вершину, лежащую напротив этой стороны, то называется этот отрезок медианой (m). Найти его длину можно, например, зная длины всех сторон (A, B, C) – сложите удвоенные квадраты длин двух сторон, отнимите от полученного значения квадрат той стороны, на середине которой заканчивается отрезок, а затем найдите квадратный корень из четверти полученного результата: m=√((2*А²+2*B²-C²)/4).

Если отрезок соединяет центр вписанной в произвольный треугольник окружности и любую из точек касания этой окружности со сторонами треугольника, то найти его длину можно, вычислив радиус (r) вписанной окружности. Для этого, например, разделите площадь (S) треугольника на его периметр (P): r=S/P.

Если отрезок соединяет центр окружности, описанной около произвольного треугольника, с любой из вершин этой фигуры, то его длину можно рассчитать, найдя радиус описанной окружности (R). Если известны, например, длина одной из сторон (A) в таком треугольнике и угол (α), лежащий напротив нее, то для вычисления длины нужного вам отрезка разделите длину стороны на удвоенный синус угла: R=A/(2*sin(α)).

Видео по теме

Расстояния

Задача на нахождения расстояния в стереометрической фигуре является главной и самой важной из всех. Прежде всего определимся с тем, что имеется ввиду под словом «расстояние», ведь их может быть бесконечно много.

Расстояние между объектами в геометрии – это кратчайшее из расстояний между ними.

Обозначение:

В стереометрии найти расстояние можно между следующими комбинациями фигур:

РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ

Расстояние между точками– это длина отрезка, соединяющего эти точки.

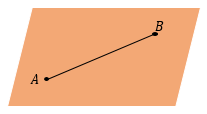
В задачах на стереометрию мы не можем просто воспользоваться линейкой, и длину этого отрезка должны найти аналитически. Поэтому длину отрезка AB между точками A и B находят как сторону треугольника, если отрезок AB удается включить в некоторый треугольник в качестве одной из его сторон.

То есть если в задаче предлагается найти расстояние между точками, нужно задать себе вопрос: «В каком треугольнике этот отрезок является стороной?», затем построить этот треугольник и найти в нем нужную сторону.

Например:

РАССТОЯНИЕ МЕЖДУ ТОЧКОЙ И ПРЯМОЙ

Расстояние от точки до прямой – длина перпендикуляра, опущенного из точки на прямую.

Этот отрезок перпендикуляра можно вычислить, включив его в треугольник (или трапецию) в качестве одной из высот. То есть нужно задать себе вопрос: «В каком треугольнике этот отрезок является высотой?», затем построить этот треугольник и найти в нем высоту.

Например:

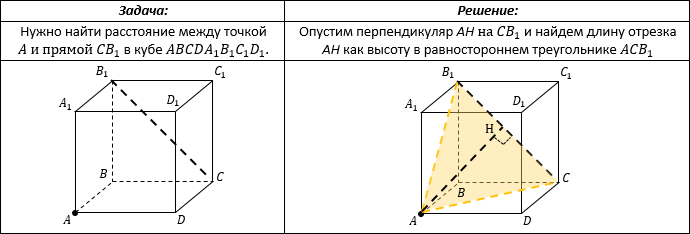
РАССТОЯНИЕ МЕЖДУ ТОЧКОЙ И ПЛОСКОСТЬЮ

Существует несколько способов нахождения расстояния от точки до плоскости:

• Построение перпендикуляра из точки на плоскость.

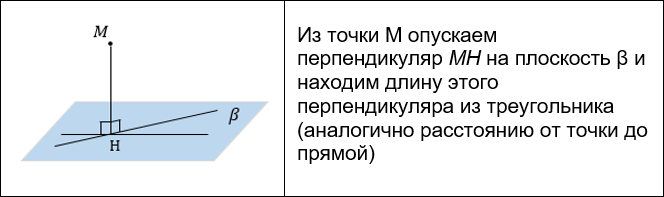
• К этому способу обращаются, если расстояние из точки M на плоскость опускать неудобно, а удобно опустить равный ему перпендикуляр из другой точки, лежащей на одной линии с M.
• Построение перпендикуляра из точки прямой к плоскости.

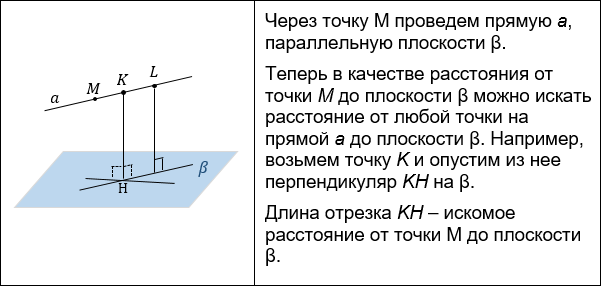
• Построение перпендикуляра из точки плоскости на плоскость.

К этому способу, аналогично, обращаются, если расстояние из точки M на плоскость опускать неудобно, а удобно опустить равный ему перпендикуляр из другой точки, лежащей на одной плоскости с M.

• Через двойное выражение объема.

Расстояние от точки M до плоскости β – это перпендикуляр, опущенный из точки на плоскость, то есть по сути это высота в некоторой пирамиде с вершиной M и плоскостью основания, лежащей на β. Если легко вычислить объем этой пирамиды, используя другое основание и другую высоту, то через этот объем можно найти нужное расстояние.

Например:

РАССТОЯНИЕ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ

Существует несколько способов нахождения расстояния между скрещивающимися прямыми:

1. Построение взаимного перпендикуляра.

2. Построение параллельной прямой.

К этому способу обращаются, если строить взаимный перпендикуляр неудобно и одна из скрещивающихся прямых уже заключена в удобную плоскость.

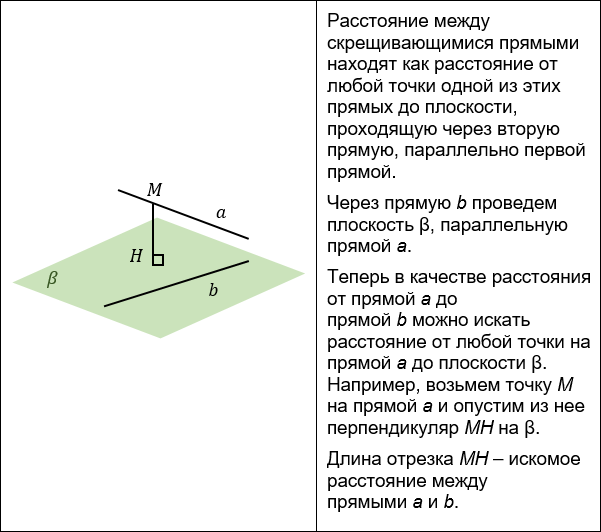К этому способу обращаются, если строить взаимный перпендикуляр неудобно и скрещивающиеся прямые уже заключены в удобные плоскости.

3. Построение параллельной плоскости.

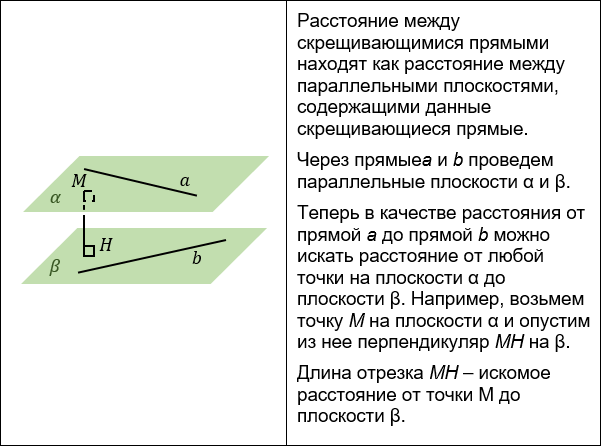
Решать можно, как минимум двумя способами, но в обоих случаях знание теоремы Пифагора, умение её применять в решении, ну, и элементарная внимательность, как показывает практика, просто таки необходимы.

Добавим к чертежу ещё пару отрезков, соединяющих точку М и концы отрезка ВС ( в принципе, для решения достаточно одного из них ):

Так как по условию отрезок АМ перпендикулярен плоскости треугольника ∆ABC, то отрезок АМ будет так же перпендикулярен и отрезку АВ, а значит в прямоугольном треугольнике ∆ВАМ по той самой теореме Пифагора

ВМ² = АВ² + АМ²

С другой стороны, в прямоугольном же треугольнике ∆ВНМ по той же теореме Пифагора

МН² = ВМ² – ВН² подставим в эту формулу выше найденное значение ВМ

МН² = АВ² + АМ² – ВН² ну, а теперь можно подставить и цифровые значения длин отрезков ( учитываем, что ВН = ВС/2 )

МН² = 20² + 24² – 12²

МН² = 400 + 576 – 144 = 832

МН = √832 = 8√13 что и будет ответом на данную задачу.

---

Во втором варианте решения строить дополнительные отрезки ВМ и СМ не нужно:

треугольник ∆AHB прямоугольный и по теореме Пифагора

АН² = АВ² – ВН²

Треугольник ∆МАН так же прямоугольный и по всё той же выше названной теореме Пифагора

МН² = АН² + АМ² подставляем в эту формулу найденное выше значение длина отрезка АН

МН² = АВ² – ВН² + АМ² а теперь подставляем и числовые значения длин отрезков

МН² = 20² – 12² + 24²

МН² = 400 – 144 + 576 = 832

МН = √832

МН = 8√13

Ответ: расстояние от точки М до прямой ВС равно 8√13 см.

Что называется расстоянием от точки до прямой? Как найти расстояние от точки до прямой?

Определение.

Расстоянием от точки до прямой называется длина перпендикуляра, опущенного из данной точки на прямую.

Таким образом, чтобы найти расстояние от точки до прямой, надо из точки к прямой провести перпендикуляр и найти его длину.

Например, на рисунке 1 расстояние от точки A до прямой a равно длине перпендикуляра AB, опущенного из точки A на прямую a.

Задачи на нахождение расстояния от точки до прямой сводятся к рассмотрению прямоугольного треугольника.

Задачи.

№ 1. Из точки к прямой проведены две наклонные, длины которых относятся как 2:3, а длины их проекций соответственно равны 2 см и 7 см. Найти расстояние от точки до прямой.

Дано: A∉a,

   

AC и AD — наклонные, AC:AD=2:3,

BC и BD — их проекции, BC=2 см, BD=7 см

Найти: AB.

Решение:

1) Пусть k — коэффициент пропорциональности. Тогда AC=2k см, AD=3k см.

2) Рассмотрим треугольник ABC — прямоугольный (так как AB — перпендикуляр к прямой a по условию). По теореме Пифагора

   

откуда

   

   

   

3) Аналогично, из треугольника ABD

   

   

   

4) Приравниваем правые части полученных равенств и находим k:

   

   

   

   

5) Зная k, найдем AB:

   

   

Ответ: 4√2 см.

№ 2. Из точки к прямой проведены две наклонные, длины которых равны 13 см и 15 см. Найти расстояние от точки до прямой, если разность проекций наклонных равна 4 см.

Дано: A∉a,

   

AC и AD — наклонные, AC=13 см, AD=15 см,

BC и BD — их проекции, BD-BC=4 см

Найти: AB.

Решение:

1) Пусть BC=x см, тогда BD=x+4 см.

2) Рассмотрим треугольник ABC — прямоугольный (так как AB — перпендикуляр к прямой a по условию). По теореме Пифагора

   

откуда

   

   

3) Аналогично, из треугольника ABD

   

   

4) Приравниваем правые части полученных равенств и находим x:

   

   

   

   

5) Зная x, найдем AB:

   

   

Ответ: 12 см.

№ 3. Найти расстояние от точки A до прямой a, если известно, что наклонная AF, длина которой равна c, образует с прямой a угол α.

Дано: A∉a,

   

AF — наклонная,

AF=c, ∠AFB=α.

Найти: AB.

Решение:

Треугольник ABF — прямоугольный (так как AB — перпендикуляр к прямой a по условию). AB — катет, противолежащий углу ACB, AF — гипотенуза.

По определению синуса

   

   

Ответ: c∙sinα.