Как найти расстояние по координатам вершины

Как найти расстояние по координатам вершины

На этой странице находится все необходимое, чтобы найти расстояние между двумя точками. Просто введите координаты точек и получите ответ и подробное решение с помощью наших онлайн-калькуляторов. Кроме того на сайте можно найти координаты середины отрезка.

Расстояние между двумя точками – это длина отрезка, соединяющего эти точки.

Формула расстояния между двумя точками на плоскости:

d=sqrt{{(x_b – x_a)}^2 + {(y_b – y_a)^2}}

xa и ya – координаты первой точки A,

xb и yb – координаты второй точки B

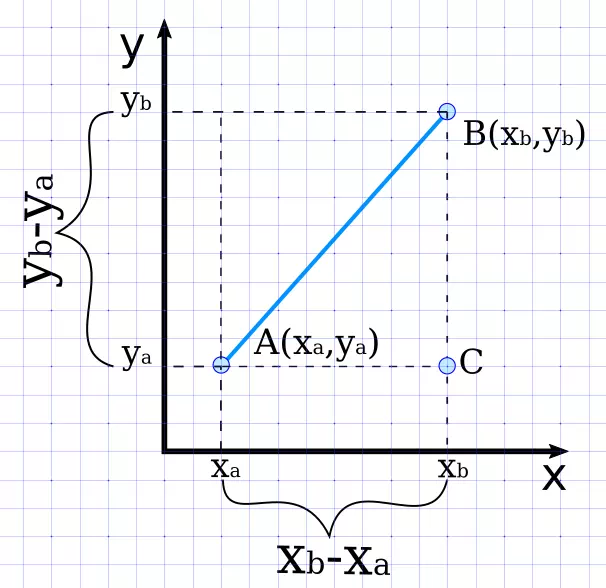
Нахождение расстояния между двумя точками на плоскости сводится к решению треугольника, а точнее – нахождению его гипотенузы. Для этого используется теорема Пифагора. Посмотрите на рисунок.

Вывод формулы расстояния между двумя точками

Соединив отрезком точки A и B, а также опустив перпендикуляры на оси мы получим треугольник ABC. В этом треугольнике стороны AC и BC являются катетами прямоугольного треугольника, а AB – его гипотенузой. Длины катетов AC и BC найти довольно просто:

AC = xb – xa

BC = yb – ya

Осталось применить теорему Пифагора и получить сторону AB, которая является гипотенузой прямоугольного треугольника и расстоянием между точками A и B:

AB=sqrt{{AC}^2 + {BC^2}}

Подставив вместо отрезков AC и BC их длины, получим итоговую формулу расстояния между двумя точками:

AB=sqrt{{(x_b – x_a)}^2 + {(y_b – y_a)^2}} или d=sqrt{{(x_b – x_a)}^2 + {(y_b – y_a)^2}}

Формула расстояния между двумя точками в пространстве:

{d=sqrt{{(x_b – x_a)}^2 + {(y_b – y_a)^2} + {(z_b – z_a)^2}}}

xa, ya и za – координаты первой точки A,

xb, yb и zb – координаты второй точки B

Примеры задач на вычисление середины отрезка

Задача 1

Найдите расстояние между точками А и В, если А(2; 7), В(-2; 7).

Решение

Подставим координаты точек в формулу расстояния между двумя точками на плоскости и вычислим результат:

d=sqrt{{(x_b – x_a)}^2 + {(y_b – y_a)^2}} = sqrt{{(-2 – 2)}^2 + {(7 – 7)^2}} = sqrt{{-4}^2 + {0^2}} = sqrt{16 + 0} = sqrt{16} = 4

Мы получили расстояние между точками и оно равно 4.

Ответ: 4.

Проверим результат с помощью калькулятора .

Источник

Расчет расстояний между точками по их координатам на плоскости элементарен, на поверхности Земли — немного посложнее: мы рассмотрим измерение расстояния и начального азимута между точками без проекционных преобразований.

Для начала разберемся в терминологии.

Введение

Длина дуги большого круга – кратчайшее расстояние между любыми двумя точками находящимися на поверхности сферы, измеренное вдоль линии соединяющей эти две точки (такая линия носит название ортодромии) и проходящей по поверхности сферы или другой поверхности вращения.

Сферическая геометрия отличается от обычной Эвклидовой и уравнения расстояния также принимают другую форму. В Эвклидовой геометрии, кратчайшее расстояние между двумя точками – прямая линия. На сфере, прямых линий не бывает. Эти линии на сфере являются частью больших кругов – окружностей, центры которых совпадают с центром сферы.

Начальный азимут — азимут, взяв который при начале движения из точки А, следуя по большому кругу на кратчайшее расстояние до точки B, конечной точкой будет точка B. При движении из точки A в точку B по линии большого круга азимут из текущего положения на конечную точку B постоянно меняется. Начальный азимут отличен от постоянного, следуя которому, азимут из текущей точки на конечную не меняется, но маршрут следования не является кратчайшим расстоянием между двумя точками.

Через любые две точки на поверхности сферы, если они не прямо противоположны друг другу (то есть не являются антиподами), можно провести уникальный большой круг. Две точки, разделяют большой круг на две дуги. Длина короткой дуги – кратчайшее расстояние между двумя точками. Между двумя точками-антиподами можно провести бесконечное количество больших кругов, но расстояние между ними будет одинаково на любом круге и равно половине окружности круга, или π*R, где R – радиус сферы.

На плоскости (в прямоугольной системе координат), большие круги и их фрагменты, как было упомянуто выше, представляют собой дуги во всех проекциях, кроме гномонической, где большие круги — прямые линии. На практике это означает, что самолеты и другой авиатранспорт всегда использует маршрут минимального расстояния между точками для экономии топлива, то есть полет осуществляется по расстоянию большого круга, на плоскости это выглядит как дуга.

Форма Земли может быть описана как сфера, поэтому уравнения для вычисления расстояний на большом круге важны для вычисления кратчайшего расстояния между точками на поверхности Земли и часто используются в навигации.

Вычисление расстояния этим методом более эффективно и во многих случаях более точно, чем вычисление его для спроектированных координат (в прямоугольных системах координат), поскольку, во-первых, для этого не надо переводить географические координаты в прямоугольную систему координат (осуществлять проекционные преобразования) и, во-вторых, многие проекции, если неправильно выбраны, могу привести к значительным искажениям длин в силу особенностей проекционных искажений.

Известно, что более точно описывает форму Земли не сфера, а эллипсоид, однако в данной статье рассматривается вычисление расстояний именно на сфере, для вычислений используется сфера радиусом 6372795 метров, что может привести к ошибке вычисления расстояний порядка 0.5%.

Формулы

Существует три способа расчета сферического расстояния большого круга.

1. Сферическая теорема косинусов

В случае маленьких расстояний и небольшой разрядности вычисления (количество знаков после запятой), использование формулы может приводить к значительным ошибкам связанным с округлением.

φ1, λ1; φ2, λ2 — широта и долгота двух точек в радианах

Δλ — разница координат по долготе

Δδ — угловая разница

Δδ = arccos {sin φ1 sin φ2 + cos φ1 cos φ2 cos Δλ}

Для перевода углового расстояния в метрическое, нужно угловую разницу умножить на радиус Земли (6372795 метров), единицы конечного расстояния будут равны единицам, в которых выражен радиус (в данном случае — метры).

2. Формула гаверсинусов

Используется, чтобы избежать проблем с небольшими расстояниями.

3. Модификация для антиподов

Предыдущая формула также подвержена проблеме точек-антиподов, чтобы ее решить используется следующая ее модификация.

Моя реализация на РНР

// Радиус земли
define('EARTH_RADIUS', 6372795);
 
/*
* Расстояние между двумя точками
* $φA, $λA - широта, долгота 1-й точки,
* $φB, $λB - широта, долгота 2-й точки
* Написано по мотивам http://gis-lab.info/qa/great-circles.html
* Михаил Кобзарев <mikhail@kobzarev.com>
*
*/
function calculateTheDistance ($φA, $λA, $φB, $λB) {
 
// перевести координаты в радианы
$lat1 = $φA * M_PI / 180;
$lat2 = $φB * M_PI / 180;
$long1 = $λA * M_PI / 180;
$long2 = $λB * M_PI / 180;
 
// косинусы и синусы широт и разницы долгот
$cl1 = cos($lat1);
$cl2 = cos($lat2);
$sl1 = sin($lat1);
$sl2 = sin($lat2);
$delta = $long2 - $long1;
$cdelta = cos($delta);
$sdelta = sin($delta);
 
// вычисления длины большого круга
$y = sqrt(pow($cl2 * $sdelta, 2) + pow($cl1 * $sl2 - $sl1 * $cl2 * $cdelta, 2));
$x = $sl1 * $sl2 + $cl1 * $cl2 * $cdelta;
 
//
$ad = atan2($y, $x);
$dist = $ad * EARTH_RADIUS;
 
return $dist;
}

Пример вызова функции:

$lat1 = 77.1539;
$long1 = -139.398;
$lat2 = -77.1804;
$long2 = -139.55;
 
echo calculateTheDistance($lat1, $long1, $lat2, $long2) . " метров";
// Вернет "17166029 метров"

Статья взята с сайта gis-lab.info Автор: Максим Дубинин

Ссылки

  • Вычисление расстояния и начального азимута между двумя точками на сфере(официальный источник)
  • Haversine formula
  • Способы расчета сферического расстояния большого круга
  • Сферическая система координат
  • Сферические координаты
  • Calculate distance, bearing and more between Latitude/Longitude points

coordinates distance PHP tips tricks

Источник

На чтение 5 мин. Просмотров 2.4k. Опубликовано 12.08.2022

Спутниковые координаты не только помогают найти маршрут до нужного места, но и позволяют рассчитать отрезок между двумя любыми точками в пространстве или на данной плоскости. Зная необходимые данные и координаты интересующих объектов, можно найти расстояние в километрах или метрах между этими длинами или отрезками нужной длины. Для этого применяется либо сложная формула для самостоятельного решения, либо онлайн-калькуляторы на сайте или картографические программы, выполняющие работу автоматически.

Содержание

  1. Координаты GPS
  2. Вычисление расстояния между двумя точками через формулу
  3. Формула для нахождения расстояния между точками
  4. Способы решения и нахождения расстояния между точками по координатам
  5. Онлайн-калькулятор для расчета расстояния между точками по координатам
  6. Картографическая программа для нахождения расстояния между точками
  7. Откуда берется погрешность при расчете расстояния между точками

Координаты GPS

Координаты GPS (Global Positioning System) – это цифровые обозначения местоположения устройства в пространстве или на плоскости, указанные в формате соотнесения географических широты и долготы. Данные точки на отрезке определенной длины вычисляются при помощи связи со спутником. Запускается сложная система навигации, которая, помимо указания координат, может определить расстояние между двумя точками в пространстве или на плоскости, проложить маршрут между отрезками длины и рассчитать время перемещения как пешком, так и на разных видах транспорта. В основе работы лежит всемирная система координат WGS 84.

Координаты GPS

Координаты GPS

Чтобы найти местоположение и расстояние между двумя данными точками или отрезками длины в пространстве и на плоскости по координатам GPS, можно пользоваться как специальным навигатором или профессиональным навигационным прибором, так и обычным смартфоном или планшетом.

Вычисление расстояния между двумя точками через формулу

Найти расстояние между двумя точками в пространстве или на плоскости можно как по прямой, так и по маршруту (с учетом расположения дорог, их поворотов, объездов и пр.). В первом случае применима специальная формула, воспользоваться которой можно как в автоматическом режиме, введя известные данные отрезков в калькулятор на сайте, так и самостоятельно, проведя итоговое решение с нужными материалами на бумаге.

Кратчайшим (прямым) расстоянием считается дуга, проходящая по поверхности Земли от точки А в точку Б. Чтобы найти ее длину, применяют так называемую модифицированную формулу гаверсинусов, учитывающую радиус планеты.

Известно, что Земля – не идеальный шар, а несколько приплюснутый, потому и радиус у нее в разных точках различен. Ввиду этого для подсчета кратчайшего расстояния между точками используется усредненное значение радиуса относительно оси (6372.795 км для Земли), что допускает погрешность итогового значения около 0,5 %.

Формула для нахождения расстояния между точками

В формуле, при помощи которой можно найти расстояния между двумя данными точками планеты с использованием координат, присутствуют следующие величины (известные из математики):

  • d – центральный угол (перпендикуляр) между двумя данными точками, лежащими на большом круге (т. е. на окружности, получаемой при сечении центральной части шара плоскостью);
  • r – радиус сферы (т. е. усредненное значение радиуса Земли: 6372.795 км);
  • y₁ и y₂ –  широта двух точек в радианах;
  • x₁ и x₂ – долгота двух точек в радианах.

Получим следующую тригонометрическую формулу, плавно вытекающую из теоремы пифагора (евклидова геометрия), которая равна:

cos(d) = sin(y₁)·sin(y₂) + cos(y₁)·cos(y₂)·cos(x₁ − x₂)

Данное соотношение можно получить из прямоугольного треугольника.

Подставив в формулу заданные значения точек, и получим вычисление.

Для того чтобы найти ответ про расстояние между двумя точками координат в километрах, поможет формула:

L = d·R.

Способы решения и нахождения расстояния между точками по координатам

Чтобы провести решение и получить ответ о расстоянии точек в пространстве или плоскости по координатам GPS, необязательно использовать формулу вручную. Ответ о расстоянии между точками по координатам получим при помощи специальных утилит.

Онлайн-калькулятор для расчета расстояния между точками по координатам

В интернете есть множество сайтов с однотипными формулами в онлайн-калькуляторах для решения и нахождения прямого расстояния между двумя точками по координатам. Для этого нужно узнать широту и долготу двух искомых точек в пространстве или на плоскости и вбить эти данные в соответствующие окошки формулы (чем больше знаков после запятой у каждой точки известно, тем точнее получим значение).

Картографическая программа для нахождения расстояния между точками

Вычислять расстояние между двумя точками на плоскости по координатам и давать точный ответ умеет любое приложение-навигатор и без вычисления по формуле, например:

  • «Карты»;
  • «Google.Maps»;
  • «Google Планета Земля»;
  • «SAS.Планета».

Определение координат объекта в Google Maps на компьютере

Определение координат объекта в Google Maps на компьютере не по формуле

Для определения расстояния между точками не по дорогам и маршрутам, а напрямую по двум точкам, применяется инструмент «Линейка».

Многие из популярных навигаторов способны определять расстояние по координатам двух точек онлайн без формул: это можно сделать на сайте в разделе «Азимут» или «Другие вычисления».

На заметку. Наиболее точные данные между точками предоставляют материалы и таблицы кадастровых справочников, но также в них много информации, лишней для обычного пользователя.

Откуда берется погрешность при расчете расстояния между точками

При вычислении прямого расстояния между координатами двух точек применяется подсчет длины дуги этих точек, для чего берется радиус точек (его приблизительное среднее значение ввиду особенностей формы Земли). Из-за этого возникает погрешность, т. е. мы получим не точную информацию о расстоянии между точками.

Чем больше искомое расстояние, тем больше получим погрешность в расстоянии между точками.

Также неточность между точками получим тогда, когда при вычислениях расстояния между точками берут недостаточно цифр после запятой в координатах: результат будет приблизительным.

Так, между любыми двумя известными точками на чертеже Земли можно проложить как обычное расстояние по дорогам, так и прямую линию, которая соединяет каждую точку. Вычисления точек проводят вручную или автоматически, причем во втором случае даже будет известна возможная погрешность, которую получим при нахождении расстояние между точками, неизбежная при измерении сферы Земли.

Источник

Как найти расстояние от точки до вершины

Вершина любой плоской или объемной геометрической фигуры однозначно определяется своими координатами в пространстве. Точно так же может быть однозначно определена и любая произвольная точка в той же системе координат, а это дает возможность вычислить расстояние между этой произвольной точкой и вершиной фигуры.

Как найти расстояние от точки до вершины

Вам понадобится

  • – бумага;
  • – ручка или карандаш;
  • – калькулятор.

Инструкция

Сведите задачу к нахождению длины отрезка между двумя точками, если координаты заданной в условиях задачи точки и вершины геометрической фигуры известны. Эту длину можно вычислить, воспользовавшись теоремой Пифагора применительно к проекциям отрезка на оси координат – она будет равна квадратному корню из суммы квадратов длин всех проекций. Например, пусть в трехмерной системе координат заданы точка A(X₁;Y₁;Z₁) и вершина C объемной фигуры любой геометрической формы с координатами (X₂;Y₂;Z₂). Тогда длины проекций отрезка между ними на координатные оси можно определить как X₁-X₂, Y₁-Y₂ и Z₁-Z₂, а длину самого отрезка – как √((X₁-X₂)²+(Y₁-Y₂)²+(Z₁-Z₂)²). Например, если координаты точки A(5;9;1), а вершины C(7;8;10), то расстояние между ними будет равно √((5-7)²+(9-8)²+(1-10)²) = √(-2²+1²+(-9)²) = √(4+1+81) = √86 ≈ 9,274.

Вычислите сначала координаты вершины, если в явном виде в условиях задачи они не представлены. Конкретный способ расчета зависит от типа фигуры и известных дополнительных параметров. Например, если известны трехмерные координаты трех вершин параллелограмма A(X₁;Y₁;Z₁), B(X₂;Y₂;Z₂) и C(X₃;Y₃;Z₃), то координаты четвертой его вершины (противоположной вершине B) будут равны (X₃+X₂-X₁; Y₃+Y₂-Y₁; Z₃+Z₂-Z₁). После определения координат недостающей вершины вычисление расстояния между ней и произвольной точкой вновь сведется к определению длины отрезка между двумя этими точками в заданной системе координат – сделайте это тем же способом, который был описан в предыдущем шаге. Например, для вершины описанного в этом шаге параллелограмма и точки E с координатами (X₄;Y₄;Z₄) формулу вычисления расстояния из предыдущего шага можно изменить так: √((X₃+X₂-X₁-X₄)²+(Y₃+Y₂-Y₁-Y₄)²+(Z₃+Z₂-Z₁-Z₄)²).

Для практических расчетов можно использовать, например, встроенный в поисковую систему Google калькулятор. Так, чтобы вычислить значение по формуле, полученной на предыдущем шаге, для точек с координатами A(7;5;2), B(4;11;3), C(15;2;0), E(7;9;2), введите такой поисковый запрос: sqrt((15+4-7-7)^2+(2+11-5-9)^2+(0+3-2-2)^2). Поисковик рассчитает и отобразит результат вычислений (5,19615242).

Видео по теме

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Задача простая. Нужно вычислить расстояние между двумя точками на карте, при этом известны только их географические координаты, то есть широта и долгота. Для примера вычислим расстояние между Москвой и Питером, но данная методика, конечно же, будет применима и к другим двум точкам местности. В наше время у многих людей есть такие компасы, например при смартфонах, которые показывают не только направление, но и географические координаты.

Итак, задача: вычислить расстояние между двумя городами. Известно только одно – географические координаты, то есть широта и долгота. Посмотрим эти данные в справочнике, ну или в Википедии.

Итак, что нам известно: координаты Москвы:

55,7522 град. с.ш., 37.6156 град. в.д.

Координаты Петербурга:

59,89444 град. с.ш., 30,26417 град. в.д.

Построим с помощью Excel трапецию:

Рисунок 1.
Рисунок 1.

Итак, у нас есть трапеция ABCD. На ней точка D – это Москва, точка B – это Петербург. Отрезок AB проходит по меридиану Петербурга, BC – по параллели Петербурга, CD – по меридиану Москвы и AD – по параллели Москвы.

Что нам известно? Во-первых известны все географические координаты каждой из точек:

A: 55,7522, 30,26417;

B: 59,89444, 30,26417;

C: 59,89444, 37,6156;

D: 55,7522, 37,6156.

Вычислить AB и CD достаточно просто. На меридианах в градусе примерно одинаковое число километров. Это расстояние можно взять из справочных данных, и оно составляет примерно 111,1 км в каждом градусе.

Нужная нам разница в градусах – это 59,89444-55,7522, или 4,14224. А это значит, что разница в километрах – это 4,14224*111,1=460,2029 км.

Что же касается оснований трапеции, там тоже все достаточно просто. Экватор – это ноль градусов северной широты, и длина каждого градуса на экваторе около 111,3 км. Поскольку косинус ноля – это единица, то для любой параллели верна следующая формула: длина каждого градуса равна произведению 111,3 на косинус того угла, который числится в градусах северной широты (ну или южной, если это происходит южнее экватора).

Итак, с помощью Excel вычислим нужные нам косинусы:

  • cos(55.7522) = 0,562773
  • cos(59.89444) = 0,501595

Это значит, что 1 градус в верхнем основании нашей трапеции =111,3*0,501595=55,82749 км, а один градус в нижнем основании трапеции =111,3*0,562773=62,6366 км. Поскольку число градусов одинаково как в верхнем, так и в нижнем основаниях трапеции и составляет 37,6156-30,26417, то есть 7,35143 градуса. Но число километров в верхнем и нижнем основаниях трапеции не одинаковое.

Рассчитаем эти расстояния в километрах. BC=7,35143*55,82749=410,4119 км.

AD=7,35143*62,6366=460,469 км.

Теперь проведем высоту BH в нашей трапеции:

Рисунок 2.
Рисунок 2.

В прямоугольном треугольнике ABH нам известно, что гипотенуза равна 460,2029 км, малый катет тоже известен (это половина разницы между длинами оснований трапеции, то есть 0,5*[460,469-410,4119], то есть 0,5*50,05711, или 25,02856 км).

Итак, найдем высоту трапеции ABCD, ее можно вычислить с помощью теоремы Пифагора. Напомню, что мы знаем и длину гипотенузы, и длину наименьшего из катетов.

  • Квадрат гипотенузы: 211786,7
  • Квадрат известного катета: 626,4
  • Разность между этими числами: 211160,2

Корень из этой разности – 459,5218 км. Это и есть наша высота трапеции, то есть BH.

Задача почти решена. Для нахождения расстояния между Москвой и Питером нам нужно вычислить диагональ трапеции, то есть BD. Нарисуем эту линию:

Рисунок 3.
Рисунок 3.

Итак, у нас есть треугольник BHD. BH мы только что вычислили (459,5218 км), HD тоже известно (нужно от большего основания трапеции отнять AH. 460,469-25,02856=435,4404).

Два катета известны, нужно найти гипотенузу. По той же теореме Пифагора, и мы увидим, что гипотенуза будет равна 633,0629 км. Это и есть расстояние от Питера до Москвы.

Проверим наши вычисления, спросив у Яндекса, сколько составляет расстояние от Питера до Москвы.

Рисунок 4.
Рисунок 4.

Мы увидим ответ – 634 км. При вычислениях по нашей методике получилось чуть больше, чем 633 км. Это значит, что погрешность при данном виде вычислений достаточна мала. Но если учесть, что крупные города – это не маленькие точки, а большие расстояния с севера на юг и с запада на восток, то можно сказать, что мы вычислили все правильно.

А на этом пока всё, подписывайтесь на мой канал и до новых встреч!

Источник

Добавить комментарий