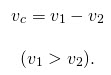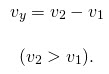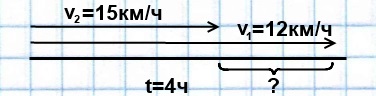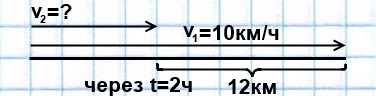Памятка
по математике 4 класс по теме
«Скорость, время, расстояние»
S – расстояние ( путь); измеряется в км, м и т.д.
V – скорость ( это расстояние, преодолеваемое за единицу времени); измеряется в км/ч, м/ мин и т.д.
t- время; измеряется в часах, минутах и т.д.
- Чтобы найти расстояние, нужно скорость умножить на время. S =V х t
- Чтобы найти скорость, нужно расстояние разделить на время.
V = S : t
- Чтобы найти время, нужно расстояние разделить на скорость.
t = S :V
Задача на нахождение расстояния
Пешеход шёл со скоростью 5 километров в час. Какой путь он пройдёт за 3 часа?
5 х 3 = 15 ( км)
Ответ: 15 километров пройдёт пешеход.
Задача на нахождение скорости
Пешеход за 3 часа прошёл 15 километров. С какой скоростью шёл пешеход?
15 : 3 = 5 ( км/ч)
Ответ: 5 км/ ч скорость пешехода.
Задача на нахождение времени
Пешеход шёл со скоростью 5 километров в час и прошёл 15 километров. Сколько времени шёл пешеход?
15 : 5 = 3 ( ч)
Ответ: 3 часа шёл пешеход.
Математика, 4 класс
Урок № 36. Связь между скоростью, временем и расстоянием
Перечень вопросов, рассматриваемых в теме:
– как скорость взаимосвязана с величинами время, расстояние?
– как определить скорость по известному расстоянию и времени движения?
– как определить расстояние по известной скорости и времени движения?
– как определить время движения по известному расстоянию и скорости?
Глоссарий по теме:
Скорость — это расстояние, пройденное за единицу времени.
Скорость, расстояние и время можно измерять и сравнивать, значит это величины.
Чтобы узнать скорость движения, нужно расстояние разделить на время.
Чтобы узнать расстояние, нужно скорость умножить на время.
Чтобы найти время, нужно расстояние разделить на скорость.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 4 класс. Учебник для общеобразовательных организаций. Ч.2 – М.; Просвещение, 2017. – с.6-8.
2. Моро М. И., Волкова С. И. Математика. Рабочая тетрадь 4 класс. Часть 2. М.; Просвещение, 2016. – с.15.
3. Волкова С. И. Математика. Проверочные работы 4 класс. М.; Просвещение, 2017. – с.54.
Теоретический материал для самостоятельного изучения
В таблицах даны скорости вороны и комара, льва и кенгуру. Определи, какое расстояние пролетит ворона за 2 мин, а комар за 3 с. Какой путь преодолеет лев за 4 ч, а кенгуру за 30 мин?
Мотоциклист едет со скоростью 41 км/ч. Какое расстояние он преодолеет за 5 ч, если будет двигаться с той же скоростью?
Для того чтобы узнать расстояние, необходимо скорость, 41 км в час умножить на время, 5 часов. Таким образом, расстояние, которое преодолел мотоциклист равно 205 км.
41 · 5 = 205 км
Чтобы найти расстояние, нужно скорость умножить на время.
Будем учиться записывать задачи в таблицу и решать их.
Задача 1.
Черепаха двигалась со скоростью 5 м/ мин. Какое расстояние прошла она за 3 минуты?
Задача 2.
Слон двигался со скоростью 100 м/мин. Какое расстояние он прошёл за 10 мин?
Составим таблицу и рассмотрим, как можно найти расстояние, зная скорость и время движения.
Составим таблицу и рассмотрим, как можно найти расстояние, зная скорость и время движения. Расстояние, которое прошли черепаха и расстояние, которое прошёл слон, нам неизвестны. Поставим в таблице знаки «вопрос».
5 м/мин – это скорость черепахи, 100 м/мин – это скорость слона. Запишем данные в колонку «Скорость». 3 минуты это время движения черепахи, 10 минут – время, которое находился в пути слон. Запишем эти данные в третью колонку.
|
Скорость |
Время |
Расстояние |
|
|
Черепаха |
5 м/мин |
3 мин |
? |
|
Слон |
100 м/мин |
10 мин |
? |
Мы теперь знаем, чтобы найти расстояние, нужно скорость умножить на время. Запишем решение и ответ.
Скорость 5 м/мин умножим на время 3 мин, получится 15 метров. Это расстояние, которое прошла черепаха.
Скорость 100 м/мин умножим на время 10 мин, получится 1000 метров. Это расстояние, которое прошёл слон.
5 · 3 = 15 (м)
100 · 10 = 1000 (м)
Ответ: черепаха за 3мин прошла 15 м, а слон за 10 мин прошёл 1000 м.
Итак, чтобы найти расстояние, нужно скорость умножить на время.
А теперь рассмотрим задачу на нахождение времени.
Расстояние от города до посёлка 20 км. Из города вышел пешеход со скоростью 5 км/ч. Сколько времени потребуется пешеходу, чтобы пройти весь путь?
Это задача на движение, значит, речь идет о величинах скорость, время, расстояние. Заполним таблицу.
В задаче нужно узнать время движения пешехода. Оно нам неизвестно, поставим знак вопроса. Известно, что расстояние, которое нужно пешеходу равно 20 км.5 км/ч это скорость движения.
|
Скорость |
Время |
Расстояние |
|
5 км/ч |
? |
20 км |
Правило: чтобы найти время, нужно расстояние разделить на скорость. Запишем решение:
20 : 5 = 4 (ч)
Ответ: пешеход будет в пути 4 часа.
Запоминаем правило нахождения времени: чтобы узнать время, расстояние разделить на скорость.
Задания тренировочного модуля:
1. Заполните кроссворд.
Решите кроссворд.
По горизонтали:
2. Плот проплыл 630 м со скоростью 90 м/мин. Чему равно время движения плота?
3. Анника за 6 мин проехала на велосипеде 600 м. Чему равно время движения Анники?
По вертикали:
1. За 7 мин улитка проползла 7 дм. Чему равна скорость движения улитки?
Правильные ответы:
По горизонтали: 2.семь. 3. сто.
По вертикали: 1. десять.
2. Распределите единицы измерения величин по группам. Перенесите данные в соответствующие столбики.
Варианты ответа:
1. 85 см/мин
2. 120 с
3. 548 км
4. 12 мин
5. 850 м/с
6. 600 км/ч
7. 10 ч
8. 2500 м
9. 41 дм
Правильный вариант:
|
Скорость |
Время |
Расстояние |
|
85 см/мин 850 м/с 600 км/ч |
120 с 12 мин 10 ч |
548 км 2500 м 41 дм |
3. Вставьте пропущенное слово, выбирая из списка правильный ответ.
Как пройденный путь зависит от скорости?
Если скорость движения увеличить в несколько раз, то пройденный путь_______ во столько же раз.
Варианты ответа: уменьшится, увеличится.
Правильный вариант: увеличится.
- Главная
- Справочники
- Справочник по математике для начальной школы
- Задачи
- Скорость, время, расстояние
Скорость движения – это расстояние, пройденное за единицу времени.
Единицей времени является 1 секунда, 1 минута или 1 час.
Чтобы определить скорость движения, нужно использовать величины – расстояние и время.
Чтобы найти скорость, нужно расстояние разделить на время.
В качестве единиц измерения скорости мы будем пользоваться единицами длины и единицами времени. Обычно используют такие единицы скорости, как метр в секунду, метр в минуту, километр в час и другие, а записывают так: м/с, м/мин, км/ч. Обратите внимание, что предлог “в” в математике заменили чёрточкой “ / ”.
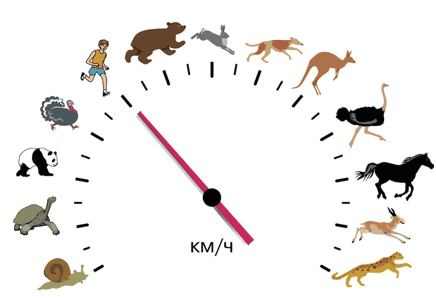
Например, скорость страуса – 7 км/ч.
Скорость черепахи – 5 м/с.
Прибор для измерения скорости: спидометр.
Чем меньше времени затрачено на дорогу, тем больше скорость движения.
Чем меньше скорость движения, тем больше времени требуется на дорогу.
Чтобы найти время, нужно расстояние разделить на скорость.
Чтобы найти расстояние, нужно скорость умножить на время.
При решении задач на движение стоит помнить, что при движении навстречу друг другу скорости складываются, а при движении друг за другом – вычитается.
Складывая две скорости при движении навстречу, мы получаем скорость, с которой пешеходы приближаются друг к другу. Её мы будем называть скоростью сближения.
Складывая две скорость при движении в противоположных направлениях, мы получаем скорость, с которой объекты удаляются друг от друга. Её мы будем называть скоростью удаления.
Место встречи всегда ближе к пункту, из которого вышел пешеход, у которого скорость меньше.
Советуем посмотреть:
Образцы оформления задачи
Обратные задачи
Цена. Количество. Стоимость
Задачи
Правило встречается в следующих упражнениях:
3 класс
Страница 3. Урок 1,
Петерсон, Учебник, часть 3
Страница 5. Урок 2,
Петерсон, Учебник, часть 3
Страница 7. Урок 3,
Петерсон, Учебник, часть 3
Страница 11. Урок 5,
Петерсон, Учебник, часть 3
Страница 19. Урок 8,
Петерсон, Учебник, часть 3
Страница 20. Урок 9,
Петерсон, Учебник, часть 3
Страница 27. Урок 12,
Петерсон, Учебник, часть 3
Страница 29. Урок 13,
Петерсон, Учебник, часть 3
Страница 44. Урок 20,
Петерсон, Учебник, часть 3
Страница 74. Повторение,
Петерсон, Учебник, часть 3
4 класс
Страница 86. Тест 4. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 39,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 51,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 60,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 63,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 76,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 78,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 100,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 3,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 9,
Моро, Волкова, Рабочая тетрадь, часть 2
5 класс
Задание 97,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1394,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1423,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1545,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1709,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1788,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 475,
Мерзляк, Полонский, Якир, Учебник
Номер 1045,
Мерзляк, Полонский, Якир, Учебник
Номер 1120,
Мерзляк, Полонский, Якир, Учебник
Номер 2,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 381,
Мерзляк, Полонский, Якир, Учебник
Номер 454,
Мерзляк, Полонский, Якир, Учебник
Номер 671,
Мерзляк, Полонский, Якир, Учебник
Задание 396,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 481,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 570,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1120,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1350,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1502,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 428,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
7 класс
Номер 16,
Мерзляк, Полонский, Якир, Учебник
Номер 146,
Мерзляк, Полонский, Якир, Учебник
Номер 255,
Мерзляк, Полонский, Якир, Учебник
Номер 525,
Мерзляк, Полонский, Якир, Учебник
Номер 767,
Мерзляк, Полонский, Якир, Учебник
Номер 980,
Мерзляк, Полонский, Якир, Учебник
Номер 1088,
Мерзляк, Полонский, Якир, Учебник
Номер 1094,
Мерзляк, Полонский, Якир, Учебник
Номер 1115,
Мерзляк, Полонский, Якир, Учебник
Номер 1118,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 9,
Мерзляк, Полонский, Якир, Учебник
Номер 91,
Мерзляк, Полонский, Якир, Учебник
Номер 198,
Мерзляк, Полонский, Якир, Учебник
Номер 214,
Мерзляк, Полонский, Якир, Учебник
Номер 215,
Мерзляк, Полонский, Якир, Учебник
Номер 216,
Мерзляк, Полонский, Якир, Учебник
Номер 223,
Мерзляк, Полонский, Якир, Учебник
Номер 267,
Мерзляк, Полонский, Якир, Учебник
Номер 315,
Мерзляк, Полонский, Якир, Учебник
Номер 371,
Мерзляк, Полонский, Якир, Учебник
Существует несколько типов задач на движение. Примеры решения всех типов задач с пояснениями мы рассмотрим в этой статье.
Задачи на движение в одном направлении
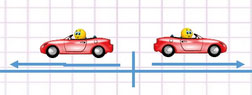
Задачи на движении в одном направлении относятся к одному из трех основных видов задач на движение.
Если два объекта выехали из одного пункта одновременно, то, поскольку они имеют разные скорости, объекты удаляются друг от друга. Чтобы найти скорость удаления, надо из большей скорости вычесть меньшую:
Если из одного пункта выехал один объект, а спустя некоторое время в том же направлении вслед за ним выехал другой объект, то они могут как сближаться, так и удаляться друг от друга.
Если скорость объекта, движущегося впереди, меньше движущегося вслед за ним объекта, то второй догоняет первого и они сближаются.
Чтобы найти скорость сближения, надо из большей скорости вычесть меньшую:
Если скорость объекта, который идет впереди, больше скорости объекта, который движется следом, то второй не сможет догнать первого и они удаляются друг от друга.
Скорость удаления находим аналогично — из большей скорости вычитаем меньшую:
Задачи на скорость сближения
Задача 1
Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?
Решение:
Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалится от города на:
40 · 4 = 160 (км)
Второй автомобиль движется быстрее первого, значит каждый час расстояние между автомобилями будет сокращаться на разность их скоростей:
60 – 40 = 20 (км/ч) – это скорость сближения автомобилей
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся:
160 : 20 = 8 (ч)
Решение задачи по действиям можно записать так:
1) 40 · 4 = 160 (км) – расстояние между автомобилями
2) 60 – 40 = 20 (км/ч) – скорость сближения автомобилей
3) 160 : 20 = 8 (ч)
Ответ: Второй автомобиль догонит первый через 8 часов.
Задача 2
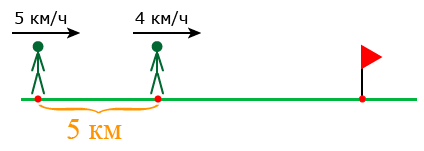
Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Решение:
Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов:
5 – 4 = 1 (км/ч)
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого:
5 : 1 = 5 (ч)
Решение задачи по действиям можно записать так:
1) 5 – 4 = 1 (км/ч) – это скорость сближения пешеходов
2) 5 : 1 = 5 (ч)
Ответ: Через 5 часов второй пешеход догонит первого.
Задача 3
Из одного села в одном направлении одновременно выехали два велосипедиста. Скорость одного из них — 15 км/ч, скорость другого — 12 км/ч. Какое расстояние будет через ними через 4 часа?
Решение:
1) 15-12=3 (км/ч) скорость удаления велосипедистов
2) 3∙4=12 (км) такое расстояние будет между велосипедистами через 4 часа.
Ответ: Через 4 часа расстояние между велосипедистами составит 12 км.
Задача 4
Из села на станцию одновременно вышел пешеход и выехал велосипедист. Через 2 часа велосипедист опережал пешехода на 12 км. Найти скорость пешехода, если скорость велосипедиста 10 км/ч.
Решение:
1) 12:2=6 (км/ч) скорость удаления велосипедиста и пешехода
2) 10-6=4 (км/ч) скорость пешехода.
Ответ: Скорость пешехода составляет 4 км/ч.
Задачи на скорость удаления
Задача 1
Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго – 40 км/ч.
- Чему равна скорость удаления между автомобилями?
- Какое расстояние будет между автомобилями через 3 часа?
- Через сколько часов расстояние между ними будет 200 км?
Решение:
Сначала узнаем скорость удаления автомобилей друг от друга, для этого вычтем из большей скорости меньшую:
80 – 40 = 40 (км/ч)
Каждый час автомобили отдаляются друг от друга на 40 км. Теперь можно узнать сколько километров будет между ними через 3 часа, для этого скорость удаления умножим на 3:
40 · 3 = 120 (км)
Чтобы узнать через сколько часов расстояние между автомобилями станет 200 км, надо расстояние разделить на скорость удаления:
200 : 40 = 5 (ч)
Ответ:
- Скорость удаления между автомобилями равна 40 км/ч.
- Через 3 часа между автомобилями будет 120 км.
- Через 5 часов между автомобилями будет расстояние в 200 км.
Движение навстречу друг другу
Если два объекта движутся навстречу друг другу, то они сближаются. Чтобы найти скорость сближения двух объектов, движущихся навстречу друг другу, надо сложить их скорости:
Скорость сближения больше, чем скорость каждого из них.
Задача 1
Из поселка и города навстречу друг другу, одновременно выехали два автобуса. Один автобус до встречи проехал 100 км со скоростью 25 км/час. Сколько километров до встречи проехал второй автобус, если его скорость 50 км/час.
Решение:
1) 100 : 25 = 4 (часа ехал один автобус)
2) 50 * 4 = 200
Решение в виде выражения: 50 * (100 : 25) = 200
Ответ: второй автобус проехал до встречи 200 км.
Расстояние между двумя пристанями 90 км. От каждой из них одновременно навстречу друг другу вышли два теплохода. Сколько часов им понадобится чтобы встретиться, если скорость первого 20 км/час, а второго 25 км/час?
Решение:
1) 25 + 20 = 45 (сумма скоростей теплоходов)
2) 90 : 45 = 2
Решение в виде выражения:90 : (20 + 25) = 2
Ответ: Теплоходы встретятся через 2 часа.
Задача 3
От двух станций, расстояние между которыми 564 км., одновременно навстречу друг другу вышли два поезда. Скорость одного из них 63 км/час. Какова скорость второго, если поезда встретились через 4 часа?
Решение:
1) 63 * 4 = 252 (прошел 1 поезд)
2) 564 – 252 =312 (прошел 2 поезд)
3) 312 : 4 = 78
Решение в виде выражения (63 * 4 – 252) : 4 = 78
Ответ: Скорость второго поезда 78 км/час.
Задача 4
Два велосипедиста выехали навстречу друг другу. Скорость одного из низ 12 км/ч, а другого — 10 км/ч. Через 3 часа они встретились. Какое расстояние было между ними в начале пути?
Решение:
1) 12+10=22 (км/ч) скорость сближения велосипедистов
2) 22∙3=66 (км) было между велосипедистами в начале пути.
Ответ: Расстояние между велосипедистами в начале пути было 66 км.
Задача 5
Два поезда идут навстречу друг другу. Скорость одного из них 50 км/ч, скорость другого — 60 км/ч. Сейчас между ними 440 км. Через сколько часов они встретятся?
Решение:
1) 60+50=110 (км/ч) скорость сближения поездов
2) 440:110=4 (ч) время, через которое поезда встретятся.
Ответ: Поезда встретятся через 4 часа.
Движение в противоположных направлениях
Если два объекта движутся в противоположных направлениях, то они удаляются. Чтобы найти скорость удаления, надо сложить скорости этих объектов:
Скорость удаления больше скорости любого из них.
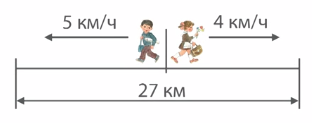
Задача 1
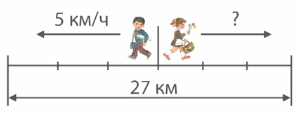
Из поселка вышли одновременно в противоположных направлениях два пешехода. Средняя скорость одного пешехода – 5 км/ч, другого – 4 км/ч. Через сколько часов расстояние между ними будет 27 км ?
Решение:
Чтобы найти время движения пешеходов, нужно знать расстояние и скорость пешеходов. Мы знаем, что за каждый час один пешеход удаляется от поселка на 5 км, а другой пешеход удаляется от поселка на 4 км. Можем найти их скорость удаления.
1.
(км/ч)
Мы знаем скорость удаления и знаем все расстояние – 27 км. Можем найти время, через которое пешеходы удалятся друг от друга на 27 км, для этого нужно расстояние разделить на скорость.
2.
(ч)
Ответ: Через три часа расстояние между переходами будет 27 км.
Задача 2
Из поселка вышли одновременно в противоположных направлениях два пешехода. Через 3 часа расстояние между ними было 27 км. Первый пешеход шел со скоростью 5 км/ч. С какой скоростью шел второй пешеход ?
Решение:
Чтобы узнать скорость второго пешехода, надо знать расстояние, которое он прошел, и его время в пути. Чтобы узнать, какое расстояние прошел второй пешеход, надо знать, какое расстояние прошел первый пешеход и общее расстояние. Общее расстояние мы знаем. Чтобы найти расстояние, которое прошел первый пешеход, надо знать его скорость и его время в пути. Средняя скорость движения первого пешехода – 5 км/ч, его время в пути – 3 часа. Если среднюю скорость умножить на время в пути, получим расстояние, которое прошел пешеход:
1.
(км)
Мы знаем общее расстояние и знаем расстояние, которое прошел первый пешеход. Можем теперь узнать, какое расстояние прошел второй пешеход.
2.
(км)
Теперь мы знаем расстояние, которое прошел второй пешеход, и время, проведенное им в пути. Можем найти его скорость.
3.
(км/ч)
Ответ: Скорость второго пешехода – 4 км/ч.
Задача 3
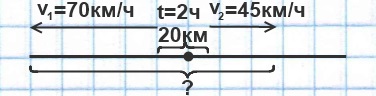
Товарный и пассажирский поезда движутся в противоположных направлениях. Скорость товарного 45 км/ч, скорость пассажирского — 70 км/ч. Сейчас между ними 20 км. Какое расстояние будет между ними через 2 часа ?
Решение:
1) 70+45=115 (км/ч) скорость удаления поездов
2) 115∙2=230 (км) пройдут поезда вместе за 2 часа
3) 230+20=250 (км) такое расстояние между поездами будет через 2 часа.
Ответ: Через 2 часа расстояние между поездами составит 250 км.
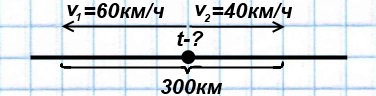
Задача 4
Из одного пункта одновременно в противоположных направлениях выехали два мотоциклиста. Скорость одного из них — 60 км/ч, скорость другого — 40 км/ч. Через какое время расстояние между ними станет равным 300 км?
Решение:
1) 60+40=100 (км/ч) скорость удаления мотоциклистов
2) 300:100=3 (ч) через такое время расстояние между ними будет 300 км.
Ответ: Расстояние между мотоциклистами станет 300 км через 3 часа.
Памятка “СКОРОСТЬ. ВРЕМЯ. РАССТОЯНИЕ.”
Скачать материал
Скачать материал


- Сейчас обучается 82 человека из 26 регионов


- Сейчас обучается 637 человек из 77 регионов


аудиоформат
- Сейчас обучается 138 человек из 47 регионов


Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 262 532 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 25.04.2018
- 334
- 0
- 25.04.2018
- 496
- 5
- 25.04.2018
- 2019
- 253
- 25.04.2018
- 369
- 4
- 25.04.2018
- 249
- 0
- 25.04.2018
- 638
- 1
- 25.04.2018
- 589
- 6
- 25.04.2018
- 223
- 0
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Сетевые и дистанционные (электронные) формы обучения в условиях реализации ФГОС по ТОП-50»
-
Курс повышения квалификации «Психолого-педагогические аспекты инклюзивного образования в условиях реализации ФГОС»
-
Курс повышения квалификации «Система образовательной организации в начальном общем образовании в условиях реализации ФГОС»
-
Курс повышения квалификации «Организация краеведческой деятельности детей в учебно-воспитательном процессе начальной школы»
-
Курс повышения квалификации «Содержательные аспекты профессионального и личностного развития педагогических работников в рамках реализации профессионального стандарта»
-
Курс повышения квалификации «Психолого-педагогическая диагностика в современном образовательном процессе»
-
Курс повышения квалификации «Разработка адаптированных образовательных программ в условиях ФГОС СПО»
-
Курс повышения квалификации «Организация работы с обучающимися с ограниченными возможностями здоровья (ОВЗ) в соответствии с ФГОС»
-
Курс повышения квалификации «Техники креативного мышления как инструмент формирования общих компетенций по ФГОС»
-
Курс повышения квалификации «Сурдопедагогика: организация обучения, воспитания, коррекция нарушений развития и социальной адаптации глухих, слабослышащих, позднооглохших обучающихся в условиях реализации программы ФГОС»
-
Курс повышения квалификации «Новые методы и технологии преподавания в начальной школе по ФГОС»
-
Курс повышения квалификации «Формирование и развитие ключевых компетенций школьников в интересах устойчивого развития региона»
-
Скачать материал
-
25.04.2018
10257
-
DOCX
15.1 кбайт -
371
скачивание -
Рейтинг:
5 из 5 -
Оцените материал:
-
-
Настоящий материал опубликован пользователем Цымбалюк Лариса Анатольевна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 7 лет и 4 месяца
- Подписчики: 2
- Всего просмотров: 662036
-
Всего материалов:
611