Как найти расстояние по прямой огэ математика

Найдите расстояние (по прямой) между противоположными углами обеденного стола. Ответ дайте в метрах квадратных.

Владелец собирается провести ремонт своей квартиры. На плане изображена предполагаемая расстановка мебели и бытовой техники на кухне после ремонта. Сторона каждой клетки равна 0,3 м. Кухня имеет квадратную форму. Единственная дверь кухни деревянная, в стене напротив двери расположено окно. Справа от двери будут поставлены полки для посуды, слева от двери будет смонтирована раковина для мытья посуды. В углу слева от окна предполагается разместить газовую плиту. Между раковиной и плитой будет собран буфет, отмеченный цифрой 3. Площадь, занятая буфетом, по плану будет равна 0,72 м2. В центре кухни планируется поставить обеденный стол. Кроме того, в угол кухни будет поставлен холодильник, занимающий 0,36 м2 пола. Пол кухни (в том числе там, где будет стоять мебель и бытовая техника) планируется покрыть плиткой размером 30 см × 30 см. Кроме того, владелец квартиры планирует смонтировать на кухне электрический подогрев пола. Чтобы сэкономить, владелец не станет подводить обогрев под холодильник, плиту, буфет, раковину и полки для посуды, а также на участок площадью 0,18 м2 между буфетом и плитой.

Весьма хитрая задача. На плане обозначен прямоугольный стол со сторонами 3 и 4 клеток, а длина измеряется не в квадратных метрах, а просто в метрах. Длина между углами данного стола представляет собой гипотенузу прямоугольного треугольника и равна корню квадратному из суммы квадратов катетов. Так гласит формула теоремы Пифагора. Подставляем значения:

√ (3²+ 4²) = √ (9 + 16) = √ (25) = 5. Конечно любой знакомый с математикой не станет это вычислять. Ведь перед ним магический квадрат – 3, 4, 5.

Теперь зная размер гипотенузы мы вычислим длину в метрах:

5 * 0.3 = 1.5 метра или 150 сантиметров или 15 дециметров.

автор вопроса выбрал этот ответ лучшим

Simple Ein
[190K]

более года назад

Из условия задачи понятно, что обеденный стол обозначен цифрой 4.

Обеденный стол со сторонами 3 и 4 клетки. Сторона каждой клетки равна 0,3 м.

Получается, одна сторона стола равна 0,3*3=0,9 м.

Вторая – 0,4*3=1,2 м.

Определить расстояние между противоположными углами у стола можно по теореме Пифагора.

Получается

√ (0,9²+ 1,2²) = √ (2,25) =1,5 метра.

Пашенька
[189K]

11 месяцев назад

Пояснение к задаче нам подсказывает, что обеденный стол на схеме расположен в центре кухни, поэтому можем смело утверждать, что нас интересует объект под номером 4.

Из условия задания нам известно, что клетка имеет размер – 0.3м.

Для подсчета нам необходимо рассчитать размеры стола. В клеточках это 3х4, в метрах:

3*0.3 = 0.9 – метра – одна сторона;
4*0.3 = 1.2 – метра – вторая сторона.

Далее учитываем, что стол – это прямоугольник, где расстояние между углами – это гипотенуза, а стороны стола – катеты.

Следовательно, на основании теоремы Пифагора мы имеем возможность рассчитать длину-гипотенузу.

Находим сумму квадратов катетов и извлекаем квадратный корень.

0.9*0.9 +1.2*1.2 = 0.81 + 1.44 = 2.25
Квадратный корень из 2.25
√2.25 = 1.5 – метра.

Ответ: 1.5.

Stan1711
[3.2K]

3 года назад

Длина измеряется в метрах.Из плана видно что размеры ободеного стола равны 3 клетки на 4.Стол прямоугльный.Тогда размер диагонали от одного угла до другого будет ровна 5 клеткам (как соотношение в прямоугольном треугольнике – 3:4:5.)Учитывая размер клетки 0,3м. мы получим ответ на вопрос 5*0,3 =1,5м.

Знаете ответ?

Источник

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.

На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до середины отрезка ВС. Ответ выразите в сантиметрах.

Источник: Диагностическая работа 01.10.2013 Вариант МА90105

Источник: Диагностическая работа 01.10.2013 Вариант МА90106

На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки А, В и С. Найдите расстояние от точки А до середины отрезка ВС. Ответ выразите в сантиметрах.

Пройти тестирование по этим заданиям

Источник

Здравствуйте, уважаемые читатели и учащиеся. Рассмотрим решение практико – ориентированных заданий по теме план местности. Задачи, которые были на пересдаче экзамена по математике в июле 2023 года и не вошли в решение этой статьи.

Ниже приводится текст задания:

План сельской местности в ОГЭ по матемтике.

Задание №1

Для ответа на это задание, необходимо внимательно читать текст задачи. Антоновка находится под цифрой 1. 1) Из Антоновки в Богданово (цифра 7) можно проехать по просёлочной дороге мимо реки (путь 1-7). 2) Есть другой путь – по шоссе до деревни Ванютино (цифра 4), где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Богданово (пусть 1-4-7). 3) Третий маршрут проходит по просёлочной дороге мимо пруда до деревни Горюново (цифра 6), где можно свернуть на шоссе до Богданово (путь 1-6-7). 4) Четвёртый маршрут пролегает по шоссе до деревни Доломино (цифра 3), от Доломино до Горюново (цифра 6) по просёлочной дороге мимо конюшни и от Горюново до Богданово по шоссе. 5) Ещё один маршрут проходит по шоссе до деревни Егорка (цифра 2), по просёлочной дороге мимо конюшни от Егорки до Жилино (цифра 5) и по шоссе от Жилино до Богданово. Сопоставим деревни с цифрами, получаем ответ: 7425

Задание №2. Найдите расстояние от Антоновки до Егорки по шоссе. Ответ дайте в километрах.

Отметим расстояния между деревнями на картинке

Найдем расстояние от Антоновки (цифра 1) до Егорки (цифра 2). Расстояние между деревнями 1 и 3 равно 12 км, расстояние между деревнями 2 и 3 равно 4 км, значит расстояние от Антоновки до Егорки равно 12-4 = 8 км

Задание №3 Найдите расстояние от Егорки до Жилино по прямой. Ответ дайте в километрах.

Расстояние от Егорки (цифра 2) до Жилино (цифра 5) по прямой, это отрезок между цифрами 2-5. Рассмотрим прямоугольный треугольник 2-4-5. Катет(2-4) равен 12 км, катет(4-5) равен 9 км. Расстояние между цифрами 2-5 равно:

Ответ 15.

Задание №4. Сколько минут затратят на дорогу Таня с дедушкой из Антоновки в Богданово, если поедут через Доломино и Горюново мимо конюшни?

Для решение этой задачи, необходимо найти расстояние из пункта 1 до пункта 3 (шоссе), от пункта 3 до 6 (проселочная работа), от пункта 6 до пункта 7 (шоссе).

1) Расстояние от пункта 1 до пункта 3 равно 12 км

2) Расстояние от пункта 3 до пункта 6 равно гипотенузе треугольника (3-4-6). Расстояние от пункта 3 до 4 равно 12-4=8 км; расстояние от пункта 4 до пункта 6 равно 15 км. Значит расстояние от пункта 3 до пункта 6 равно:

3)Расстояние между пунктом 6 и пунктом 7 равно 6 км (15 км – 9 км = 6 км (расстояние от 5 до 6 пункта), 12 км – 6 км = 6 км)

4)Найдем время, затраченное на дорогу. Скорость по шоссе равно 50 км/ч, по проселочной дороге 30 км/ч.

Ответ: 55,6

Задание №5. На просёлочных дорогах машина дедушки расходует 9,1 литра бензина на 100 км. Известно, что на путь из Антоновки до Богданово через Ванютино и путь через Горюново мимо пруда ей необходим один и тот же объём бензина. Сколько литров бензина на 100 км машина дедушки расходует на шоссе?

Решение. 1) Расстояние из Антоновки до Богданово через Ванютино составляет 41 км ((12+12-4)+(12+9)=41). Весь путь по шоссе.

2) Расстояние от Антоновки через Горюново до Богданово равно:

Здесь 25 км – это расстояние по проселочной дороге и 6 км по шоссе.

На 100 км по проселочной дороге необходимо 9,1 литра бензина. Составим выражение для нахождения объема бензина для движения по проселочной дороге из Антоновки до Горюново.

Составим выражения для расхода бензина по шоссе из Антоновки до Богданово через Ванютино и из Горюново до Богданово

Из условия задачи известно, что объем бензина, который необходим из Антоновки до Богданово через Ванютино и из Антоновки через Горюново до Богданово один и тот же, то составим уравнение:

Получаем, что расход бензина при движении по шоссе составляет 6,5 литра

Ответ. 6,5

Спасибо, что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.

Источник

ЗАДАНИЕ 22 ОГЭ. ТЕКСТОВЫЕ ЗАДАЧИ

Решение.

Пусть 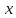км/ч – скорость пешехода, шедшего из пункта В, тогда км/ч – скорость пешехода, шедшего из пункта А. Так как пешеходы встретились в 9 км от пункта А, то пешеход, шедший из А прошёл 9 км, а пешеход, шедший из В прошёл 10 км. Значит, пешеход, шедший из А затратил на путь 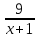ч, а пешеход, шедший из В – 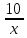ч. Поскольку пешеходы вышли одновременно, но пешеход, шедший из А сделал остановку на 30 мин = 0,5 ч, то составляем уравнение:

Учитывая невозможность отрицательной скорости, определяем ОДЗ.

ОДЗ, значит, скорость пешехода, шедшего из пункта В равна 5 км/ч, тогда скорость пешехода, шедшего из пункта А равна 6 км/ч.

Ответ: 6 км/ч.

Решение.

Пусть х км/ч – скорость пешехода, тогда скорость туриста – км/ч. До места встречи пешеход прошёл 10 км, а турист – 9 км. Пешеход на свой путь затратил 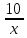ч, а турист затратил на свой путь 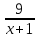ч. По условию задачи известно, что турист вышел на полчаса позже, т.е. затратил на 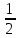ч меньше, чем пешеход.

Учитывая невозможность отрицательной скорости, определяем ОДЗ.

ОДЗ, значит, скорость пешехода равна 5 км/ч.

Ответ: 5 км/ч.

Решение.

Пусть S км – расстояние от А до С, v км/ч – скорость автомобиля. Тогда автомобиль затратил на путь от А до С 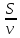ч, а мотоциклист – 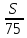ч. Так как мотоциклист выехал на 1 час 30 мин = 1,5 ч позже автомобиля, то 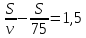. На обратный путь мотоциклист затратил столько же времени, сколько и на путь от А до С, т.е. 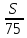ч. Пока мотоциклист ехал обратно, автомобиль продолжил движение от С до В и проехал 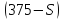км с той же скоростью, значит, затратил на этот путь ч. Поскольку в пункты А и В они прибыли одновременно, то времени на вторую часть пути затратили одинаковое количество. Поэтому . Составляем систему уравнений:

Решим второе уравнение.

не удовлетворяет условию задачи (скорость не может быть отрицательной), систему решаем только относительно .

Значит, скорость автомобиля равна 50 км/ч, а расстояние от А до С равно 225 км.

Ответ: 225 км.

Решение.

Пусть х км – расстояние от города А до места встречи. Тогда первый автомобиль проехал до места встречи х км, а второй – км. Поэтому первый автомобиль затратил на путь до места встречи ч, а второй – ч. По условию задачи известно, что второй автомобиль выехал на 3 часа позже первого. Составляем уравнение:

Значит, расстояние от города А до места встречи равно 400 км.

Ответ: 400 км.

Так как ж/д состав длиной 1 км проходит мимо неподвижной точки (в данном случае мимо столба) за 1 минуту, то это определяет его скорость, т.е. 1 км/мин. С этой скоростью за 3 минуты поезд проходит 3 км, из которых 1 км – это длина самого поезда. Поэтому длина туннеля 2 км.

Ответ: 2 км.

Решение.

Пусть х км/ч – скорость пешехода, тогда скорость велосипедиста км/ч. Так как они встретились в 8 км от пункта В, то пешеход прошёл 5 км, а велосипедист проехал 8 км до встречи. Пешеход затратил на свой путь ч, а велосипедист на свой путь затратил ч. Зная, что велосипедист в пути сделал остановку на 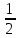ч, составляем уравнение:

, значит, скорость пешехода равна 5 км/ч.

Ответ: 5 км/ч.

Решение.

Так как поезд проезжает мимо движущегося в том же направлении пешехода, то скорость поезда относительно скорости пешехода равно . Значит, за 57 секунд поезд проедет м. Это и есть длина поезда.

Ответ: 950 м.

Решение.

С этой скоростью пассажирский поезд за 6 минут проедет , из которых – это длина товарного поезда. Значит, длина пассажирского поезда .

Решение.

Пусть х км – расстояние от города, из которого выехал второй велосипедист, до места встречи. Другими словами, это путь, который проехал второй велосипедист до места встречи. Тогда первый велосипедист до места встречи проехал км. На свой путь второй велосипедист затратил ч, а первый велосипедист на свой путь затратил ч. Так как по условию задачи известно, что первый велосипедист делал остановку на , то составляем уравнение:

Значит, расстояние от города, из которого выехал второй велосипедист, до места встречи равно 84 км.

Ответ: 84 км.

Решение.

Пусть х км/ч – скорость II велосипедиста, тогда км/ч – скорость I велосипедиста. Значит, первый велосипедист затратит на весь путь ч, а второй – ч. Зная, что первый прибывает к финишу на 3 часа раньше второго, составляем уравнение:

С учётом положительности скорости, определяем ОДЗ.

, значит, скорость второго велосипедиста равна 10 км/ч.

Ответ: 10 км/ч.

Решение.

Пусть км/ч – скорость третьего велосипедиста, а ч – время, затраченное третьим велосипедистом на путь от посёлка до места встречи со вторым велосипедистом. Тогда второй велосипедист затратил на путь до места встречи с третьим велосипедистом ч. Значит, третий проехал до места встречи со вторым км, а второй – км. Т.к. это одно и то же расстояние, получаем первое уравнение: .

Далее, третий велосипедист продолжил движение и через 4 часа догнал первого, значит, затратил на путь от посёлка до места встречи с первым – ч, а первый тогда затратил на весь путь от посёлка до места встречи с третьим велосипедистом ч, т.к. он ехал на 2 часа больше. Значит, третий велосипедист проехал от посёлка до места встречи с первым велосипедистом км, а первый соответственно – км. Эти расстояния также равны, поэтому получаем второе уравнение: . Составляем теперь систему двух уравнений:

не удовлетворяет смыслу задачи, т.к. в этом случае третий велосипедист не смог бы догнал не только первого, но и второго тоже. Значит, скорость третьего велосипедиста 24 км/ч.

Ответ: 24 км/ч.

Решение.

Пусть км – длина всего пути; км/ч – скорость первого автомобилиста на всём протяжении пути, тогда км/ч – скорость второго автомобилиста на первой половине пути. Значит, первый автомобилист затратил на весь путь 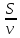ч, а второй автомобилист затратил на весь путь ч. Зная, что в пункт назначения они прибыли одновременно, составляем уравнение:

не удовлетворяет условию задачи (скорость первого автомобилиста должна быть больше 40 км/ч), значит, скорость первого автомобилиста равна 44 км/ч.

Ответ: 44 км/ч.

Решение.

Так как и мотоциклист, и велосипедист проезжают полностью весь путь от А до В, то примем этот пусть за 1. Пусть км/ч – скорость велосипедиста, а км/ч – скорость мотоциклиста. Тогда велосипедист проезжает весь путь за ч, а мотоциклист – за ч. Зная, что мотоциклист затратил на весь путь на меньше, чем велосипедист, составляем первое уравнение: .

Далее, за велосипедист проедет км, а мотоциклист – км. Поскольку по истечении этого времени они встретились, то совместно прошли весь путь, и поэтому: .

не удовлетворяет условию, значит, .

Итак, скорость велосипедиста равна 1 км/ч. Значит, на путь из В в А он затратил 1 ч.

Ответ: 1 ч.

Решение.

Средняя скорость тела – это отношение всего пути ко всему времени, затраченному на этот путь. Поэтому, находим длину всего пути и всё затраченное время:

Значит, средняя скорость автомобиля равна: км/ч.

Ответ: 75 км/ч.

Решение.

Пусть км/ч – скорость первого бегуна, тогда скорость второго бегуна км/ч. Тогда длина круга равна км. В тот момент, когда была озвучена информация о пробеге второго бегуна, первый был в пути 1 час, а второй – ч. По условию известно, что в тот момент разница по времени первого и второго бегуна составляет . Составляем уравнение:

Значит, скорость первого бегуна 13 км/ч.

Ответ: 13 км/ч.

Пусть 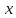км/ч – скорость велосипедиста из города А в город В. Тогда его скорость на обратном пути – км/ч. На путь из А в В велосипедист затратил ч, а на путь из В в А – ч. Зная, что на обратном пути велосипедист останавливался на 3 часа, и что общее время на путь из А в В и на путь из В в А одинаково, составляем уравнение:

Учитываем, что скорость положительна, т.е. .

не удовлетворяет условию, значит, скорость велосипедиста из города А в город В равна 10 км/ч.

Ответ: 10 км/ч.

Пусть 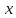км/ч – скорость туриста на спуске, тогда его скорость на подъёме – км/ч. За 2 часа на спуске турист прошёл км, а за оставшиеся 2 часа на подъёме он прошёл км. Зная, что весь путь равен 14 км, составляем уравнение:

Значит, скорость туриста на спуске равна 5 км/ч.

Ответ: 5 км/ч.

Пусть 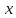км – расстояние от точки отправления до места встречи, тогда первый человек прошёл до места встречи 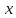км, а второй человек (который шёл с большей скоростью) прошёл до места встречи км. Первый затратил на свой путь ч, а второй затратил на свой путь ч. Так как время, которое затратил каждый из них одинаково, составляем уравнение:

Значит, расстояние от точки отправления до места встречи равно 3 км.

Ответ: 3 км.

(152, 314608) Из пунктов А и В, расстояние между которыми 27 км, вышли одновременно навстречу друг другу два пешехода и встретились в 15 км от А. Найдите скорость пешехода, шедшего из А, если известно, что он шёл со скоростью, на 2 км/ч большей, чем пешеход, шедший из В, и сделал в пути получасовую остановку.

(314513) Из пунктов А и В, расстояние между которыми 19 км, вышли одновременно навстречу друг другу два туриста и встретились в 10 км от В. Турист, шедший из А сделал в пути получасовую остановку. Найдите скорость туриста, шедшего из В, если известно, что он шёл со скоростью, на 1 км/ч меньшей, чем турист, шедший из А.

(314514) Из пунктов А и В, расстояние между которыми 27 км, вышли одновременно навстречу друг другу два туриста и встретились в 12 км от В. Турист, шедший из А сделал в пути получасовую остановку. Найдите скорость пешехода, шедшего из В, если известно, что он шёл со скоростью, на 2 км/ч меньшей, чем первый турист.

(314559) Из пункта А в пункт В, расстояние между которыми 19 км, вышел турист. Через полчаса навстречу ему из пункта В вышел пешеход и встретил туриста в 12 км от А. Найдите скорость туриста, если известно, что она была на 2 км/ч меньше скорости пешехода.

(311922) Расстояние от города до посёлка равно 120 км. Из города в посёлок выехал автобус. Через час после этого вслед за ним выехал автомобиль, скорость которого на 10 км/ч больше скорости автобуса. Найдите скорость автобуса (в км/ч), если известно, что в пути он сделал остановку на 24 минуты, а в посёлок автомобиль и автобус прибыли одновременно.

(338945) Расстояние между городами А и В равно 120 км. Из города А в город В выехал автомобиль, а через 90 минут следом за ним со скоростью 100 км/ч выехал мотоциклист. Мотоциклист догнал автомобиль в городе С и повернул обратно. Когда он проехал половину пути из С в А, автомобиль прибыл в В. Найдите расстояние от А до С.

(353092) Расстояние между городами А и В равно 120 км. Город С находится между городами А и В. Из города А в город В выехал автомобиль, а через 36 минут следом за ним со скоростью 75 км/ч выехал мотоциклист, догнал автомобиль в городе С и повернул обратно. Когда он проехал половину пути из С в А, автомобиль прибыл в В. Найдите расстояние от А до С.

(348881) Расстояние между городами А и В равно 100 км. Из города А в город В выехал автомобиль, а через 60 минут следом за ним со скоростью 80 км/ч выехал мотоциклист. Мотоциклист догнал автомобиль в городе С и повернул обратно. Когда он проехал половину пути из С в А, автомобиль прибыл в В. Найдите расстояние от А до С.

(349070) Расстояние между городами А и В равно 70 км. Из города А в город В выехал автомобиль, а через 15 минут следом за ним со скоростью 50 км/ч выехал мотоциклист. Мотоциклист догнал автомобиль в городе С и повернул обратно. Когда он проехал половину пути из С в А, автомобиль прибыл в В. Найдите расстояние от А до С.

(349089) Расстояние между городами А и В равно 130 км. Из города А в город В выехал автомобиль, а через 15 минут следом за ним со скоростью 45 км/ч выехал мотоциклист. Мотоциклист догнал автомобиль в городе С и повернул обратно. Когда он проехал половину пути из С в А, автомобиль прибыл в В. Найдите расстояние от А до С.

(349298) Расстояние между городами А и В равно 140 км. Из города А в город В выехал автомобиль, а через 30 минут следом за ним со скоростью 50 км/ч выехал мотоциклист. Мотоциклист догнал автомобиль в городе С и повернул обратно. Когда он проехал половину пути из С в А, автомобиль прибыл в В. Найдите расстояние от А до С.

(349744) Расстояние между городами А и В равно 120 км. Из города А в город В выехал автомобиль, а через 60 минут следом за ним со скоростью 45 км/ч выехал мотоциклист. Мотоциклист догнал автомобиль в городе С и повернул обратно. Когда он проехал половину пути из С в А, автомобиль прибыл в В. Найдите расстояние от А до С.

(350017) Расстояние между городами А и В равно 80 км. Из города А в город В выехал автомобиль, а через 30 минут следом за ним со скоростью 60 км/ч выехал мотоциклист. Мотоциклист догнал автомобиль в городе С и повернул обратно. Когда он проехал половину пути из С в А, автомобиль прибыл в В. Найдите расстояние от А до С.

(351128) Расстояние между городами А и В равно 120 км. Из города А в город В выехал автомобиль, а через 30 минут следом за ним со скоростью 90 км/ч выехал мотоциклист. Мотоциклист догнал автомобиль в городе С и повернул обратно. Когда он проехал половину пути из С в А, автомобиль прибыл в В. Найдите расстояние от А до С.

(351193) Расстояние между городами А и В равно 120 км. Из города А в город В выехал автомобиль, а через 120 минут следом за ним со скоростью 75 км/ч выехал мотоциклист. Мотоциклист догнал автомобиль в городе С и повернул обратно. Когда он проехал половину пути из С в А, автомобиль прибыл в В. Найдите расстояние от А до С.

(352334) Расстояние между городами А и В равно 120 км. Из города А в город В выехал автомобиль, а через 45 минут следом за ним со скоростью 60 км/ч выехал мотоциклист. Мотоциклист догнал автомобиль в городе С и повернул обратно. Когда он проехал половину пути из С в А, автомобиль прибыл в В. Найдите расстояние от А до С.

(352340) Расстояние между городами А и В равно 100 км. Из города А в город В выехал автомобиль, а через 48 минут следом за ним со скоростью 100 км/ч выехал мотоциклист. Мотоциклист догнал автомобиль в городе С и повернул обратно. Когда он проехал половину пути из С в А, автомобиль прибыл в В. Найдите расстояние от А до С.

(352355) Расстояние между городами А и В равно 100 км. Из города А в город В выехал автомобиль, а через 75 минут следом за ним со скоростью 64 км/ч выехал мотоциклист. Мотоциклист догнал автомобиль в городе С и повернул обратно. Когда он проехал половину пути из С в А, автомобиль прибыл в В. Найдите расстояние от А до С.

(352864) Расстояние между городами А и В равно 110 км. Из города А в город В выехал автомобиль, а через 75 минут следом за ним со скоростью 90 км/ч выехал мотоциклист. Мотоциклист догнал автомобиль в городе С и повернул обратно. Когда он проехал половину пути из С в А, автомобиль прибыл в В. Найдите расстояние от А до С.

(352997) Расстояние между городами А и В равно 90 км. Из города А в город В выехал автомобиль, а через 45 минут следом за ним со скоростью 70 км/ч выехал мотоциклист. Мотоциклист догнал автомобиль в городе С и повернул обратно. Когда он проехал половину пути из С в А, автомобиль прибыл в В. Найдите расстояние от А до С.

(311601) Расстояние между городами А и В равно 490 км. Из города А в город В со скоростью 55 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города В выехал со скоростью 90 км/ч второй автомобиль. На каком расстоянии от города А автомобили встретятся?

(314516) Из пункта А в пункт В, расстояние между которыми 13 км, вышел пешеход. Одновременно с ним из В в А выехал велосипедист. Велосипедист ехал со скоростью, на 11 км/ч большей скорости пешехода, и сделал в пути получасовую остановку. Найдите скорость велосипедиста, если известно, что они встретились в 5 км от А.

(314561) Из пункта А в пункт В, расстояние между которыми 34 км, выехал велосипедист. Одновременно навстречу ему из В в А вышел пешеход. Велосипедист ехал со скоростью, на 8 км/ч большей скорости пешехода, и сделал в пути получасовую остановку. Найдите скорость пешехода, если известно, что они встретились в 24 км от пункта А.

(314566) Из пункта А в пункт В, расстояние между которыми 13 км, вышел пешеход. Через полчаса навстречу ему из В в А выехал велосипедист. Велосипедист ехал со скоростью, на 11 км/ч большей скорости пешехода. Найдите скорость велосипедиста, если известно, что они встретились в 5 км от пункта А.

(314606) Из пункта А в пункт В, расстояние между которыми 34 км, вышел пешеход. Через полчаса навстречу ему из В в А выехал велосипедист. Велосипедист ехал со скоростью, на 8 км/ч большей скорости пешехода. Найдите скорость велосипедиста, если известно, что они встретились в 10 км от пункта А.

(314593) Из пункта А в пункт В, расстояние между которыми 34 км, выехал велосипедист. Одновременно с ним из В в А вышел пешеход. Велосипедист ехал со скоростью, на 8 км/ч большей скорости пешехода, и сделал в пути получасовую остановку. Найдите скорость велосипедиста, если известно, что они встретились в 10 км от пункта В.

(338854) Поезд, двигаясь равномерно со скоростью 75 км/ч, проезжает мимо пешехода, идущего параллельно путям, со скоростью 3 км/ч навстречу поезду, за 30 секунд. Найдите длину поезда в метрах.

(341283, 349640) Поезд, двигаясь равномерно со скоростью 86 км/ч, проезжает мимо идущего в том же направлении, параллельно путям, со скоростью 6 км/ч пешехода, за 18 секунд. Найдите длину поезда в метрах.

(341288, 349359) Поезд, двигаясь равномерно со скоростью 44 км/ч, проезжает мимо идущего в том же направлении, параллельно путям, со скоростью 4 км/ч пешехода, за 81 секунду. Найдите длину поезда в метрах.

(348526) Поезд, двигаясь равномерно со скоростью 87 км/ч, проезжает мимо пешехода, идущего параллельно путям, со скоростью 3 км/ч навстречу поезду, за 24 секунды. Найдите длину поезда в метрах.

(348814) Поезд, двигаясь равномерно со скоростью 36 км/ч, проезжает мимо пешехода, идущего параллельно путям, со скоростью 4 км/ч навстречу поезду, за 54 секунды. Найдите длину поезда в метрах.

(348978) Поезд, двигаясь равномерно со скоростью 74 км/ч, проезжает мимо пешехода, идущего параллельно путям, со скоростью 6 км/ч навстречу поезду, за 18 секунд. Найдите длину поезда в метрах.

(349163) Поезд, двигаясь равномерно со скоростью 57 км/ч, проезжает мимо пешехода, идущего параллельно путям, со скоростью 3 км/ч навстречу поезду, за 36 секунд. Найдите длину поезда в метрах.

(349311) Поезд, двигаясь равномерно со скоростью 26 км/ч, проезжает мимо пешехода, идущего параллельно путям, со скоростью 4 км/ч навстречу поезду, за 90 секунд. Найдите длину поезда в метрах.

(349565) Поезд, двигаясь равномерно со скоростью 57 км/ч, проезжает мимо пешехода, идущего параллельно путям, со скоростью 3 км/ч навстречу поезду, за 33 секунды. Найдите длину поезда в метрах.

(349680) Поезд, двигаясь равномерно со скоростью 129 км/ч, проезжает мимо пешехода, идущего параллельно путям, со скоростью 6 км/ч навстречу поезду, за 12 секунд. Найдите длину поезда в метрах.

(349702) Поезд, двигаясь равномерно со скоростью 87 км/ч, проезжает мимо пешехода, идущего параллельно путям, со скоростью 3 км/ч навстречу поезду, за 32 секунды. Найдите длину поезда в метрах.

(349757) Поезд, двигаясь равномерно со скоростью 66 км/ч, проезжает мимо пешехода, идущего параллельно путям, со скоростью 6 км/ч навстречу поезду, за 10 секунд. Найдите длину поезда в метрах.

(349884) Поезд, двигаясь равномерно со скоростью 87 км/ч, проезжает мимо пешехода, идущего параллельно путям, со скоростью 3 км/ч навстречу поезду, за 8 секунд. Найдите длину поезда в метрах.

(350372) Поезд, двигаясь равномерно со скоростью 129 км/ч, проезжает мимо пешехода, идущего параллельно путям, со скоростью 6 км/ч навстречу поезду, за 8 секунд. Найдите длину поезда в метрах.

(350843) Поезд, двигаясь равномерно со скоростью 36 км/ч, проезжает мимо пешехода, идущего параллельно путям, со скоростью 4 км/ч навстречу поезду, за 36 секунд. Найдите длину поезда в метрах.

(351087) Поезд, двигаясь равномерно со скоростью 140 км/ч, проезжает мимо пешехода, идущего параллельно путям, со скоростью 4 км/ч навстречу поезду, за 10 секунд. Найдите длину поезда в метрах.

(351147) Поезд, двигаясь равномерно со скоростью 57 км/ч, проезжает мимо пешехода, идущего параллельно путям, со скоростью 3 км/ч навстречу поезду, за 18 секунд. Найдите длину поезда в метрах.

(351178) Поезд, двигаясь равномерно со скоростью 57 км/ч, проезжает мимо пешехода, идущего параллельно путям, со скоростью 3 км/ч навстречу поезду, за 39 секунды. Найдите длину поезда в метрах.

(352522) Поезд, двигаясь равномерно со скоростью 151 км/ч, проезжает мимо пешехода, идущего параллельно путям, со скоростью 5 км/ч навстречу поезду, за 15 секунд. Найдите длину поезда в метрах.

(352783) Поезд, двигаясь равномерно со скоростью 36 км/ч, проезжает мимо пешехода, идущего параллельно путям, со скоростью 4 км/ч навстречу поезду, за 81 секунду. Найдите длину поезда в метрах.

(353127) Поезд, двигаясь равномерно со скоростью 51 км/ч, проезжает мимо пешехода, идущего параллельно путям, со скоростью 3 км/ч навстречу поезду, за 50 секунд. Найдите длину поезда в метрах.

(353306) Поезд, двигаясь равномерно со скоростью 177 км/ч, проезжает мимо пешехода, идущего параллельно путям, со скоростью 3 км/ч навстречу поезду, за 13 секунд. Найдите длину поезда в метрах.

(333102) Поезд, двигаясь равномерно со скоростью 57 км/ч, проезжает мимо идущего в том же направлении, параллельно путям, со скоростью 5 км/ч пешехода, за 45 секунд. Найдите длину поезда в метрах.

(353554) Поезд, двигаясь равномерно со скоростью 141 км/ч, проезжает мимо идущего в том же направлении, параллельно путям, со скоростью 6 км/ч пешехода, за 8 секунд. Найдите длину поезда в метрах.

(348607) Поезд, двигаясь равномерно со скоростью 93 км/ч, проезжает мимо идущего в том же направлении, параллельно путям, со скоростью 3 км/ч пешехода, за 32 секунды. Найдите длину поезда в метрах.

(348902) Поезд, двигаясь равномерно со скоростью 148 км/ч, проезжает мимо идущего в том же направлении, параллельно путям, со скоростью 4 км/ч пешехода, за 10 секунд. Найдите длину поезда в метрах.

(349007) Поезд, двигаясь равномерно со скоростью 183 км/ч, проезжает мимо идущего в том же направлении, параллельно путям, со скоростью 3 км/ч пешехода, за 13 секунд. Найдите длину поезда в метрах.

(349069) Поезд, двигаясь равномерно со скоростью 93 км/ч, проезжает мимо идущего в том же направлении, параллельно путям, со скоростью 3 км/ч пешехода, за 24 секунды. Найдите длину поезда в метрах.

(349633) Поезд, двигаясь равномерно со скоростью 34 км/ч, проезжает мимо идущего в том же направлении, параллельно путям, со скоростью 4 км/ч пешехода, за 90 секунд. Найдите длину поезда в метрах.

(349669) Поезд, двигаясь равномерно со скоростью 93 км/ч, проезжает мимо идущего в том же направлении, параллельно путям, со скоростью 3 км/ч пешехода, за 8 секунд. Найдите длину поезда в метрах.

(350199) Поезд, двигаясь равномерно со скоростью 63 км/ч, проезжает мимо идущего в том же направлении, параллельно путям, со скоростью 3 км/ч пешехода, за 39 секунд. Найдите длину поезда в метрах.

(350272) Поезд, двигаясь равномерно со скоростью 78 км/ч, проезжает мимо идущего в том же направлении, параллельно путям, со скоростью 6 км/ч пешехода, за 10 секунд. Найдите длину поезда в метрах.

(350477) Поезд, двигаясь равномерно со скоростью 141 км/ч, проезжает мимо идущего в том же направлении, параллельно путям, со скоростью 6 км/ч пешехода, за 12 секунд. Найдите длину поезда в метрах.

(350804) Поезд, двигаясь равномерно со скоростью 44 км/ч, проезжает мимо идущего в том же направлении, параллельно путям, со скоростью 4 км/ч пешехода, за 36 секунд. Найдите длину поезда в метрах.

(351182) Поезд, двигаясь равномерно со скоростью 63 км/ч, проезжает мимо идущего в том же направлении, параллельно путям, со скоростью 3 км/ч пешехода, за 36 секунд. Найдите длину поезда в метрах.

(352267) Поезд, двигаясь равномерно со скоростью 63 км/ч, проезжает мимо идущего в том же направлении, параллельно путям, со скоростью 3 км/ч пешехода, за 18 секунд. Найдите длину поезда в метрах.

(352404) Поезд, двигаясь равномерно со скоростью 44 км/ч, проезжает мимо идущего в том же направлении, параллельно путям, со скоростью 4 км/ч пешехода, за 54 секунд. Найдите длину поезда в метрах.

(352637) Поезд, двигаясь равномерно со скоростью 161 км/ч, проезжает мимо идущего в том же направлении, параллельно путям, со скоростью 5 км/ч пешехода, за 15 секунд. Найдите длину поезда в метрах.

(352967) Поезд, двигаясь равномерно со скоростью 63 км/ч, проезжает мимо идущего в том же направлении, параллельно путям, со скоростью 3 км/ч пешехода, за 33 секунды. Найдите длину поезда в метрах.

(353114) Поезд, двигаясь равномерно со скоростью 57 км/ч, проезжает мимо идущего в том же направлении, параллельно путям, со скоростью 3 км/ч пешехода, за 50 секунд. Найдите длину поезда в метрах.

(333155) По двум параллельным железнодорожным путям в одном направлении следуют товарный и пассажирский поезда, скорости которых равны соответственно 40 км/ч и 100 км/ч. Длина товарного поезда равна 750 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 1 минуте.

(338998) По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 50 км/ч и 40 км/ч. Длина товарного поезда равна 1350 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 9 минутам. Ответ дайте в метрах.

(348624) По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 100 км/ч и 90 км/ч. Длина товарного поезда равна 800 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 6 минутам.

(349567) По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 170 км/ч и 80 км/ч. Длина товарного поезда равна 850 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 1 минуте.

(349766) По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 90 км/ч и 40 км/ч. Длина товарного поезда равна 1650 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 3 минутам.

(349810) По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 40 км/ч и 30 км/ч. Длина товарного поезда равна 1800 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 15 минутам.

(350269) По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 50 км/ч и 40 км/ч. Длина товарного поезда равна 1600 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 15 минутам.

(350950) По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 60 км/ч и 30 км/ч. Длина товарного поезда равна 600 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 2 минутам.

(351132) По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 190 км/ч и 40 км/ч. Длина товарного поезда равна 1550 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 1 минуте.

(351244) По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 190 км/ч и 70 км/ч. Длина товарного поезда равна 1400 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 1 минуте.

(351524) По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 40 км/ч и 30 км/ч. Длина товарного поезда равна 800 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 6 минутам.

(352203) По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 60 км/ч и 40 км/ч. Длина товарного поезда равна 1700 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 6 минутам.

(352269) По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 60 км/ч и 30 км/ч. Длина товарного поезда равна 1300 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 3 минутам.

(352575) По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 140 км/ч и 90 км/ч. Длина товарного поезда равна 1650 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 3 минутам.

(352761) По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 110 км/ч и 70 км/ч. Длина товарного поезда равна 1800 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 3 минутам.

(352762) По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 40 км/ч и 30 км/ч. Длина товарного поезда равна 850 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 9 минутам.

(353194) По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 150 км/ч и 30 км/ч. Длина товарного поезда равна 1150 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 1 минуте.

(353299) По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 130 км/ч и 80 км/ч. Длина товарного поезда равна 1900 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 3 минутам.

(353314) По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 120 км/ч и 80 км/ч. Длина товарного поезда равна 1250 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 3 минутам.

(353404) По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 70 км/ч и 50 км/ч. Длина товарного поезда равна 700 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 3 минутам.

(353577) По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 60 км/ч и 30 км/ч. Длина товарного поезда равна 900 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 3 минутам.

(338867) Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 36 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 82 км, скорость первого велосипедиста равна 28 км/ч, а скорость второго – 10 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.

(333345) Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 40 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 92 км, скорость первого велосипедиста равна 30 км/ч, а скорость второго – 12 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.

(348713) Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 48 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 119 км, скорость первого велосипедиста равна 20 км/ч, а скорость второго – 30 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.

(349149) Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 28 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 286 км, скорость первого велосипедиста равна 10 км/ч, а скорость второго – 30 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.

(349228) Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 44 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 141 км, скорость первого велосипедиста равна 24 км/ч, а скорость второго – 15 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.

(350944) Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 32 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 312 км, скорость первого велосипедиста равна 10 км/ч, а скорость второго – 30 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.

(350975) Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 20 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 210 км, скорость первого велосипедиста равна 20 км/ч, а скорость второго – 30 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.

(351309) Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 56 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 93 км, скорость первого велосипедиста равна 20 км/ч, а скорость второго – 30 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.

(351422) Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 2 минуты, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 277 км, скорость первого велосипедиста равна 16 км/ч, а скорость второго – 30 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.

(351500) Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 35 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 126 км, скорость первого велосипедиста равна 16 км/ч, а скорость второго – 12 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.

(351907) Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 24 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 227 км, скорость первого велосипедиста равна 20 км/ч, а скорость второго – 30 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.

(351983) Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 16 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 116 км, скорость первого велосипедиста равна 15 км/ч, а скорость второго – 30 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.

(351996) Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 36 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 120 км, скорость первого велосипедиста равна 10 км/ч, а скорость второго – 20 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.

(352521) Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 10 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 102 км, скорость первого велосипедиста равна 18 км/ч, а скорость второго – 24 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.

(352935) Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 26 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 217 км, скорость первого велосипедиста равна 21 км/ч, а скорость второго – 30 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.

(353052) Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 52 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 198 км, скорость первого велосипедиста равна 10 км/ч, а скорость второго – 15 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.

(353126) Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 35 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 179 км, скорость первого велосипедиста равна 16 км/ч, а скорость второго – 24 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.

(353266) Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 48 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 168 км, скорость первого велосипедиста равна 15 км/ч, а скорость второго – 30 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.

(353319) Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 27 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 195 км, скорость первого велосипедиста равна 11 км/ч, а скорость второго – 20 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.

(353550) Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 56 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 182 км, скорость первого велосипедиста равна 13 км/ч, а скорость второго – 15 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.

(353582) Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 51 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 251 км, скорость первого велосипедиста равна 10 км/ч, а скорость второго – 20 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.

(338972) Два автомобиля одновременно отправляются в 240-километровый пробег. Первый едет со скоростью, на 20 км/ч большей, чем второй, и прибывает к финишу на 1 час раньше второго. Найдите скорость первого автомобиля.

(353275) Два велосипедиста одновременно отправляются в 180-километровый пробег. Первый едет со скоростью, на 5 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу первым.

(348509) Два велосипедиста одновременно отправляются в 60-километровый пробег. Первый едет со скоростью, на 10 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу первым.

(348536) Два велосипедиста одновременно отправляются в 224-километровый пробег. Первый едет со скоростью, на 2 км/ч большей, чем второй, и прибывает к финишу на 2 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.

(348749) Два велосипедиста одновременно отправляются в 180-километровый пробег. Первый едет со скоростью, на 5 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.

(349549) Два велосипедиста одновременно отправляются в 105-километровый пробег. Первый едет со скоростью, на 16 км/ч большей, чем второй, и прибывает к финишу на 4 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.

(349790) Два велосипедиста одновременно отправляются в 208-километровый пробег. Первый едет со скоростью, на 3 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу первым.

(350116) Два велосипедиста одновременно отправляются в 209-километровый пробег. Первый едет со скоростью, на 8 км/ч большей, чем второй, и прибывает к финишу на 8 часов раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.

(350503) Два велосипедиста одновременно отправляются в 224-километровый пробег. Первый едет со скоростью, на 2 км/ч большей, чем второй, и прибывает к финишу на 2 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу первым.

(350783) Два велосипедиста одновременно отправляются в 209-километровый пробег. Первый едет со скоростью, на 8 км/ч большей, чем второй, и прибывает к финишу на 8 часов раньше второго. Найдите скорость велосипедиста, пришедшего к финишу первым.

(351108) Два велосипедиста одновременно отправляются в 112-километровый пробег. Первый едет со скоростью, на 9 км/ч большей, чем второй, и прибывает к финишу на 4 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу первым.

(351344) Два велосипедиста одновременно отправляются в 208-километровый пробег. Первый едет со скоростью, на 3 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.

(351624) Два велосипедиста одновременно отправляются в 105-километровый пробег. Первый едет со скоростью, на 16 км/ч большей, чем второй, и прибывает к финишу на 4 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу первым.

(351674) Два велосипедиста одновременно отправляются в 100-километровый пробег. Первый едет со скоростью, на 15 км/ч большей, чем второй, и прибывает к финишу на 6 часов раньше второго. Найдите скорость велосипедиста, пришедшего к финишу первым.

(351821) Два велосипедиста одновременно отправляются в 140-километровый пробег. Первый едет со скоростью, на 6 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.

(351959) Два велосипедиста одновременно отправляются в 140-километровый пробег. Первый едет со скоростью, на 6 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу первым.

(352459) Два велосипедиста одновременно отправляются в 140-километровый пробег. Первый едет со скоростью, на 14 км/ч большей, чем второй, и прибывает к финишу на 5 часов раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.

(352504) Два велосипедиста одновременно отправляются в 100-километровый пробег. Первый едет со скоростью, на 15 км/ч большей, чем второй, и прибывает к финишу на 6 часов раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.

(352850) Два велосипедиста одновременно отправляются в 112-километровый пробег. Первый едет со скоростью, на 9 км/ч большей, чем второй, и прибывает к финишу на 4 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.

(353026) Два велосипедиста одновременно отправляются в 140-километровый пробег. Первый едет со скоростью, на 14 км/ч большей, чем второй, и прибывает к финишу на 5 часов раньше второго. Найдите скорость велосипедиста, пришедшего к финишу первым.

(353551) Два автомобиля одновременно отправляются в 420-километровый пробег. Первый едет со скоростью, на 24 км/ч большей, чем второй, и прибывает к финишу на 2 часа раньше второго. Найдите скорость первого автомобиля.

(348552) Два автомобиля одновременно отправляются в 780-километровый пробег. Первый едет со скоростью, на 13 км/ч большей, чем второй, и прибывает к финишу на 2 часа раньше второго. Найдите скорость первого автомобиля.

(348585) Два автомобиля одновременно отправляются в 720-километровый пробег. Первый едет со скоростью, на 30 км/ч большей, чем второй, и прибывает к финишу на 4 часа раньше второго. Найдите скорость первого автомобиля.

(348737) Два автомобиля одновременно отправляются в 840-километровый пробег. Первый едет со скоростью, на 4 км/ч большей, чем второй, и прибывает к финишу на 1 час раньше второго. Найдите скорость первого автомобиля.

(349005) Два автомобиля одновременно отправляются в 800-километровый пробег. Первый едет со скоростью, на 36 км/ч большей, чем второй, и прибывает к финишу на 5 часов раньше второго. Найдите скорость первого автомобиля.

(349393) Два автомобиля одновременно отправляются в 990-километровый пробег. Первый едет со скоростью, на 33 км/ч большей, чем второй, и прибывает к финишу на 5 часов раньше второго. Найдите скорость первого автомобиля.

(349413) Два автомобиля одновременно отправляются в 660-километровый пробег. Первый едет со скоростью, на 11 км/ч большей, чем второй, и прибывает к финишу на 2 часа раньше второго. Найдите скорость первого автомобиля.

(349491) Два автомобиля одновременно отправляются в 760-километровый пробег. Первый едет со скоростью, на 19 км/ч большей, чем второй, и прибывает к финишу на 2 часа раньше второго. Найдите скорость первого автомобиля.

(349781) Два автомобиля одновременно отправляются в 900-километровый пробег. Первый едет со скоростью, на 40 км/ч большей, чем второй, и прибывает к финишу на 8 часов раньше второго. Найдите скорость первого автомобиля.

(350025) Два автомобиля одновременно отправляются в 950-километровый пробег. Первый едет со скоростью, на 18 км/ч большей, чем второй, и прибывает к финишу на 4 часа раньше второго. Найдите скорость первого автомобиля.

(350529) Два автомобиля одновременно отправляются в 990-километровый пробег. Первый едет со скоростью, на 9 км/ч большей, чем второй, и прибывает к финишу на 1 час раньше второго. Найдите скорость первого автомобиля.

(350530) Два автомобиля одновременно отправляются в 810-километровый пробег. Первый едет со скоростью, на 36 км/ч большей, чем второй, и прибывает к финишу на 6 часов раньше второго. Найдите скорость первого автомобиля.

(350535) Два автомобиля одновременно отправляются в 630-километровый пробег. Первый едет со скоростью, на 24 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость первого автомобиля.

(350764) Два автомобиля одновременно отправляются в 980-километровый пробег. Первый едет со скоростью, на 28 км/ч большей, чем второй, и прибывает к финишу на 4 часа раньше второго. Найдите скорость первого автомобиля.

(351284) Два автомобиля одновременно отправляются в 930-километровый пробег. Первый едет со скоростью, на 31 км/ч большей, чем второй, и прибывает к финишу на 5 часов раньше второго. Найдите скорость первого автомобиля.

(351306) Два автомобиля одновременно отправляются в 560-километровый пробег. Первый едет со скоростью, на 10 км/ч большей, чем второй, и прибывает к финишу на 1 час раньше второго. Найдите скорость первого автомобиля.

(352210) Два автомобиля одновременно отправляются в 800-километровый пробег. Первый едет со скоростью, на 20 км/ч большей, чем второй, и прибывает к финишу на 2 часа раньше второго. Найдите скорость первого автомобиля.

(352845) Два автомобиля одновременно отправляются в 540-километровый пробег. Первый едет со скоростью, на 30 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость первого автомобиля.

(353442) Два автомобиля одновременно отправляются в 570-километровый пробег. Первый едет со скоростью, на 16 км/ч большей, чем второй, и прибывает к финишу на 2 часа раньше второго. Найдите скорость первого автомобиля.

(353302) Первый велосипедист выехал из посёлка по шоссе со скоростью 21 км/ч. Через час после него со скоростью 15 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час – третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 9 часов после этого догнал первого.

(348434) Первый велосипедист выехал из посёлка по шоссе со скоростью 24 км/ч. Через час после него со скоростью 21 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час – третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 9 часов после этого догнал первого.

(349632) Первый велосипедист выехал из посёлка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 10 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час – третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 5 часов после этого догнал первого.

(349923) Первый велосипедист выехал из посёлка по шоссе со скоростью 22 км/ч. Через час после него со скоростью 12 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час – третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 8 часов после этого догнал первого.

(350489) Первый велосипедист выехал из посёлка по шоссе со скоростью 20 км/ч. Через час после него со скоростью 16 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час – третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 8 часов после этого догнал первого.

(352768) Первый велосипедист выехал из посёлка по шоссе со скоростью 12 км/ч. Через час после него со скоростью 10 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час – третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа после этого догнал первого.

(341128) Из А и В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал половину пути со скоростью, меньшей скорости первого автомобилиста на 9 км/ч, а вторую половину пути ехал со скоростью 60 км/ч, в результате чего прибыл в В одновременно первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 40 км/ч.

(351543) Из А и В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал половину пути со скоростью 30 км/ч, а вторую половину пути проехал со скоростью, большей скорости первого автомобилиста на 9 км/ч, в результате чего прибыл в В одновременно первым автомобилистом. Найдите скорость первого автомобилиста.

(348652) Из А и В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал половину пути со скоростью 36 км/ч, а вторую половину пути проехал со скоростью, большей скорости первого автомобилиста на 54 км/ч, в результате чего прибыл в В одновременно первым автомобилистом. Найдите скорость первого автомобилиста.

(349353) Из А и В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал половину пути со скоростью 55 км/ч, а вторую половину пути проехал со скоростью, большей скорости первого автомобилиста на 6 км/ч, в результате чего прибыл в В одновременно первым автомобилистом. Найдите скорость первого автомобилиста.

(351137) Из А и В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал половину пути со скоростью 51 км/ч, а вторую половину пути проехал со скоростью, большей скорости первого автомобилиста на 34 км/ч, в результате чего прибыл в В одновременно первым автомобилистом. Найдите скорость первого автомобилиста.

(351369) Из А и В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал половину пути со скоростью 70 км/ч, а вторую половину пути проехал со скоростью, большей скорости первого автомобилиста на 21 км/ч, в результате чего прибыл в В одновременно первым автомобилистом. Найдите скорость первого автомобилиста.

(352425) Из А и В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал половину пути со скоростью 57 км/ч, а вторую половину пути проехал со скоростью, большей скорости первого автомобилиста на 38 км/ч, в результате чего прибыл в В одновременно первым автомобилистом. Найдите скорость первого автомобилиста.

(348780) Из А и В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал половину пути со скоростью 42 км/ч, а вторую половину пути проехал со скоростью, большей скорости первого автомобилиста на 8 км/ч, в результате чего прибыл в В одновременно первым автомобилистом. Найдите скорость первого автомобилиста.

(348809) Из А и В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал половину пути со скоростью 36 км/ч, а вторую половину пути проехал со скоростью, большей скорости первого автомобилиста на 15 км/ч, в результате чего прибыл в В одновременно первым автомобилистом. Найдите скорость первого автомобилиста.

(348824) Из А и В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал половину пути со скоростью 33 км/ч, а вторую половину пути проехал со скоростью, большей скорости первого автомобилиста на 22 км/ч, в результате чего прибыл в В одновременно первым автомобилистом. Найдите скорость первого автомобилиста.

(350863) Из А и В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал половину пути со скоростью 48 км/ч, а вторую половину пути проехал со скоростью, большей скорости первого автомобилиста на 32 км/ч, в результате чего прибыл в В одновременно первым автомобилистом. Найдите скорость первого автомобилиста.

(338669) Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в В на 48 минут раньше, чем велосипедист приехал в А, а встретились они через 18 минут после выезда. Сколько часов затратил на путь из В в А велосипедист?

(338691) Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в В на 56 минут раньше, чем велосипедист приехал в А, а встретились они через 21 минуту после выезда. Сколько часов затратил на путь из В в А велосипедист?

(338716) Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в В на 30 минут раньше, чем велосипедист приехал в А, а встретились они через 20 минут после выезда. Сколько часов затратил на путь из В в А велосипедист?

(338928) Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в В на 42 минут раньше, чем велосипедист приехал в А, а встретились они через 28 минут после выезда. Сколько часов затратил на путь из В в А велосипедист?

(352780) Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в В на 33 минут раньше, чем велосипедист приехал в А, а встретились они через 22 минуты после выезда. Сколько часов затратил на путь из В в А велосипедист?

(348376) Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в В на 39 минут раньше, чем велосипедист приехал в А, а встретились они через 26 минут после выезда. Сколько часов затратил на путь из В в А велосипедист?

(350941) Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в В на 45 минут раньше, чем велосипедист приехал в А, а встретились они через 12 минут после выезда. Сколько часов затратил на путь из В в А велосипедист?

(352737) Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в В на 36 минут раньше, чем велосипедист приехал в А, а встретились они через 24 минут после выезда. Сколько часов затратил на путь из В в А велосипедист?

(338919, 341056) Первые 300 км автомобиль ехал со скоростью 60 км/ч, следующие 300 км – со скоростью 100 км/ч, а последние 300 км – со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

(348590) Первые 350 км автомобиль ехал со скоростью 70 км/ч, следующие 105 км – со скоростью 35 км/ч, а последние 160 км – со скоростью 80 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

(348789) Первые 330 км автомобиль ехал со скоростью 110 км/ч, следующие 105 км – со скоростью 35 км/ч, а последние 150 км – со скоростью 50 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

(349420) Первые 140 км автомобиль ехал со скоростью 70 км/ч, следующие 195 км – со скоростью 65 км/ч, а последние 225 км – со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

(351253) Первые 345 км автомобиль ехал со скоростью 115 км/ч, следующие 130 км – со скоростью 65 км/ч, а последние 380 км – со скоростью 95 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

(351277) Первые 105 км автомобиль ехал со скоростью 35 км/ч, следующие 120 км – со скоростью 60 км/ч, а последние 500 км – со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

(351350) Первые 550 км автомобиль ехал со скоростью 110 км/ч, следующие 150 км – со скоростью 50 км/ч, а последние 180 км – со скоростью 60 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

(351532) Первые 160 км автомобиль ехал со скоростью 80 км/ч, следующие 100 км – со скоростью 50 км/ч, а последние 360 км – со скоростью 90 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

(351597) Первые 500 км автомобиль ехал со скоростью 100 км/ч, следующие 225 км – со скоростью 75 км/ч, а последние 100 км – со скоростью 50 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

(351645) Первые 140 км автомобиль ехал со скоростью 70 км/ч, следующие 180 км – со скоростью 60 км/ч, а последние 225 км – со скоростью 45 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

(351752) Первые 90 км автомобиль ехал со скоростью 45 км/ч, следующие 400 км – со скоростью 100 км/ч, а последние 150 км – со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

(352009) Первые 450 км автомобиль ехал со скоростью 90 км/ч, следующие 230 км – со скоростью 115 км/ч, а последние 120 км – со скоростью 40 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

(352073) Первые 300 км автомобиль ехал со скоростью 100 км/ч, следующие 380 км – со скоростью 95 км/ч, а последние 150 км – со скоростью 50 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

(352438) Первые 200 км автомобиль ехал со скоростью 50 км/ч, следующие 320 км – со скоростью 80 км/ч, а последние 140 км – со скоростью 35 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

(352576) Первые 90 км автомобиль ехал со скоростью 45 км/ч, следующие 70 км – со скоростью 35 км/ч, а последние 420 км – со скоростью 105 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

(352756) Первые 200 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км – со скоростью 90 км/ч, а последние 180 км – со скоростью 45 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

(353200) Первые 500 км автомобиль ехал со скоростью 100 км/ч, следующие 100 км – со скоростью 50 км/ч, а последние 165 км – со скоростью 55 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

(353245) Первые 425 км автомобиль ехал со скоростью 85 км/ч, следующие 325 км – со скоростью 65 км/ч, а последние 300 км – со скоростью 60 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

(338961) Первую половину трассы автомобиль проехал со скоростью 55 км/ч, вторую – со скоростью 70 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

(341393) Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 3 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 9 минут назад. Найдите скорость первого бегуна, если известно, что она на 6 км/ч меньше скорости второго.

(353530) Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 1 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 15 минут назад. Найдите скорость первого бегуна, если известно, что она на 6 км/ч меньше скорости второго.

(348444) Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 4 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 20 минут назад. Найдите скорость первого бегуна, если известно, что она на 11 км/ч меньше скорости второго.

(348497) Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 1 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 20 минут назад. Найдите скорость первого бегуна, если известно, что она на 7 км/ч меньше скорости второго.

(348811) Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 5 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 6 минут назад. Найдите скорость первого бегуна, если известно, что она на 7 км/ч меньше скорости второго.

(349197) Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 2 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 24 минут назад. Найдите скорость первого бегуна, если известно, что она на 10 км/ч меньше скорости второго.

(349342) Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 3 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 9 минут назад. Найдите скорость первого бегуна, если известно, что она на 6 км/ч меньше скорости второго.

(349536) Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 8 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 3 минуты назад. Найдите скорость первого бегуна, если известно, что она на 9 км/ч меньше скорости второго.

(349823) Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 1 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 15 минут назад. Найдите скорость первого бегуна, если известно, что она на 5 км/ч меньше скорости второго.

(349975) Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 2 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 20 минут назад. Найдите скорость первого бегуна, если известно, что она на 9 км/ч меньше скорости второго.

(350280) Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 5 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 10 минут назад. Найдите скорость первого бегуна, если известно, что она на 8 км/ч меньше скорости второго.

(350303) Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 2 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 9 минут назад. Найдите скорость первого бегуна, если известно, что она на 5 км/ч меньше скорости второго.

(350894) Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 1 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 30 минут назад. Найдите скорость первого бегуна, если известно, что она на 12 км/ч меньше скорости второго.

(351270) Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 6 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 9 минут назад. Найдите скорость первого бегуна, если известно, что она на 9 км/ч меньше скорости второго.

(351900) Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 2 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 4 минуты назад. Найдите скорость первого бегуна, если известно, что она на 3 км/ч меньше скорости второго.

(352352) Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 3 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 6 минут назад. Найдите скорость первого бегуна, если известно, что она на 5 км/ч меньше скорости второго.

(352375) Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 7 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 3 минуты назад. Найдите скорость первого бегуна, если известно, что она на 8 км/ч меньше скорости второго.

(352392) Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 4 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 6 минут назад. Найдите скорость первого бегуна, если известно, что она на 6 км/ч меньше скорости второго.

(352495) Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 4 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 18 минут назад. Найдите скорость первого бегуна, если известно, что она на 10 км/ч меньше скорости второго.

(353134) Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 1 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 3 минуты назад. Найдите скорость первого бегуна, если известно, что она на 2 км/ч меньше скорости второго.

(352782, 350982) Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 100 км. Отдохнув, он отправился обратно в город А, увеличив скорость на 15 км/ч. По пути он сделал остановку на 6 часов, в результате чего затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В.

(348373, 351417) Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 112 км. Отдохнув, он отправился обратно в город А, увеличив скорость на 9 км/ч. По пути он сделал остановку на 4 часа, в результате чего затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В.

(348458, 352556) Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 208 км. Отдохнув, он отправился обратно в город А, увеличив скорость на 3 км/ч. По пути он сделал остановку на 3 часа, в результате чего затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В.

(348991, 350918) Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 140 км. Отдохнув, он отправился обратно в город А, увеличив скорость на 6 км/ч. По пути он сделал остановку на 3 часа, в результате чего затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В.

(349001) Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 105 км. Отдохнув, он отправился обратно в город А, увеличив скорость на 16 км/ч. По пути он сделал остановку на 4 часа, в результате чего затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В.

(349002, 349144) Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 209 км. Отдохнув, он отправился обратно в город А, увеличив скорость на 8 км/ч. По пути он сделал остановку на 8 часов, в результате чего затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В.

(349981, 352707) Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 224 км. Отдохнув, он отправился обратно в город А, увеличив скорость на 2 км/ч. По пути он сделал остановку на 2 часа, в результате чего затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В.

(350014, 352723) Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 180 км. Отдохнув, он отправился обратно в город А, увеличив скорость на 5 км/ч. По пути он сделал остановку на 3 часа, в результате чего затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В.

(350597) Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 105 км. Отдохнув, он отправился обратно в город А, увеличив скорость на 16 км/ч. По пути он сделал остановку на 4 часа, в результате чего затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В.

(351513, 351620) Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 140 км. Отдохнув, он отправился обратно в город А, увеличив скорость на 14 км/ч. По пути он сделал остановку на 5 часов, в результате чего затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В.

(352865) Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 27 км. Турист прошёл путь из А в В за 8 часов, из которых спуск занял 3 часа. С какой скоростью турист шёл на спуске, если его скорость на подъёме меньше его скорости на спуске на 1 км/ч?

(348520) Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 31 км. Турист прошёл путь из А в В за 7 часов, из которых спуск занял 5 часов. С какой скоростью турист шёл на спуске, если его скорость на подъёме меньше его скорости на спуске на 2 км/ч?

(348972) Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 9 км. Турист прошёл путь из А в В за 3 часа, из которых спуск занял 1 час. С какой скоростью турист шёл на спуске, если его скорость на подъёме меньше его скорости на спуске на 3 км/ч?

(348974) Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 14 км. Турист прошёл путь из А в В за 3 часа, из которых спуск занял 1 час. С какой скоростью турист шёл на спуске, если его скорость на подъёме меньше его скорости на спуске на 2 км/ч?

(349095) Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 22 км. Турист прошёл путь из А в В за 8 часов, из которых спуск занял 3 часа. С какой скоростью турист шёл на спуске, если его скорость на подъёме меньше его скорости на спуске на 2 км/ч?

(349164) Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 11 км. Турист прошёл путь из А в В за 3 часа, из которых спуск занял 1 час. С какой скоростью турист шёл на спуске, если его скорость на подъёме меньше его скорости на спуске на 2 км/ч?

(349379) Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 25 км. Турист прошёл путь из А в В за 7 часов, из которых спуск занял 2 часа. С какой скоростью турист шёл на спуске, если его скорость на подъёме меньше его скорости на спуске на 2 км/ч?

(349381) Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 19 км. Турист прошёл путь из А в В за 4 часа, из которых спуск занял 3 часа. С какой скоростью турист шёл на спуске, если его скорость на подъёме меньше его скорости на спуске на 1 км/ч?

(349732) Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 7 км. Турист прошёл путь из А в В за 2 часа, из которых спуск занял 1 час. С какой скоростью турист шёл на спуске, если его скорость на подъёме меньше его скорости на спуске на 3 км/ч?

(349745) Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 40 км. Турист прошёл путь из А в В за 8 часов, из которых спуск занял 4 часа. С какой скоростью турист шёл на спуске, если его скорость на подъёме меньше его скорости на спуске на 2 км/ч?

(350032) Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 22 км. Турист прошёл путь из А в В за 4 часа, из которых спуск занял 3 часа. С какой скоростью турист шёл на спуске, если его скорость на подъёме меньше его скорости на спуске на 2 км/ч?

(350073) Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 10 км. Турист прошёл путь из А в В за 4 часа, из которых спуск занял 2 часа. С какой скоростью турист шёл на спуске, если его скорость на подъёме меньше его скорости на спуске на 1 км/ч?

(350225) Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 16 км. Турист прошёл путь из А в В за 4 часа, из которых спуск занял 2 часа. С какой скоростью турист шёл на спуске, если его скорость на подъёме меньше его скорости на спуске на 2 км/ч?

(350519) Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 26 км. Турист прошёл путь из А в В за 6 часов, из которых спуск занял 4 часа. С какой скоростью турист шёл на спуске, если его скорость на подъёме меньше его скорости на спуске на 2 км/ч?

(350797) Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 15 км. Турист прошёл путь из А в В за 3 часа, из которых спуск занял 2 часа. С какой скоростью турист шёл на спуске, если его скорость на подъёме меньше его скорости на спуске на 3 км/ч?

(350805) Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 16 км. Турист прошёл путь из А в В за 7 часов, из которых спуск занял 2 часа. С какой скоростью турист шёл на спуске, если его скорость на подъёме меньше его скорости на спуске на 1 км/ч?

(351224) Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 36 км. Турист прошёл путь из А в В за 8 часов, из которых спуск занял 4 часа. С какой скоростью турист шёл на спуске, если его скорость на подъёме меньше его скорости на спуске на 1 км/ч?

(351443) Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 21 км. Турист прошёл путь из А в В за 4 часа, из которых спуск занял 3 часа. С какой скоростью турист шёл на спуске, если его скорость на подъёме меньше его скорости на спуске на 3 км/ч?

(351974) Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 19 км. Турист прошёл путь из А в В за 8 часов, из которых спуск занял 3 часа. С какой скоростью турист шёл на спуске, если его скорость на подъёме меньше его скорости на спуске на 1 км/ч?

(353535) Два человека одновременно отправляются из одного и того же места по одной дороге на прогулку до опушки леса, находящейся в 3,7 км от места отправления. Один идёт со скоростью 3,3 км/ч, а другой – со скоростью 4,1 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?

(348465) Два человека одновременно отправляются из одного и того же места по одной дороге на прогулку до опушки леса, находящейся в 2,5 км от места отправления. Один идёт со скоростью 2,7 км/ч, а другой – со скоростью 4,8 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?

(348714) Два человека одновременно отправляются из одного и того же места по одной дороге на прогулку до опушки леса, находящейся в 3,1 км от места отправления. Один идёт со скоростью 2,7 км/ч, а другой – со скоростью 3,5 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?

(349247) Два человека одновременно отправляются из одного и того же места по одной дороге на прогулку до опушки леса, находящейся в 5,4 км от места отправления. Один идёт со скоростью 2,9 км/ч, а другой – со скоростью 5,8 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?

(349361) Два человека одновременно отправляются из одного и того же места по одной дороге на прогулку до опушки леса, находящейся в 1,2 км от места отправления. Один идёт со скоростью 3 км/ч, а другой – со скоростью 5 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?

(349798) Два человека одновременно отправляются из одного и того же места по одной дороге на прогулку до опушки леса, находящейся в 4,8 км от места отправления. Один идёт со скоростью 2,5 км/ч, а другой – со скоростью 5,5 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?

(349845) Два человека одновременно отправляются из одного и того же места по одной дороге на прогулку до опушки леса, находящейся в 2 км от места отправления. Один идёт со скоростью 2,2 км/ч, а другой – со скоростью 5,8 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?

(349933) Два человека одновременно отправляются из одного и того же места по одной дороге на прогулку до опушки леса, находящейся в 3 км от места отправления. Один идёт со скоростью 2,6 км/ч, а другой – со скоростью 3,9 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?

(350476) Два человека одновременно отправляются из одного и того же места по одной дороге на прогулку до опушки леса, находящейся в 5 км от места отправления. Один идёт со скоростью 2,4 км/ч, а другой – со скоростью 5,6 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?

(350557) Два человека одновременно отправляются из одного и того же места по одной дороге на прогулку до опушки леса, находящейся в 3,4 км от места отправления. Один идёт со скоростью 3,1 км/ч, а другой – со скоростью 3,7 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?

(350820) Два человека одновременно отправляются из одного и того же места по одной дороге на прогулку до опушки леса, находящейся в 1,4 км от места отправления. Один идёт со скоростью 3,6 км/ч, а другой – со скоростью 4,8 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?

(350945) Два человека одновременно отправляются из одного и того же места по одной дороге на прогулку до опушки леса, находящейся в 3,6 км от места отправления. Один идёт со скоростью 2,7 км/ч, а другой – со скоростью 4,5 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?

(352183) Два человека одновременно отправляются из одного и того же места по одной дороге на прогулку до опушки леса, находящейся в 0,9 км от места отправления. Один идёт со скоростью 2,2 км/ч, а другой – со скоростью 4,4 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?

(352279) Два человека одновременно отправляются из одного и того же места по одной дороге на прогулку до опушки леса, находящейся в 2 км от места отправления. Один идёт со скоростью 3,8 км/ч, а другой – со скоростью 5,7 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?

(352533) Два человека одновременно отправляются из одного и того же места по одной дороге на прогулку до опушки леса, находящейся в 2,7 км от места отправления. Один идёт со скоростью 3 км/ч, а другой – со скоростью 5,1 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?

(352670) Два человека одновременно отправляются из одного и того же места по одной дороге на прогулку до опушки леса, находящейся в 3,3 км от места отправления. Один идёт со скоростью 3,2 км/ч, а другой – со скоростью 3,4 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?

(352822) Два человека одновременно отправляются из одного и того же места по одной дороге на прогулку до опушки леса, находящейся в 1,5 км от места отправления. Один идёт со скоростью 2,4 км/ч, а другой – со скоростью 5,6 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?

(352923) Два человека одновременно отправляются из одного и того же места по одной дороге на прогулку до опушки леса, находящейся в 3 км от места отправления. Один идёт со скоростью 3,4 км/ч, а другой – со скоростью 5,1 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?

(353270) Два человека одновременно отправляются из одного и того же места по одной дороге на прогулку до опушки леса, находящейся в 2,4 км от места отправления. Один идёт со скоростью 3,3 км/ч, а другой – со скоростью 3,9 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?

Источник

Тренировочная работа №5 статград по математике 9 класс пробное ОГЭ ответы и задания для вариантов: МА1990701, МА1990702, МА1990703, МА1990704. Официальная дата проведения работы: 12.05.2020 (12 мая 2020 год).

Ссылка для скачивания вариантов заданий (МА1990701-МА1990704): скачать

Ссылка для скачивания ответов и критериев для вариантов: скачать

Решать тренировочную работу №5 по математике 9 класс онлайн:

Некоторые задания и ответы с вариантов:

Гриша летом отдыхает у дедушки в деревне Ушаково. В субботу они собираются съездить на машине в село Бережки. Из Ушакова в Бережки можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Дубёнки до деревни Афонино, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Бережки. Есть и третий маршрут: в деревне Дубёнки можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в село Бережки. По шоссе Гриша с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге — 50 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 2 км.

1)Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответе запишите полученную последовательность четырёх цифр. Ответ: 2431

2)Найдите расстояние от деревни Ушаково до села Бережки по прямой. Ответ выразите в километрах. Ответ: 34

3)Сколько километров проедут Гриша с дедушкой, если они поедут по шоссе через Афонино? Ответ:46

4)Сколько времени затратят на дорогу Гриша с дедушкой, если они поедут сначала до деревни Дубёнки, а затем свернут на грунтовую дорогу, идущую мимо озера? Ответ выразите в минутах. Ответ: 42

6)Определите, на какой маршрут потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Гриша с дедушкой, если поедут этим маршрутом. Ответ: 408

7)Родительский комитет закупил 20 пазлов для подарков детям в связи с окончанием учебного года, из них 11 с машинами и 9 с видами городов. Подарки распределяются случайным образом между 20 детьми, среди которых есть Илюша. Найдите вероятность того, что Илюше достанется пазл с машиной. Ответ: 0,55

8)Выписаны первые три члена арифметической прогрессии: 10; 6; 2; … Найдите 6-й член этой прогрессии.

9)Центростремительное ускорение при движении по окружности 2в м/с вычисляется по формуле 2 ω aR = , где ω — угловая скорость ( ) 1вс − , R — радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус R, если угловая скорость равна 1 8,5с− , а центростремительное ускорение равно 2 289м/с . Ответ дайте в метрах.

10)Высота равностороннего треугольника равна 9 корень 3 . Найдите сторону этого треугольника.

11)В треугольнике ABC известно, что AC=30 ,BC =16 , угол C равен 90°. Найдите радиус описанной около этого треугольника окружности.

12)Площадь параллелограмма ABCD равна 104. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.

13)Какое из следующих утверждений верно? 1) Две различные прямые, перпендикулярные третьей прямой, параллельны. 2) Если диагонали выпуклого четырёхугольника равны и перпендикулярны, то этот четырёхугольник является квадратом. 3) Все углы ромба равны. В ответе запишите номер выбранного утверждения.

14)Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 60 км. На следующий день он отправился обратно в город А, увеличив скорость на 10 км/ч. По пути он сделал остановку на 3 часа, в результате чего затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А.

15)Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 3,6, а AB=8.

16)Основания BC и AD трапеции ABCD равны соответственно 9 и 36, BD =18 . Докажите, что треугольники CBD и BDA подобны.

17)В треугольнике ABC известны длины сторон AB= 84, AC = 98, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.

18)Найдите расстояние от деревни Осинки до села Кудрино по прямой. Ответ выразите в километрах.

19)Сколько километров проедут Гена с дедушкой, если они поедут по шоссе через деревню Кулаки?

20)Сколько времени затратят на дорогу Гена с дедушкой, если они поедут сначала до Илькина, а затем свернут на грунтовую дорогу, идущую мимо озера? Ответ выразите в минутах.

21)Определите, на какой маршрут потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Гена с дедушкой, если поедут этим маршрутом.

22)Родительский комитет закупил 25 пазлов для подарков детям в связи с окончанием учебного года, из них 21 с машинами и 4 с видами городов. Подарки распределяются случайным образом между 25 детьми, среди которых есть Саша. Найдите вероятность того, что Саше достанется пазл с машиной.

23)Выписаны первые три члена арифметической прогрессии: -9 ; -5; -1 ; … Найдите 8-й член этой прогрессии.

24)Высота равностороннего треугольника равна 8 корень 3 . Найдите сторону этого треугольника.

25)В треугольнике ABC известно, что AC = 8, BC =15, угол C равен 90° . Найдите радиус описанной около этого треугольника окружности.

26)Площадь параллелограмма ABCD равна 92.Точка E — середина стороны AB. Найдите площадь трапеции DAEC.

27)Какое из следующих утверждений верно? 1) Площадь любого параллелограмма равна произведению длин его сторон. 2) Треугольник со сторонами 1, 2, 4 существует. 3) Основания любой трапеции параллельны. В ответе запишите номер выбранного утверждения.

28)Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 112 км. На следующий день он отправился обратно в город А, увеличив скорость на 9 км/ч. По пути он сделал остановку на 4 часа, в результате чего затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В.

29)Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB = 9, AC =12 .

30)Основания BC и AD трапеции ABCD равны соответственно 5 и 45, BD =15. Докажите, что треугольники CBD и BDA подобны.

31)В треугольнике ABC известны длины сторон AB = 28 , AC = 56 , точка O — центр окружности, описанной около треугольника ABC . Прямая BD, перпендикулярная прямой AO , пересекает сторону AC в точке D . Найдите CD.

Ссылка для скачивания всех ответов и решений (с 1 по 26 задание) для 9 класса: скачать

Смотрите также:

СтатГрад

Архив работ

Источник

ПОДЕЛИТЬСЯ

Решать тренировочную работу №5 по математике 9 класс онлайн:

Ссылка для скачивания всех ответов и решений (с 1 по 26 задание) для 9 класса: скачать

Смотрите также:

Добавить комментарий Отменить ответ

ПОДЕЛИТЬСЯ

Решать тренировочную работу №5 по математике 9 класс онлайн:

Ссылка для скачивания всех ответов и решений (с 1 по 26 задание) для 9 класса: скачать

Смотрите также:

Вам также может понравиться

Superfetch ошибка как исправить

Как найти шифр на телефоне

Блины в дырочку как исправить

Добавить комментарий Отменить ответ