В данной статье рассмотрим способы определить расстояние от точки до точки теоретически и на примере конкретных задач. И для начала введем некоторые определения.
Расстояние между точками – это длина отрезка, их соединяющего, в имеющемся масштабе. Задать масштаб необходимо, чтобы иметь для измерения единицу длины. Потому в основном задача нахождения расстояния между точками решается при использовании их координат на координатной прямой, в координатной плоскости или трехмерном пространстве.
Расстояние между точками на координатной прямой
Исходные данные: координатная прямая Ox и лежащая на ней произвольная точка А. Любой точке прямой присуще одно действительное число: пусть для точки А это будет некое число хA, оно же – координата точки А.
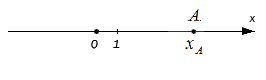
В целом можно говорить о том, что оценка длины некого отрезка происходит в сравнении с отрезком, принятым за единицу длины в заданном масштабе.
Если точке А соответствует целое действительное число, отложив последовательно от точки О до точки по прямой ОА отрезки – единицы длины, мы можем определить длину отрезка OA по итоговому количеству отложенных единичных отрезков.
К примеру, точке А соответствует число 3 – чтобы попасть в нее из точки О, необходимо будет отложить три единичных отрезка. Если точка А имеет координату -4 – единичные отрезки откладываются аналогичным образом, но в другом, отрицательном направлении. Таким образом в первом случае, расстояние ОА равно 3; во втором случае ОА = 4.
Если точка A имеет в качестве координаты рациональное число, то от начала отсчета (точка О) мы откладываем целое число единичных отрезков, а затем его необходимую часть. Но геометрически не всегда возможно произвести измерение. К примеру, затруднительным представляется отложить на координатной прямой дробь 4111.
Вышеуказанным способом отложить на прямой иррациональное число и вовсе невозможно. К примеру, когда координата точки А равна 11 . В таком случае возможно обратиться к абстракции: если заданная координата точки А больше нуля, то OA=xA (число принимается за расстояние); если координата меньше нуля, то OA=-xA . В общем, эти утверждения справедливы для любого действительного числа xA.
Резюмируя: расстояние от начала отсчета до точки, которой соответствует действительное число на координатной прямой, равно:
- 0, если точка совпадает с началом координат;
- xA , если xA>0;
- -xA , если xA<0 .
При этом очевидно, что сама длина отрезка не может быть отрицательной, поэтому, используя знак модуля, запишем расстояние от точки O до точки A с координатой xA: OA=xA
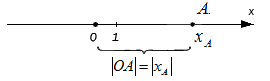
Верным будет утверждение: расстояние от одной точки до другой будет равно модулю разности координат. Т.е. для точек A и B, лежащих на одной координатной прямой при любом их расположении и имеющих соответственно координаты xA и xB : AB=xB-xA.
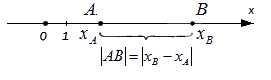
Расстояние между точками на плоскости
Исходные данные: точки A и B, лежащие на плоскости в прямоугольной системе координат Oxy с заданными координатами: A(xA, yA) и B(xB, yB) .
Проведем через точки А и B перпендикуляры к осям координат Ox и Oy и получим в результате точки проекции: Ax, Ay, Bx, By. Исходя из расположения точек А и B далее возможны следующие варианты:
– если точки А и В совпадают, то расстояние между ними равно нулю;
– если точки А и В лежат на прямой, перпендикулярной оси Ox (оси абсцисс), то точки и совпадают, а |АВ| = |АyBy|. Поскольку, расстояние между точками равно модулю разности их координат, то AyBy=yB-yA , а, следовательно AB=AyBy=yB-yA.
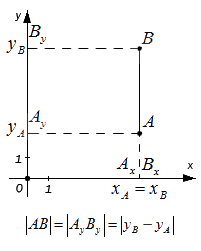
– если точки A и B лежат на прямой, перпендикулярной оси Oy (оси ординат) – по аналогии с предыдущим пунктом: AB=AxBx=xB-xA
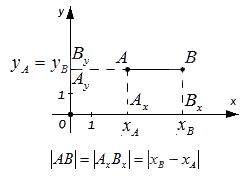
– если точки A и B не лежат на прямой, перпендикулярной одной из координатных осей, найдем расстояние между ними, выведя формулу расчета:
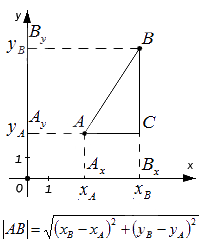
Мы видим, что треугольник АВС является прямоугольным по построению. При этом AC=AxBx и BC=AyBy. Используя теорему Пифагора, составим равенство: AB2=AC2+BC2⇔AB2=AxBx2+AyBy2 , а затем преобразуем его: AB=AxBx2+AyBy2=xB-xA2+yB-yA2=(xB-xA)2+(yB-yA)2
Сформируем вывод из полученного результата: расстояние от точки А до точки В на плоскости определяется расчётом по формуле с использованием координат этих точек
AB=(xB-xA)2+(yB-yA)2
Полученная формула также подтверждает ранее сформированные утверждения для случаев совпадения точек или ситуаций, когда точки лежат на прямых, перпендикулярных осям. Так, для случая совпадения точек A и B будет верно равенство: AB=(xB-xA)2+(yB-yA)2=02+02=0
Для ситуации, когда точки A и B лежат на прямой, перпендикулярной оси абсцисс:
AB=(xB-xA)2+(yB-yA)2=02+(yB-yA)2=yB-yA
Для случая, когда точки A и B лежат на прямой, перпендикулярной оси ординат:
AB=(xB-xA)2+(yB-yA)2=(xB-xA)2+02=xB-xA
Расстояние между точками в пространстве
Исходные данные: прямоугольная система координат Oxyz с лежащими на ней произвольными точками с заданными координатами A(xA, yA, zA) и B(xB, yB, zB) . Необходимо определить расстояние между этими точками.
Рассмотрим общий случай, когда точки A и B не лежат в плоскости, параллельной одной из координатных плоскостей. Проведем через точки A и B плоскости, перпендикулярные координатным осям, и получим соответствующие точки проекций: Ax, Ay, Az, Bx, By, Bz
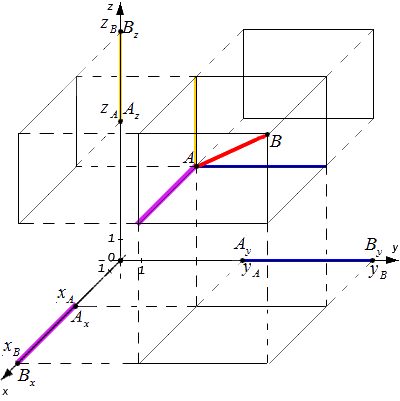
Расстояние между точками A и B являет собой диагональ полученного в результате построения параллелепипеда. Согласно построению измерения этого параллелепипеда: AxBx, AyBy и AzBz
Из курса геометрии известно, что квадрат диагонали параллелепипеда равен сумме квадратов его измерений. Исходя из этого утверждения получим равенство: AB2=AxBx2+AyBy2+AzBz2
Используя полученные ранее выводы, запишем следующее:
AxBx=xB-xA, AyBy=yB-yA, AzBz=zB-zA
Преобразуем выражение:
AB2=AxBx2+AyBy2+AzBz2=xB-xA2+yB-yA2+zB-zA2==(xB-xA)2+(yB-yA)2+zB-zA2
Итоговая формула для определения расстояния между точками в пространстве будет выглядеть следующим образом:
AB=xB-xA2+yB-yA2+(zB-zA)2
Полученная формула действительна также для случаев, когда:
– точки совпадают;
– лежат на одной координатной оси или прямой, параллельной одной из координатных осей.
Примеры решения задач на нахождение расстояния между точками
Исходные данные: задана координатная прямая и точки, лежащие на ней с заданными координатами A(1-2) и B(11+2) . Необходимо найти расстояние от точки начала отсчета O до точки A и между точками A и B.
Решение
- Расстояние от точки начала отсчета до точки равно модулю координаты этой точки, соответственно OA=1-2=2-1
- Расстояние между точками A и B определим как модуль разности координат этих точек: AB=11+2-(1-2)=10+22
Ответ: OA=2-1, AB=10+22
Исходные данные: задана прямоугольная система координат и две точки, лежащие на ней A(1, -1) и B (λ+1, 3) . λ – некоторое действительное число. Необходимо найти все значения этого числа, при которых расстояние АВ будет равно 5.
Решение
Чтобы найти расстояние между точками A и B, необходимо использовать формулу AB=(xB-xA)2+yB-yA2
Подставив реальные значения координат, получим:AB=(λ+1-1)2+(3-(-1))2=λ2+16
А также используем имеющееся условие, что АВ=5 и тогда будет верным равенство:
λ2+16=5λ2+16=25λ=±3
Ответ: АВ = 5, если λ=±3 .
Исходные данные: задано трехмерное пространство в прямоугольной системе координат Oxyz и лежащие в нем точки A (1, 2, 3) и B-7, -2, 4 .
Решение
Для решения задачи используем формулу AB=xB-xA2+yB-yA2+(zB-zA)2
Подставив реальные значения, получим: AB=(-7-1)2+(-2-2)2+(4-3)2=81=9
Ответ: |АВ| = 9
Загрузить PDF
Загрузить PDF
Расстояние (обозначим как d) – это длина прямой между двумя точками. Расстояние можно найти между двумя неподвижными точками, а можно найти расстояние, пройденное движущимся телом. В большинстве случаев расстояние может быть вычислено по следующим формулам: d = s × t, где d – расстояние, s – скорость, t – время; d = √((x2 – x1)2 + (y2 – y1)2, где (x1, y1) и (x2, y2) – координаты двух точек.
-

1
Чтобы вычислить расстояние, пройденное движущимся телом, вам необходимо знать скорость тела и время в пути, чтобы подставить их в формулу d = s × t.
- Пример. Автомобиль едет со скоростью 120 км/ч в течение 30 минут. Необходимо вычислить пройденное расстояние.
-

2
Перемножьте скорость и время и вы найдете пройденное расстояние.
- Обратите внимание на единицы измерения величин. Если они различны, вам необходимо конвертировать одну из них так, чтобы она соответствовала другой единице. В нашем примере скорость измеряется в километрах в час, а время – в минутах. Поэтому необходимо конвертировать минуты в часы; для этого значение времени в минутах необходимо разделить на 60 и вы получите значение времени в часах: 30/60 = 0,5 часов.
- В нашем примере: 120 км/ч х 0,5 ч = 60 км. Обратите внимание, что единица измерения «час» сокращается и остается единица измерения «км» (то есть расстояние).
-

3
Описанную формулу можно использовать для вычисления входящих в нее величин. Для этого обособьте нужную величину на одной стороне формулы и подставьте в нее значения двух других величин. Например, для вычисления скорости используйте формулу s = d/t, а для вычисления времени – t = d/s.
- Пример. Автомобиль проехал 60 км за 50 минут. В этом случае его скорость равна s = d/t = 60/50 = 1,2 км/мин.
- Обратите внимание, что результат измеряется в км/мин. Чтобы конвертировать эту единицу измерения в км/ч, умножьте результат на 60 и получите 72 км/ч.
-

4
Данная формула вычисляет среднюю скорость, то есть предполагается, что в течение всего времени в пути тело имеет постоянную (неизменную) скорость. Это годится в случае абстрактных задач и моделирования движения тел. В реальной жизни скорость тела может меняться, то есть тело может ускоряться, замедляться, останавливаться или двигаться в обратном направлении.
- В предыдущем примере мы нашли, что автомобиль, проехавший 60 км за 50 минут, ехал со скоростью 72 км/ч. Это справедливо только при условии, что с течением времени скорость автомобиля не менялась. Например, если в течение 25 минут (0,42 часов) автомобиль ехал со скорость 80 км/ч, а в течение еще 25 минут (0,42 часов) – со скоростью 64 км/час, он тоже проедет 60 км за 50 минут (80 х 0,42 + 64 х 0,42 = 60).
- Для решения задач, включающих меняющуюся скорость тела, лучше использовать производные, а не формулу для вычисления скорости по расстоянию и времени.
Реклама
-

1
Найдите две точки пространственных координат. Если вам даны две неподвижные точки, то, чтобы вычислить расстояние между этими точками, необходимо знать их координаты; в одномерном пространстве (на числовой прямой) вам понадобятся координаты x1 и x2, в двумерном пространстве – координаты (x1,y1) и (x2,y2), в трехмерном пространстве – координаты (x1,y1,z1) и (x2,y2,z2).
-

2
Вычислите расстояние в одномерном пространстве (точки лежат на одной горизонтальной прямой) по формуле: d = |x2 – x1|, то есть вы вычитаете «х» координаты, а затем находите модуль полученного значения.
- Обратите внимание, что в формулу включены скобки модуля (абсолютного значения). Модуль числа – это неотрицательное значение этого числа (то есть модуль отрицательного числа равен этому числу со знаком плюс).
- Пример. Машина находится между двумя городами. До города, который находится перед ней, 5 км, а до города за ней – 1 км. Вычислите расстояние между городами. Если взять машину за точку отсчета (за 0), то координата первого города x1 = 5, а второго x2 = -1. Расстояние между городами:
- d = |x2 – x1|
- = |-1 – 5|
- = |-6| = 6 км.
-

3
Вычислите расстояние в двумерном пространстве по формуле: d = √((x2 – x1)2 + (y2 – y1)2). То есть вы вычитаете «х» координаты, вычитаете «у» координаты, возводите полученные значения в квадрат, складываете квадраты, а затем из полученного значения извлекаете квадратный корень.
- Формула для вычисления расстояния в двумерном пространстве основана на теореме Пифагора, которая гласит, что гипотенуза прямоугольного треугольника равна квадратному корню из суммы квадратов обоих катетов.
- Пример. Найдите расстояние между двумя точками с координатами (3, -10) и (11, 7) (центр окружности и точка на окружности, соответственно).
- d = √((x2 – x1)2 + (y2 – y1)2)
- d = √((11 – 3)2 + (7 – -10)2)
- d = √(64 + 289)
- d = √(353) = 18,79
-

4
Вычислите расстояние в трехмерном пространстве по формуле: d = √((x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2). Эта формула является видоизмененной формулой для вычисления расстояния в двумерном пространстве с добавлением третьей координаты «z».
- Пример. Космонавт находится в открытом космосе недалеко от двух астероидов. Первый из них расположен в 8 километрах перед космонавтом, в 2 км справа от него и в 5 км ниже него; второй астероид находится в 3 км позади космонавта, в 3 км слева от него, и в 4 км выше него. Таким образом, координаты астероидов (8,2,-5) и (-3,-3,4). Расстояние между астероидами вычисляется следующим образом:
- d = √((-3 – 8)2 + (-3 – 2)2 + (4 – -5)2)
- d = √((-11)2 + (-5)2 + (9)2)
- d = √(121 + 25 + 81)
- d = √(227) = 15,07 км
Реклама
Похожие статьи
Об этой статье
Эту страницу просматривали 61 187 раз.
Была ли эта статья полезной?
Расстояние между двумя точками, формула
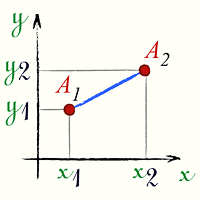
Расстояние между двумя точками
Расстояние между двумя точками A1(x1;y1) и
A2(x2;y2)
в прямоугольной системе координат выражается формулой:
[ d = sqrt{(x_2-x_1)^{2} + (y_2-y_1)^{2}} ]
Порядок точек не играет роли. Расстояние считается положительным. поэтому корень берется с одним знаком (плюс).
Вычислить, найти расстояние между двумя точками по формуле (1)
| x1 | y1 |
| x2 | y2 |
Вычислить
нажмите кнопку для расчета
Расстояние между двумя точками |
стр. 138 |
|---|
Download Article
Download Article
Distance, often assigned the variable d, is a measure of the space contained by a straight line between two points.[1]
Distance can refer to the space between two stationary points (for instance, a person’s height is the distance from the bottom of his or her feet to the top of his or her head) or can refer to the space between the current position of a moving object and its starting location. Most distance problems can be solved with the equations d = savg × t where d is distance, savg is average speed, and t is time, or using d = √((x2 – x1)2 + (y2 – y1)2), where (x1, y1) and (x2, y2) are the x and y coordinates of two points.
-

1
Find values for average speed and time. When you try to find the distance a moving object has traveled, two pieces of information are vital for making this calculation: its speed (or velocity magnitude) and the time that it has been moving.[2]
With this information, it’s possible to find the distance the object has traveled using the formula d = savg × t.- To better understand the process of using the distance formula, let’s solve an example problem in this section. Let’s say that we’re barreling down the road at 120 miles per hour (about 193 km per hour) and we want to know how far we will travel in half an hour. Using 120 mph as our value for average speed and 0.5 hours as our value for time, we’ll solve this problem in the next step.
-

2
Multiply average speed by time. Once you know the average speed of a moving object and the time it’s been traveling, finding the distance it has traveled is relatively straightforward. Simply multiply these two quantities to find your answer.[3]
- Note, however, that if the units of time used in your average speed value are different than those used in your time value, you’ll need to convert one or the other so that they are compatible. For instance, if we have an average speed value that’s measured in km per hour and a time value that’s measured in minutes, you would need to divide the time value by 60 to convert it to hours.
- Let’s solve our example problem. 120 miles/hour × 0.5 hours = 60 miles. Note that the units in the time value (hours) cancel with the units in the denominator of the average speed (hours) to leave only distance units (miles).
Advertisement
-

3
Manipulate the equation to solve for other variables. The simplicity of the basic distance equation (d = savg × t) makes it quite easy to use the equation for finding the values of variables besides distance. Simply isolate the variable you want to solve for according to the basic rules of algebra, then insert values for your other two variables to find the value for the third. In other words, to find your object’s average speed, use the equation savg = d/t and to find to find the time an object has been traveling, use the equation t = d/savg.
- For instance, let’s say that we know that a car has driven 60 miles in 50 minutes, but we don’t have a value for the average speed while traveling. In this case, we might isolate the savg variable in the basic distance equation to get savg = d/t, then simply divide 60 miles / 50 minutes to get an answer of 1.2 miles/minute.
- Note that in our example, our answer for speed has an uncommon units (miles/minute). To get your answer in the more common form of miles/hour, multiply it by 60 minutes/hour to get 72 miles/hour.
-

4
Note that the “savg” variable in the distance formula refers to average speed. It’s important to understand that the basic distance formula offers a simplified view of the movement of an object. The distance formula assumes that the moving object has constant speed — in other words, it assumes that the object in motion is moving at a single, unchanging rate of speed. For abstract math problems, such as the ones you may encounter in an academic setting, sometimes it’s still possible to model an object’s motion using this assumption. In real life, however, this model often doesn’t accurately reflect the motion of moving objects, which can, in reality, speed up, slow down, stop, and reverse over time.
- For instance, in the example problem above, we concluded that to travel 60 miles in 50 minutes, we’d need to travel at 72 miles/hour. However, this is only true if travel at one speed for the entire trip. For instance, by traveling at 80 miles/hr for half of the trip and 64 miles/hour for the other half, we will still travel 60 miles in 50 minutes — 72 miles/hour = 60 miles/50 min = ?????
- Calculus-based solutions using derivatives are often a better choice than the distance formula for defining an object’s speed in real-world situations because changes in speed are likely.
Advertisement
-

1
Find two points spatial coordinates. What if, rather than finding the distance that a moving object has traveled, you need to find the distance between two stationary objects? In cases like this, the speed-based distance formula described above won’t be of any use. Luckily, a separate distance formula[4]
can be used to easily find the straight-line distance between two points. However, to use this formula, you’ll need to know the coordinates of your two points. If you’re dealing with one-dimensional distance (such as on a number line), your coordinates will be two numbers, x1 and x2. If you’re dealing with distance in two dimensions, you’ll need values for two (x,y) points, (x1,y1) and (x2,y2). Finally, for three dimensions, you’ll need values for (x1,y1,z1) and (x2,y2,z2). -

2
Find 1-D distance by subtracting the value of the coordinates for the two points. Calculating one-dimensional distance between two points when you know the value for each is a cinch. Simply use the formula d = |x2 – x1|. In this formula, you subtract x1 from x2, then take the absolute value of your answer to find the distance between x1 and x2. Typically, you’ll want to use the one-dimensional distance formula when your two points lie on a number line or axis.[5]
- Note that this formula uses absolute values (the “| |” symbols). Absolute values simply mean that the terms contained within the symbols become positive if they are negative.
- For example, let’s say that we’re stopped by the side of the road on a perfectly straight stretch of highway. If there is a small town 5 miles ahead of us and a town 1 mile behind us, how far apart are the two towns? If we set town 1 as x1 = 5 and town 2 as x1 = -1, we can find d, the distance between the two towns, as follows:
- d = |x2 – x1|
- = |-1 – 5|
- = |-6| = 6 miles.
-

3
Find 2-D distance by using the Pythagorean theorem.[6]
Finding distance between two points in two-dimensional space is more complicated than in one dimension, but is not difficult. Simply use the formula d = √((x2 – x1)2 + (y2 – y1)2). In this formula, you subtract the two x coordinates, square the result, subtract the y coordinates, square the result, then add the two intermediate results together and take the square root to find the distance between your two points. This formula works in the two-dimensional plane — for example, on basic x/y graphs.[7]
- The 2-D distance formula takes advantage of the Pythagorean theorem, which dictates that the hypotenuse of a right triangle is equal to the square root of the squares of the other two sides.
- For example, let’s say that we have two points in the x-y plane: (3, -10) and (11, 7) that represent the center of a circle and a point on the circle, respectively. To find the straight-line distance between these two points, we can solve as follows:
- d = √((x2 – x1)2 + (y2 – y1)2)
- d = √((11 – 3)2 + (7 – -10)2)
- d = √(64 + 289)
- d = √(353) = 18.79
-

4
Find 3-D distance by modifying the 2-D formula. In three dimensions, points have a z coordinate in addition to their x and y coordinates. To find the distance between two points in three-dimensional space, use d = √((x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2). This is a modified form of the two-dimensional distance formula described above that takes the z coordinates into account. Subtracting the two z coordinates, squaring them, and proceeding through the rest of the formula as above will ensure your final answer represents the three-dimensional distance between your two points.[8]
- For example, let’s say that we’re an astronaut floating in space near two asteroids. One is about 8 kilometers in front of us, 2 km to the right of us, and 5 miles below us, while the other is 3 km behind us, 3 km to the left of us, and 4 km above us. If we represent the positions of these asteroids with the coordinates (8,2,-5) and (-3,-3,4), we can find the distance between the two as follows:
- d = √((-3 – 8)2 + (-3 – 2)2 + (4 – -5)2)
- d = √((-11)2 + (-5)2 + (9)2)
- d = √(121 + 25 + 81)
- d = √(227) = 15.07 km
Advertisement
Add New Question
-
Question
What is the formula for finding the distance traveled of a moving object?

Distance traveled = rate (velocity) multiplied by time elapsed. D = (v)(t).
-
Question
How do I calculate distance on a map?

Maps typically have a scale of miles. Compare a distance shown on a map with its scale.
-
Question
How do I calculate the distance traveled by a courier service truck on 20 trips?

Add together the distance traveled on each of the 20 trips. If all the trips are the same, just multiply the distance of one trip by 20.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
Thanks for submitting a tip for review!
References
About This Article
Article SummaryX
To calculate distance, start by finding the average speed the object traveled and the amount of time it was traveling for. Make sure you’re using the same units for the average speed and time or else your calculation won’t be accurate. For example, if you’re using miles per hour for the speed, you would need to use hours, not minutes or seconds, for the time. Once you have your 2 values, just multiply them together to get the distance the object traveled. To learn how to calculate the distance between 2 points, scroll down!
Did this summary help you?
Thanks to all authors for creating a page that has been read 257,648 times.
Did this article help you?
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,657 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,952 -
разное
16,904
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
