Как найти расстояние после неупругого удара

Закон сохранения механической энергии и закон сохранения импульса при упругом ударе способствует нахождению решения механических задач с неизвестными действующими силами, то есть задания с ударным взаимодействием тел.

Применение такого вида задач используется в технике и физике элементарных частиц.

Удар или столкновение – это кратковременное взаимодействие тел с последующим изменением их скорости.

При столкновении действуют неизвестные кратковременные ударные силы. Закон Ньютона не разрешит ударное взаимодействие, а позволит только исключить сам процесс столкновения и получить связь между скоростями тел до и после столкновений без промежуточных значений.

Механика применяет такое определения абсолютно упругих и абсолютно неупругих ударов.

Абсолютно неупругий удар. Скорость

Абсолютно неупругий удар – это ударное взаимодействие с соединением (слипанием) движущихся тел.

Сохранение механической энергии отсутствует, так как переходит во внутреннюю, то есть нагревание.

Попадание пули в баллистический маятник – характерный пример действия энергии абсолютно неупругого удара, где
М – подвешенный ящик с песком, показанный на рисунке 1.21.1, m – горизонтально летящая пуля с v→ скоростью движения, застревающая в ящике. Определение скорости пули возможно по отклонению маятника.

Если скорость ящика с пулей обозначить как u→, тогда, используя формулу сохранения импульса, получаем:

mv=(M+m)u; u=mM+mv.

Когда пуля застревает в песке, то механическая энергия теряется:

∆E=mv22-(M+m)u22=MM+m·mv22.

M (M + m) обозначает долю кинетической энергии выпущенной пули и прошедшей во внутреннюю энергию системы. Тогда

∆EE0=MM+m=11+mM.

Использование формулы подходит для задач с наличием баллистического маятника и другого неупругого соударения разномасных тел.

Когда m << М ∆EE0→12, тогда происходит переход кинетической энергии во внутреннюю. Когда m = M ∆EE0→0, только половина кинетической переходит во внутреннюю. Если имеется неупругое соударение движущегося тела большей массой с неподвижным, имеющим (m>>М), отношение принимает вид ∆EE0→0.

Расчет движения маятника производится по закону сохранения механической энергии. Получаем

(M+m)u22=(M+m)gh; u2=2gh.

В данном случае h является максимальной высотой подъема маятника. Отсюда следует, что

v=M+mm2gh.

При известной высоте h возможно определение скорости пули v.

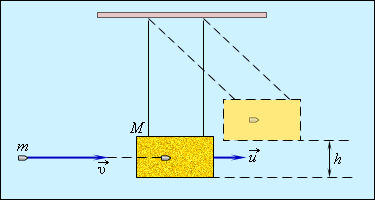
Рисунок 1.21.1. Баллистический маятник.

Абсолютно упругий удар

Абсолютный упругий удар – это столкновение с сохранением механической энергии системы тел.

Большинство случаев столкновения атомов подчинено законам абсолютного упругого центрального удара. Закон сохранения импульса и механической энергии сохраняются при таком ударе. Для примера используется столкновение при помощи центрального удара бильярдных шаров. Один из них находится в состоянии покоя, как изображено подробно на рисунке 1.21.2.

Центральный удар – это соударение, когда скорости шаров направлены по линии центра.

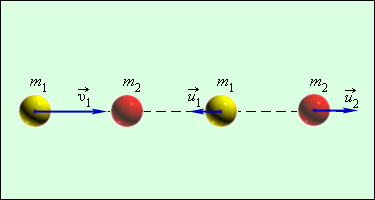
Рисунок 1.21.2. Абсолютно упругий центральный удар шаров.

Встречаются случаи, когда массы m1 и m2 не равны. Тогда, используя закон сохранения механической энергии, получаем

m1v122=m1v122+m2v222.

За v1 принимается скорость при абсолютном упругом ударе первого шара перед столкновением, а v2=0 скорость второго шара, u1 и u2 – скорости после столкновения.

Полученная система из двух уравнений позволяет найти неизвестные скорости u1 и u2 шаров после столкновения.

u1=m1-m2v1m1+m2; u2=2m1v1m1+m2.

Если массы равны, то есть, тогда происходит остановка первого шара (u1=0), а второй продолжает движение u2=v1_. происходит обмен скоростями и импульсами.

При наличии нулевой скорости второго шара (v2≠0), задача могла бы свестись к предыдущей с переходим в новую систему отсчета с равномерным и прямолинейным движением и скоростью v2 относительно «неподвижной» системы. В такой системе второй шар покоится до удара, а первый имеет скорость v1’=v1–v2_. После определения скорости шаров v1 и v2 производится переход к «неподвижной» системе.

С помощью закона сохранения механической энергии и импульса, можно определить скорости шаров после столкновений только с известными скоростями до соударения.

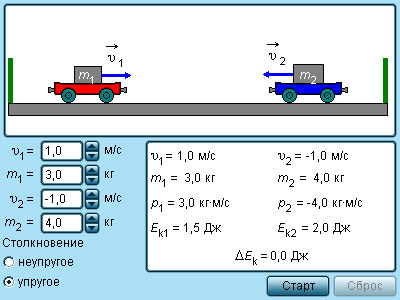
Рисунок 1.21.3. Модель упругие и неупругие соударения.

При столкновении атомов или молекул применяется понятие центрального или лобового удара, который редко применим на практике. Нецентральный упругий удар не направлен по одной прямой.

Частный случай нецентрального упругого удара – соударение бильярдных шаров с одинаковой массой при обездвиженном одним из них, а другим направленным не по линии центра. Данная ситуация приведена на рисунке 1.21.4.

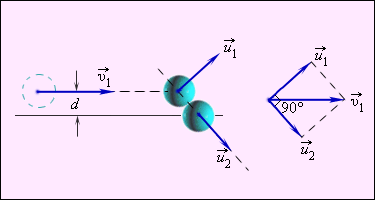
Рисунок 1.21.4. Нецентральное упругое соударение шаров с одинаковой массой, где d является прицельным расстоянием.

Нецентральное ударение характеризуется тем, что разлетатание шаров происходит под углом относительно друг друга. Чтобы определить скорости v1 и v2 после соударения, необходимо знать нахождение положения линии центров в момент удара или предельное расстояние d, изображенное на рисунке 1.21.4.

Предельное расстояние

Предельным расстоянием называют расстояние между двумя линиями, которые проведены через центры шаров параллельно относительно вектора скорости v1→ летящего шара.

При одинаковых массах шаров векторы v1→ и v2→ имеют перпендикулярное направление друг к другу. Это возможно показать с помощью применения законов сохранения импульса и энергии. Если m1=m2=m, тогда определение примет вид

v1→=u1→+u2→; v12=u12+u22.

Первое равенство значит, что векторы v1→, u1→, u2→ образуют треугольник, называемый диаграммой импульсов, второе – для его разрешения применяют теорему Пифагора. Угол, располагаемый между u1→ и u2→, равняется 90 градусов.

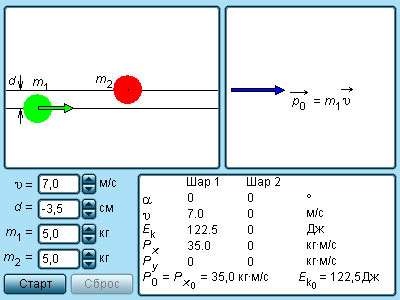
Рисунок 1.21.5. Модель соударения упругих шаров

По специальной договоренности с редколлегией и редакцией журнала «Квант»

Довольно часто на вступительных экзаменах абитуриентам предлагаются задачи, в которых рассматривается столкновение тел (иногда столкновение называют ударом, или соударением, или рассеиванием). Обычно речь идет о соударении двух тел; если же соударяющихся тел больше, их взаимодействие можно представить как совокупность попарных соударений.

Прежде чем решать любую задачу по физике, и в частности задачу на соударение, нужно понять, какие явления, рассматриваемые в задаче, играют главную роль, а какими явлениями можно пренебречь. В соответствии с этим нужно выбрать идеализированную картину и установить для нее применимость соответствующих физических законов.

Процесс столкновения тел можно разделить на три стадии: первая стадия — тела налетают друг на друга с постоянными скоростями и в какой-то момент соприкасаются друг с другом; вторая стадия (собственно соударение) — появляются силы взаимодействия между телами, которые действуют в течение некоторого промежутка времени; третья стадия — тела разлетаются с новыми неизменными во времени скоростями. Обычно формулировка задачи на соударение предполагает по заданным начальным скоростям тел определить их конечные скорости (или наоборот). При этом стадия собственно соударения фактически не рассматривается, а обсуждается лишь ее характер: удар упругий или неупругий, центральный или нецентральный и т. д.

В качестве примера рассмотрим упругий удар. Пусть небольшое тело произвольной формы налетает на другое тело. Придя в соприкосновение, тела начинают деформироваться. Возникающие упругие деформации передаются от одних частей тел к другим со скоростью распространения звука (то есть достаточно быстро), причем различные части тел получают различные скорости. Наконец, импульсы деформации достигают противоположных границ тел, отражаются от них, и тела отскакивают друг от друга подобно сжатым пружинам. Что же при этом происходит с первоначальным запасом механической энергии тел?

Из-за неодинаковости скоростей движения различных частей тел возникают колебания, они отбирают определенную энергию, которая при затухании колебаний превращается в тепло. Кроме того, всякое колеблющееся тело становится источником звуковых волн, которые тоже уносят часть энергии. Если удар нецентральный, то есть если относительная скорость соударяющихся тел не проходит по линии центров тел, тела начнут вращаться. Энергия, необходимая для этого, черпается тоже из кинетической энергии поступательного движения тел. Вращение могут вызвать также силы трения. Однако, если отношение потерь к первоначальному запасу механической энергии мало, всеми необратимыми превращениями механической энергии в другие виды энергии пренебрегают и удар считают абсолютно упругим. Идеализированная картина такого удара состоит в следующем: кинетическая энергия поступательного движения налетающих тел частично переходит в потенциальную энергию упругих деформаций; потенциальная энергия растет до тех пор, пока не сравняются скорости движения обоих тел, а затем она переходит в кинетическую энергию разлетающихся тел. Таким образом, при абсолютно упругом ударе общая механическая энергия тел сохраняется.

Заметим, что при неупругом ударе в телах возникают неупругие деформации, которые частично сохраняются и после соударения тел. При этом внутренняя энергия тел изменяется, а значит, их полная механическая энергия не сохраняется.

Теперь перейдем к рассмотрению конкретных задач. Решая их, мы не будем каждый раз детально обсуждать все происходящее. Надеемся, что читатель сумеет самостоятельно сделать подробный анализ и обосновать выбранную модель явления.

Задача 1. Два шара одинаковых радиусов движутся по гладкой, горизонтальной поверхности (рис. 1). Массы шаров m₁ и m₂, их скорост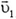и  и 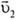 направлены по линии центров шаров. Определите скорости шаров после их абсолютно упругого удара.

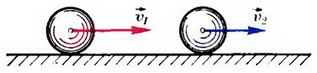
Рис. 1.

Поскольку удар абсолютно упругий и горизонтальная поверхность гладкая, импульс и кинетическая энергия системы сохраняются. До удара оба шара двигались по линии, соединяющей их центры; следовательно, удар центральный и после него шары тоже движутся вдоль линии центров. Направим ось координат по этой линии, спроектируем на нее все скорости и запишем законы сохранения импульса и кинетической энергии:

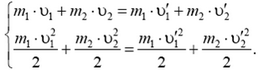
Здесь 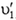 и 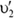 проекции новых скоростей первого и второго шаров соответственно.

Для решения полученной системы в каждом уравнении в левой части, соберем слагаемые, содержащие m₁, а в правой — слагаемые, содержащие m₂:

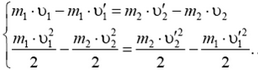
Поделив почленно второе уравнение на первое, получим

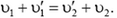
Объединим это уравнение с первым уравнением предыдущей системы в новую систему:

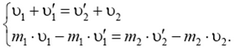
Отсюда

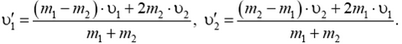
Анализируя выражения для 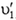 и 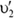, можно сделать следующие выводы:

1) При столкновениях тел одинаковых масс (m₁ = m₂)

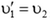 и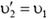

— тела обмениваются скоростями.

2) При соударении легкого и тяжелого тел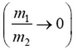

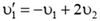 и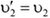

— тяжелое тело не изменяет своей скорости.

3) Если в исходной системе уравнений сделать замену 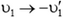 и 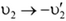, то новые скорости тел будут таким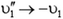и:  и 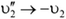. Физически это означает обратимость механического движения: если тела налетают друг на друга со скоростями, обратными тем, с которыми они двигались после удара в задаче 1, то разлетаться после удара тела будут, со скоростями, обратными тем, с которыми они двигались до удара в задаче 1.

4) 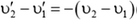 — при ударе модуль относительной скорости тел не изменяется, а направление этой скорости меняется на противоположное.

Задача 2. Небольшой шарик лежит на дне ящика, касаясь его правой стенки. В результате толчка извне ящик начинает двигаться вправо по гладкой горизонтальной поверхности со скоростью . Через какое время τ шарик займет первоначальное относительно ящика положение, если его соударения с ящиком абсолютно упругие, дно ящика гладкое, а расстояние между его стенками равно L?

Шарик будет попадать в первоначальное относительно ящика положение перед каждым четным соударением с ящиком. Поскольку модуль скорости шарика относительно ящика при ударе не меняется и все время равен υ, время τ найдем по формуле

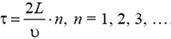
Задача 3. Гладкая вертикальная стенка движется в горизонтальном направлении со скоростью  (рис. 2). В стенку попадает шарик массой m, летящий со скоростью , которая составляет угол α с перпендикуляром к стенке. Считая удар абсолютно упругим, определите модуль υ‘ скорости шарика после удара и угол β, под которым шарик отлетит от стенки.

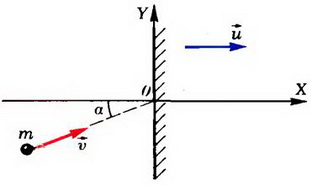
Рис. 2.

Введем систему координат XOY, как показано на рисунке 2. Обозначим через М массу стенки, через υ и и — модули скоростей шарика и стенки до соударения, через и’ — модуль скорости стенки после соударения, а через υ‘_x и υ‘_y — соответствующие проекции скорости шарика после удара. Запишем законы сохранения импульса и кинетической энергии:

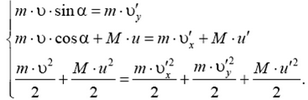
Из этой системы найдем

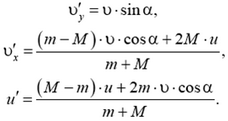
Очевидно, что масса шарика мала по сравнению с массой стенки, то есть 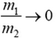. С учетом этого получим

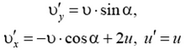
(сравните последние два выражения с выводом 2 из задачи 1). Отсюда

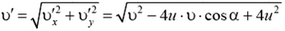
и

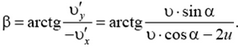
Задача 4. Пробирка массой M содержит моль идеального газа массой m при температуре m. Пробирку открывают, вынимая из нее пробку пренебрежимо малой массы. Оцените скорость пробирки после того, как весь газ выйдет из нее. Влияние окружающего воздуха можно не учитывать.

Направим ось X вдоль оси пробирки (рис. 3).

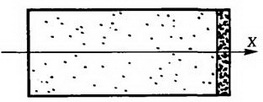
Рис. 3.

Половина общего числа молекул газа имеют проекцию скорости υ_x > 0. Эти молекулы уйдут из пробирки, не передав ей никакого импульса. Другая половина молекул передаст задней стенке пробирки свой двойной импульс, а затем также покинет пробирку. Следовательно, пробирка получит импульс (в проекции на ось X)

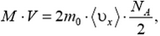
где V — проекция скорости пробирки, m₀ масса молекулы газа, 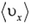 — средняя квадратическая проекция ее скорости и N_A — число Авогадро.

Учитывая, что 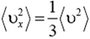, то есть средний квадрат проекции скорости равен 1/3 среднего квадрата самой скорости, и что  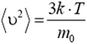(k — постоянная Больцмана), получим

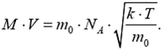
Отсюда

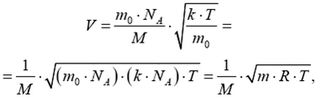
где R — универсальная газовая постоянная.

Задача 5. Гладкий неупругий шарик (из мягкого свинца) налетает на такой же шарик, находящийся в покое (рис. 4). Скорость первого шарика направлена под углом α к линии центров. Под каким углом β разлетаются шарики после удара?

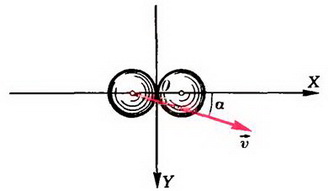
Рис. 4.

В отличие от предыдущих задач, в этой задаче рассматривается неупругое соударение. Поскольку удар неупругий, кинетическая энергия системы не сохраняется (часть ее превращается во внутреннюю). Для решения задачи воспользуемся законом сохранения импульса.

Вследствие гладкости шариков силы их взаимодействия направлены по линии центров (по оси X) и не имеют проекций на перпендикулярное направление, то есть на ось Y. Следовательно,

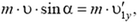
где m масса каждого шарика, υ — модуль скорости первого шарика до удара, а 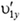 — проекция на ось Y скорости этого шарика после удара .

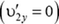Действие же сил взаимодействия между шариками при их неупругом соударении приводит к выравниванию проекций скоростей шариков на ось X. Тогда

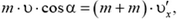
где 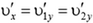 — соответствующая проекция скоростей обоих шариков после соударения.

Из полученных уравнений можно найт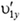и  и 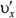, а значит и tg β:

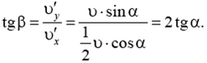
Отсюда

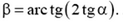
Задача 6. Ядро массой m, летящее со скоростью , распадается на два одинаковых осколка. Внутренняя энергия ядра Е₁, внутренняя энергия каждого из осколков Е₂ (E₁ > 2E₂). Определите максимально возможный угол между векторами скоростей осколков.

Процесс распада ядра на два осколка представляет собой как бы обращенный во времени процесс неупругого столкновения. Сначала оба осколка летят вместе, образуя единую систему (первая стадия). В результате действия внутренних сил система распадается на две части (вторая стадия). Осколки, образованные в результате разрыва ядра, разлетаются в разные стороны с постоянными скоростями (третья стадия).

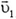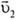Обозначим через  и  скорости осколков ядра и запишем законы сохранения импульса и полной энергии системы:

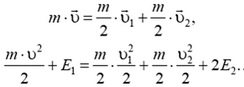
Изобразим графически скорости ядра и его осколков (рис. 5).

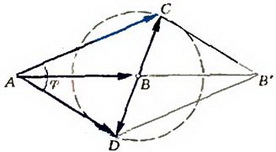
Рис. 5.

В параллелограмме ACB’D 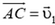 — вектор скорости первого осколка,  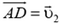— вектор скорости второго осколка и  — вектор скорости ядра до разрыва 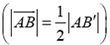. Введем дополнительные векторы  и  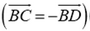 и обозначим 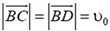. Закон сохранения полной энергии и теорема о том, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон, приводят к соотношениям

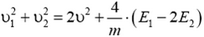
и

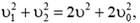
откуда

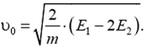
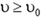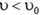Очевидно, возможны два случая: a) ; б) . Рассмотрим сначала случай а), которому как раз и соответствует рисунок 5, и найдем максимально возможный угол φ.

Для этого воспользуемся теоремой косинусов для треугольников ACD, ABD и АСВ и получим

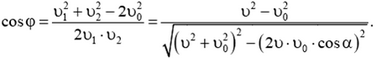
Отсюда

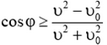
и

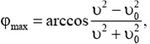
где 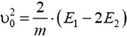. При этом .

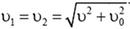Случай б) рассмотрите самостоятельно и убедитесь в том, что φ_max = π.

Упражнения

I. На пути тела массой m, скользящего по гладкому столу со скоростью , находится и неподвижная незакрепленная горка массой М и высотой H (профиль горки изображен на рисунке 6). Определите скорости тела и горки после того, как тело покинет горку. Тело движется, не отрываясь от горки, трение между телом и горкой отсутствует.

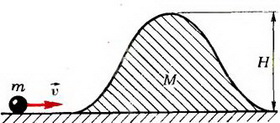
Рис. 6.

2. Под каким углом β разлетаются два одинаковых гладких шарика после абсолютно упругого удара? До удара один из шариков покоился, а другой двигался со скоростью , направленной под углом α к линии центров шариков.

3. По гладкой поверхности стола могут двигаться кольцо радиусом R и находящийся внутри кольца маленький шарик. В некоторый момент шарик упруго соударяется с кольцом. До удара кольцо покоится, а шарик движется со скоростью , которая составляет угол α с радиусом, проведенным в точку удара. Найдите время до следующего удара.

4. Два гладких одинаковых шара массой М каждый покоятся на гладкий горизонтальной поверхности, касаясь друг друга. Третий шар такого же радиуса, но массой m движется по поверхности со скоростью , проходящей через точку касания неподвижных шаров. Определите скорости шаров после абсолютно упругого удара.

Ответы

1. Возможны два случая: а) тело преодолеет горку; б) тело не преодолеет горку.  Из законов сохранения импульса и механической энергии следует, что тело сумеет переехать через горку, если модуль его начальной скорости 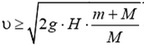. Тогда модули искомых скоростей тела и горки будут равны, соответственно.

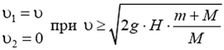
и

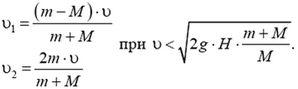
Заметим, что оба ответа являются решениями одной и той же системы уравнений, описывающей абсолютно упругое центральное соударение. В статье (см. задачу 1) мы ничего не говорили о первом решении, поскольку там оно описывало тривиальную ситуацию — отсутствие соударения.

2.

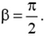
3.

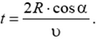
4. Первый шар будет двигаться в прежнем направлении, но модуль его скорости изменится и будет равен 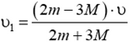. Второй и третий шары разлетятся под одинаковыми углами  к направлению движения первого шара с одинаковыми по модулю скоростями .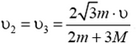

§5. Задачи на столкновения и законы сохранения импульса и энергии

В физике под столкновениями понимают процессы взаимодействия  между телами (частицами) в широком смысле слова, а не только в буквальном – как соприкосновение тел. Сталкивающиеся тела на большом расстоянии являются свободными. Проходя друг мимо друга, тела взаимодействуют между собой, в результате могут происходить различные процессы – тела могут соединиться в одно тело (абсолютно неупругий удар), могут возникать новые тела и, наконец, может иметь место упругое столкновение, при котором тела после некоторого сближения вновь расходятся без изменения своего внутреннего состояния. Столкновения, сопровождающиеся изменением внутреннего состояния тел, называются неупругими. Тела (частицы), участвующие в столкновении, характеризуются (до и после столкновения)  импульсами, энергиями. Процесс столкновения сводится к изменению этих величин в результате взаимодействия. Законы сохранения энергии и импульса позволяют достаточно просто устанавливать соотношения между различными физическими величинами при столкновении тел. Особенно ценным здесь является то обстоятельство, что зачастую законы сохранения могут быть использованы даже в тех случаях, когда действующие силы не известны. Так обстоит дело, например, в физике элементарных частиц.

Происходящие в обычных условиях столкновения макроскопи­ческих тел почти всегда бывают в той или иной степени неупругими – уже хотя бы потому, что они сопровождаются некоторым нагреванием тел, т. е. переходом части их кинетической энергии в тепло. Тем не ме­нее, в физике понятие об упругих столкновениях играет важную роль – с такими столкновениями часто приходится иметь дело в физическом эксперименте в области атомных явлений, да и обычные столкновения можно часто с достаточной степенью точности считать упругими.

Сохранение импульса тел (частиц) при столкновении обусловлено тем, что совокупность тел, участвующих в столкновении, составляет либо изолированную систему, т. е. на тела, входящие в систему, не действуют внешние силы, либо замкнутую: внешние силы отличны от нуля, а сумма внешних сил равна нулю. Несколько сложнее обстоит дело с применением закона сохранения энергии при столкновениях. Обращение к сохранению энергии  требует порой учёта различных форм внутренней энергии.

Можно сказать, что действие законов сохранения импульса и энергии в процессах столкновения подтверждено широким спектром опытных данных.

Переходя к характерным примерам, отметим, что исследование столкновений традиционно проводится как в лабораторной системе отсчёта (ЛСО), т. е. в инерциальной системе отсчёта, связанной с лабораторией, где проводится опыт, так и в системе центра масс, с которой Вы познакомитесь в следующих Заданиях. Напомним также, что центральным ударом шаров (шайб), называют удар, при котором скорости шаров (шайб) направлены вдоль прямой, проходящей через их центры.

Неупругие столкновения

Упругие столкновения

Построенное в общем виде решение задач упругого центрального и нецентрального соударений открывает дорогу к анализу целого ряда задач, для которых рассмотренная модель соответствует характеру взаимодействия тел (частиц). Приведём пример.

Заключение – дополнение к тексту

Мы применили закон сохранения импульса (одного из основных законов природы) к абсолютно неупругому и абсолютно упругому удару шаров.

При абсолютно неупругом ударе шары (тела) не сохраняют свою форму, то есть испытывают пластическую деформацию. К такому удару

можно отнести удар свинцовых шаров. При неупругом ударе не выполняется закон сохранения механической энергии, но выполняется закон сохранения полной энергии. При неупругом ударе механическая энергия полностью или частично переходит во внутреннюю энергию тел (тела нагреваются). В случае нецентрального (косого) удара тел их общий импульс и общая скорость после абсолютно неупругого удара находятся путём векторного сложения импульсов отдельных тел.

При абсолютно упругом ударе (сюда можно грубо приближённо отнести удар стальных шаров) выполняется и закон сохранения импульса, и закон сохранения механической энергии. При упругом ударе механическая энергия шаров частично или полностью переходит в потенциальную энергию упругой деформации. Затем тела принимают первоначальную форму, отталкивая друг друга. Потенциальная энергия упругой деформации снова переходит в кинетическую энергию шаров. Шары приобретают скорости

направления и модули которых определяются законами сохранения полного импульса и полной энергии системы. Последний 3) частный случай говорит о том, что если лёгкий шарик испытает абсолютно упругий удар о неподвижную стенку, то он отскочит от неё без потери скорости. Пусть теперь шарик падает на неподвижную стенку под углом.

Тогда нормальная составляющая скорости шарика изменит своё направление на обратное, а по модулю останется прежней. Тангенциальная же составляющая скорости не изменится, поэтому угол падения будет равен углу отражения.

На рисунке вектора скорости падения и скорости отражения шарика перенесены в точку падения. Вектор изменения скорости направлен вверх перпендикулярно поверхности стенки. Такие же направления имеют импульсы шарика до удара и после удара о стенку, а вектор приращения импульса шарика

направлен по нормали от стенки.

В молекулярной физике происходит то же самое, когда молекулы газа ударяются о стенку сосуда. Проявляется это давлением газа на стенку сосуда.

Подумаем, что можно найти, если в условии задачи сказано, что шарик летит под прямым углом к движущейся навстречу стенке и между ними происходит упругий удар:

Сразу можно сказать, что скорость шарика относительно движущейся стенки равна

(см. занятие 12 на относительность движения). От стенки шарик отскочит со скоростью

относительно стенки, а относительно земли его скорость после удара

Далее можно найти импульс шара относительно земли до и после удара. Сможем найти изменение его импульса, его кинетическую энергию до и после удара.

Изменение кинетической энергии даст работу, совершённую силой упругости за время удара. Работу же можно выразить через произведение силы удара на перемещение стенки за время удара и найти силу удара.

Таким образом, через данные в условии задачи сможем охарактеризовать упругий удар между шаром и движущейся стенкой.

Абсолютно неупругий удар и абсолютно упругий удар – это предельные случаи кратковременного взаимодействия шаров (тел). При взаимодействии реальных тел имеют место и упругие, и неупругие деформации. Формула, связывающая скорости шаров до удара и после удара имеет вид:

коэффициент восстановления относительной скорости при ударе. В случае абсолютно неупругого удара он равен нулю; в случае абсолютно упругого удара он равен единице.

При ударе реальных тел этот коэффициент принимает промежуточные значения между нулём и единицей. Для стали этот коэффициент равен 0,56.

К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.

Предыдущая запись: Занятие 23. Импульс системы тел. Центр масс системы

Следующая запись:Задачи 1 – 4 к занятиям 22 – 24

Первая запись на канале: Занятие 1. Физика. Механика. Кинематика