Как найти расстояние пройденное автомобилем

Время, скорость, расстояние

Расстояние

Мы постоянно ходим пешком и ездим на транспорте из одной точки в другую. Давайте узнаем, как можно посчитать это пройденное расстояние.

Расстояние — это длина от одного пункта до другого.

Расстояние обозначается латинской буквой s.

Единицы расстояния чаще всего выражаются в метрах (м), километрах (км).

Формула пути

Чтобы найти расстояние, нужно умножить скорость на время движения:

s = v × t

Скорость

Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.

Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.

Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.

Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.

Формула скорости

Чтобы найти скорость, нужно разделить путь на время:

v = s : t

Показатели скорости чаще всего выражаются в м/сек или км/час.

Скорость сближения — это расстояние, которое прошли два объекта навстречу друг другу за единицу времени. Чтобы найти скорость сближения, нужно сложить скорости объектов.

Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, которые движутся в противоположных направлениях.

Чтобы найти скорость удаления, нужно сложить скорости объектов.

Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.

Время

Время — самое дорогое, что у нас есть. Но кроме философии, у времени есть важная роль и в математике.

Время — это продолжительность каких-то действий, событий.

Время движения обозначается латинской буквой t.

Чаще всего вам будут встречаться такие единицы времени, как секунды, минуты и часы.

Формула времени

Чтобы найти время, нужно разделить расстояние на скорость:

t = s : v

Эта формула пригодится, если нужно узнать, за какое время тело преодолеет то или иное расстояние.

Взаимосвязь скорости, времени, расстояния

Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.

Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.

Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес-браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?

Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров на 15, мы определим расстояние от дома до магазина:

s = v × t = 50 × 15 = 750 м

Ответ: мы прошли 750 метров.

Если известно время и расстояние, то можно найти скорость: v = s : t.

Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние между двором и площадкой — 100 метров. Первый школьник добежал за 25 секунд, второй за 50 секунд. Кто добежал быстрее?

Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников — это расстояние, которое они пробегают за 1 секунду.

Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:

Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).

В нашей задаче расстояние дано в метрах, а время в секундах. Значит, будем измерять скорость в метрах в секунду (м/с).

Так мы узнали, что скорость движения первого школьника 4 метра в секунду.

Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:

Значит, скорость движения второго школьника составляет 2 метра в секунду.

Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.

Скорость первого школьника больше. Значит, он добежал до спортивной площадки быстрее.

Ответ: первый школьник добежал быстрее.

Если известны скорость и расстояние, то можно найти время: t = s : v.

Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?

Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?

Чтобы ответить на этот вопрос, нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое дойдем до стадиона:

t = s : v = 500 : 100 = 5 м

Ответ: от школы до стадиона мы дойдем за 5 минут.

Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Записаться на марафон

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Источник

Формула нахождения значений скорости, времени и расстояния

С древних времен людей беспокоит мысль о достижении сверх скоростей, так же как не дают покоя раздумья о высотах, летательных аппаратах. На самом деле это два очень сильно связанных между собой понятия. То, насколько быстро можно добраться из одного пункта в другой на летательном аппарате в наше время, зависит полностью от скорости. Рассмотрим же способы и формулы расчета этого показателя, а также времени и расстояния.

Как же рассчитать скорость?

На самом деле, рассчитать ее можно несколькими способами:

Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.

Теперь нужно подставить имеющиеся значения вместо буквенных символов:

v=100 км/1,5 ч=66,66 км/ч

Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.

Таким нехитрым способом можно найти скорость через время и расстояние.

А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:

Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:

Можно записать использовать и такой вид вычислений:

Но можно записать эту же формулу и в более точном варианте:

Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.

Другие способы вычисления

Существую и другие способы и методы, которые помогают вычислить значения рассматриваемого параметра. В пример можно привести формулу вычисления мощности:

Способы вычисления расстояния и времени

Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:

Таким образом вычисляется значение расстояния.

Или вычисляем значение времени, за которое пройдено расстояние:

Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.

Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.

И это еще не предел!

Видео

В нашем видео вы найдете интересные примеры решения задач на нахождение скорости, времени и расстояния.

Источник

Как правильно вычислить дистанцию, тормозной и остановочный путь автомобиля: формулы расчета

Формулы расчета остановочного и тормозного пути, а также безопасной дистанции.

В теоретическом экзамене есть вопрос о среднем времени реакции водителя, правильным ответом на который является 1 секунда. Также в билетах ГИБДД имеется вопрос, связанный с безопасной дистанцией. Есть вопросы, касаемые торможения. Но, как говорится, теория – это теория, которая, увы, с практикой, как правило, не имеет ничего общего.

Во-первых, то, что вы учили в билетах, является теорией, основанной на усредненных значениях и различных исследованиях. Фактически же время реакции водителя, остановочный и тормозной путь зависят от многих факторов и не могут быть точно рассчитаны для всех случаев. Тем не менее каждый водитель должен уметь рассчитывать эти параметры хотя бы приблизительно.

Тормозной путь автомобиля

Тормозной путь – это расстояние, которое будет пройдено автомобилем между контактом водителя с педалью тормоза и полной остановкой транспортного средства. Также стоит понимать различия между «нормальным торможением» и «экстренным торможением». В том числе не нужно забывать, что погодные условия влияют на тормозной путь. Если на дороге есть снег, тормозной путь, естественно, увеличивается.

Вот формула расчета тормозного пути:

Пример расчета: представим, что вы едете со скоростью 50 км/ч по городу и подъезжаете к пешеходному переходу, по которому идут дети. Расчет: (50 км/ч : 10) х (50 км/ч : 10) = 25 (метров). Таким образом, тормозной путь вашей машины составляет 25 метров. Поэтому вы должны учитывать длину тормозного пути, чтобы спокойно своевременно начать тормозить и остановиться перед пешеходным переходом.

Имейте в виду, что при экстренном торможении вы обычно нажимаете педаль тормоза полностью. В этом случае, как правило, тормозной путь сокращается вдвое. Вот формула тормозного пути при экстренном торможении:

Пример расчета: вы едете по городу со скоростью 50 км/ч, и вдруг на дорогу выкатывается мяч, за ним бежит ребенок. Вам нужна экстренная остановка автомобиля. Расчет: (50 км/ч : 10) х (50 км/ч : 10)/2 = 12,5 (метров). Тормозной путь вашей машины при экстренном торможении составит 12,5 метра.

Время и путь реакции водителя

Время реакции водителя – это время, которое пройдет с момента обнаружения водителем опасности на дороге до начала принятия мер по ее предотвращению.

Путь реакции водителя – это путь, который пройдет автомобиль с момента обнаружения водителем опасности на дороге до нажатия педали тормоза.

Вот формула расчета пути, который пройдет автомобиль в момент реакции водителя на опасность:

(Скорость в км / ч: 10) x 3 = путь реакции в метрах

Пример расчета: представим, что вы едете со скоростью 100 км/ч по проселочной дороге и внезапно на дорогу выбегает лось. Расчет: (100 км/ч : 10) х 3 = 30 (метров). То есть, после того как вы среагируете на опасность на дороге, ваша машина проедет примерно 30 метров. Добавьте к этому тормозной путь автомобиля.

Внимание: эти правила не являются научно правильными формулами и дают только приблизительное значение!

Остановочный путь автомобиля

Остановочный путь – это расстояние, пройденное транспортным средством с момента обнаружения водителем опасности на дороге до полной остановки машины.

Если вы хотите рассчитать остановочный путь автомобиля, вы должны добавить к тормозному пути автомобиля путь, пройденный за время реакции водителя. Вот как это можно сделать:

Первое значение в выражении – это путь реакции водителя, пройденный автомобилем, пока водитель реагирует на опасность на дороге. Второе выражение – это формула расчета тормозного пути. Для того чтобы вычислить остановочный путь транспортного средства, необходимо оба результата сложить вместе.

Пример расчета: вы едете на своей машине со скоростью 50 км/ч. Расчет: (50 км/ч : 10) х 3 = 15 метров пути проедет машина при реагировании на опасность на дороге (50 км/ч : 10) x (50 км/ч : 10) = 25 метров составит тормозной путь автомобиля. В итоге, сложив оба значения, получаем, что остановочный путь транспортного средства составит 40 метров.

Внимание: эти правила не являются научно правильными формулами и дают только приблизительное значение!

Дистанция

Источник

Вот как можно рассчитать тормозной путь: Формула

Как рассчитать расстояние тормозного пути автомобиля.

Как быстро автомобиль ускоряется, наверное, знает большинство автовладельцев. Даже если вы не замеряли динамику разгона своей машины, вы наверняка смотрели заводские технические характеристики вашего авто, где обычно автопроизводитель указывает минимально возможное время разгона с 0-100 км/час. Но теперь вопрос: сколько времени нужно, чтобы остановить вашу машину? Вы знаете это? Уверены, что нет. Но, оказывается, рассчитать расстояние тормозного пути можно достаточно легко с помощью простой формулы. Мы расскажем вам, как это делается.

Нет такой вещи во Вселенной или материи, которая может мгновенно остановиться. Также и любой автомобиль, когда вы нажимаете педаль тормоза, не сразу может остановиться. Дело в том, что для того чтобы автомобиль или любой объект в нашем мире остановился, необходимо, чтобы он потерял энергию, которая его движет. В результате у любого автомобиля есть тормозной путь, который он проезжает с момента нажатия педали тормоза до момента полной остановки. Это и есть тормозное расстояние машины.

Но на самом деле тормозной путь любого авто зависит не только от его характеристик и тормозной системы, но и от реакции водителя при нажатии педали тормоза. Ведь для того чтобы принять решение о необходимости торможения и нажать педаль тормоза, требуется время, которое хоть и минимально, но достаточно, чтобы машина успела проехать немаленький путь. Особенно это важно при большой скорости движения, где за какие-то доли секунды автомобиль проезжает приличное расстояние. Итак, в итоге, чтобы рассчитать реальную длину тормозного пути, нужно учитывать не только время и расстояние, пройденное автомобилем с момента нажатия водителем педали тормоза до момента остановки машины, но и время, необходимое для принятия решения о торможении. Дело в том, что при принятии решения о торможении мы тратим драгоценные секунды. Вот пример:

Кроме того, даже при нажатии педали тормоза есть еще небольшая потеря времени, связанная с тем, что при нажатии педали тормоза автомобиль, как правило, не начинает резко тормозить. А для того чтобы машина реально начала резко снижать скорость, надо усилить давление на педаль тормоза (пороговое время, необходимое для требуемого тормозного давления в тормозной системе). Также у всех автомобилей разное время отклика на нажатую педаль тормоза. Здесь все, конечно, зависит от конструкции тормозной системы и наличия различной электроники, контролирующей тормоза автомобиля.

Вы не поверите, но для того чтобы машина реально начала тормозить после нажатия педали тормоза, необходима еще почти 1 секунда времени. Вы представляете, как это много при движении на большой скорости? За эту лишнюю секунду вы можете проехать очень большой путь.

Что такое формула тормозного пути?

В общем, торможение автомобиля делится на два вида. Например, есть нормальное торможение, а есть экстренное, когда вам нужно резко остановить машину, чтобы избежать аварии.

При торможении в повседневной жизни, допустим, если вы хотите остановить автомобиль на светофоре, вы обычно нажимаете педаль тормоза намного плавнее и мягче, чем при необходимости полностью остановить автомобиль на парковке во дворе. В этом случае вы не применяете в машине максимальное тормозное усилие. При таком плавном и мягком торможении, как правило, тормозной путь (тормозное расстояние) увеличивается. Примерное расстояние тормозного пути при нормальном торможении можно рассчитать по следующей простой формуле:

(Скорость в км/ч : 10) x (скорость в км/ч : 10) = тормозной путь в метрах

При экстренном торможении педаль тормоза, как правило, нажата целиком и с полной силой. Из-за более высокой силы торможения обычно тормозной путь машины сокращается примерно в 2 раза. Поэтому длину тормозного пути можно также вычислить по следующей формуле:

(Скорость в км/ч : 10) x (скорость в км/ч : 10) / 2 = тормозной путь в метрах

Внимание: Вычисляемый по этим формулам тормозной путь является лишь приблизительным значением и подсказкой для водителей. На самом деле в реальности тормозной путь может быть как меньше, так и больше. Ведь расстояние тормозного пути зависит от навыков и опыта вождения водителя, от технической исправности автомобиля, его конструкции, марки, модели, состояния дорог, состояния протектора резины и многих других факторов, которые напрямую влияют на длину тормозного пути. Но благодаря этим формулам вы примерно сможете высчитать среднюю длину тормозного пути машины при определенной скорости движения. Это позволит вам скорректировать ваш стиль управления автомобилем, а также станет хорошим пособием для водителей-новичков.

Как рассчитать полное время остановки и итоговый тормозной путь?

Как мы уже сказали, чтобы рассчитать весь тормозной путь, нужно учитывать потерю времени при принятии водителем решения о торможении (то есть время реакции водителя). Для этого нужно использовать другую формулу, которая обеспечивает более точный приблизительный расчет тормозного расстояния, которое проедет автомобиль в момент принятия решения о необходимости остановки. Вот эта формула:

(Скорость в км/ч : 10) x 3 = путь реакции в метрах

В итоге, сделав вычисление по вышеуказанным формулам, вы можете вычислить приблизительный итоговый тормозной путь вашего автомобиля при любой скорости движения. Вот пример. Если вы управляете своим автомобилем со скоростью 50 км/ч, то с помощью приведенных формул вычислите следующие значения:

Примечание: Обратите внимание, что если скорость автомобиля будет выше всего в два раза, его итоговый тормозной путь увеличится в четыре раза.

То есть мнение о том, что при увеличении скорости автомобиля в два раза тормозной путь увеличивается только в два раза, – это чистый воды миф среди многих автолюбителей. Так что имейте это в виду, когда садитесь за руль. Самое удивительное, что об этом не знают даже многие опытные водители.

Пример расчета тормозных и остановочных расстояний

Источник

Расчет тормозного пути

Калькулятор тормозного пути позволит оценить тормозной путь автомобиля, движущегося с заданной скоростью. Для использования укажите тип дорожного покрытия, на котором тормозит автомобиль и скорость, при которой начинается торможение. Калькулятор рассчитает сколько метров пройдет автомобиль при торможении.

Калькулятор тормозного пути

Формула тормозного пути

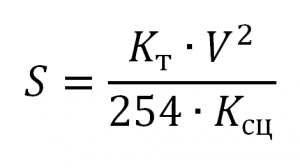
Формула для нахождения тормозного пути

Формула для нахождения тормозного пути применяется в подразделениях ГИБДД. Именно она используется в нашем калькуляторе. В этой формуле:

Кт — тормозной коэффициент (для легкового автомобиля равен 1),

V — скорость автомобиля,

Kсц — коэффициент сцепления.

Понятия и пояснения

Тормозной путь — это путь, который проходит автомобиль с момента, когда сработал тормозной механизм до полной остановки автомобиля. На него влияют:

Остановочный путь — путь с момента обнаружения опасности до полной остановки автомобиля. Понятно, что тормозной путь входит в остановочный. Кроме того в остановочный путь входят:

Первый параметр зависит от множества факторов, определяющим из которых является времени реакции водителя. По результатам многочисленных экспериментов, оно может меняться от 0,3 до 1,5 секунды. В среднем можно считать время реакции водителя равное 1 секунде. Кроме этого существует понятие «нормативное время восприятия сложной ситуации» равное 0,8 секунды. Также установлено, что время реакции у женщин, при возникновении сложной дорожной ситуации может достигать 2,5-3 секунд, тогда как у мужчин 1,5-2 секунды. Кроме этого на время реакции влияет:

Время срабатывания тормозной системы зависит от ее типа и технического состояния. Тормозная система с гидравлическим приводом срабатывает за 0,2 – 0,3 секунды, с пневматическим за 0,5 –0,6 секунд.

Источник

Задачи на движение (скорость, время и расстояние) являются одной из основных типов задач по математике, которые должен уметь решать каждый школьник. В данной статье рассмотрены все типы задач на движение:
— простые задачи на скорость, время и расстояние;
— задачи на встречное и противоположное движение;
— задачи на движение в одном направлении (на сближение и удаление);
— решение задач на движение по реке.

Скорость, время и расстояние: определения, обозначения, формулы

скорость = расстояние: время — формула нахождения скорости;

время = расстояние: скорость — формула нахождения времени;

расстояние = скорость · время — формула нахождения расстояния.

Скорость – это расстояние, пройденное за единицу времени: за 1 секунду, за 1 минуту, за 1 час и так далее.
Пример обозначения: 7 км/ч (читается: семь километров в час).
Если весь путь проходится с одинаковой скоростью, то такое движение называется равномерным.

На сайте представлены калькуляторы онлайн, с помощью которых можно перевести скорость, время и расстояние в другие единицы измерения:

1.Конвертер единиц измерения скорости
2.Конвертер единиц измерения времени
3.Конвертер единиц измерения расстояния (длины)

Примеры простых задач.

Задача 1. 

Автомобиль проехал 180 км за 2 часа. Чему равна скорость автомобиля?
Решение: 180:2=90 (км/ч.)
Ответ: Скорость автомобиля равна 90 км/ч.

Задача 2. 

Автобус проехал путь в 240 км со скоростью 80 км/ч. Сколько времени ехал автобус?
Решение: 240:80=3 (ч.)
Ответ: Автобус проехал 3 часа.

Задача 3. 

Грузовик ехал 5 часов со скоростью 70 км/ч. Какое расстояние проехал грузовик за это время?
Решение: 70 · 3 = 350 (км)
Ответ: Грузовик за 5 часов проехал 350 км.

Задачи на встречное движение

В таких задачах два объекта движутся навстречу друг другу.
Задачи на встречное движение можно решать двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость сближения объектов (как сумму их скоростей), общие время и расстояние. Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.

Задача 4. 

Из двух пунктов навстречу друг другу одновременно выехали два поезда и встретились через 3 часа. Первый поезд ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. На каком расстоянии друг от друга находятся пункты?
Решение: 
Первый способ. Найти расстояние, которое проехал каждый автобус, и сложить полученные данные:
80*3=240 (км) – проехал 1й автобус, 70*3=210 (км) – проехал 2й поезд,
240+210=450 (км) – проехали два поезда.
Второй способ. Найти скорость сближения поездов, то есть на сколько сокращалось расстояние между ними каждый час; а затем найти расстояние:
80+70=150 (км/ч), 150*3=450 (км).
Ответ: города находятся на расстоянии 450 км.

Задача 5. 

Из двух городов навстречу друг другу одновременно выехали два автобуса. Первый автобус ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. Какое расстояние будет между ними через 2 часа, если расстояние между городами 450 км?
Решение: 
Первый способ. Определить, сколько километров проехал каждый автобус и найти расстояние, которое осталось проехать:
80*2=160 (км)-проехал 1й автобус, 70*2=140 (км)-проехал 2й автобус,
160+140=300 (км)-проехали два автобуса, 450-300=150 (км)-осталось проехать.
Второй способ. Найти скорость сближения автобусов и умножить ее на время в пути.
80*70=150 (км/ч) – скорость сближения; 150*2=300 (км) – проехали два автобуса; 450-300=150 (км) – осталось проехать.
Ответ: Через 2часа расстояние между автобусами будет 150 км.

Задачи на движение в противоположных направлениях

В таких задачах два объекта движутся в противоположных направлениях, отдаляясь друг от друга. В таком типе задачи используется скорость удаления. Задачи на движение в противоположных направлениях также можно решить двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость удаления объектов (как сумму их скоростей), общие время и расстояние. Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.

Задача 6. 

Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля 100 км/ч, скорость второго – 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
Решение: 
Первый способ. Определить расстояние, которое проехал каждый автомобиль и найти сумму полученных результатов:
1) 100 · 4 = 400 (км) – проехал первый автомобиль
2) 70 · 4 = 280 (км) – проехал второй автомобиль
400 + 280 = 680 (км)
Второй способ. Найти скорость удаления, то есть значение увеличения расстояния между автомобилями за каждый час, а затем скорость удаления умножить на время в пути.
100 + 70= 170 км/ч – это скорость удаления автомобилей.
170 · 4 = 680 (км)
Ответ: Через 4 часа между автомобилями будет 680 км.

Задача 7. 

Из двух населённых пунктов, расстояние между которыми 40 км, вышли в противоположных направлениях два туриста. Первый турист шёл со скоростью 4 км/ч, а второй — 5 км/ч. Какое расстояние между туристами будет через 5 часов?
Решение: 
Первый способ. Определить сколько километров прошёл каждый из туристов за 5 часов, сложить полученные результаты, а затем к полученному расстоянию прибавить расстояние между населенными пунктами.
1) 4 · 5 = 20 (км) – прошёл первый турист;
2) 5 · 5 = 25 (км) – прошёл второй турист;
3) 20 + 25 = 45 (км);
4) 45 + 40 = 85 (км).
Второй способ. Найти скорость удаления пешеходов, затем найти пройденное расстояние, к полученному результату прибавить расстоянием между населёнными пунктами.
4 + 5 = 9 (км/ч);
9 · 5 = 45 (км);
45 + 40 = 85 (км);
Ответ: Через 5 часов расстояние между пешеходами будет 85 км.

Задачи на движение в одном направлении

В таких задачах два объекта движутся в одном направлении с разной скоростью, при этом они сближаются друг с другом или отдаляются друг от друга. Соответственно находится скорость сближения или скорость удаления объектов.

Формула нахождения скорости сближения или удаления двух объектов, которые движутся в одном направлении: из большей скорости вычесть меньшую.

Задача 8. 

Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?,
Решение: 
Задачу можно решить с помощью уравнения.
В этом случае скорость первого автомобиля 40 км/час, время в пути на 4 часа больше, чем время второго автомобиля (или t+4). Скорость второго автомобиля 60 км/час, время в пути – t. Расстояние оба автомобиля проехали одинаковое. Поэтому можно составить уравнение: 40*(t+4)=60*t. Отсюда получаем t=8 (часов) – время в пути второго автомобиля, за которое он догонит первый.
Решение задачи без использования уравнения.
Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на: 40 · 4 = 160 (км).
Второй автомобиль движется быстрее первого, значит, каждый час расстояние между автомобилями будет сокращаться на разность их скоростей: 60 — 40 = 20 (км/ч) – это скорость сближения.
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся: 160 : 20 = 8 (ч)
Ответ: Второй автомобиль догонит первый через 8 часов.

Задача 9. 

Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов: 5 — 4 = 1 (км/ч).
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого: 5 : 1 = 5 (ч)
Ответ: Через 5 часов второй пешеход догонит первого.

Задача 10. 

Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго – 40 км/ч.
1) Чему равна скорость удаления между автомобилями?
2) Какое расстояние будет между автомобилями через 3 часа?
3) Через сколько часов расстояние между ними будет 200 км?
Решение: 
1) 80 — 40 = 40 (км/ч) — скорость удаления автомобилей друг от друга.
2) 40 · 3 = 120 (км) – расстояние между ними через 3 часа./
3) 200 : 40 = 5 (ч) – время, через которое расстояние между автомобилями станет 200 км.
Ответ:
1) Скорость удаления между автомобилями равна 40 км/ч.
2) Через 3 часа между автомобилями будет 120 км.
3) Через 5 часов между автомобилями будет расстояние в 200 км.

Задачи на движение по реке

Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.

Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки. Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.

Задача 11. 

Лодка движется по реке. За сколько часов она преодолеет расстояние 120 км, если ее собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?
Решение: 
1) лодка движется по течению реки.
27 + 3 = 30 (км/ч) – скорость лодки по течению реки.
120 : 30 = 4 (ч) – проплывет путь.
2) лодка движется против течения реки.
27 — 3 = 24 (км/ч) — скорость лодки против течения реки
120 : 24 = 5 (ч) – проплывет путь.
Ответ:
1) При движении по течению реки лодка потратит 4 часа на путь.
2) При движении против течения реки лодка потратит 5 часов на путь.

Итак, для решения задач на движение:

1. Основная формула:S=ν*t;
2. Нужно сделать чертеж, который поможет определить тип задачи.
3. Все цифры нужно привести в единые единицы измерения: длина и время

Заключение.

Решая много задач по данной теме, ученик обязательно научится быстро ориентироваться в понятиях «скорость», «время» и «расстояние» и быстро решать задачи всех типов.

Весь курс начальной школы (за 1-4 классы) в краткой форме на сайте edu.intmag24.ru. С помощью курса можно быстро повторить основные моменты и правила по предметам: русский язык, математика, окружающий мир.

Для решения более сложных задач на движение посмотрите, как составлять схемы и таблицы данных для наглядного представления и структурирования данных.

А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:

vср=(v1+v2+v3+…+vn)/n

где v1, v2, v3, vn – значения скоростей объекта на отдельных участках пути S,

n – количество этих участков,

vср – средняя скорость объекта на всем протяжении всего пути.

Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:

vср=(S1+S2+…+Sn)/t,

где vср – средняя скорость объекта на всем протяжении пути,

S1, S2, Sn – отдельные неравномерные участки всего пути,

t – общее время, за которое объект прошел все участки.

Можно записать использовать и такой вид вычислений:

vср=S/(t1+t2+…+tn),

где S – общее пройденное расстояние,

t1, t2, tn – время прохождения отдельных участков расстояния S.

Но можно записать эту же формулу и в более точном варианте:

vср=S1/t1+S2/t2+…+Sn/tn,

где S1/t1, S2/t2, Sn/tn – формулы вычисления скорости на каждом отдельном участке всего пути S.

Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.