$begingroup$
Suppose, we know that $tau$ is the average time between succesive collisions, for finding the displacement, we can multiply $tau$ with drift velocity, however, is it actually possible to find out the distance covered within succesive collisions?
Thanks.
asked May 19, 2021 at 16:52
$endgroup$
5
$begingroup$
In the classical model, the free electrons are bouncing around in thermal equilibrium with the atoms of the conductor. Their average speed would be:
V = $(3kT/m)^.5$ = d/ τ.
Where d is the average distance traveled between atoms on each bounce, and τ is the mean free time. In each bounce, they are accelerated in the direction of electron flow by the electric field giving an average drift velocity:
v = [(eE/2m)$τ^2$]/ τ = eEτ/2m.
A previous question gives methods for finding v. Use that in my second equation to get τ, and τ in the first equation to get d.
answered May 19, 2021 at 19:12
$endgroup$
Закон движения электрона в магнитном поле
Содержание:
- Каково движение электрона в магнитном поле
-
Как найти скорость
- Траектория движения
- Период обращения электрона в магнитном поле
- Отклонение электронов в магнитном поле
- Примеры решения задач
Каково движение электрона в магнитном поле
Известно, что магниты представляют собой металлы, обладающие свойством к притяжению прочих магнитов и металлических предметов определенного состава. Во внутренней области таких объектов сгенерировано магнитное поле, действие которого можно наблюдать в реальных условиях. Эффект проявляется по-разному, то есть магнит отталкивает или притягивает предметы.
Роль источника, формирующего магнитное поле, играют заряженные частицы, которые пребывают в движении. Если перемещение зарядов обладает определенным направлением, то такой процесс называют электрическим током. Таким образом, легко сделать вывод об образовании магнитного поля, благодаря наличию электричества.
Электрический ток ориентирован по перемещению зарядов со знаком плюс и направлен противоположно относительно передвижения частиц, которые заряжены отрицательно. Если предположить, что имеется некая трубка в форме кольца с потоком воды, то какой-то ток примет противоположное ему направление. Электрический ток записывают с помощью буквы I.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Если рассматривать металлические предметы, то в них образование тока связано с перемещением отрицательных зарядов. На наглядном изображении продемонстрировано передвижение частиц, заряженных отрицательно, то есть электронов, в левую сторону. В то время как электричество ориентировано в правую сторону.
Источник: habr.com
В начале исследований электричества ученые не обладали информацией о природе и свойствах носителей электрического тока. При рассмотрении аналогичного проводника слева, как на рисунке выше, можно заметить, что ток перемещается от наблюдателя, а магнитное поле окружает его по часовой стрелке.
Источник: habr.com
Эксперимент можно продолжить, используя компас. При размещении прибора около проводника, изображенного на схеме, произойдет разворот стрелки перпендикулярно относительно рассматриваемого проводника, параллельно по отношению к силовым линиям магнитного поля, то есть параллельно кольцевой стрелке, обозначенной черным цветом на изображении.
Представим, что имеется некий шарообразный предмет, заряженный положительно. Заряд со знаком плюс обусловлен недостаточным количеством электронов. Данному шарику можно задать направление путем подбрасывания вперед. В таком случае вокруг объекта сформируется аналогичное предыдущему примеру магнитное поле кольцевого типа, которое закручивается вокруг шарика по направлению часовой стрелки.
Источник: habr.com
В данном случае заряженные частицы перемещаются в определенном направлении. Таким образом, целесообразно сделать вывод о наличии электрического тока. В результате при возникновении электричества вокруг него формируется магнитное поле. Передвигающийся заряд, либо какое-то количество таких частиц, формирует около себя «тоннель» в виде магнитного поля. При этом стенки «тоннеля» более плотные около перемещающейся заряженной частицы.
Удаляясь от перемещающегося заряда, напряженность, то есть сила генерируемого магнитного поля, слабеет. В результате компасная стрелка меньше реагирует на него. Закон, согласно которому напряженность рассматриваемого поля распределяется около источника, аналогичен закономерности формирования электрического поля вокруг заряда. Таким образом, величина напряженности и квадрат расстояния до источника находятся в обратной пропорциональной зависимости.
Рассмотрим следующую ситуацию, когда шарик с положительным зарядом движется по траектории в форме круга. В таком случае кольцевые линии магнитных полей, сформированных вокруг предмета, складываются. В итоге получается магнитное поле, обладающее перпендикулярным направлением относительно плоскости, в рамках которой происходит движение заряженного шарика.
Источник: habr.com
Заметим, что «тоннель» магнитного поля, образованный около заряженного объекта, сворачивается, и получается кольцо, которое схоже по форме с бубликом. Аналогичную ситуацию можно наблюдать в процессе сворачивания в кольцо проводника с электричеством. Тогда проводник, деформированный так, что получается катушка с множеством витков, называют электромагнитом. Около подобного предмета формируются магнитные поля за счет перемещающихся в нем зарядов, то есть электронов.
При условии вращения шарика с зарядом вокруг собственной оси возникает магнитное поле по аналогии с тем, что образовано у нашей планеты, которое ориентировано вдоль оси вращательного движения. Тогда имеет место возникновение кругового электрического тока, который определяют как ток, провоцирующий образование магнитного поля во время перемещения по круговой траектории заряженной частицы относительно оси шарика.
Источник: habr.com
В этом случае процесс аналогичен перемещению шарика по кругу. Отличие состоит в том, что радиус орбиты движения уменьшен до величины радиуса шарообразного объекта. Вышеизложенные выводы имеют смысл и тогда, когда заряд шарика имеет знак минуса, а магнитное поле ориентировано противоположно.
Описанный выше эффект удалось выявить экспериментальным путем Роуланду и Эйхенвальду. Исследователи фиксировали магнитные поля около дисков, обладающих зарядом и совершающих вращательные движения. Вблизи этих объектов замечали отклонения компасной стрелки. Ознакомиться с наглядным представлением опыта можно на рисунке ниже:
Источник: habr.com
На изображении отмечены направления магнитных полей, которые зависят от положительного или отрицательного заряда дисков, расположенных в системе. По рисунку заметно, как эти направления меняются при смене знака заряда. Если диск, не обладающий зарядом, привести во вращательное движение, то магнитное поле отсутствует. Стационарные заряды также не образуют вокруг себя поля.
Как найти скорость
В плане изучения интересен процесс перемещения зарядов в пространственной области при наличии магнитного и электрического поля. Применительно к такой ситуации целесообразно воспользоваться соотношением для силы Лоренца, которая представляет собой суммарную величину сил, оказывающих воздействие на заряд, перемещающийся в электрическом и магнитном полях.
Представим, что заряд равен q и перемещается со скоростью (overrightarrow{v}) в условиях однородного магнитного поля, индукция которого составляет (overrightarrow{В}), а также в присутствии электрического поля с определенной напряженностью (overrightarrow{N}). Запишем силу воздействия электрического поля на заряд по модулю:
(Fэ = qE)
Этот компонент силы Лоренца принято называть электрической составляющей. Применительно к магнитному полю, на перемещающийся заряд воздействует магнитная составляющая силы Лоренца. Модуль определяют по закономерности Ампера. Представим, что проводник, по которому течет электричество, расположен в однородном магнитном поле. Вдоль этого объекта перемещаются заряды. Проанализирует ситуацию на отрезке данного проводника, который в длину составляет (triangle l), а площадь его поперечного сечения равна S.
Источник: иванов-ам.рф
Формула для вычисления силы тока, протекающего по проводнику:
(I = qnυS)
Зная, что:
(F_{А} = BItriangle l sin alpha)
Получим следующее выражение:
(FA = BqnvSΔtriangle l sin alpha)
Здесь (N = nStriangle l) обозначает количество зарядов, входящих в объем (Striangle l).
Исходя из записанной формулы, несложно выразить скорость движения заряда с учетом второго закона Ньютона:
(v = frac{qBR}{m})
Траектория движения
Изучить направление, в котором перемещаются заряженные частицы в магнитном поле, целесообразно на примере простейшего случая. При этом происходит движение заряда в однородном магнитном поле с индукцией, которая является перпендикуляром исходной скорости заряженной частицы. Схематично передвижение заряда изображено на рисунке:
Источник: иванов-ам.рф
В связи со стабильным значением модуля скорости заряда, не меняется модуль магнитной составляющей силы Лоренца по аналогии. Исходя из того, что рассматриваемая сила является перпендикуляром к скорости, можно заключить наличие центростремительного ускорения у перемещающейся частицы. Данная величина также не меняется по модулю, что позволяет сделать вывод о постоянстве радиуса кривизны R рассматриваемой траектории. Таким образом, подтверждается ранее выведенная формула скорости:
(v = frac{qBR}{m})
Период обращения электрона в магнитном поле
Запишем математическое соотношение, позволяющее выразить период обращения заряженной частицы в магнитном поле:
(T=frac{2 cdot{pi}cdot r}{upsilon};)
(r=frac{m cdot upsilon}{|q| cdot B} Rightarrow T=frac{2 cdot pi cdot m}{|q| cdot B}.)
Отклонение электронов в магнитном поле
Из предыдущего анализа движения заряда известно, что процесс сопровождается воздействием на частицу, перемещающуюся в магнитном поле, силы Лоренца. Данная сила определяется величиной и знаком рассматриваемой частицы, а также зависит от быстроты ее перемещения и индукции магнитного поля. В итоге траектория, по которой движется заряд, изменяется. Опытным путем явление можно наблюдать с помощью системы магнитного поля и электронного луча осциллографа.
В ходе эксперимента необходимо выключить горизонтальную развертку луча и с помощью рукояток отрегулировать положение луча по вертикали и горизонтали. В результате последовательных манипуляций луч окажется направленным непосредственно в центральную область экрана. Следует расфокусировать образованное световое пятно, увеличивая яркость до максимально возможного значения. Если поместить рядом с прибором постоянный магнит, то можно наблюдать смещение пятна вбок, как изображено на рисунке:
Источник: duckproxy.com
Изменение положение пятна наблюдается в процессе приближения или удаления магнита от осциллографа. Таким образом, справедливо сделать вывод о том, что смещение пятна зависит от величины индукции магнитного поля. Если перевернуть магнит, то направление индукции изменится, а пятно на экране переместится в противоположную сторону.
Примеры решения задач
Задача 1
Созданы условия для движения электрона в однородном магнитном поле. Индукция данного поля составляет (B=4cdot {10}^{-3} {Тл}). Требуется вычислить, чему равен период обращения рассматриваемой отрицательно заряженной частицы.
Решение
В первую очередь следует записать данные из условия задачи. Так как речь в задании идет об электроне, то следует выписать справочные величины заряда и массы:
({q}_{e}=-1.6cdot {10}^{-19} {Кл})
({m}_{e}=9.1cdot {10}^{-31} {кг})
Вспомним формулу для расчета период обращения заряженной частицы в магнитном поле из ранее пройденного теоретического материала:
(T=frac{2 cdot{pi}cdot r}{upsilon}; r=frac{m cdot upsilon}{|q| cdot B} Rightarrow T=frac{2 cdot pi cdot m}{|q| cdot B})
Подставим численные значения и получим:
(T=frac{2 cdot 3.14 cdot 9.1cdot {10}^{-31},text{кг}}{|-1.6cdot {10}^{-19},text{Кл}| cdot 4cdot {10}^{-3},text{Тл}}=8.9cdot {10}^{-9},с)
Ответ: период обращения электрона в магнитном поле равен (8.9cdot {10}^{-9} с).
Задача 2
Имеется однородное магнитное поле, величина индукции которого составляет (10^{-3} Тл) . В это поле попадает отрицательно заряженная частица по направлению перпендикулярно относительно линий магнитной индукции и под углом (alpha=frac{pi}{4}) к границе рассматриваемого поля. Скорость электрона по модулю соответствует (10^{6} м/с). В направлении оси абсциссы и ординаты поле не имеет границ. Известно, что заряд частицы к ее массе относится как (frac{е}{m}=1,76cdot 10^{11} Кл/кг). Необходимо вычислить расстояние, на котором от точки взлета электрон покинет поле.
Решение
Изобразим схематично условие задания:
Источник: иванов-ам.рф
В данном случае целесообразно применить правило левой руки, чтобы определить направление силы Лоренца с учетом отрицательного заряда наблюдаемой частицы. Схематично это представлено на рисунке выше. В условиях воздействия магнитного поля электрон подвержен действию магнитной составляющей силы Лоренца. В результате отрицательно заряженная частица будет перемещаться по дуге окружности. Следует вычислить радиус этой окружности. Воспользуемся вторым законом Ньютона:
(moverrightarrow{a}=overrightarrow{F_{л}})
Поскольку центростремительное ускорение:
(а = frac{v^{2}}{R})
В результате получим, что:
(frac{mv^{2}}{R}=evB Rightarrow R=frac{mv}{eB})
При рассмотрении (triangle O^{,}OC) можно сделать вывод:
(OC = frac{l}{2} = R sin alpha)
Тогда:
(l = 2R sin alpha = 2frac{mv sin alpha}{eB})
При подстановке численных значений получим:
(l = frac{2cdot 10^{6} cdot sin frac{pi}{4}}{1,76 cdot 10^{11}cdot 10^{-3} } = 0,008м = 8 мм)
Ответ: 8 мм.
1. Движение вдоль линий напряженности
Рассмотрим сначала случай, когда действующей на тело силой тяжести можно пренебречь по сравнению с силой, которая действует на тело со стороны электрического поля. Это всегда имеет место, когда речь идет о движении заряженных микрочастиц, например электронов. Напомним, кстати, что электрон имеет отрицательный заряд, а протон – положительный.
? 1. Объясните, почему при рассмотрении движения частицы в электрическом поле нельзя пренебрегать массой частицы даже в том случае, когда сила тяжести пренебрежимо мала по сравнению с силой, действующей на частицу со стороны электрического поля.
? 2. Заряженная частица движется в однородном электрическом поле. Что можно сказать о начальной скорости этой частицы, если траектория ее движения – прямолинейная?
Рассмотрим, как при таком движении изменяется кинетическая и потенциальная энергия частицы.
? 3. Электрон движется прямолинейно в однородном электрическом поле из точки с потенциалом 700 В в точку с потенциалом 200 В.
а) Совпадает ли направление начальной скорости электрона с направлением линий напряженности поля или эти направления противоположны?
б) Как изменилась полная энергия электрона?
в) Чему равно изменение потенциальной энергии электрона?
г) Чему равно изменение кинетической энергии электрона?
д) Какова минимальная начальная скорость электрона?
При движении в электрическом поле заряженная частица может изменить направление движения на противоположное.
? 4. Электрон влетает в однородное электрическое поле с начальной скоростью 8 * 106 м/с. Потенциал поля в точке, в которую влетает электрон, равен 500 В. Направление начальной скорости электрона совпадает с направлением линий напряженности поля.
а) До точки с каким минимальным значением потенциала поля долетит электрон?
б) С какой по модулю скоростью электрон вернется в начальную точку?
в) Чему равна напряженность поля, если электрон вернулся в начальную точку через 9,1 * 10-9 с?
г) Чему равен путь, пройденный электроном до его возвращения в начальную точку?
Сравним движение в одном и том же поле двух частиц с одинаковыми по модулю зарядами, но с различными массами.
? 5. Электрон и протон находятся на одной линии напряженности однородного электрического поля на расстоянии 1 см друг от друга. Они начинают двигаться из состояния покоя в противоположные стороны.
а) Чему равна напряженность поля, если через 10-8 с расстояние между частицами стало равным 9,8 см?
б) На какое расстояние от своей начальной точки удалился к этому моменту протон?
в) Чему равны в этот момент скорости электрона и протона?
2. Движение заряженной частицы в конденсаторе
Если силой тяжести можно пренебречь по сравнению с силой, действующей на заряженную частицу со стороны электрического поля, то ее движение в поле конденсатора будет аналогично движению тела, брошенного горизонтально или под углом к горизонту, только роль силы тяжести будет играть сила, действующая на заряженную частицу со стороны электрического поля.
? 6. По какой траектории будет двигаться заряженная частица в однородном электрическом поле, если ее начальная скорость направлена под углом к линиям напряженности поля?
При рассмотрении тела, брошенного горизонтально или под углом к горизонту, мы использовали горизонтально направленную ось координат x и вертикально направленную ось y. В данном случае также удобно ввести оси координат x и y, как показано на рисунке 56.1.
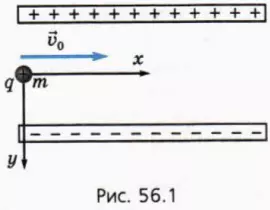
Если начальная скорость частицы направлена горизонтально, направление оси y удобно выбрать так, чтобы проекция силы, действующей на эту частицу со стороны электрического поля конденсатора, была положительной. Начало координат совместим с начальным положением частицы.
? 7. Частица с зарядом q и массой m влетает в электрическое поле плоского конденсатора в точке, находящейся посередине между пластинами (рис. 56.1). Пластины конденсатора расположены горизонтально. Расстояние между пластинами равно d, длина пластин l, напряжение между пластинами U. Начальная скорость частицы равна по модулю v0 и направлена горизонтально.
а) Чему равны проекции ускорения частицы на оси координат при ее движении внутри конденсатора?
б) Как зависят от времени проекции скорости частицы?
в) Как зависят от времени координаты частицы?
г) Сколько времени частица будет лететь сквозь весь конденсатор, если не столкнется с его пластиной?
д) При каком соотношении между указанными выше параметрами частица пролетит сквозь весь конденсатор и вылетит из него?
е) Чему равен тангенс угла между скоростью частицы и горизонталью в тот момент, когда частица вылетает из конденсатора?
ж) Чему равен модуль скорости частицы, когда она вылетает из конденсатора?
? 8. Электрон влетает в конденсатор посередине между его пластинами со скоростью, направленной параллельно пластинам. Расстояние между пластинами равно 1 см, длина пластин 10 см. Начальная скорость электрона 5 * 107 м/с.
а) Какова должна быть разность потенциалов между пластинами конденсатора, чтобы электрон не пролетел сквозь весь конденсатор?
б) На какую пластину в таком случае попадет электрон?
в) На каком расстоянии от положительной пластины будет находиться электрон в момент вылета из конденсатора, если напряжение между его пластинами равно 100 В?
г) Чему в этом случае будет равен тангенс угла между скоростью электрона и горизонталью в момент его вылета из конденсатора?
д) Как в этом случае изменится потенциальная энергия электрона за время его движения в конденсаторе?
е) На сколько процентов увеличится кинетическая энергия электрона за время движения в конденсаторе?
Рассмотрим случай, когда начальная скорость частицы направлена под углом к пластинам конденсатора.
Возможные типы траектории движения частицы схематически изображены на рисунке 56.2. Для определенности мы выбрали положительно заряженную частицу.
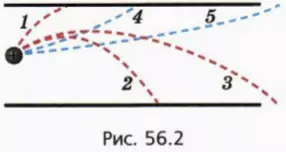
? 9. Каков знак заряда верхней пластины конденсатора, если положительно заряженная частица движется по одной из траекторий, изображенных красным пунктиром? синим пунктиром?
3. Движение заряженного тела в электрическом поле с учетом силы тяжести
Рассмотрим теперь случай, когда надо учитывать не только силу, действующую на тело со стороны электрического поля, но и силу тяжести.
? 10. Две большие пластины заряженного плоского конденсатора расположены вертикально (рис. 56.3). Разность потенциалов между пластинами равна U, а расстояние между ними равно d. Посередине между пластинами находится шарик с зарядом q и массой m. В начальный момент шарик покоится. Через некоторое время после того, как шарик отпустили, он столкнулся с одной из пластин конденсатора. Направим оси координат, как показано на рисунке.
56.3
а) Чему равна по модулю сила, действующая на шарик со стороны электрического поля?
б) Чему равна проекция ускорения шарика на ось х?
в) Через какой промежуток времени шарик столкнется с пластиной? Каков знак заряда этой пластины?
г) Насколько уменьшится высота шарика над землей к моменту столкновения по сравнению с его начальной высотой?
д) Какова форма траектории шарика?
е) Чему равно ускорение шарика во время движения?
ж) Чему равна скорость шарика в момент столкновения с пластиной?
Дополнительно вопросы и задания
11. Крупинка массой 10-5 г влетает в электрическое поле горизонтально расположенного плоского конденсатора в точке, находящейся посередине между пластинами. Верхняя пластина конденсатора заряжена положительно. Начальная скорость крупинки направлена горизонтально. Длина пластин конденсатора 10 см, расстояние между пластинами 1 см, напряжение между пластинами 1 кВ. Начальная скорость пылинки 6 м/с. Заряд крупинки равен по модулю 3 * 10-12 Кл.
а) Чему равно отношение модулей силы тяжести и силы, действующей на крупинку со стороны электрического поля? При каком знаке заряда крупинки эти силы направлены одинаково?
б) Чему равно и как направлено ускорение крупинки, если у нее избыток электронов? недостаток электронов?
в) При каком знаке заряда крупинки она пролетит конденсатор насквозь?
12. Заряженная частица влетает в однородное электрическое поле с начальной скоростью, перпендикулярной линиям напряженности поля. В момент вылета из поля направление ее скорости составляет угол 60º с направлением начальной скорости. Во сколько раз увеличилась кинетическая энергия частицы при движении в электрическом поле? Считайте, что силой тяжести можно пренебречь.
Взаимодействие
легких заряженных частиц со средой
Специфика:
-
В
силу малости массы, e±
движутся в веществе не по прямой и для
них существенны радиационные потери
энергии (на тормозное излучение). -
При
столкновениях e–
с электронами вещества надо учитывать
обменные эффекты. -
В
случае e+
возможен процесс его аннигиляции на
электроне вещества (σ(e++e–→2γ)
~ 1/u).
Ионизационные
потери легких заряженных частиц –
электронов.
Прохождение электронов через вещество
отличается от прохождения тяжёлых
заряженных частиц. Главная причина –
малая масса электрона. Это приводит к
относительно большому изменению импульса
электрона при каждом его столкновении
с частицами среды, что вызывает
заметное изменение направления движения
электрона и как результат – электромагнитное
радиационное излучение.
Удельные потери энергии электронов с
кинетической энергией

являются суммой ионизационных и
радиационных потерь.

Ионизационные потери энергии
электронами. В области низких энергий
электронов (E < 1 МэВ) определяющий
вклад в потери энергии дают неупругие
ионизационные процессы взаимодействия
с атомными электронами, включающие
ионизацию атомов. Передаваемая в одном
столкновении энергия в среднем очень
мала и при движении в веществе потери
складываются из очень большого числа
таких малых потерь. Статистические
флуктуации в ионизационных процессах
ведут к разбросу потерь и величин
пробегов.
В нерелятивистской области ионизационные
потери быстро уменьшаются при увеличении
энергии и достигают минимума при энергии
E ![]()
1.5
МэВ, Рис. .

Рис. Удельные ионизационные (1) и
радиационные (2) потери энергии электроном
в кремнии
Далее потери очень медленно (логарифмически)
растут с энергией, выходя на плато.
Причиной такой зависимости является
поляризация среды пролетающим электроном
(эффект плотности). В результате
ослабляется кулоновское поле
релятивистского электрона, и в плотных
средах (твёрдые тела, жидкости) потери
не растут. В газах рост потерь может
достигать нескольких десятков
процентов.
При расчётах
зависимости потерь учитывается движение
обоих электронов после взаимодействия
и то, что приведённая масса взаимодействующих
электронов равна me/2. Принимаются в
расчёт также квантовомеханические
эффекты тождественности электронов.
Относительная величина этих поправок
составляет несколько процентов.
Радиационные потери электронов (тормозное
излучение подробно будет рассмотрено
позднее).
Вывод формулы для потерь энергии на
ионизацию электронами в принципе такой
же, как и для других заряженных частиц.
Также для электронов (z=1) получается
соотношение:
![]()
Но величины bmin и bmax приходится выбирать
по-другому.
Необходимо при этом учитывать, что
1) падающие электроны в процессе
взаимодействия из-за малости
своей массы будут отклоняться от
первоначального направления;
2) из-за тождественности взаимодействующих
частиц будут возникать
обменные эффекты, имеющие квантовую
природу.
При учете этих замечаний формула для
удельных ионизационных
потерь электронов принимает вид:

.
В этой формуле
![]()
– релятивистская кинетическая энергия
электрона.
В нерелятивистском случае формула
сводится к более простому выражению:

В ультрарелятивистском случае при E
» mec2 формула для
потерь энергии также имеет простой вид:
![]()
В отличие от тяжелых частиц для электронов
важны оба эти предельных случая, так
как mec2=0,511 МэВ и электрон становится
ультрарелятивистским уже при энергии
в несколько МэВ.
Сравнение
ионизационных потерь для электронов и
тяжелых заряженных частиц приводит к
следующим выводам.
-
Множители перед квадратными скобками
в выражениях для ионизационных потерь
электронов и тяжелых заряженных частиц
одинаковы ( с точностью до множителя
2) , т.е. при одинаковых скоростях удельные
потери их одинаковы ( с точностью до
множителя 2).
Формула Бора

Формула Бете-Блоха
для тяжелых заряженных частиц

Для электронов

-
При одной и той же энергии электронов
и тяжелых частиц в нерелятивистском
случае удельные потери энергии
пропорциональны массе частиц.
Следовательно, для протонов они почти
в 2000 раз больше, чем для электронов. Это
очень важно для методов регистрации
частиц. Например, в ядерных эмульсиях
протоны с энергией 5 МэВ оставляют
отчетливый след, тогда как электрон
такой же энергии практически незаметен.
-
При очень высоких энергиях все по-другому.
При V~c член перед скобкой не меняется.
Становится существенной зависимость
от

под логарифмом. Поэтому при
ультрарелятивистских скоростях величина
dE/dx слабо зависит и от энергии, и от
массы
частицы. Например, при кинетической
энергии электрона и протона, равных 10
ГэВ потери энергии электронами в ≈ 2
раза превышают потери энергии протонами
(при различии их масс в 2000 раз).
Пробег заряженных частиц в веществе
Потеряв всю энергию, частица останавливается.
Расстояние, пройденное частицей в
веществе, называется пробегом. На этом
пути заряженная частица изменяет свою
энергию от начального значения E0 до
нуля в результате разных механизмов
взаимодействия, основным из
которых для области энергий до 100 МэВ
являются ионизационные потери. Поэтому
понятно, что величина пробега зависит
от массы, заряда, энергии частицы и
характеристик среды.
Пробег R частицы с начальной энергией
Е0 можно определить выражением

![]()
.
Подставим выражение для dE
для нерелятивистских частиц
![]()
а из формулы Бете-Блоха


Оценим теперь, как пробег зависит от параметров частицы и среды:

Выводы из этого соотношения:
1. При равных скоростях
пробеги частиц прямо пропорциональны
их массам и обратно
пропорциональны квадратам зарядов.
2. Пробеги обратно
пропорциональны плотности среды,
т.е. удобно измерять пробеги в массовых
единицах длины. В этом случае величина
пробега практически не будет зависеть
от характеристик среды:
![]()
При более аккуратных расчетах не следует
забывать, что в формуле Бете-Блоха есть
еще коэффициенты, зависящие от среды:
Z/A и I. Но для большинства веществ
с малыми и средними A величина отношения
Z/A~0,5 и очень медленно падает с
увеличением A, а средний ионизационный
потенциал I стоит под знаком логарифма,
т.е. тоже слабо влияет на величину средних
потерь энергии и, как следствие этого,
на величину пробега.
3.Чтобы сравнивать пробеги частиц с
одинаковыми кинетическими энергиями,
удобно несколько преобразовать выражение
для R:
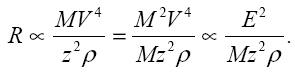
Из этого соотношения видно, что
при равных кинетических энергиях пробеги
частиц обратно пропорциональны их
массам. Этот факт проиллюстрирован
на Рис.

Рис. Ионизационные потери
Пробеги заряженных
заряженных частиц в кремнии
частиц в кремнии
Для сравнения рядом приведены графики
ионизационных потерь.

Траектории протонов в свинце.
Для практических целей
Для зависимостей R(Е) на основе обобщения
экспериментальных данных и расчетов
построены подробные таблицы и предложен
ряд интерполяционных формул. На практике
для оценок значений пробегов заряженных
частиц используют приближенные
эмпирические соотношения, справедливые
в определенных интервалах энергии, вида
![]()
,
где
![]()
пробег частицы с начальной энергией
Е0,
– эмпирический показатель степени
порядка 1.5.
В таблице представлены
коэффициенты аппроксимации для
заряженных частиц в кремнии.
|
Коэффициент |
р |
-частица |
С |
Si |
Fe |
|
REo, Е0, |
14.1 1.72 1 |
14.0 1.722 1 |
5.47 1.69 12 |
3.7 1.6 28 |
3.67 1.51 56 |
Заполняем
таблицу Пробег, R(E),
Е (МэВ)
|
протон |
-частица |
Si 1428 |
Fe5626 |
|
|
Энергия E = 1 МэВ |
||||
|
Энергия E = 10 МэВ |
||||
|
Энергия E |
||||
|
Энергия E |
||||
|
Энергия E |
Интересно отметить, что из эмпирической
зависимости, связывающей пробеги и
энергию ядерной частицы, можно получить
также оценку величины ионизационных
потерь:
![]()
В качестве примера на Рис. в. Представлены
рассчитанные с помощью этого соотношения
линейных потерь энергии при тех же
условиях, что и для данных, представленных
на Рис. а.

Рис. а. Ионизационные
потери Рис.б. Оценка линейных
потерь энергии
заряженных частиц
в кремнии в кремнии через
эмпирические зависимости
пробегов от энергии
Сравнение результатов показывает, что
эмпирические соотношения дают очень
большую погрешность при относительно
малых энергиях и для относительно
тяжелых ионов, поэтому пользоваться
этими соотношениями можно только для
относительно легких частиц и в области,
где имеется монотонно-убывающая
зависимость ЛПЭ от энергии частицы.
Рассматриваем
пробеги альфа-частиц в воздухе.
Средний пробег R
в воздухе при комнатной температуре и
нормальном давлении для альфа-частиц,
испускаемых естественным изотопом,
связан с энергией T
(в МэВ) эмпирической формулой
R
(см) = 0.32
(T)3/2
Пробеги
альфа-частиц (см)
|
Вещество |
Е |
Е |
Е |
Е |
|
Воздух |
2.5 |
4.6 |
7.4 |
10.6 |
|
Биоткань |
3.110-3 |
5.610-3 |
9.610-3 |
13.010-3 |
|
Алюминий |
1.610-3 |
3.010-3 |
4.810-3 |
6.910-3 |
Пусть на слой
поглотителя перпендикулярно к нему
падает пучок однородных частиц с
одинаковой энергией E0.
Как будет выглядеть зависимость числа
этих частиц N от толщины поглотителя x?
С
хематическое
представление поведения траекторий
первоначально параллельного пучка
нерелятивистских частиц в веществе. а
– альфа-частицы, б – электроны.
Характер движения
электронов через вещество существенно
иной, чем в случае тяжелых заряженных
частиц. Траектория электронов прямолинейна
только в начале пути. Среднеквадратичный
угол многократного рассеяния нарастает
как <θ2>1/2
~ x
1/2.
После большого числа актов рассеяния
уже нельзя говорить о преимущественном
направлении скоростей электронов –
наступает режим диффузии. Наконец, в
результате потерь энергии происходит
полная остановка.
Для тяжелых
заряженных частиц (практически всех
частиц, кроме электронов), которые
проходят слой поглотителя почти без
рассеяния и поэтому имеют прямолинейную
траекторию в веществе, все очень просто:
частицы выбывают из пучка в основном
из-за остановки в результате потерь
энергии на ионизацию и возбуждение
среды. А так как у них начальная энергия
E0 была
одинакова и средние потери энергии
dE/dx тоже одинаковы, то все частицы должны
были бы проходить одинаковые расстояния
в веществе. В этом случае кривая поглощения
должна описываться горизонтальной
резко обрывающейся линией. На самом
деле, вместо этой картины
наблюдается разброс
величины пробегов, связанный со
статистическим характером процесса
ионизационных потерь. Частицы теряют
свою энергию в очень большом, но конечном
числе отдельных актов. Флуктуациям
подвержено как число таких актов на
единицу длины, так и потери энергии в
каждом отдельном акте, в особенности в
связи с образованием δ-электронов.
Пробеги отдельных частиц распределены
около среднего пробега по закону Гаусса
![]()
,
где
![]()
– средний пробег,
![]()
–
среднеквадратичное отклонение от
среднего значения

Относительный разброс пробегов
![]()
называется стрэгглингом. Наличие этого
разброса приводит к тому, что кривая
поглощения имеет не резкий, а плавный
спад, такой, как изображен на рис. (для
α-частиц).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
