Задачи на движение по реке
Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.
Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.
Задача 1. Катер движется против течения реки. За сколько часов он преодолеет расстояние 112 км, если его собственная скорость 30 км/ч, а скорость течения реки 2 км/ч?
Решение: Сначала узнаем скорость движения катера против течения реки, для этого от его собственной скорости отнимем скорость течения:
30 – 2 = 28 (км/ч) — скорость движения катера против течения.
Теперь можно узнать за сколько часов катер преодолеет 112 км, разделив расстояние на скорость:
112 : 28 = 4 (ч).
Решение задачи по действиям можно записать так:
1) 30 – 2 = 28 (км/ч) — скорость движения катера против течения,
2) 112 : 28 = 4 (ч).
Ответ: За 4 часа катер преодолеет расстояние 112 км.
Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки.
Задача 2. Расстояние от пункта A до пункта B по реке равно 120 км. Сколько времени потратит моторная лодка на путь от пункта A до B, если её собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?
Рассмотрите два варианта:
1) лодка движется по течению реки;
2) лодка движется против течения реки.
Решение: Если моторная лодка будет двигаться по течению реки, то её скорость будет равна сумме собственной скорости со скоростью течения реки:
27 + 3 = 30 (км/ч).
Значит расстояние между пунктами лодка преодолеет за:
120 : 30 = 4 (ч).
Если лодка будет двигаться против течения реки, то её скорость будет равна разности собственной скорости и скорости течения реки:
27 – 3 = 24 (км/ч).
Значит, чтобы узнать сколько времени потратит лодка на путь от пункта A до пункта B, надо расстояние разделить на скорость:
120 : 24 = 5 (ч).
Решение задачи по действиям для движения по течению реки можно записать так:
1) 27 + 3 = 30 (км/ч) — скорость лодки,
2) 120 : 30 = 4 (ч).
Для движения против течения реки решение задачи по действиям можно записать так:
1) 27 – 3 = 24 (км/ч) — скорость лодки,
2) 120 : 24 = 5 (ч).
Ответ:
1) При движении по течению реки моторная лодка потратит 4 часа на путь от пункта A до пункта B.
2) При движении против течения реки моторная лодка потратит 5 часов на путь от пункта A до пункта B.
Рассказываем, как решать задачи на движение по реке. Приводим алгоритм решения и примеры. Задачи для самостоятельного решения.
Суть задач на движение по реке
Задачи на движение по реке – задачи на нахождение скорости, времени и расстояния при движении на реке.
Помни!
В решении задач на движение по реке используются те пункты алгоритма, в которых описано нахождение неизвестной величины (по условию задачи).
Алгоритм решения задач
Алгоритм решения задач на движение по воде:
- Выполняем краткую запись задачи;
- Выбираем способ решения и решаем задачу;
- Выписываем полный ответ.
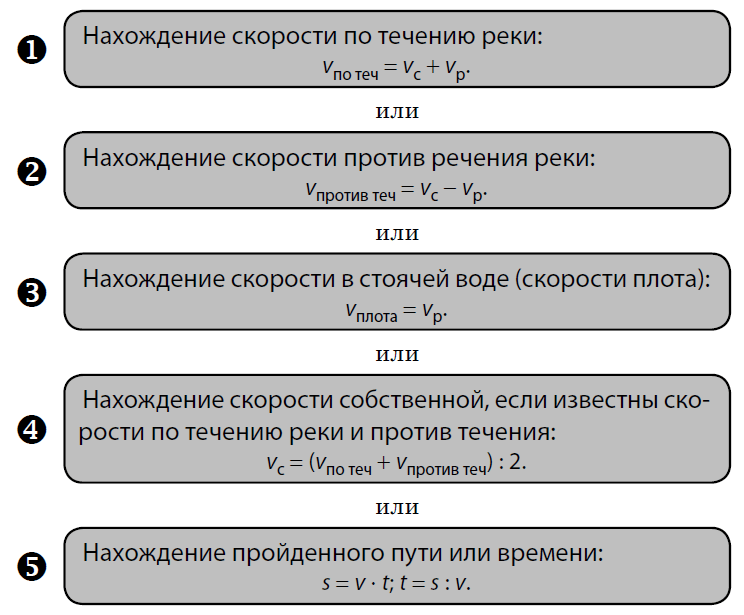
Выбираем способ решения:
![]()
Условные обозначения:

Способы решения задач
Примеры решения задачи
Базовые знания:
Задача 1. Катер прошел 54 км по течению реки и потратил на это 3 ч. Найти скорость течения реки, если собственная скорость катера 16 км/ч.
Краткая запись:

Решение:
1-й способ (арифметический)
- (54:3=18) (км/ч) — скорость по течению;
- (18-16=2) (км/ч) — скорость течения реки.
2-й способ (алгебраический)
- Пусть x км/ч — скорость течения реки, тогда (16 + x) км/ч — скорость катера по течению.
- Так как за 3 часа катер по течению прошел 54 км, составим и решим уравнение:
(3⋅(16+x)=54)
(16+x=54:3)
(16+x=18)
(x=18-16)
(x=2)
Ответ: скорость течения реки равна 2 км/ч.
Задачи для самостоятельного решения
- Расстояние между двумя пристанями 64 км. Скорость течения реки 4 км/ч. Собственная скорость катера равна 12 км/ч. За какое время катер пройдет от одной пристани
до другой по течению реки? - Расстояние между двумя пристанями 64 км. Собственная скорость катера равна 12 км/ч. За какое время катер пройдет расстояние между пристанями против течения реки,
если скорость течения реки 4 км/ч? - Катер курсирует между двумя городами по реке, скорость течения которой равна 6 км/ч. Какое время затратит катет на один рейс туда и обратно, если его собственная скорость 18 км/ч, а расстояние между пристанями — 48 км?
- Моторная лодка преодолевает расстояние 72 км по течению реки за 6 ч, а против течения — за 9 ч. Найти скорость течения реки и собственную скорость лодки.
Посмотреть еще в категории: Задачи по математике 5-6 класс
- Задачи на сложение и вычитание
- Задачи на движение навстречу друг другу
- Задачи на движение в одном направлении
- Задачи на движение в противоположных направлениях
- Задачи на нахождение дроби от числа
- Задачи на нахождение числа по его дроби
- Задачи на нахождение процента от числа
- Задачи на нахождение числа по его процентам
- Задачи на процентное отношение двух чисел
- Задачи на проценты (с помощью пропорции)
- Задачи на нахождение градусной меры угла
- Задачи на нахождение периметра и площади треугольника
- Задачи с использованием формул площадей прямоугольника и квадрата
- Задачи на нахождение объема прямоугольного параллелепипеда и куба
- Задачи на проценты
- Задачи на нахождение длины окружности и площади круга
Данный материал представляет собой систему
задач по теме “Движение”.
Цель: помочь учащимся более полно овладеть
технологиями решения задач по данной теме.
Задачи на движение по воде.
Очень часто человеку приходится совершать
движения по воде: реке, озеру, морю.
Сначала он это делал сам, потом появились плоты,
лодки, парусные корабли. С развитием техники
пароходы, теплоходы, атомоходы пришли на помощь
человеку. И всегда его интересовали длина пути и
время, затраченное на его преодоление.
Представим себе, что на улице весна. Солнце
растопило снег. Появились лужицы и побежали
ручьи. Сделаем два бумажных кораблика и пустим
один из них в лужу, а второй – в ручей. Что же
произойдет с каждым из корабликов?
В луже кораблик будет стоять на месте, а в
ручейке – поплывет, так как вода в нем “бежит”
к более низкому месту и несет его с собой. То же
самое будет происходить с плотом или лодкой.
В озере они будут стоять на месте, а в реке –
плыть.
Рассмотрим первый вариант: лужа и озеро. Вода в
них не движется и называется стоячей.
Кораблик поплывет по луже только в том случае,
если мы его подтолкнем или если подует ветер. А
лодка начнет двигаться в озере при помощи весел
или если она оснащена мотором, то есть за счет
своей скорости. Такое движение называют движением
в стоячей воде.
Отличается ли оно от движения по дороге? Ответ:
нет. А это значит, что мы с вами знаем как
действовать в этом случае.
Задача 1. Скорость катера по озеру равна 16 км/ч.
Какой путь пройдет катер за 3 часа?
Ответ: 48 км.
Следует запомнить, что скорость катера в
стоячей воде называют собственной скоростью.
Задача 2. Моторная лодка за 4 часа проплыла по
озеру 60 км.
Найдите собственную скорость моторной лодки.
Ответ: 15 км/ч.
Задача 3. Сколько времени потребуется лодке,
собственная скорость которой
равна 28 км/ч, чтобы проплыть по озеру 84 км?
Ответ: 3 часа.
Итак, чтобы найти длину пройденного пути,
необходимо скорость умножить на время.
Чтобы найти скорость, необходимо длину пути
разделить на время.
Чтобы найти время, необходимо длину пути
разделить на скорость.
Чем же отличается движение по озеру от
движения по реке?
Вспомним бумажный кораблик в ручье. Он плыл,
потому что вода в нем движется.
Такое движение называют движением по течению.
А в обратную сторону – движением против
течения.
Итак, вода в реке движется, а значит имеет свою
скорость. И называют ее скоростью течения реки.
( Как ее измерить?)
Задача 4. Скорость течения реки равна 2 км/ч. На
сколько километров река относит
любой предмет (щепку, плот, лодку) за 1час, за 4
часа?
Ответ: 2 км/ч, 8 км/ч.
Каждый из вас плавал в реке и помнит, что по
течению плыть гораздо легче, чем против течения.
Почему? Потому, что в одну сторону река
“помогает” плыть, а в другую – “мешает”.

Рис.1
Те же, кто не умеет плавать, могут представить
себе ситуацию, когда дует сильный ветер.
Рассмотрим два случая:
1) ветер дует в спину,
2) ветер дует в лицо.
И в том и в другом случае идти сложно. Ветер в
спину заставляет бежать, а значит, скорость
нашего движения увеличивается. Ветер в лицо
сбивает нас, притормаживает. Скорость при этом
уменьшается.
Остановимся на движении по течению реки. Мы уже
говорили о бумажном кораблике в весеннем ручье.
Вода понесет его вместе с собой. И лодка,
спущенная на воду, поплывет со скоростью течения.
Но если у нее есть собственная скорость, то она
поплывет еще быстрее.
Следовательно, чтобы найти скорость движения
по течению реки, необходимо сложить собственную
скорость лодки и скорость течения.
Задача 5. Собственная скорость катера равна 21
км/ч, а скорость течения реки 4 км/ч. Найдите
скорость катера по течению реки.
Ответ: 25км/ч.
Теперь представим себе, что лодка должна плыть
против течения реки. Без мотора или хотя бы весел,
течение отнесет ее в обратную сторону. Но, если
придать лодке собственную скорость ( завести
мотор или посадить гребца), течение будет
продолжать отталкивать ее назад и мешать
двигаться вперед со своей скоростью.
Поэтому, чтобы найти скорость лодки против
течения, необходимо из собственной скорости
вычесть скорость течения.
Задача 6. Скорость течения реки равна 3 км/ч, а
собственная скорость катера 17 км/ч.
Найдите скорость катера против течения.
Ответ: 14 км/ч.
Задача 7. Собственная скорость теплохода равна
47,2 км/ч, а скорость течения реки 4,7 км/ч. Найдите
скорость теплохода по течению и против течения.
Ответ: 51,9 км/ч; 42,5 км/ч.
Задача 8. Скорость моторной лодки по течению
равна12,4 км/ч. Найдите собственную скорость
лодки, если скорость течения реки 2,8 км/ч.
Ответ: 9,6 км/ч.
Задача 9. Скорость катера против течения равна
10,6 км/ч. Найдите собственную скорость катера и
скорость по течению, если скорость течения реки
2,7 км/ч.
Ответ: 13,3 км/ч; 16 км/ч.
Связь между скоростью по течению и
скоростью против течения.
Введем следующие обозначения:
Vс. – собственная скорость,
Vтеч. – скорость течения,
V по теч. – скорость по течению,
V пр.теч. – скорость против течения.
Тогда можно записать следующие формулы:
V no теч = Vc + Vтеч ;
V np. теч = Vc – V теч.;
Попытаемся изобразить это графически:
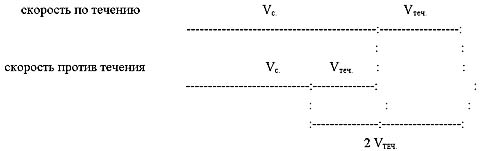
Рис. 2
Вывод: разность скоростей по течению
и против течения равна удвоенной скорости
течения.
Vno теч — Vnp. теч = 2 Vтеч.
Vтеч = (V по теч – Vnp. теч ): 2
Задача.
1) Скорость катера против течения равна 23 км/ч, а
скорость течения 4 км/ч.
Найдите скорость катера по течению.
Ответ: 31 км/ч.
2) Скорость моторной лодки по течению реки равна
14 км/ч/ а скорость течения 3 км/ч. Найдите скорость
лодки против течения
Ответ: 8 км/ч.
Задача 10. Определите скорости и заполните
таблицу:
|
V С. |
Vтеч. |
Vпо теч. |
Vпр.теч. |
|
|
1 |
12 км/ч |
3 км/ч |
||
|
2 |
23 км/ч |
25 км/ч |
||
|
3 |
24 км/ч |
20 км/ч |
||
|
4 |
4 км/ч |
17 км/ч: |
||
|
5 |
5 км/ч |
18 км/ч |
||
|
6 |
42 км/ч |
34 км/ч |
* – при решении п.6 смотри рис.2.
Ответ: 1) 15 и 9; 2) 2 и 21; 3) 4 и 28; 4) 13 и 9; 5)23 и 28; 6) 38 и 4.
Как найти расстояние против течения реки? Можно формулу пожалуйста
Карина
Ученик
(240),
на голосовании
7 лет назад
Голосование за лучший ответ
Галка
Просветленный
(25504)
7 лет назад
По течению реки скорость передвижения катера будет равна : скорость катера плюс скорость течения реки
А против течения реки скорость передвижения катера будет равна : скорость катера минус скорость течения реки
Расстояние вычисляем учитывая скорости с течением реки
Определение пройденного расстояния
Как уже было сказано
выше, пройденное судном расстояние
может быть определено с помощью
относительного или абсолютного лагов
или по скорости судна и времени плавания.
Определение пройденного расстояния с помощью относительного лага.
Относительные
лаги вырабатывают расстояния по
измеренной скорости с помощью интеграторов:

Для определения
пройденного расстояния относительно
воды (So)
со счётчика лага снимаются мгновенные
значения, называемые отсчётом
лага (ОЛ), в
начальный (ОЛ1)
и конечный (ОЛ2)
моменты плавания. Разность этих отсчетов
называется разностью
отсчетов лага
(РОЛ):
РОЛ = ОЛ2
ОЛ1
В показаниях лага,
как и каждого прибора, содержится
погрешность. Систематическая погрешность
лага компенсируется поправкой лага
(Л), имеющей обратный
знак. Л выражается
в процентах и представляет собой поправку
на относительную погрешность лага:
![]()
; (1.59)
![]()
, (1.60)
где
So – фактически пройденное судном
расстояние относительно воды, определяемое
различными точными навигационными
способами; Vo и Vл – скорости
судна относительно воды и показанная
лагом.
Зная Л
и введя её в показания лага, можно
получить пройденное расстояние
относительно воды, рассчитанное по
показаниям лага (Sл):
![]()
(1.61)
По этой формуле
составлена таблица 2.17 в
МТ – 2000,
реализующая формулу (1.59). Таблица
составлена для РОЛ до 100. Если РОЛ больше
100, то её разбивают на две части, каждая
из которых меньше 100 и для каждой части
выбирают Si
, которые
суммируют.
Пример:
Выбрать из таблицы 2.17 МТ – 2000 пройденное
расстояние Sл, если РОЛ = 123 и Л
=+6 %.
Для РОЛ
= 100
Sл
= 106,0 мили
+
Для РОЛ
= 23
Sл
= 24,4 мили
Р
ОЛ
= 123
Sл = 130,4 мили
Таблица составлена
для поправок лага до 10 %. Если Л
10 % , то её разбивают
на две части и выбирают расстояния по
каждой из этих составляющих поправки
лага, суммируют их и вычитают один РОЛ.
Пример:
Выбрать из таблицы 2.17 МТ – 2000 пройденное
расстояние Sл,
если
РОЛ = 75 и Л
= 13
%
Для Л
= 10
%
Sл
= 67,5 мили
+
Для Л
= -3% Sл
= 72,8 мили
![]()
Sл
= 140,3
Р
ОЛ
= 75,0
Для Л
=
13%Sл
= 65,3 мили
Вместо поправки
лага часто используют коэффициент
лага,
представляющий отношение расстояния
Sл
к разности отсчётов лага:
![]()
.
(1.62)
И тогда ![]()
(1.63)
Связь
между поправкой лага и коэффициентом
лага выражается формулами
![]()
,
(1.64)
![]()
.
(1.65)
Переход от Л
к Кл
и обратно очень прост. Например: Кл
= 1,09
Л
= +9%, Кл =
0,97
Л
= 3
%, Л
= +5 %
Кл
= 1,05, Л
=
11 %
Кл
= 0,89.
СКП расстояния,
пройденного относительно воды и
определяемого по относительному лагу
(в %), вычисляется по формуле
![]()
,
где
mРОЛ – СКП разности
отсчетов лага в %, определяемая
экспериментально для различных скоростей,
mЛ
– СКП поправки лага в %, определяемая
на мерной линии при определении скорости.
Ориентировочно
![]()
.
Недопустимо
определять пройденное расстояние по
показаниям относительной скорости по
лагу, т.к. скорость по шкале указателя
измеряется с большой погрешностью
![]()
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
