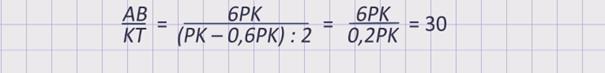Как найти расстояние против течения реки

Классическим примером текстовой задачи, которая может встретиться вам на ЕГЭ, является задача на движение. Эти задачи довольно разнообразны и включают в себя: задачи на движение навстречу, задачи на движение вдогонку, задачи на движение по реке. И поэтому вопрос, как же решать задачи на движение, иногда ставят учеников в тупик.

Научиться решать такие задачи довольно легко, для этого нужно знать алгоритм, состоящий всего из 3 шагов.

1. Формула, которую обязательно нужно знать, и секрет, как ее легко запомнить
2. Как решать задачи на движение: 3 простых шага
3. Задачи на движение вдогонку: примеры с решением
4. Задачи на движение навстречу: примеры с решением
5. Задачи на движение по течению и против течения: примеры с решением

Формула, которую обязательно нужно знать, и секрет, как ее легко запомнить

Для решения любой задачи на движение вам обязательно нужно знать всего одну формулу, которая вам уже давно известна:И уметь правильно выражать из этой формулы скорость и время:Многие ученики путаются при записи этих формул, допуская ошибки. Чтобы раз и навсегда запомнить формулы нахождения расстояния, скорости и времени, просто нарисуй треугольник. В верхнем углу треугольника напиши S, а внизу — V и t. Проведи горизонтальную черту между ними. Теперь мы можем закрыть рукой ту величину, которую нам нужно найти, и увидим формулу нахождения этой величины. Например, нам нужно найти расстояние. Закрываем рукой S, и на нашем рисунке останется V t – это и есть формула нахождения расстояния. Или нам нужно найти время. Закрываем рукой t, и на нашем рисунке остается  – формула нахождения времени. Нужно найти скорость? Закрываем рукой V, получаем  – формулу нахождения скорости. Главное запомнить, что S должна быть в верхнем углу. Это можно сделать, например, с помощью ассоциации, что S похожа на змею, а змея – хозяйка горы, поэтому она на вершине. Вот как выглядит такой магический треугольник:

Чтобы правильно решить задачу на движение нужно:

1. Определить неизвестное и составить таблицу на основании условия задачи.
2. Составить уравнение на основании таблицы.
3. Вернуться к условиям задачи и записать правильный ответ.

Давайте подробнее разберем каждый шаг:

1. Вначале нам нужно внимательно прочитать условие задачи и определить, что же взять за переменную Х. Чаще всего в задачах на движение удобнее всего за переменную Х обозначить скорость. Если же скорость нам прямо дана в условиях задачи, то за переменную Х обозначаем время. Если в условиях задачи прямо указаны значения и скорости, и времени, тогда за переменную Х берем расстояние. Затем из условий задачи определить все, что нам известно и занести в таблицу.
2. На основании полученной таблицы составляем уравнение и решаем его. После решения уравнения не торопимся записывать ответ. Ведь нахождение Х – это не всегда ответ к исходной задаче. Такую ошибку совершают многие ученики: фактически правильно решив задачу, они записывают неправильный ответ.
3. После решения уравнения возвращаемся к условиям задачи и смотрим, что же требовалось найти. Находим неизвестное и записываем ответ.

Задачи на движение бывают разными. В таких задачах участники движения могут двигаться навстречу друг другу, вдогонку, они могут двигаться по реке (против течения или по течению). Каждая из этих задач имеет особенности решения, о которых мы поговорим ниже и разберем на примерах.

Задачи на движение вдогонку: примеры с решением

При решении задачи, по условия которой оба участника движения двигаются в одном направлении, как правило, сравнивается время их движения. Необходимо запомнить правила:

1. Если время движения сравнивается (то есть присутствуют слова больше/меньше), то мы приравниваем время и прибавляем слагаемое. То есть чтобы получить большее время, мы прибавляем к меньшему времени что-то еще (из условий задачи).
2. Если условия задачи содержат общее время, то дроби, выражающее время, складываются.

Давайте разберем, как работают эти правила при решении задач.

Задача 1

Велосипедист и автомобилист одновременно выехали из пункта А в пункт Б, расстояние между которыми равно 50 км. Известно, что скорость автомобилиста на 40 км/ч больше, чем у велосипедиста, в результате чего автомобилист приехал в пункт Б на 4 часа раньше. Найдите скорость велосипедиста.

Решение:

1. Необходимо определить, что взять за переменную Х и составить таблицу. Вспоминаем, что удобнее всего за Х обозначить скорость в том случае, если она прямо не указано в условиях задачи.

В нашем случае скорость в условиях задачи не указана, поэтому скорость велосипедиста обозначаем за Х.

Составляем таблицу, данные для которой берем из условий задачи.

Итак, расстояние (S) нам известно – 50 км, скорость велосипедиста – х, скорость автомобилиста на 40 км/ч больше, значит она равна х + 40. Чтобы определить время вспоминаем формулу t = S / V и подставляем в нее наши значения. Время, затраченное велосипедистом, получится 50 / х, а время, затраченное автомобилистом — 50 / (х + 40).2. На основании таблицы и условий задачи необходимо составить уравнение.

Из условий задачи нам известно, что автомобилист приехал раньше велосипедиста на 4 часа (смотрим наше первое правило). Это значит, что велосипедист затратил на 4 часа больше времени, чем автомобилист. Следовательно,

50 / (х + 40) + 4 = 50 / х

Решаем полученное уравнение, для этого приводим наши дроби к одному знаменателю:

50х + 4х (х + 40) – 50 (х+40) / х (х + 40) = 0

(50х + 4х² + 160х – 50х – 2000) / х (х+40) = 0

(4х² + 160х – 2000) / (х² + 40х) = 0

Умножим обе части уравнение на х² + 40х:

4х² + 160х – 2000 = 0

Разделим обе части уравнения на 4:

х² + 40х – 500 = 0

Находим дискриминант:

D = 40² – 4 * 1 * (-500) = 3600

Далее находим корни уравнения:

х₁ = 10

х₂ = — 50

3. Возвращаемся к условиям задачи и вспоминаем, что же требовалось найти.

Нам нужно было определить скорость велосипедиста, которую мы обозначили за Х.

Скорость велосипедиста должна быть положительна, поэтому х₂ не подходит по смыслу задачи. Следовательно, нас интересует только х₁ и скорость велосипедиста равна 10 км/ч.

Ответ: 10 км/ч.

Задача 2

Велосипедист выехал с постоянной скоростью из города А в город Б, расстояние между которыми равно 80 км. На следующий день он поехал обратно, при этом его скорость была на 2 км/ч больше прежней. По пути велосипедист останавливался и отдыхал 2 часа. В итоге на возвращение из города Б в город А у него ушло времени столько же, сколько на путь из города А в город Б. Найдите скорость велосипедиста на пути из города А в город Б.

Решение:

1. Обозначим скорость велосипедиста на пути из города А в город Б как переменную Х.

Составим таблицу.

Из условий задачи: расстояние — 80 км, скорость велосипедиста во второй день – х. Его скорость во второй день была на 2 км/ч больше, чем в первый день, т.е. в первый день она была ниже, следовательно, скорость велосипедиста в первый день равна х – 2. Определим затраченное велосипедистом время на путь по формуле t = S / V. Тогда время, затраченное в первый день на путь равно 80 / х, во второй день — 80 / (х + 2).2. На основании таблицы и условий задачи составим уравнение.

Из условий задачи нам известно, что во второй день велосипедист останавливался и отдыхал 2 часа, следовательно, в пути он провел на 2 часа меньше (смотрим наше первое правило).  Также нам известно, что общее затраченное велосипедистом время в первый и во второй дни равно. Следовательно:

80 / (х + 2) + 2 =  (80 / х)

Решаем полученное уравнение, для чего приводим дроби к общему знаменателю:

(80х + 160 – 80х – 2х (х+2)) / х (х + 2) = 0

Умножаем обе части уравнения на х (х + 2):

160 – 2х² + 4х = 0

— 2х² — 4х + 160 = 0

Делим обе части уравнения на -2:

х² + 2х – 80 = 0

Находим дискриминант:

D = 2² – 4 * 1 * (-80) = 4 + 320 = 324

Тогда корни уравнения равны:

х₁ = 8

х₂ = — 10

3. Возвращаемся к условиям задачи. Нам необходимо было найти скорость велосипедиста на пути из города А в город Б, которую мы обозначали за Х.

Скорость должна быть положительна, поэтому х₂ = — 10 не подходит по смыслу задачи. Следовательно, скорость велосипедиста равна 8.

Ответ: 8 км/ч.

Задачи на движение навстречу: примеры с решением

Главное, что нужно помнить о движении навстречу: скорости участников движения складываются.

В тех случаях, когда нам неизвестно общее расстояние, то есть мы не можем его определить из условий задачи и из составленных уравнений, данное расстояние следует принимать за единицу.

Примеры решения задач на движение навстречу:

Задача 1

Из города А в город Б выехал автомобилист, через 3 часа навстречу ему выехал мотоциклист со скоростью 60 км/ч. Автомобилист и мотоциклист встретились на расстоянии 350 км от города А. Расстояние между городами А и Б равно 470 км. Найдите скорость автомобилиста.

Решение:

1. Обозначим скорость автомобилиста как Х.

Автомобилист и мотоциклист встретились на расстоянии 350 км от города А. Следовательно, автомобилист проехал 350 км, а мотоциклист 470 – 350 = 120 км.

Составим таблицу:2. Составим уравнении на основании таблицы и условий задачи.

Из условий задачи известно, что автомобилист ехал на 3 часа дольше, чем мотоциклист (пользуемся первым правилом, которое разбирали при решении задач на движение вдогонку). Следовательно:

350/х = 120/60 + 3

350/х = 5

Решаем полученное уравнение:

5х = 350

х = 70

3. Возвращаемся к условиям задачи. Нам необходимо было найти скорость автомобилиста, которую мы обозначали за Х. Следовательно, скорость автомобилиста равна 70 км/ч.

Ответ: 70 км/ч.

Задача 2

Из городов А и Б одновременно навстречу друг другу выехали автомобилист и велосипедист. Автомобилист приехал в город А на 6 часов раньше, чем велосипедист приехал в город Б. Встретились они через 4 часа после начала движения. Сколько времени затратил автомобилист на путь из города Б в город А?

Решение:

1. Время автомобилиста обозначим как Х.

Примем расстояние между городами А и Б за единицу. Остальные данные берем из условий задачи.

Составим таблицу:2. Составим уравнение на основании таблицы и условий задачи.

Известно, что велосипедист и автомобилист встретились через  4 часа после начала движения  и в сумме преодолели все расстояние от города А до города Б. То есть все расстояние от города А до города Б было преодолено за 4 часа.

Вспоминаем, что при движении навстречу скорости движения участников складываются. Подставим в формулу пути известные нам данные:

((1 / х) +  (1 / (х — 6))) * 4 = 1

Решаем полученное уравнение:

(4 / х) +  (4 / (х — 6)) = 1

Приводим дроби к одному знаменателю:

(4х — 24 + 4х — х² + 6х) / (х (х — 6))  = 0

Делим обе части уравнения на х (х — 6), при условии, что х > 6:

-х² + 14х — 24 = 0

Умножим обе части уравнение на -1:

х² — 14х + 24 = 0

Находим дискриминант нашего квадратного уравнения:

D = 14² – 4 * 1 * 24 = 100

Находим корни уравнения:

х₁ = 12

х₂ = 2

х₂ < 6, следовательно, корнем уравнения не является.

3. Возвращаемся к условиям задачи. Нам необходимо было определить, сколько времени затратил автомобилист на путь из города Б в город А. Это время мы обозначали за Х. Следовательно, автомобилист затратил на путь из города Б в город А 12 часов.

Ответ: 12 часов.

Задачи на движение по течению и против течения: примеры с решением

В условиях задач на движение по реке всегда дано две скорости: собственная скорость судна (скорость, с которой он может двигаться в неподвижной воде) и скорость течения.

При этом возможны две ситуации: когда судно движется по течению и когда судно движется против течения.

Когда судно движется по течению, то течение помогает судну двигаться, оно начинает двигаться быстрее, следовательно, собственная скорость судна и скорость течения складываются.

Когда же судно двигается против течения, то оно ощущает сопротивление, плыть ему становится тяжелее. В этом случае скорость течения будет вычитаться из собственной скорости судна.

Давайте рассмотрим примеры решения задач на движение по реке.

Задача 1

Катер прошел против течения реки 160 км/ч и вернулся в пункт отправления, затратив времени на обратный путь на 8 часов меньше. Найдите скорость катера в неподвижной воде, если известно, что скорость течения реки равна 5 км/ч.

Решение:

1. Обозначим собственную скорость катера – х.

Составим таблицу:2. На основании таблицы и условий задачи составим уравнение.

По условиям задачи известно, что время, затраченное на путь по течению реки, на 8 часов меньше, чем время, затраченное на путь против течения реки (пользуемся первым правилом, которое разбирали при решении задач на движение вдогонку). Соответственно:

160 / (х + 5) + 8 = 160 / (х — 5)

Решаем данное уравнение. Для этого приводим дроби к общему знаменателю:

(160 (х – 5) + 8 (х – 5) (х + 5) – 160 (х + 5)) / (х – 5) (х + 5) = 0

(160х – 800 + (8х – 40) (х + 5) – 160х — 800) / (х – 5) (х + 5)  = 0

Умножаем обе части уравнения на (х – 5) (х + 5):

-1600 + 8х² + 40х – 40х – 200 = 0

8х² – 1800 = 0

8х² = 1800

х² = 225

х_1,2 = ±15

3. Возвращаемся к условию задачи. Нам необходимо было найти собственную скорость катера, которую мы обозначили за Х. Так как скорость не может быть отрицательной, то х₁ = -15 противоречит условию задачи. Следовательно, собственная скорость катера равна 15 км/ч.

Ответ: 15 км/ч.

Задача 2

Моторная лодка вышла в 9:00 из пункта А в пункт Б, расстояние между которыми 30 км. Пробыв в пункте Б 3 часа, моторная лодка повернула назад и вернулась в пункт А в 20:00. Найдите скорость течения реки, если известно, что собственная скорость моторной лодки 8 км/ч.

Решение:

1. Обозначим скорость течения реки за х. Остальные данные берем из условия задачи.

Составим таблицу:2. Составим уравнение.

Нам известно, что моторная лодка начала свое движение в 9:00, а закончила в 20:00, а также в течение этого времени пробыла без движения во время стоянки – 3 часа. Таким образом, общее время движения будет 20 – 9 – 3 = 8 часов. Когда речь идет об общем времени движения, то нам нужно сложить время движения по течению и время движения против течения (пользуемся вторым правилом, которое разбирали при решении задач на движение вдогонку). Получаем:

30 / (8+х) + 30 / (8-х) = 8

Решаем полученное уравнение. Для этого приводим дроби к общему знаменателю:

(30 (8+х) + 30 (8-х) – 8 (8-х) (8+х)) / (8-х) (8+х) = 0

Умножаем обе части уравнения на (8-х) (8+х):

240 + 30х + 240 – 30х – (64 – 8х) (8+х) = 0

480 – 512 – 64х + 64х – 8х² = 0

8х² = 32

х² = 4

х_1,2 = ±2

3. Возвращаемся к условию задачи. Нам необходимо было найти скорость течения, которую мы обозначили за х. Так как скорость не может быть отрицательной, то х₁ = -2 противоречит условию задачи. Следовательно, скорость течения равна 2 км/ч.

Ответ: 2 км/ч.

Итак, мы разобрались, как решать задачи на движения. В ЕГЭ 2023 помимо задач на движение могут содержаться и другие текстовые задачи: на смеси и сплавы, на работу, на проценты. О том, как их решать, вы можете узнать на нашем сайте, а также .

Рассказываем, как решать задачи на движение по реке. Приводим алгоритм решения и примеры. Задачи для самостоятельного решения.

Суть задач на движение по реке

Алгоритм решения задач

Способы решения задач

Примеры решения задачи

Задачи для самостоятельного решения

Здравствуйте, дорогие читатели, подписчики и гости канала. Продолжаем разбор текстовых задач из ОГЭ 2021 года, входящие в 21 задание. Рассмотрим решение задач на движение по воде. В задачах за неизвестное (Х) будем брать то, что нужно найти.

Задача №1

Пусть Х – собственная скорость баржи. Если баржа плывет по течению реки, то ее собственная скорость увеличивается на скорость реки, и наоборот. Все данные из задачи перенесем в таблицу.

Так как весь путь по течению реки и против течения составил 5 часов, то составим уравнение:

Решим уравнение:

Задача №2

Пусть Х – скорость лодки в неподвижной воде. Тогда по течению реки будет Х+5, против течения реки Х-5.

Важно! Скорость течения реки равна 3 км/ч, с этой же скорость плывет плот, так как у плота нет своей скорости. Зная скорость плота и расстояние, которое плыл плот. Время, которое плыл плот равно: 33:3=11 часов.

Моторная лодка вышла вслед за плотом через один час, значит она плыла 10 часов. Составим уравнение:

Решим уравнение:

Задача №3

Пусть Х – скорость лодки в неподвижной воде. Тогда скорость лодки по течению будет равна Х+4, против течения Х-4. Внесем все данные в таблицу и найдем время движения лодки по течению и против течения реки.

Время движения против течения реки больше чем время движения по течению на 2 часа. Составим уравнение:

Решим уравнение, найдем скорость лодки в неподвижной воде:

Задача №4

Пусть Х – скорость течения реки. Тогда скорость теплохода по течению реки будет 25+х, против течения – 25-х.

Найдем, сколько времени был теплоход в пути. Теплоход вернулся в пункт отправления через 32 часа, а стоял в пункте назначения 21 час, значит в пути по воде в обе стороны теплоход плыл 32-21=11 часов.

Составим уравнение:

Решим уравнение и найдем скорость течения реки:

Спасибо, что дочитали. Вы меня очень поддержите, если поставите класс и подпишитесь на мой блог.

Путеводитель по каналу здесь

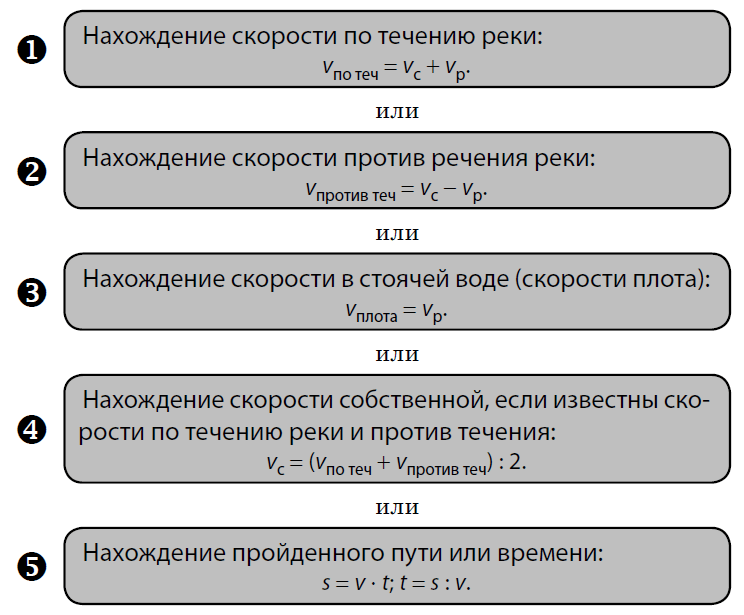
§ 1  Методика решения задач на движение по течению и против течения

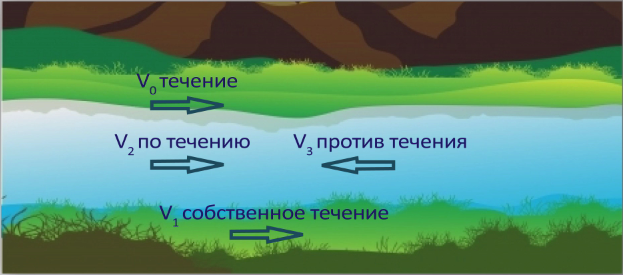
Из всех текстовых задач на движение особое место занимают задачи на движение по течению и против течения реки. Для успешного их решения необходимо различать 4 вида движения: течение реки, собственное движение, движение по течению и движение против течения реки.

Вид движения «течение реки» встречается в тех задачах, в которых рассматриваются движения немеханизированных объектов, например, движение плота. Такой вид движения возможен только по течению и скорость движущегося объекта всегда совпадает со скоростью течения реки.

Собственное движение характерно для механизированных объектов в стоячей воде, например, катер движется по озеру.

Движение по течению и движение против течения реки формируется из двух видов движения – собственного и течения реки.

При движении по течению направления течения реки и движения объекта совпадают, поэтому скорость перемещения тела при этом виде движения равна сумме собственной скорости тела и скорости течения

vсобств + vтечения.

При движении против течения течение реки препятствует движению объекта, поэтому скорость перемещения тела при этом виде движения равна разности собственной скорости тела и скорости течения

vсобств– vтечения.

Полезно знать, что сумма скоростей по течению и против течения реки равна удвоенной собственной скорости

vпо теч + vпротив теч = 2vсобств,

а разность этих скоростей равна удвоенной скорости течения реки

vпо теч – vпротив теч = 2vтечения.

Часто упрощает решение задач на движение понимание взаимной обратной зависимости скорости и времени движения: чем больше время, тем меньше скорость движения, и, наоборот, чем больше скорость движения, тем меньше времени тратится на прохождение пути.

В качестве неизвестных в таких текстовых задачах удобно выбирать расстояние и скорости движущихся тел, если они не заданы. В задачах, где в условии не представлены единицы длины, принято весь путь брать за единицу длины, а часть этого пути выражают долей всего пути без наименования.

В текстовых задачах на движение, связанных с течением реки, при проведении смысловой проверки полезно знать, что моторная лодка имеет собственную скорость12 – 40 км/ч, скорость течения реки изменяется в пределах 1 – 4км/ч, а скорость лодки на вёслах составляет примерно 3 – 8км/ч.

Рассмотрим приёмы решения текстовых задач на движение по течению и против течения на примерах решения следующих задач.

§ 2  Примеры решения задач на движение по течению и против течения

Задача 1.От пристани А до пристани В моторная лодка по течению реки проходит за 6 часов, а возвращается за 10 часов. За сколько часов пройдёт расстояние от А до В плот?

РЕШЕНИЕ.Решим задачу арифметическим способом.

Мы знаем, что расстояние определяется по формуле S = vt, где v– скорость лодки, t– время движения лодки, выраженное в часах. В задаче не используются единицы длины, значит, расстояние от А до В обозначим за единицу 1.

По условию задачи моторная лодка по течению реки проходит за 6 часов, значит, скорость по течению реки равна 1 : 6.

Моторная лодка возвращается за 10 часов, значит, расстояние АВ против течения реки лодка проходит за 10 часов, следовательно, её скорость при таком движении равна одной десятой. Для того, чтобы найти время движения плота на дистанции АВ, надо найти скорость плота, которая совпадает со скоростью течения реки. Известно, что удвоенная скорость течения реки равна разности скоростей по течению и против течения, то есть 

2vтечения = vпо теч – vпротив теч.

Вычислив разность скоростей по течению и против течения реки, имеем

Таким образом, решив уравнение

получаем, что скорость течения реки

Получили, что за 1 час плот проплывёт одну тридцатую всего пути от пункта А до пункта В.

Чтобы найти время движения плота, надо путь 1 единицу разделить на скорость его движения.

Получили, что плот пройдёт расстояние от А до В за 30часов.

Ответ: 30 часов.

А теперь рассмотрим алгебраический способ решения данной задачи. введём переменные пусть х км/ч – собственная скорость моторной лодки, у км/ч – скорость течения реки.

Cоставим таблицу данных с введёнными переменными.

Обозначим в столбцах таблицы элементы движения:

v– скорость, выраженная в км/ч,

t– время, выраженное в часах,

S– расстояние, выраженное в км.

В строках – виды движения: собственное движение, течение, движение по течению, движение против течения. Заметим, что движение течения и движение плота – это идентичные виды движения. Заполним таблицу согласно условий задачи.

В собственном виде движения мы ввели скорость движения лодки х км/ч, внесём её в соответствующую ячейку таблицы, в ячейках t и S поставим прочерк, так как эти данные не используются в данной задаче. В движении плота мы ввели скорость течения реки у км/ч, внесём в таблицу, а ячейки t и S заполним позже.

В движении по течению реки выразим скорость v суммой скоростей лодки и течения, то есть х + у км/ч, время t по условию задачи равно 6ч, значит, можем выразить расстояние от пункта А до пункта В. Оно равно 6(х + у)км.

В движении против течения реки выразим скорость vразностью скоростей лодки и течения, то есть х – у км/ч, время t по условию задачи равно 10ч, значит, можем выразить расстояние от пункта А до пункта В. Оно равно 10(х – у)км.

В движениях по течению и против течения реки расстояния равны между собой, значит, можем составить уравнение 6(х + у) = 10(х – у).

Дополним строку движения плота: расстояние S будет равно расстоянию движения по течению или против течения, значит, можем вписать выражение 6(х + у) км или 10(х – у) км.

Теперь можем выразить время движения плота

Или

Из уравнения 6(х + у) = 10(х – у) выразим одну переменную через другую, например, переменную х через у.

Имеем, 6х + 6у = 10х – 10у.

Отсюда получаем 4х = 16у, следовательно, х = 4у.

Подставим 4у вместо х в одно из выражений времени движения плота, имеем

Мы ответили на главный вопрос задачи: за 30 часов плот пройдёт расстояние от А до В.

Решим эту же задачу графическим способом.

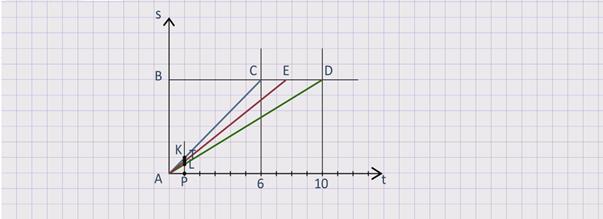
Зададим координатную плоскость: по горизонтальной оси абсцисс будем отмечать время движения, по вертикальной оси ординат отметим расстояние АВ. По течению реки лодка прошла 6 часов, значит, изобразим движение лодки синим отрезком АС с концами в точках А(0; 0) и С(6; АВ).

Против течения реки лодка прошла 10 часов, значит, изобразим движение лодки зелёным отрезком АD с концами в точках A(0; 0) и D(10; АВ). Рассмотрим на синей и зелёной линиях точки с абсциссой 1 и отметим их точками K и L соответственно. Точку на оси абсцисс с абсциссой 1 обозначим буквой Р. Таким образом, отрезок РК моделирует скорость движения лодки по течению, PL моделирует скорость движения лодки против течения.

Так как собственная скорость лодки есть среднее арифметическое между скоростями по течению и против течения реки, то линия собственного движения будет расположена между синей и зелёной линиями и будет являться медианой треугольника, образованного этими линиями и прямой х = 1. Обозначим середину отрезка КL точкой Т. Отрезок РТ моделирует собственную скорость движения лодки, Чтобы ответить на главный вопрос задачи, надо расстояние АВ поделить на скорость течения реки. Эта скорость моделируется на графикеравными отрезками КТ и ТL. Отрезки будут равны, так как они отражают разность скоростей по течению и собственной или разность скоростей собственной и против течения.

Отметим красным цветом отрезок АЕ с концами в точке А(0;0) и точке Е – точкой пересечения луча АЕ с прямой у = АВ, лежащий на отрезке АТ. Таким образом, время движения плота равно отношению длины отрезка АВ к длине отрезка КТ или АВ к длине отрезка TL, то есть

Чтобы найти длину отрезка KТ, надо найти полуразность скоростей по течению и против течения реки, а значит, полуразность длин отрезков РК и РL, то есть (РК – PL) : 2.

Так как АВ = 6РК = 10PL, то PL = 0,6PK. Имеем,

Получили, что плот пройдёт расстояние АВ за 30 часов.

Таким образом, на этом занятии мы решили одну и ту же задачу тремя различными способами и увидели, что ответ на главный вопрос задачи не зависит от способа её решения. Во всех трёх случаях мы получили один и тот же ответ.