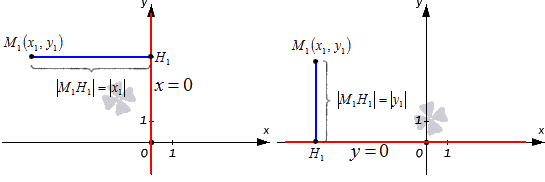Как найти расстояние прямой от начала координат - Сайт, где вы сможете решить свои вопросы

Данная статья рассказывает о теме «расстояния от точки до прямой», рассматриваются определения расстояния от точки к прямой с иллюстрированными примерами методом координат. Каждый блок теории в конце имеет показанные примеры решения подобных задач.

Расстояние от точки до прямой – определение

Расстояние от точки до прямой находится через определение расстояния от точки до точки. Рассмотрим подробней.

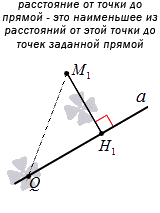
Пусть имеется прямая a и точка М1, не принадлежащая заданной прямой. Через нее проведем прямую b, расположенную перпендикулярно относительно прямой a. Точка пересечения прямых возьмем за Н1. Получим, что М1Н1 является перпендикуляром, который опустили из точки М1 к прямой a.

Определение 1

Расстоянием от точки М1 к прямой a называется расстояние между точками М1 и Н1.

Бывают записи определения с фигурированием длины перпендикуляра.

Определение 2

Расстоянием от точки до прямой называют длину перпендикуляра, проведенного из данной точки к данной прямой.

Определения эквивалентны. Рассмотрим рисунок, приведенный ниже.

Известно, что расстояние от точки до прямой является наименьшим из всех возможных. Рассмотрим это на примере.

Если взять точку Q, лежащую на прямой a, не совпадающую с точкой М1, тогда получим, что отрезок М1Q называется наклонной, опущенной из М1 к прямой a. Необходимо обозначить, что перпендикуляр из точки М1 является меньше, чем любая другая наклонная, проведенная из точки к прямой.

Чтобы доказать это, рассмотрим треугольник М1Q1Н1, где М1Q1 является гипотенузой. Известно, что ее длина всегда больше длины любого из катетов. Значим, имеем, что M1H1<M1Q. Рассмотрим рисунок, приведенный ниже.

Расстояние от точки до прямой на плоскости – теория, примеры, решения

Исходные данные для нахождения от точки до прямой позволяют использовать несколько методов решения: через теорему Пифагора, определения синуса, косинуса, тангенса угла и другими. Большинство заданий такого типа решают в школе на уроках геометрии.

Когда при нахождении расстояния от точки до прямой можно ввести прямоугольную систему координат, то применяют метод координат. В данном пункте рассмотрим основных два метода нахождения искомого расстояния от заданной точки.

Первый способ подразумевает поиск расстояния как перпендикуляра, проведенного из М1 к прямой a. Во втором способе используется нормальное уравнение прямой а для нахождения искомого расстояния.

Если на плоскости имеется точка с координатами M1(x1, y1), расположенная в прямоугольной системе координат, прямая a, а необходимо найти расстояние M1H1, можно произвести вычисление двумя способами. Рассмотрим их.

Первый способ

Если имеются координаты точки H1, равные x2, y2, тогда расстояние от точки до прямой вычисляется по координатам из формулы M1H1=(x2-x1)2+(y2-y1)2.

Теперь перейдем к нахождению координат точки Н1.

Известно, что прямая линия в Оху соответствует уравнению прямой на плоскости. Возьмем способ задания прямой a через написание общего уравнения прямой или уравнения с угловым коэффициентом. Составляем уравнение прямой, которая проходит через точку М1 перпендикулярно заданной прямой a. Прямую обозначим буковой b. Н1 является точкой пересечения прямых a и b, значит для определения координат необходимо воспользоваться статьей, в которой идет речь о координатах точек пересечения двух прямых.

Видно, что алгоритм нахождения расстояния от заданной точки M1(x1, y1) до прямой a проводится согласно пунктам:

Определение 3

нахождение общего уравнения прямой a, имеющее вид A1x+B1y+C1=0 ,или уравнение с угловым коэффициентом, имеющее вид y=k1x+b1;
получение общего уравнения прямой b, имеющее вид A2x+B2y+C2=0 или уравнение с угловым коэффициентом y=k2x+b2, если прямая b пересекает точку М1 и является перпендикулярной к заданной прямой a;
определение координат x2, y2 точки Н1_,являющейся точкой пересечения a и b, для этого производится решение системы линейных уравнений A1x+B1y+C1=0A2x+B2y+C2=0 или y=k1x+b1y=k2x+b2;
вычисление искомого расстояния от точки до прямой, используя формулу M1H1=(x2-x1)2+(y2-y1)2.

Второй способ

Теорема способна помочь ответить на вопрос о нахождении расстояния от заданной точки до заданной прямой на плоскости.

Теорема

Прямоугольная система координат имеет Оху имеет точку M1(x1, y1), из которой проведена прямая а к плоскости, задаваемая нормальным уравнением плоскости, имеющее вид cos α·x+cos β·y-p=0, равно по модулю значению, получаемому в левой части нормального уравнения прямой, вычисляемому при x=x1, y=y1, значит, что M1H1=cos α·x1+cos β·y1-p.

Доказательство

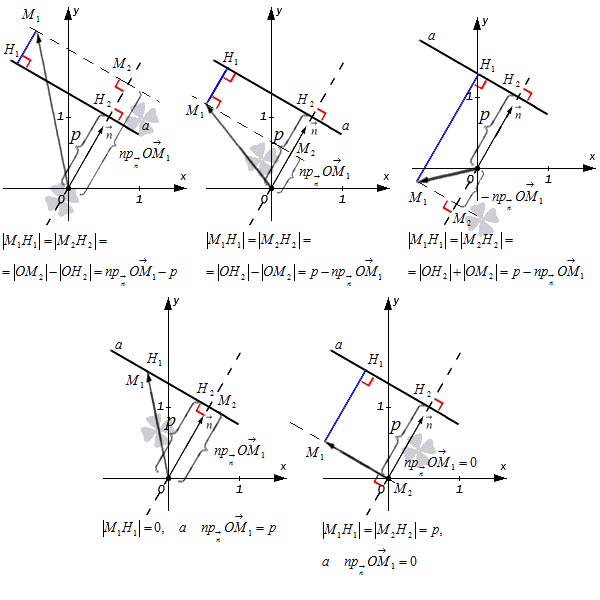
Прямой а соответствует нормальное уравнение плоскости, имеющее вид cos α·x+cos β·y-p=0, тогда n→=(cos α, cos β) считается нормальным вектором прямой a при расстоянии от начала координат до прямой a с p единицами. Необходимо изобразить все данные на рисунке, добавить точку с координатами M1(x1, y1), где радиус-вектор точки М1 – OM1→=(x1, y1). Необходимо провести прямую от точки до прямой, которое обозначим M1H1. Необходимо показать проекции М2 и Н2 точек М1 и Н2 на прямую, проходящую через точку O с направляющим вектором вида n→=(cos α, cos β), а числовую проекцию вектора обозначим как OM1→=(x1, y1) к направлению n→=(cos α, cos β) как npn→OM1→.

Вариации зависят от расположения самой точки М1. Рассмотрим на рисунке, приведенном ниже.

Результаты фиксируем при помощи формулы M1H1=npn→OM→1-p. После чего приводим равенство к такому виду M1H1=cos α·x1+cos β·y1-p для того, чтобы получить npn→OM→1=cos α·x1+cos β·y1.

Скалярное произведение векторов в результате дает преобразованную формулу вида n→, OM→1=n→·npn→OM1→=1·npn→OM1→=npn→OM1→, которая является произведением в координатной форме вида n→, OM1→=cos α·x1+cos β·y1. Значит, получаем, что npn→OM1→=cos α·x1+cos β·y1. Отсюда следует, что M1H1=npn→OM1→-p=cos α·x1+cos β·y1-p. Теорема доказана.

Получаем, что для нахождения расстояния от точки M1(x1, y1) к прямой a на плоскости необходимо выполнить несколько действий:

Определение 4

получение нормального уравнения прямой a cos α·x+cos β·y-p=0, при условии, что его нет в задании;
вычисление выраженияcos α·x1+cos β·y1-p, где полученное значение принимает M1H1.

Решение задач на нахождение расстояния от заданной точки до заданной прямой на плоскости

Применим данные методы на решении задач с нахождением расстояния от точки до плоскости.

Пример 1

Найти расстояние от точки с координатами M1(-1, 2) к прямой 4x-3y+35=0.

Решение

Применим первый способ для решения.

Для этого необходимо найти общее уравнение прямой b, которая проходит через заданную точку M1(-1, 2), перпендикулярно прямой 4x-3y+35=0. Из условия видно, что прямая b является перпендикулярной прямой a, тогда ее направляющий вектор имеет координаты, равные(4, -3). Таким образом имеем возможность записать каноническое уравнение прямой b на плоскости, так как имеются координаты точки М1, принадлежит прямой b. Определим координаты направляющего вектора прямой b. Получим, что x-(-1)4=y-2-3⇔x+14=y-2-3. Полученное каноническое уравнение необходимо преобразовать к общему. Тогда получаем, что

x+14=y-2-3⇔-3·(x+1)=4·(y-2)⇔3x+4y-5=0

Произведем нахождение координат точек пересечения прямых, которое примем за обозначение Н1. Преобразования выглядят таким образом:

4x-3y+35=03x+4y-5=0⇔x=34y-3543x+4y-5=0⇔x=34y-3543·34y-354+4y-5=0⇔⇔x=34y-354y=5⇔x=34·5-354y=5⇔x=-5y=5

Из выше написанного имеем, что координаты точки Н1равны (-5;5).

Необходимо вычислить расстояние от точки М1 к прямой a. Имеем, что координаты точек M1(-1, 2) и H1(-5, 5), тогда подставляем в формулу для нахождения расстояния и получаем, что

M1H1=(-5-(-1)2+(5-2)2=25=5

Второй способ решения.

Для того, чтобы решить другим способом, необходимо получить нормальное уравнение прямой. Вычисляем значение нормирующего множителя и умножаем обе части уравнения 4x-3y+35=0. Отсюда получим, что нормирующий множитель равен -142+(-3)2=-15, а нормальное уравнение будет вида -15·4x-3y+35=-15·0⇔-45x+35y-7=0.

По алгоритму вычисления необходимо получить нормальное уравнение прямой и вычислить его со значениями x=-1, y=2. Тогда получаем, что

-45·-1+35·2-7=-5

Отсюда получаем, что расстояние от точки M1(-1, 2) к заданной прямой 4x-3y+35=0 имеет значение -5=5.

Ответ: 5.

Видно, что в данном методе важно использование нормального уравнения прямой, так как такой способ является наиболее коротким. Но первый метод удобен тем, что последователен и логичен, хотя имеет больше пунктов вычисления.

Пример 2

На плоскости имеется прямоугольная система координат Оху с точкой M1(8, 0) и прямой y=12x+1. Найти расстояние от заданной точки до прямой.

Решение

Решение первым способом подразумевает приведение заданного уравнения с угловым коэффициентом к уравнению общего вида. Для упрощения можно сделать иначе.

Если произведение угловых коэффициентов перпендикулярных прямых имеют значение -1, значит угловой коэффициент прямой перпендикулярной заданной y=12x+1 имеет значение 2. Теперь получим уравнение прямой, проходящее через точку с координатами M1(8, 0). Имеем, что y-0=-2·(x-8)⇔y=-2x+16.

Переходим к нахождению координат точки Н1, то есть точкам пересечения y=-2x+16 и y=12x+1. Составляем систему уравнений и получаем:

y=12x+1y=-2x+16⇔y=12x+112x+1=-2x+16⇔y=12x+1x=6⇔⇔y=12·6+1x=6=y=4x=6⇒H1(6, 4)

Отсюда следует, что расстояние от точки с координатами M1(8, 0) к прямой y=12x+1 равно расстоянию от точки начала и точки конца с координатами M1(8, 0) и H1(6, 4). Вычислим и получим, что M1H1=6-82+(4-0)220=25.

Решение вторым способом заключается в переходе от уравнения с коэффициентом к нормальному его виду. То есть получим y=12x+1⇔12x-y+1=0, тогда значение нормирующего множителя будет -1122+(-1)2=-25. Отсюда следует, что нормальное уравнение прямой принимает вид -25·12x-y+1=-25·0⇔-15x+25y-25=0. Произведем вычисление от точки M18, 0 к прямой вида -15x+25y-25=0. Получаем:

M1H1=-15·8+25·0-25=-105=25

Ответ: 25.

Пример 3

Необходимо вычислить расстояние от точки с координатами M1(-2, 4) к прямым 2x-3=0 и y+1=0.

Решение

Получаем уравнение нормального вида прямой 2x-3=0:

2x-3=0⇔12·2x-3=12·0⇔x-32=0

После чего переходим к вычислению расстояния от точки M1-2, 4 к прямой x-32=0. Получаем:

M1H1=-2-32=312

Уравнение прямой y+1=0 имеет нормирующий множитель со значением равным -1. Это означает, что уравнение примет вид -y-1=0. Переходим к вычислению расстояния от точки M1(-2, 4) к прямой -y-1=0. Получим, что оно равняется -4-1=5.

Ответ: 312 и 5.

Подробно рассмотрим нахождение расстояния от заданной точки плоскости к координатным осям Ох и Оу.

В прямоугольной системе координат у оси Оу имеется уравнение прямой, которое является неполным имеет вида х=0, а Ох – y=0. Уравнения являются нормальными для осей координат, тогда необходимо найти расстояние от точки с координатами M1x1, y1 до прямых. Это производится, исходя из формул M1H1=x1 и M1H1=y1. Рассмотрим на рисунке, приведенном ниже.

Пример 4

Найти расстояние от точки M1(6, -7) до координатных прямых, расположенных в плоскости Оху.

Решение

Так как уравнение у=0 относится к прямой Ох, можно найти расстояние от M1 с заданными координатами, до этой прямой, используя формулу. Получаем, что 6=6.

Так как уравнение х=0 относится к прямой Оу, то можно найти расстояние от М1 к этой прямой по формуле. Тогда получим, что -7=7.

Ответ: расстояние от М1к Ох имеет значение 6, а от М1к Оу имеет значение 7.

Расстояние от точки до прямой в пространстве – теория, примеры, решения

Когда в трехмерном пространстве имеем точку с координатами M1(x1, y1, z1), необходимо найти расстояние от точки A до прямой a.

Рассмотрим два способа, которые позволяют производить вычисление расстояние от точки до прямой a, расположенной в пространстве. Первый случай рассматривает расстояние от точки М1 к прямой, где точка на прямой называется Н1 и является основанием перпендикуляра, проведенного из точки М1 на прямую a. Второй случай говорит о том, что точки этой плоскости необходимо искать в качестве высоты параллелограмма.

Первый способ

Из определения имеем, что расстояние от точки М1_,расположенной на прямой а, является длиной перпендикуляра М1Н1_,тогда получим, что при найденных координатах точки Н1 , тогда найдем расстояние между M1(x1, y1, z1) и H1(x1, y1, z1), исходя из формулы M1H1=x2-x12+y2-y12+z2-z12.

Получаем, что все решение идет к тому, чтобы найти координаты основания перпендикуляра, проведенного из М1 на прямую a. Это производится следующим образом: Н1 является точкой, где пересекаются прямая a с плоскостью, которая проходит через заданную точку.

Значит, алгоритм определения расстояния от точки M1(x1, y1, z1) к прямой a пространства подразумевает несколько пунктов:

Определение 5

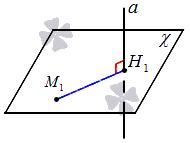
составление уравнение плоскости χ в качестве уравнения плоскости, проходящего через заданную точку, находящуюся перпендикулярно прямой;
определение координат (x2, y2, z2), принадлежавших точке Н1, которая является точкой пересечения прямой a и плоскости χ;
вычисление расстояния от точки до прямой при помощи формулы M1H1=x2-x12+y2-y12+z2-z12.

Второй способ

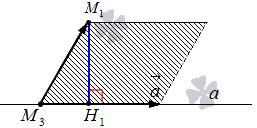
Из условия имеем прямую a, тогда можем определить направляющий вектор a→=ax, ay, az с координатами x3, y3, z3 и определенной точки М3_,принадлежащей прямой a. При наличии координат точек M1(x1, y1) и M3x3, y3, z3 можно произвести вычисление M3M1→:

M3M1→=(x1-x3, y1-y3, z1-z3)

Следует отложить векторы a→=ax, ay, az и M3M1→=x1-x3, y1-y3, z1-z3 из точки М3, соединим и получим фигуру параллелограмма. М1Н1 является высотой параллелограмма.

Рассмотрим на рисунке, приведенном ниже.

Имеем, что высота М1Н1 является искомым расстоянием, тогда необходимо найти его по формуле. То есть ищем M1H1.

Обозначим площадь параллелограмма за букву S, находится по формуле, используя вектор a→=(ax, ay, az) и M3M1→=x1-x3. y1-y3, z1-z3. Формула площади имеет вид S=a→×M3M1→. Также площадь фигуры равняется произведению длин его сторон на высоту, получим, что S=a→·M1H1 с a→=ax2+ay2+az2, являющимся длиной вектора a→=(ax, ay, az), являющейся равной стороне параллелограмма. Значит, M1H1 является расстоянием от точки до прямой. Ее нахождение производится по формуле M1H1=a→×M3M1→a→.

Для нахождения расстояния от точки с координатами M1(x1, y1, z1) до прямой a в пространстве, необходимо выполнить несколько пунктов алгоритма:

Определение 6

определение направляющего вектора прямой a – a→=(ax, ay, az);
вычисление длины направляющего вектора a→=ax2+ay2+az2;
получение координат x3, y3, z3, принадлежавших точке М₃, находящейся на прямой а;
вычисление координат вектора M3M1→;
нахождение векторного произведения векторов a→(ax, ay, az) и M3M1→=x1-x3, y1-y3, z1-z3 в качестве a→×M3M1→=i→j→k→axayazx1-x3y1-y3z1-z3 для получения длины по формуле a→×M3M1→;
вычисление расстояния от точки до прямой M1H1=a→×M3M1→a→.

Решение задач на нахождение расстояния от заданной точки до заданной прямой в пространстве

Пример 5

Найти расстояние от точки с координатами M12, -4, -1 к прямой x+12=y-1=z+55.

Решение

Первый способ начинается с записи уравнения плоскости χ, проходящей через М1и перпендикулярно заданной точке. Получаем выражение вида:

2·(x-2)-1·(y-(-4))+5·(z-(-1))=0⇔2x-y+5z-3=0

Нужно найти координаты точки H1, являющейся точкой пересечения с плоскостью χ к заданной по условию прямой. Следует переходить от канонического вида к пересекающемуся. Тогда получаем систему уравнений вида:

x+12=y-1=z+55⇔-1·(x+1)=2·y5·(x+1)=2·(z+5)5·y=-1·(z+5)⇔x+2y+1=05x-2z-5=05y+z+5=0⇔x+2y+1=05x-2z-5=0

Необходимо вычислить систему x+2y+1=05x-2z-5=02x-y+5z-3=0⇔x+2y=-15x-2z=52x-y+5z=3 по методу Крамера, тогда получаем, что:

∆=12050-22-15=-60∆x=-12050-23-15=-60⇔x=∆x∆=-60-60=1∆y=1-10552235=60⇒y=∆y∆=60-60=-1∆z=12-15052-13=0⇒z=∆z∆=0-60=0

Отсюда имеем, что H1(1, -1, 0).

Необходимо рассчитать расстояние между точками с координатами M1(2, -4, -1) и H1(1, -1, 0) по формуле:

M1H1=1-22+-1–42+0–12=11

Второй способ необходимо начать с поиска координат в каноническом уравнении. Для этого необходимо обратит внимание на знаменатели дроби. Тогда a→=2, -1, 5 является направляющим вектором прямой x+12=y-1=z+55. Необходимо вычислить длину по формуле a→=22+(-1)2+52=30.

Понятно, что прямая x+12=y-1=z+55 пересекает точку M3(-1, 0, -5), отсюда имеем, что вектор с началом координат M3(-1, 0, -5) и его концом в точке M12, -4, -1 является M3M1→=3, -4, 4. Находим векторное произведение a→=(2, -1, 5) и M3M1→=(3, -4, 4).

Мы получаем выражение вида a→×M3M1→=i→j→k→2-153-44=-4·i→+15·j→-8·k→+20·i→-8·j→=16·i→+7·j→-5·k→

получаем, что длина векторного произведения равняется a→×M3M1→=162+72+-52=330.

Имеются все данные для использования формулы вычисления расстояния от точки для прямлой, поэтому применим ее и получим:

M1H1=a→×M3M1→a→=33030=11

Ответ: 11.

Источник

Что такое расстояние от точки до прямой

Определение

Расстояние от точки до прямой – это длина перпендикуляра, опущенного из точки на прямую.

При этом перпендикуляр – это наименьшее из расстояний от этой точки до точек прямой.

Расстояние от точки до прямой на плоскости, методы нахождения

Найти расстояние от точки до прямой можно двумя способами. С помощью теоремы Пифагора или прямоугольной системы координат. Рассмотрим первый метод.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Теорема Пифагора гласит, что прямоугольная система координат OXY имеет точку М₁ (x₁, y₁). Из нее к плоскости проведена прямая а. Уравнение плоскости имеет вид:

cos ax + cos by – p = 0.

Это уравнение равно по модулю значению, которое получается в левой части уравнения прямой при x = x₁, а y = y₁. Это значит, что:

M₁H₁ = cos ax₁ + cos by₁ – p

Доказательство

Прямой а соответствует уравнение плоскости, которое имеет вид:

cos ax + cos by – p = 0.

Тогда n → = (сos a, cos b) – это нормальный вектор прямой а с расстоянием от начала координат до прямой а с р единицами. При этом радиус вектор точки М₁ – ОМ₁ → = (х₁, у₁).

М₁Н₁ – прямая от точки до прямой. Проекции М₂ и Н₂ точек М₁ и Н₁ проходят через точку О с направляющим вектором n → = (cos a, cos b). Числовая проекция вектора ОМ₁ → = (х₁, у₁) направлена к n → = (cos a, cos b) как npn → OM₁ →. В итоге получаем М₁Н₁ = npn → ОМ → 1 – р.

Далее приводим равенство к виду М₁Н₁ = cos x₁ + cos b₁ – p. Из этого выходит npn → OM → 1 = cos ax₁ + cos by₁. Cкалярное произведение векторов дает формулу n → OM → 1 = n → npn → OM₁ → = 1npn → OM₁ → = npn → OM1 →.

Эта формула – произведение в координатной форме вида n →, OM₁ → = cos ax₁ + cos by₁. Из этого npn → OM₁ → = cos ax₁ +cos by₁. Отсюда следует, что M₁H₁ = npn → OM₁ → – p = cos ax1 + cos by1 – p.

Что и следовало доказать.

Согласно теореме Пифагора, чтобы найти расстояние от точки до прямой, нужно совершить следующие шаги:

Вывести уравнение прямой cos ax + cos by – p = 0, если его нет в задании.
Вычислить cos ax + cos by – p, где значение принимает М₁Н₁.

Рассмотрим второй метод. Если у точки Н₁ есть координаты (х₂, у₂), тогда расстояние от точки до прямой можно найти по формуле:

(left|M1H1right|=sqrt{left(x2-x1right)^2+left(y2-y1right)^2})

Найдем координаты точки Н1.

Прямая линия в ОХУ равна уравнению прямой на плоскости. Необходимо составить уравнение прямой b, проходящей через точку М₁ перпендикулярно прямой а. Н₁ – это точка пересечения прямых a и b. Для начала нужно найти общее уравнение прямой а, которое имеет вид А₁х + В₁у + С₁ = 0. Либо можно воспользоваться уравнением с угловым коэффициентом у = k₁x + b₁.

Далее нужно вывести уравнение прямой b, которое имеет вид А₂х + В₂у + С₂ = 0. Либо можно использовать уравнение по аналогии с прямой а: у = k₂x + b₂. Чтобы определить координаты точки Р1, нужно решить систему линейных уравнений:

(left{begin{array}{lc}А1х;+;В1у;+;С1;=;0&\А2х;+;В2у;+;С2;=;0&end{array}right.) либо ( left{begin{array}{l}у;=;k1x;+;b1\у;=;k2x;+;b2end{array}right.)

Конечное расстояние получают с помощью формулы:

(left|M1H1right|=sqrt{left(x2-x1right)^2+left(y2-y1right)^2})

Формулы для нахождения расстояния

Длину перпендикуляра также можно найти с помощью следующей формулы:

(d;=;;frac{left|Atimes M_x+Btimes M_y+Cright|}{sqrt{A^2+B^2}})

Решение уравнений

Пример 1

Вычислить расстояние между прямой 3x + 4y – 6 = 0 и точкой M(-1, 3).

Решение

(d;=;;frac{left|3times(-1)+4times3-6right|}{sqrt{3^2+4^2}}=frac{left|-3+12-6right|}{sqrt{9+16}}=frac{left|3right|}{sqrt{25}}=frac{left|3right|}5=0,6)

Ответ: 0,6.

Пример 2

Найти расстояние между прямой 12x + 5y – 17 = 0 и точкой M(-3, 8).

Решение

(d;=;;frac{left|12times(-3)+5times8-17right|}{sqrt{12^2+5^2}}=frac{left|-36+40-17right|}{sqrt{144+25}}=frac{left|-13right|}{sqrt{169}}=frac{left|13right|}{13}=1)

Ответ: 1.

Пример 3

Вычислить расстояние между прямой 4x + 3y – 3 = 0 и точкой M(-2, 5).

Решение

(d;=;;frac{left|4times(-2)+3times5-3right|}{sqrt{4^2+3^2}}=frac{left|-8+15-3right|}{sqrt{16+9}}=frac{left|4right|}{sqrt{25}}=frac{left|4right|}5=0,8)

Ответ: 0,8.

Примеры задач для нахождения расстояния от точки до прямой

Задача 1

Дана треугольная пирамида АВСD. Ее грани ABС и ABD представляют собой равные равнобедренные треугольники с прямыми углами при вершине A.

Найти расстояние от точки A до грани ACD, если высота пирамиды равна h и равна CD.

Решение

Так как △BCD равнобедренный, то BC ⊥ CD, K – середина CD. Так же AK ⊥ CD. Получается, перпендикуляр BH на плоскость ACD упадет на прямую AK (удовлетворяет теореме о трех перпендикулярах: HK – проекция, BK – наклонная, обе перпендикулярны CD).

По теореме Пифагора (BK=frac{hsqrt3}2).

Тогда (tg ∠ AKB = frac{AB}{BK}=frac{2sqrt3}3=frac{BH}{HK}).

Значит, (BH = 2sqrt3x), (HK = 3x).

По теореме Пифагора из △ BHK находим (x = frac1{2sqrt7}h ⇒ BH = sqrt{frac37}h).

Ответ: (sqrt{frac37}h).

Задача 2

Дана правильная четырехугольная пирамида ABCDE с вершиной A. Через точку пересечения диагоналей основания провели плоскость α перпендикулярно ребру AB.

Найти расстояние от точки N до плоскости α, если N – середина (BE = 2sqrt2), а высота пирамиды равна 11.

Решение

По теореме о трех перпендикулярах AB ⊥ CE как наклонная (AO ⊥ (BCD), OB ⊥ CE – проекция). Получаем две пересекающиеся прямые OK и СЕ из плоскости α. Значит, сечением является треугольник СKЕ.

Проведем MN ∥ СЕ. Тогда MN ∥ α. Так как расстояние от любой точки прямой, параллельной плоскости, до этой плоскости одинаково, то:

ρ(N,α)=ρ(Q,α)

где ρ — расстояние.

Т.к. по условию SA⊥α, то проведем QH∥SA⇒QH⊥α. По построению MN – средняя линия △BAD, следовательно:

ВQ = QO ⇒ QH – средняя линия △ KВO ⇒ QH = frac12 ВK.

Рассмотрим △ АВO = 2. Из △ ВKO ∼ △ ВАO (⇒ frac{ВК}{ВО}=frac{ВО}{ВА} ⇒ ВK = frac{4sqrt5}{25} ⇒ QH = frac{2sqrt5}{25}).

Ответ: (frac{2sqrt5}{25}).

Задача 3

Дано: в цилиндре параллельно диаметру ВС = 10 в нижнем основании проведена прямая, пересекающая окружность нижнего основания в точках Р и Z, причем PZ = 6. Через отрезок PZ проведена плоскость α под углом 15 градусов к плоскости осевого сечения ВСDE.

Найти расстояние от центра нижнего основания до плоскости α.

Решение

Обозначим за OQ – ось цилиндра. Тогда OQ ⊥ BC ⇒ OQ ⊥ p (OQ ∩ p = L).

Проведем OR ⊥ PZ ⇒ по теореме о трех перпендикулярах RL ⊥ PZ ⇒ RL ⊥ p ⇒ ∠ RLO – угол между плоскостями BCDE и α.

Так как и OR⊥PZ и LR⊥PZ, то перпендикуляр из точки O на плоскость α упадет на прямую LR.

Рассмотрим △ OPR: OP = 5, PR = 3, ∠ ORP = 90° ⇒ OR = 4.

Рассмотрим △ LOR: (∠ HOR = ∠ RLO = 15° ⇒ OH = OR ⋅ cos⁡15° = 4 ⋅ cos⁡(45° − 30°) = sqrt6+sqrt2).

Ответ: (sqrt6+sqrt2).

Источник

Расстояние от точки до прямой на плоскости — это кратчайшее расстояние от точки до прямой в евклидовой геометрии. Расстояние равно длине отрезка, который соединяет точку с прямой и перпендикулярен прямой. Формула вычисления расстояния может быть получена и выражена несколькими способами.

Знание наименьшего расстояния от точки до прямой может быть полезно во многих случаях, например, для поиска кратчайшего пути для выхода на дорогу, определение разброса графа, и подобное. В регрессии Деминга, процедуре линейного сглаживания, если зависимые и независимые переменные имеют одну и ту же дисперсию, регрессия сводится к ортогональной регрессии, в которой степень приближения измеряется для каждой точки как расстояние от точки до регрессионной прямой.

Декартова система координат[править | править код]

Прямая задана уравнением[править | править код]

Когда прямая на плоскости задана уравнением ax + by + c = 0, где a, b и c — такие вещественные константы, что a и b не равны нулю одновременно, и расстояние от прямой до точки (x₀,y₀) равно ^[1]

${displaystyle operatorname {distance} (ax+by+c=0,(x_{0},y_{0}))={frac {|ax_{0}+by_{0}+c|}{sqrt {a^{2}+b^{2}}}}.}$

Точка на прямой, наиболее близкая к (x₀,y₀), имеет координаты ^[2]

${displaystyle x={frac {b(bx_{0}-ay_{0})-ac}{a^{2}+b^{2}}}}$

и ${displaystyle y={frac {a(-bx_{0}+ay_{0})-bc}{a^{2}+b^{2}}}.}$

Горизонтальные и вертикальные прямые

В общем уравнении прямой ax + by + c = 0 коэффициенты a и b не могут быть одновременно равны нулю пока c ненулевое, а в случае всех нулевых коэффициентов уравнение не задаёт прямую. Если a = 0, а b ≠ 0, прямая горизонтальна и имеет уравнение y = –c/b. Расстояние от (x₀, y₀) до этой прямой определяется вертикальным отрезком длины |y₀ — (-c/b)| = |by₀ + c| / |b| (согласно формуле). Аналогичным образом, для вертикальных прямых (b = 0) расстояние между той же точкой и прямой равно |ax₀ + c| / |a| и измеряется вдоль горизонтального отрезка.

Нормированное уравнение прямой

Нормированное уравнение прямой — это уравнение вида

{displaystyle xcos alpha +ysin alpha -p=0}

Нормированное уравнение получается из общего уравнения прямой ax + by + c = 0 делением всех членов на ${displaystyle {sqrt {a^{2}+b^{2}}}}$ .
Тогда расстояние от точки (x₀, y₀) до прямой равно абсолютному значению отклонения и вычисляется по формуле ^[3]^[4]

${displaystyle |d|=|x_{0}cos alpha +y_{0}sin alpha -p|}$

Прямая задана двумя точками[править | править код]

Если прямая проходит через две точки P₁=(x₁,y₁) и P₂=(x₂,y₂), и необходимо найти расстояние от ${displaystyle M=(x_{0},y_{0})}$ до прямой, то можно воспользоваться следующими способами:

Способ 1. Искомое расстояние равно

${displaystyle operatorname {distance} (P_{1},P_{2},(x_{0},y_{0}))={frac {|(y_{2}-y_{1})x_{0}-(x_{2}-x_{1})y_{0}+x_{2}y_{1}-y_{2}x_{1}|}{sqrt {(y_{2}-y_{1})^{2}+(x_{2}-x_{1})^{2}}}}.}$

Знаменатель этого выражения равен расстоянию между точками P₁ и P₂. Числитель равен удвоенной площади треугольника с вершинами (x₀,y₀), P₁ и P₂ (см. Общая формула площади треугольника в декартовых координатах). Выражение эквивалентно ${textstyle h={frac {2A}{b}}}$ , что может быть получено преобразованием стандартной формулы площади треугольника: ${textstyle A={frac {1}{2}}bh}$ , где b — длина стороны, а h — высота на эту сторону из противолежащей вершины.

Способ 2. Сначала находится ближайшая точка на прямой к точке по формуле

${displaystyle M_{p}=P_{1}+{overrightarrow {P_{1}P_{2}}}*{({overrightarrow {P_{1}P_{2}}},{overrightarrow {P_{1}M}}) over lVert {overrightarrow {P_{1}P_{2}}}rVert ^{2}}}$ .

Тогда искомое расстояние равно

${displaystyle operatorname {distance} (P_{1},P_{2},M)=lVert {overrightarrow {MM_{p}}}rVert }$ .

Доказательства[править | править код]

Алгебраическое доказательство[править | править код]

Это доказательство верно, только когда прямая не является ни вертикальной, ни горизонтальной. То есть мы предполагаем, что ни a, ни b в уравнении не равны нулю.

Прямая с уравнением ax + by + c = 0 имеет наклон –a/b, так что любая прямая, перпендикулярная к заданной, имеет наклон b/a. Пусть (m, n) — точка пересечения прямой ax + by + c = 0 и перпендикулярной прямой, проходящей через точку (x₀, y₀). Прямая, проходящая через эти две точки, перпендикулярна исходной прямой, так что

${displaystyle {frac {y_{0}-n}{x_{0}-m}}={frac {b}{a}}.}$

Таким образом,
${displaystyle a(y_{0}-n)-b(x_{0}-m)=0,}$
и после возведения в квадрат получим:

${displaystyle a^{2}(y_{0}-n)^{2}+b^{2}(x_{0}-m)^{2}-2ab(y_{0}-n)(x_{0}-m)=0.}$

Рассмотрим,

${displaystyle (a(x_{0}-m)+b(y_{0}-n))^{2}=a^{2}(x_{0}-m)^{2}+2ab(y_{0}-n)(x_{0}-m)+b^{2}(y_{0}-n)^{2}=(a^{2}+b^{2})((x_{0}-m)^{2}+(y_{0}-n)^{2})}$

Здесь использовано возведённое в квадрат выражение. Но

${displaystyle (a(x_{0}-m)+b(y_{0}-n))^{2}=(ax_{0}+by_{0}-am-bn)^{2}=(ax_{0}+by_{0}+c)^{2}}$

так как точка (m, n) расположена на прямой ax + by + c = 0.
Таким образом,

${displaystyle (a^{2}+b^{2})((x_{0}-m)^{2}+(y_{0}-n)^{2})=(ax_{0}+by_{0}+c)^{2}}$

Из этого получаем длину отрезка между этими двумя точками:

${displaystyle d={sqrt {(x_{0}-m)^{2}+(y_{0}-n)^{2}}}={frac {|ax_{0}+by_{0}+c|}{sqrt {a^{2}+b^{2}}}}.}$

^[5].

Геометрическое доказательство[править | править код]

Это доказательство верно, только когда прямая не является ни вертикальной, ни горизонтальной. Баллантин и Джерберт^[6] не упомянули это ограничение в своей статье.

Опустим перпендикуляр из точки P с координатами (x₀, y₀) на прямую с уравнением Ax + By + C = 0. Обозначим основание перпендикуляра буквой R. Проведём вертикальную прямую через P и обозначим пересечение этой вертикальной прямой с исходной прямой буквой S. В произвольной точке T на прямой нарисуем прямоугольный треугольник TVU, катеты которого являются горизонтальными и вертикальными отрезками, а длина горизонтального отрезка равна |B| (см. рисунок). Вертикальный катет треугольника ∆TVU будет иметь длину |A|, поскольку наклон прямой равен –A/B.

Треугольники ∆SRP и ∆UVT подобны, так как они оба прямоугольные и ∠PSR ≅ ∠VUT, поскольку являются соответственными углами двух параллельных прямых PS и UV (вертикальные прямые) и секущей (исходная прямая)^[7]. Выпишем отношения сторон этих треугольников:

${displaystyle {frac {|{overline {PR}}|}{|{overline {PS}}|}}={frac {|{overline {TV}}|}{|{overline {TU}}|}}.}$

Если точка S имеет координаты (x₀,m), то |PS| = |y₀ — m| и расстояние от P до прямой равно:

${displaystyle |{overline {PR}}|={frac {|y_{0}-m||B|}{sqrt {A^{2}+B^{2}}}}.}$

Поскольку S находится на прямой, мы можем найти значение m,

${displaystyle m={frac {-Ax_{0}-C}{B}},}$

и получаем: ^[6]

${displaystyle |{overline {PR}}|={frac {|Ax_{0}+By_{0}+C|}{sqrt {A^{2}+B^{2}}}}.}$

Другой вариант этого доказательства — поместить точку V в точку P и вычислить площадь треугольника ∆UVT двумя способами, после чего получим ,
где D — высота треугольника ∆UVT на гипотенузу из точки P. Формула расстояния может быть использована, чтобы выразить , и в терминах координат P и коэффициентов уравнения исходной прямой, в результате чего получим требуемую формулу.

Доказательство с помощью проекции вектора[править | править код]

Пусть P — точка с координатами (x₀, y₀) и пусть исходная прямая имеет уравнение ax + by + c = 0. Пусть Q = (x₁, y₁) — любая точка на прямой и n — вектор (a, b) с началом в точке Q. Вектор n перпендикулярен прямой, и расстояние d от точки P до прямой равно длине ортогональной проекции на n. Длина этой проекции равна:

${displaystyle d={frac {|{overrightarrow {QP}}cdot mathbf {n} |}{|mathbf {n} |}}.}$

Теперь

${displaystyle {overrightarrow {QP}}=(x_{0}-x_{1},y_{0}-y_{1}),}$

так что ${displaystyle {overrightarrow {QP}}cdot mathbf {n} =a(x_{0}-x_{1})+b(y_{0}-y_{1})}$

и ${displaystyle |mathbf {n} |={sqrt {a^{2}+b^{2}}}.}$

Тогда

${displaystyle d={frac {|a(x_{0}-x_{1})+b(y_{0}-y_{1})|}{sqrt {a^{2}+b^{2}}}}.}$

Поскольку Q лежит на прямой, ${displaystyle c=-ax_{1}-by_{1}}$ , а тогда ^[8]^[9]^[10]

${displaystyle d={frac {|ax_{0}+by_{0}+c|}{sqrt {a^{2}+b^{2}}}}.}$

Другие формулы[править | править код]

Можно получить другие выражения для кратчайшего расстояния от точки до прямой. Эти выводы тоже требуют, чтобы прямая не была вертикальной или горизонтальной.

Пусть точка P задана координатами ( ${displaystyle x_{0},y_{0}}$ ).
Пусть прямая задана уравнением y=mx+k . Уравнение прямой, перпендикулярной исходной прямой и проходящей через точку P, задаётся уравнением ${displaystyle y={frac {x_{0}-x}{m}}+y_{0}}$ .

Точка, в которой эти две прямые пересекаются, является ближайшей точкой на исходной прямой для точки P. Тогда:

${displaystyle mx+k={frac {x_{0}-x}{m}}+y_{0}.}$

Мы можем решить это уравнение по x,

${displaystyle x={frac {x_{0}+my_{0}-mk}{m^{2}+1}}.}$

Координату y точки пересечения можно найти, подставив значение x в уравнение исходной прямой,

${displaystyle y=m{frac {(x_{0}+my_{0}-mk)}{m^{2}+1}}+k.}$

Подставив полученные значения в формулу расстояния ${displaystyle d={sqrt {(X_{2}-X_{1})^{2}+(Y_{2}-Y_{1})^{2}}}}$ , получим формулу кратчайшего расстояния от точки до прямой:

${displaystyle d={sqrt {left({{frac {x_{0}+my_{0}-mk}{m^{2}+1}}-x_{0}}right)^{2}+left({m{frac {x_{0}+my_{0}-mk}{m^{2}+1}}+k-y_{0}}right)^{2}}}.}$

Если заметить, что m = –a/b и k = –c/b для уравнения ax + by + c = 0, после небольших выкладок получим стандартное выражение^[2].

Формулировка с помощью векторов[править | править код]

Иллюстрация формулировки с помощью векторов.

Запишем прямую в векторном виде:

{displaystyle mathbf {x} =mathbf {a} +tmathbf {n} }

где x — вектор, задающий координаты любой точки на прямой, n — единичный вектор в направлении прямой, a — вектор, задающий две координаты точки на прямой, а t — скаляр. То есть для получения точки x на прямой начинаем с точки a на прямой и двигаемся на расстояние t вдоль прямой.

Расстояние от произвольной точки p до прямой задаётся формулой

{displaystyle operatorname {distance} (mathbf {x} =mathbf {a} +tmathbf {n} ,mathbf {p} )=|(mathbf {a} -mathbf {p} )-((mathbf {a} -mathbf {p} )cdot mathbf {n} )mathbf {n} |.}

Эта формула геометрически строится следующим образом: — это вектор из p в точку a на прямой. Тогда — это длина проекции на прямую, а тогда

{displaystyle ((mathbf {a} -mathbf {p} )cdot mathbf {n} )mathbf {n} }

— это вектор, являющийся проекцией на прямую. Тогда

{displaystyle (mathbf {a} -mathbf {p} )-((mathbf {a} -mathbf {p} )cdot mathbf {n} )mathbf {n} }

является компонентой вектора , перпендикулярной прямой. Следовательно, расстояние от точки до прямой равно норме этого вектора^[11]. Эта формула может быть использована и в более высоких размерностях.

Другая формулировка с помощью векторов[править | править код]

Если векторное пространство ортонормально, а прямая (d ) проходит через точку B и имеет вектор направления^[en] vec u , то расстояние от точки A до прямой (d) равно

${displaystyle d(mathrm {A} ,(d))={frac {left|{overrightarrow {mathrm {BA} }}wedge {vec {u}}right|}{|{vec {u}}|}}}$

где — векторное произведение векторов и vec u , а — норма вектора vec u .

Обобщения[править | править код]

Расстояние от точки в трёхмерном пространстве до плоскости задаётся аналогичной формулой^[12]:

${displaystyle operatorname {distance} (ax+by+cz+d=0,(x_{0},y_{0},z_{0}))={frac {|ax_{0}+by_{0}+cz_{0}+d|}{sqrt {a^{2}+b^{2}+c^{2}}}}.}$

См. также[править | править код]

Пересечение двух прямых^[en]
Расстояние между двумя прямыми
Расстояние между скрещивающимися прямыми

Примечания[править | править код]

↑ Larson, Hostetler, 2007, p. 452.
↑ ¹ ² Larson, Hostetler, 2007, p. 522.
↑ Привалов, 1966, с. 67.
↑ Делоне, Райков, 1948, с. 195.
↑ Laudanski, 2014.
↑ ¹ ² Ballantine, Jerbert, 1952, с. 242–243.
↑ Если два треугольника окажутся по разные стороны от исходной прямой, эти углы будут накрест лежащими, а потому опять равными.
↑ Anton, 1994, с. 138-9.
↑ Федотов, Карпов, 2005, с. 86.
↑ Моденов, 1967, с. 152.
↑ Sunday, Dan. Lines and Distance of a Point to a Line. // softSurfer. Дата обращения: 6 декабря 2013. Архивировано 14 декабря 2017 года.
↑ OnlineMSchool. Дата обращения: 2 декабря 2020. Архивировано 17 января 2021 года.

Литература[править | править код]

Делоне Б. Н., Райков Д. А. . Аналитическая геометрия. T. 1. — М., Л.: ОГИЗ, 1948. — 456 с.
Моденов П. С. . Аналитическая геометрия. — М.: Изд-во Моск. ун-та, 1967. — 697 с.
Привалов И. И. . Аналитическая геометрия. 13-е изд. — М.: Наука, 1966. — 272 с.
Федотов А. Г., Карпов Б. В. . Аналитическая геометрия. — М.: МГИЭМ, 2005. — 158 с. — ISBN 5-94506-116-6.
Anton H. . Elementary Linear Algebra. 7th ed. — Somerset: John Wiley & Sons, 1994. — ISBN 0-471-58742-7.
Ballantine J. P., Jerbert A. R. Distance from a Line or Plane to a Point // American Mathematical Monthly. — 1952. — Vol. 59. — P. 242—243. — doi:10.2307/2306514.
Larson R., Hostetler R. . Precalculus: A Concise Course. — Boston: Houghton Mifflin, 2007. — xvii + 526 + 102 p. — ISBN 0-618-62719-7.
Laudański L. M. . Between Certainty and Uncertainty: Statistics and Probability in Five Units with Notes on Historical Origins and Illustrative Numerical Examples. — Berlin; Heidelberg: Springer Verlag, 2014. — x + 318 p. — (Intelligent Systems Reference Library, vol. 31). — ISBN 978-3-642-25696-7.

Дополнительная литература[править | править код]

Deza M. M., Deza E. . Encyclopedia of Distances. 2nd ed. — Berlin; Heidelberg: Springer Verlag, 2013. — xviii + 650 p. — ISBN 978-3-642-30957-1. — P. 86.

Источник

From Wikipedia, the free encyclopedia

In Euclidean geometry, the distance from a point to a line is the shortest distance from a given point to any point on an infinite straight line. It is the perpendicular distance of the point to the line, the length of the line segment which joins the point to nearest point on the line. The formula for calculating it can be derived and expressed in several ways.

Knowing the distance from a point to a line can be useful in various situations—for example, finding the shortest distance to reach a road, quantifying the scatter on a graph, etc. In Deming regression, a type of linear curve fitting, if the dependent and independent variables have equal variance this results in orthogonal regression in which the degree of imperfection of the fit is measured for each data point as the perpendicular distance of the point from the regression line.

Line defined by an equation[edit]

In the case of a line in the plane given by the equation ax + by + c = 0, where a, b and c are real constants with a and b not both zero, the distance from the line to a point (x₀, y₀) is^[1]^[2]^: p.14

$operatorname{distance}(ax+by+c=0, (x_0, y_0)) = frac{|ax_0+by_0+c|}{sqrt{a^2+b^2}}.$

The point on this line which is closest to (x₀, y₀) has coordinates:^[3]

$x={frac {b(bx_{0}-ay_{0})-ac}{a^{2}+b^{2}}}{text{ and }}y={frac {a(-bx_{0}+ay_{0})-bc}{a^{2}+b^{2}}}.$

Horizontal and vertical lines

In the general equation of a line, ax + by + c = 0, a and b cannot both be zero unless c is also zero, in which case the equation does not define a line. If a = 0 and b ≠ 0, the line is horizontal and has equation y = −c/b. The distance from (x₀, y₀) to this line is measured along a vertical line segment of length |y₀ − (−c/b)| = |by₀ + c|/|b| in accordance with the formula. Similarly, for vertical lines (b = 0) the distance between the same point and the line is |ax₀ + c|/|a|, as measured along a horizontal line segment.

Line defined by two points[edit]

If the line passes through two points P₁ = (x₁, y₁) and P₂ = (x₂, y₂) then the distance of (x₀, y₀) from the line is:^[4]

${displaystyle operatorname {distance} (P_{1},P_{2},(x_{0},y_{0}))={frac {|(x_{2}-x_{1})(y_{1}-y_{0})-(x_{1}-x_{0})(y_{2}-y_{1})|}{sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}}.}$

The denominator of this expression is the distance between P₁ and P₂. The numerator is twice the area of the triangle with its vertices at the three points, (x₀, y₀), P₁ and P₂. See: Area of a triangle § Using coordinates. The expression is equivalent to h = 2A/b, which can be obtained by rearranging the standard formula for the area of a triangle: A = 1/2 bh, where b is the length of a side, and h is the perpendicular height from the opposite vertex.

Line defined by point and angle[edit]

If the line passes through the point P = (P_x, P_y) with angle θ, then the distance of some point (x₀, y₀) to the line is

${displaystyle operatorname {distance} (P,theta ,(x_{0},y_{0}))=|cos(theta )(P_{y}-y_{0})-sin(theta )(P_{x}-x_{0})|}$

Proofs[edit]

An algebraic proof[edit]

This proof is valid only if the line is neither vertical nor horizontal, that is, we assume that neither a nor b in the equation of the line is zero.

The line with equation ax + by + c = 0 has slope −a/b, so any line perpendicular to it will have slope b/a (the negative reciprocal). Let (m, n) be the point of intersection of the line ax + by + c = 0 and the line perpendicular to it which passes through the point (x₀, y₀). The line through these two points is perpendicular to the original line, so

$frac{y_0 - n}{x_0 - m}=frac{b}{a}.$

Thus,

and by squaring this equation we obtain:

a^2(y_0 - n)^2 + b^2(x_0 - m)^2 = 2ab(y_0 - n)(x_0 - m).

Now consider,

${displaystyle {begin{aligned}(a(x_{0}-m)+b(y_{0}-n))^{2}&=a^{2}(x_{0}-m)^{2}+2ab(y_{0}-n)(x_{0}-m)+b^{2}(y_{0}-n)^{2}\&=left(a^{2}+b^{2}right)left((x_{0}-m)^{2}+(y_{0}-n)^{2}right)end{aligned}}}$

using the above squared equation. But we also have,

${displaystyle (a(x_{0}-m)+b(y_{0}-n))^{2}=(ax_{0}+by_{0}-am-bn)^{2}=(ax_{0}+by_{0}+c)^{2}}$

since (m, n) is on ax + by + c = 0.
Thus,

${displaystyle left(a^{2}+b^{2}right)left((x_{0}-m)^{2}+(y_{0}-n)^{2}right)=(ax_{0}+by_{0}+c)^{2}}$

and we obtain the length of the line segment determined by these two points,

${displaystyle d={sqrt {(x_{0}-m)^{2}+(y_{0}-n)^{2}}}={frac {|ax_{0}+by_{0}+c|}{sqrt {a^{2}+b^{2}}}}.}$

^[5]

A geometric proof[edit]

Diagram for geometric proof

This proof is valid only if the line is not horizontal or vertical.^[6]

Drop a perpendicular from the point P with coordinates (x₀, y₀) to the line with equation Ax + By + C = 0. Label the foot of the perpendicular R. Draw the vertical line through P and label its intersection with the given line S. At any point T on the line, draw a right triangle TVU whose sides are horizontal and vertical line segments with hypotenuse TU on the given line and horizontal side of length |B| (see diagram). The vertical side of ∆TVU will have length |A| since the line has slope –A/B.

∆PRS and ∆TVU are similar triangles, since they are both right triangles and ∠PSR ≅ ∠TUV since they are corresponding angles of a transversal to the parallel lines PS and UV (both are vertical lines).^[7] Corresponding sides of these triangles are in the same ratio, so:

$frac{|overline{PR}|}{|overline{PS}|} = frac{|overline{TV}|}{|overline{TU}|}.$

If point S has coordinates (x₀,m) then |PS| = |y₀ – m| and the distance from P to the line is:

$|overline{PR} | = frac{|y_0 - m||B|}{sqrt{A^2 + B^2}}.$

Since S is on the line, we can find the value of m,

$m = frac{-Ax_0 - C}{B},$

and finally obtain:^[8]

$|overline{PR}| = frac{|Ax_0 + By_0 + C|}{sqrt{A^2 + B^2}}.$

A variation of this proof is to place V at P and compute the area of the triangle ∆UVT two ways to obtain that
where D is the altitude of ∆UVT drawn to the hypotenuse of ∆UVT from P. The distance formula can then used to express , , and in terms of the coordinates of P and the coefficients of the equation of the line to get the indicated formula.^{[citation needed]}

A vector projection proof[edit]

Let P be the point with coordinates (x₀, y₀) and let the given line have equation ax + by + c = 0. Also, let Q = (x₁, y₁) be any point on this line and n the vector (a, b) starting at point Q. The vector n is perpendicular to the line, and the distance d from point P to the line is equal to the length of the orthogonal projection of on n. The length of this projection is given by:

$d = frac{|overrightarrow{QP} cdot mathbf{n}|}{| mathbf{n}|}.$

Now,

$overrightarrow{QP} = (x_0 - x_1, y_0 - y_1),$

so $overrightarrow{QP} cdot mathbf{n} = a(x_0 - x_1) + b(y_0 - y_1)$

and $| mathbf{n} | = sqrt{a^2 + b^2},$

thus

$d = frac{|a(x_0 - x_1) + b(y_0 - y_1)|}{sqrt{a^2 + b^2}}.$

Since Q is a point on the line, , and so,^[9]

$d = frac{|ax_0 + by_0 + c|}{sqrt{a^2 + b^2}}.$

Although the distance is given as a modulus, the sign can be useful to determine which side of the line the point is on, in a sense determined by the direction of normal vector (a,b)

Another formula[edit]

It is possible to produce another expression to find the shortest distance of a point to a line. This derivation also requires that the line is not vertical or horizontal.

The point P is given with coordinates ( $x_{0},y_{0}$ ).
The equation of a line is given by y=mx+k . The equation of the normal of that line which passes through the point P is given $y=frac{x_0-x}{m}+y_0$ .

The point at which these two lines intersect is the closest point on the original line to the point P. Hence:

$mx+k=frac{x_0-x}{m}+y_0.$

We can solve this equation for x,

$x=frac{x_0+my_0-mk}{m^2+1}.$

The y coordinate of the point of intersection can be found by substituting this value of x into the equation of the original line,

$y=mfrac{(x_0+my_0-mk)}{m^2+1}+k.$

Using the equation for finding the distance between 2 points, $d=sqrt{(X_2-X_1)^2+(Y_2-Y_1)^2}$ , we can deduce that the formula to find the shortest distance between a line and a point is the following:

${displaystyle d={sqrt {left({{frac {x_{0}+my_{0}-mk}{m^{2}+1}}-x_{0}}right)^{2}+left({m{frac {x_{0}+my_{0}-mk}{m^{2}+1}}+k-y_{0}}right)^{2}}}={frac {|k+mx_{0}-y_{0}|}{sqrt {1+m^{2}}}}.}$

Recalling that m = –a/b and k = – c/b for the line with equation ax + by + c = 0, a little algebraic simplification reduces this to the standard expression.^[3]

Vector formulation[edit]

Illustration of the vector formulation.

The equation of a line can be given in vector form:

Here a is a point on the line, and n is a unit vector in the direction of the line. Then as scalar t varies, x gives the locus of the line.

The distance of an arbitrary point p to this line is given by

{displaystyle operatorname {distance} (mathbf {x} =mathbf {a} +tmathbf {n} ,mathbf {p} )=|(mathbf {p} -mathbf {a} )-((mathbf {p} -mathbf {a} )cdot mathbf {n} )mathbf {n} |.}

This formula can be derived as follows: is a vector from a to the point p. Then is the projected length onto the line and so

{displaystyle mathbf {a} +((mathbf {p} -mathbf {a} )cdot mathbf {n} )mathbf {n} }

is a vector that is the projection of onto the line and represents the point on the line closest to . Thus

{displaystyle (mathbf {p} -mathbf {a} )-((mathbf {p} -mathbf {a} )cdot mathbf {n} )mathbf {n} }

is the component of perpendicular to the line. The distance from the point to the line is then just the norm of that vector.^[4] This more general formula is not restricted to two dimensions.

Another vector formulation[edit]

If the vector space is orthonormal and if the line goes through point a and has a direction vector n, the distance between point p and the line is^[10]

${displaystyle operatorname {distance} (mathbf {x} =mathbf {a} +tmathbf {n} ,mathbf {p} )={frac {left|(mathbf {p} -mathbf {a} )times mathbf {n} right|}{|mathbf {n} |}}.}$

Note that cross products only exist in dimensions 3 and 7.

Notes[edit]

^ Larson & Hostetler 2007, p. 452
^ Spain 2007
^ ^a ^b Larson & Hostetler 2007, p. 522
^ ^a ^b Sunday, Dan. “Lines and Distance of a Point to a Line”. softSurfer. Archived from the original on 2021-05-07.
^ Between Certainty and Uncertainty: Statistics and Probability in Five Units With Notes on Historical Origins and Illustrative Numerical Examples
^ Ballantine & Jerbert 1952 do not mention this restriction in their article
^ If the two triangles are on opposite sides of the line, these angles are congruent because they are alternate interior angles.
^ Ballantine & Jerbert 1952
^ Anton 1994, pp. 138-9
^ Weisstein, Eric W. “Point-Line Distance–3-Dimensional”. mathworld.wolfram.com. Retrieved 2021-06-06.

References[edit]

Anton, Howard (1994), Elementary Linear Algebra (7th ed.), John Wiley & Sons, ISBN 0-471-58742-7
Ballantine, J.P.; Jerbert, A.R. (1952), “Distance from a line or plane to a point”, American Mathematical Monthly, 59 (4): 242–243, doi:10.2307/2306514, JSTOR 2306514
Larson, Ron; Hostetler, Robert (2007), Precalculus: A Concise Course, Houghton Mifflin Co., ISBN 978-0-618-62719-6
Spain, Barry (2007) [1957], Analytical Conics, Dover Publications, ISBN 978-0-486-45773-4
Weisstein, Eric W. “Point-Line Distance–3-Dimensional”. MathWorld.

Расстояние от точки до прямой – определение

Расстояние от точки до прямой на плоскости – теория, примеры, решения

Решение задач на нахождение расстояния от заданной точки до заданной прямой на плоскости

Расстояние от точки до прямой в пространстве – теория, примеры, решения

Решение задач на нахождение расстояния от заданной точки до заданной прямой в пространстве

Что такое расстояние от точки до прямой

Расстояние от точки до прямой на плоскости, методы нахождения

Формулы для нахождения расстояния

Решение уравнений

Примеры задач для нахождения расстояния от точки до прямой

Декартова система координат[править | править код]

Прямая задана уравнением[править | править код]

Прямая задана двумя точками[править | править код]

Доказательства[править | править код]

Алгебраическое доказательство[править | править код]

Геометрическое доказательство[править | править код]

Доказательство с помощью проекции вектора[править | править код]

Другие формулы[править | править код]

Формулировка с помощью векторов[править | править код]

Другая формулировка с помощью векторов[править | править код]

Обобщения[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Дополнительная литература[править | править код]

Line defined by an equation[edit]

Line defined by two points[edit]

Line defined by point and angle[edit]

Proofs[edit]

An algebraic proof[edit]

A geometric proof[edit]

A vector projection proof[edit]

Another formula[edit]

Vector formulation[edit]

Another vector formulation[edit]

See also[edit]

Notes[edit]

References[edit]

Further reading[edit]

Вам также может понравиться

Найти как называется комнатный цветок

Как найти в консоли сервера

Как составить опись имущества при разводе образец в суд

Добавить комментарий Отменить ответ