Задание 14. Математика ЕГЭ. Радиус основания конуса равен 12, а высота конуса равна 5. Найдите расстояние от плоскости сечения до центра основания конуса.
Задание.
Радиус основания конуса равен 12, а высота конуса равна 5.
а) Постройте сечение конуса плоскостью, проходящей через вершину конуса и взаимно перпендикулярные образующие.
б) Найдите расстояние от плоскости сечения до центра основания конуса.
Решение:
а) Постройте сечение конуса плоскостью, проходящей через вершину конуса и взаимно перпендикулярные образующие.
Так как сечение проходит через взаимно перпендикулярные образующие, то искомое сечение есть прямоугольный треугольник ∆АВС. Угол ∠АСВ = 90°, АС и ВС – катеты, АВ – гипотенуза.
б) Найдите расстояние от плоскости сечения до центра основания конуса.
Расстоянием от точки до плоскости называется перпендикуляр, проведенный от точки до данной плоскости.
Треугольник ∆АВС – равнобедренный, так как АС = ВС (образующие конуса). Тогда СМ – медиана и высота треугольника ∆АВС. Треугольник ∆АОВ – равнобедренный, так как АО = ОВ = Rосн. Тогда ОМ – медиана и высота треугольника ∆АОВ.
Прямая СО перпендикулярна плоскости основания, СМ – наклонная к плоскости основания, МО – проекция наклонной МО на плоскость основания. Точка М – основание наклонной, через точку М проходит прямая АВ перпендикулярно проекции МО, тогда по теореме о трех перпендикулярах прямая АВ перпендикулярна наклонной СМ.
Прямая АВ перпендикулярна двум пересекающимся прямым СМ и МО, лежащим в плоскости СМО, следовательно, АВ перпендикулярна плоскости СМО. АВ лежит в плоскости АВС, значит, плоскости СМО и АВС перпендикулярны. Следовательно, расстоянием от центра О основания окружности до плоскости сечения АВС будет являться перпендикуляр ОК (высота треугольника ∆МОС).
Из прямоугольного треугольника ∆АСО найдем АС:
АС2 = АО2 + ОС2
АС2 = 122 + 52 = 169
АС = 13
Из прямоугольного треугольника ∆АВС найдем АВ:
АВ2 = АС2 + ВС2
АВ2 = 132 + 132 = 338
АВ = 13√2
МВ = 1/2·АВ
МВ = (13√2)/2
Из прямоугольного треугольника ∆МВО найдем ОМ:
ОМ2 = ОВ2 – МВ2
Из прямоугольного треугольника ∆МВС найдем МС:
МС2 = ВС2 – ВМ2
Рассмотрим прямоугольный треугольник ∆МОС, площадь этого треугольника можно найти по формуле:
или по формуле:
Ответ:
Оставить комментарий
Рубрики
- Демоверсия ЕГЭ по информатике
- Демоверсия ЕГЭ по математике
- Демоверсия ОГЭ по информатике
- Демоверсия ОГЭ по математике
- Материалы по аттестации
- Решаем ЕГЭ по математике
- Задание 1
- Задание 10
- Задание 11
- Задание 12
- Задание 13
- Задание 14
- Задание 15
- Задание 16
- Задание 2
- Задание 3
- Задание 4
- Задание 5
- Задание 6
- Задание 7
- Задание 8
- Задание 9
- Решаем ОГЭ по математике
- Задание 21
- Задание 22
- Задание 24
- Скачать экзаменационные варианты по информатике
- ЕГЭ по информатике
- ОГЭ по информатике
- Скачать экзаменационные варианты по математике
- ЕГЭ по математике
- ОГЭ по математике
- Тематическое планирование
Интересная комплексная задача по начертательной геометрии
Условие задачи
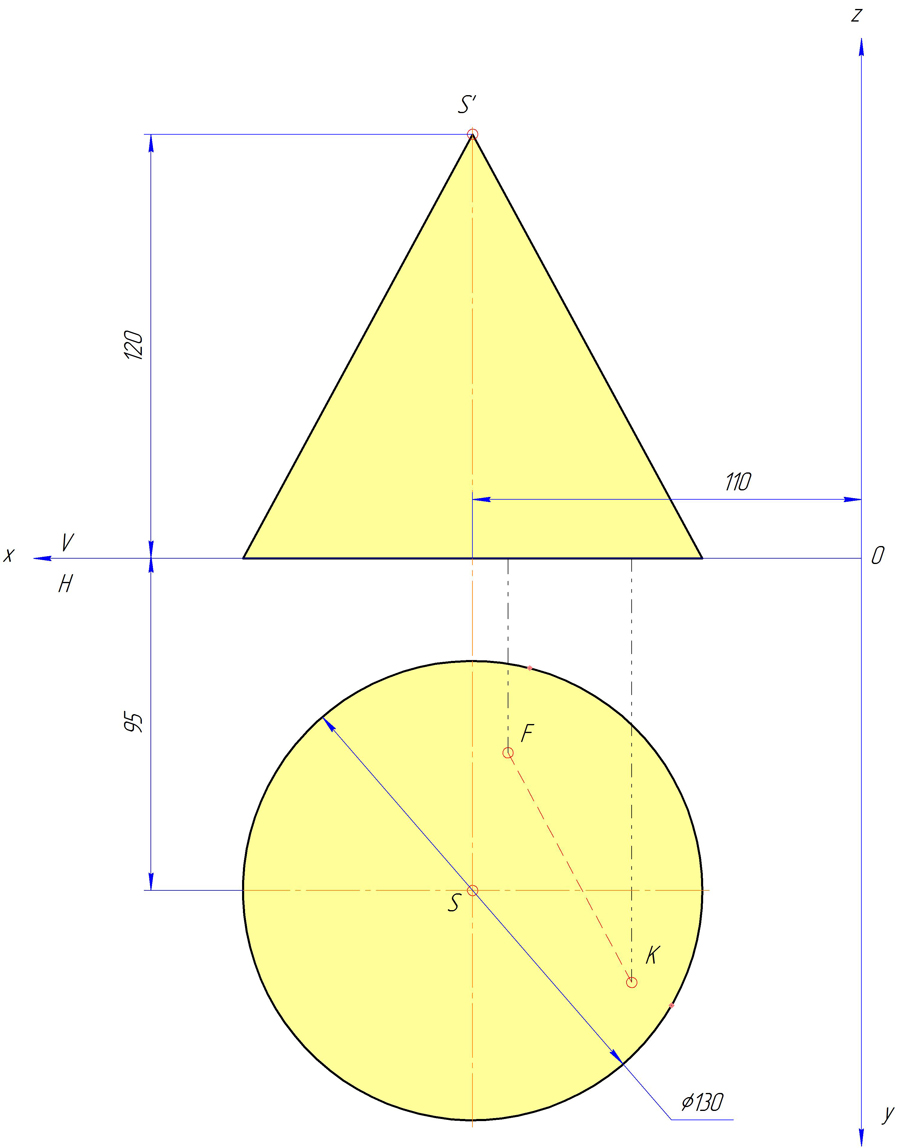
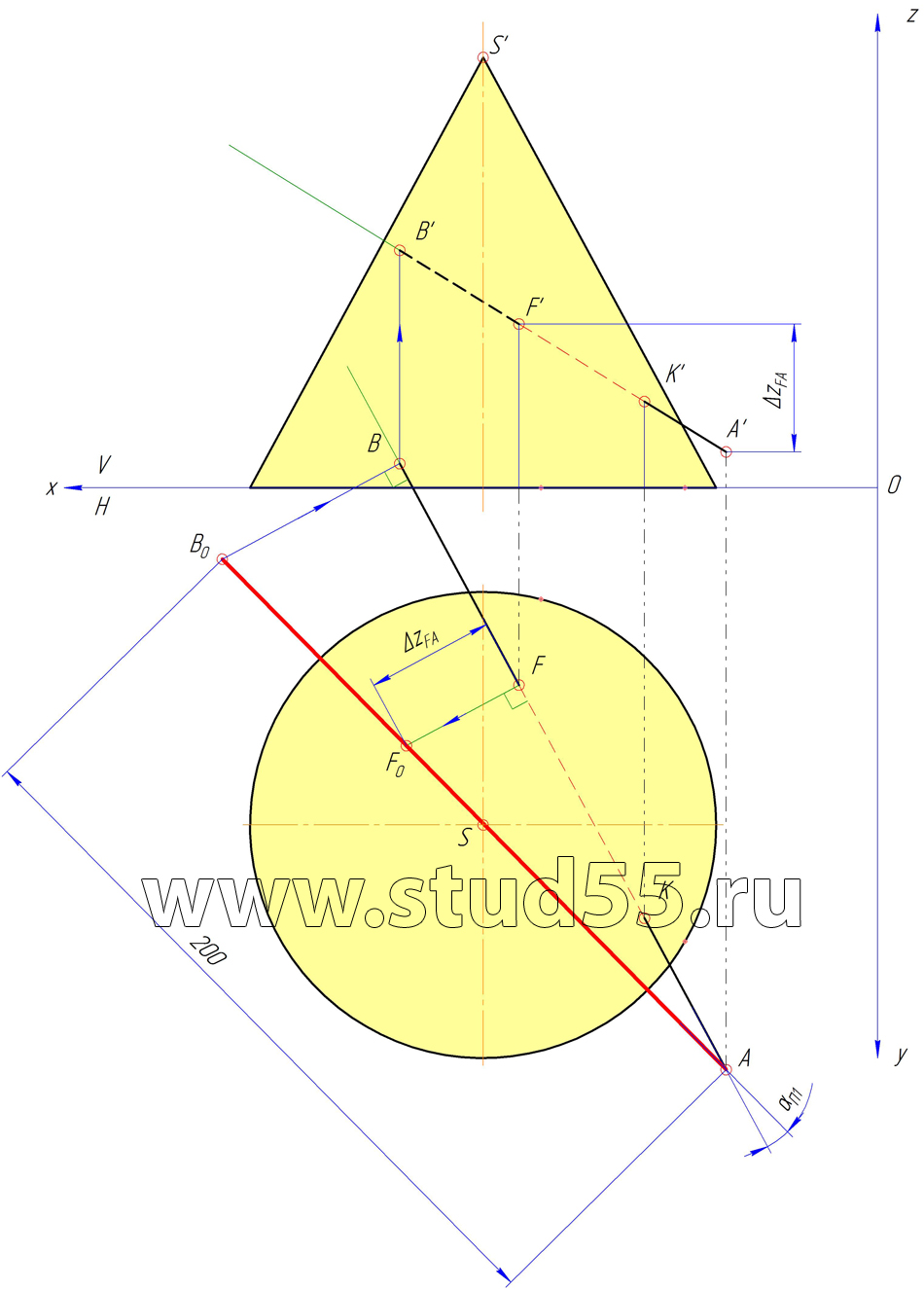
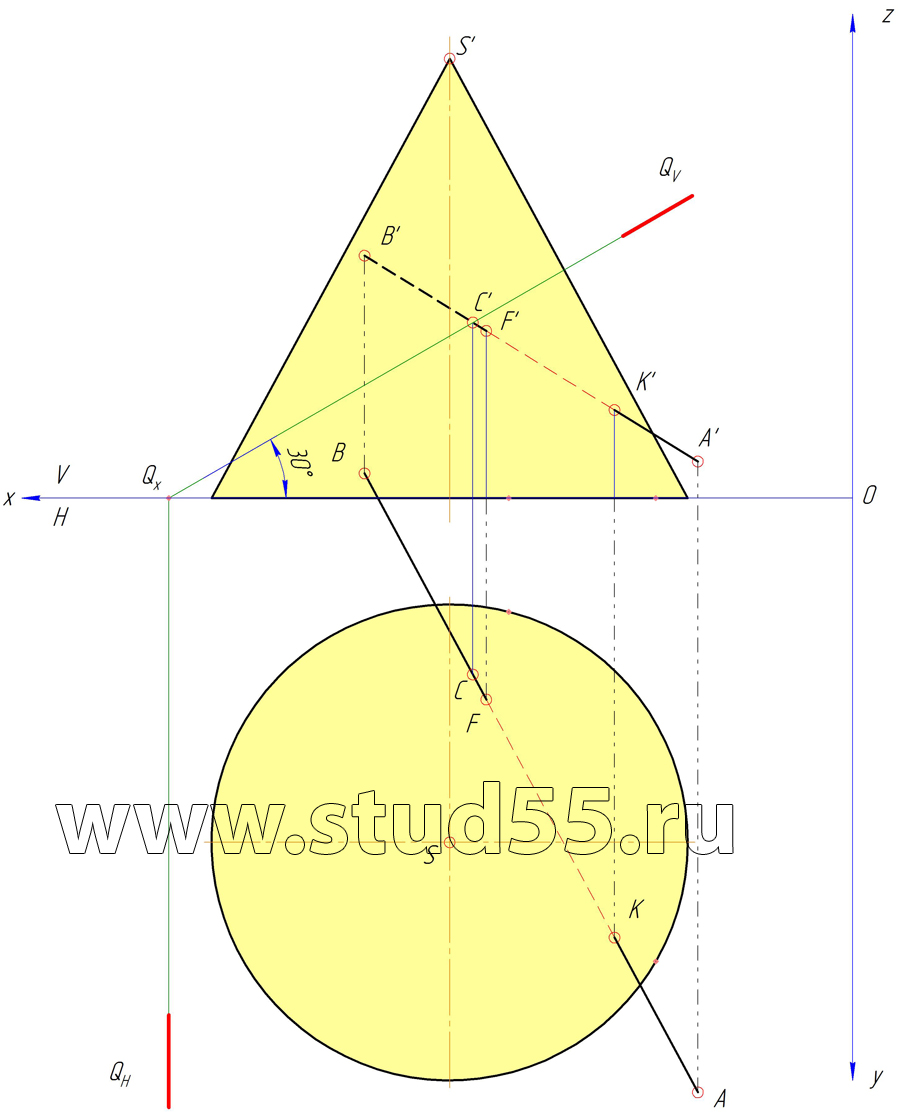
Прямой круговой конус с основанием на плоскости H (диаметр основания 130 мм) и вершиной в точке S (110;95;120) пересекаются плоскостью Q и прямой AB, заданной горизонтальными проекциями точек пересечения её с поверхностью конуса: F (100;55;-) и К (65;120;-). Длина прямой АВ равна 200 мм. Точка А находится на расстоянии 10 мм от плоскости Н.
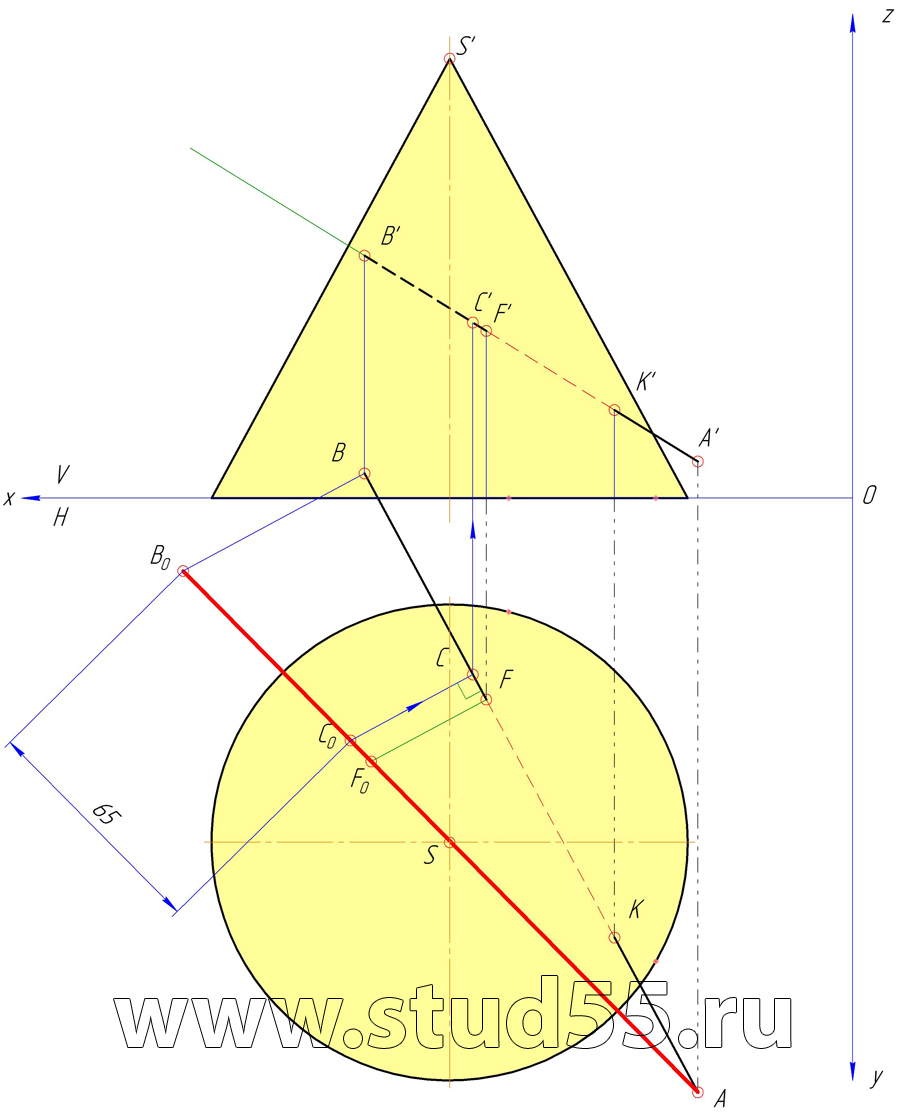
Плоскость Q наклонена к горизонтальной плоскости проекций под углом равным 30 гр. и пересекает АВ в точке С, если ВС=65 мм.
Определить
1) недостающие проекции точек F и K;
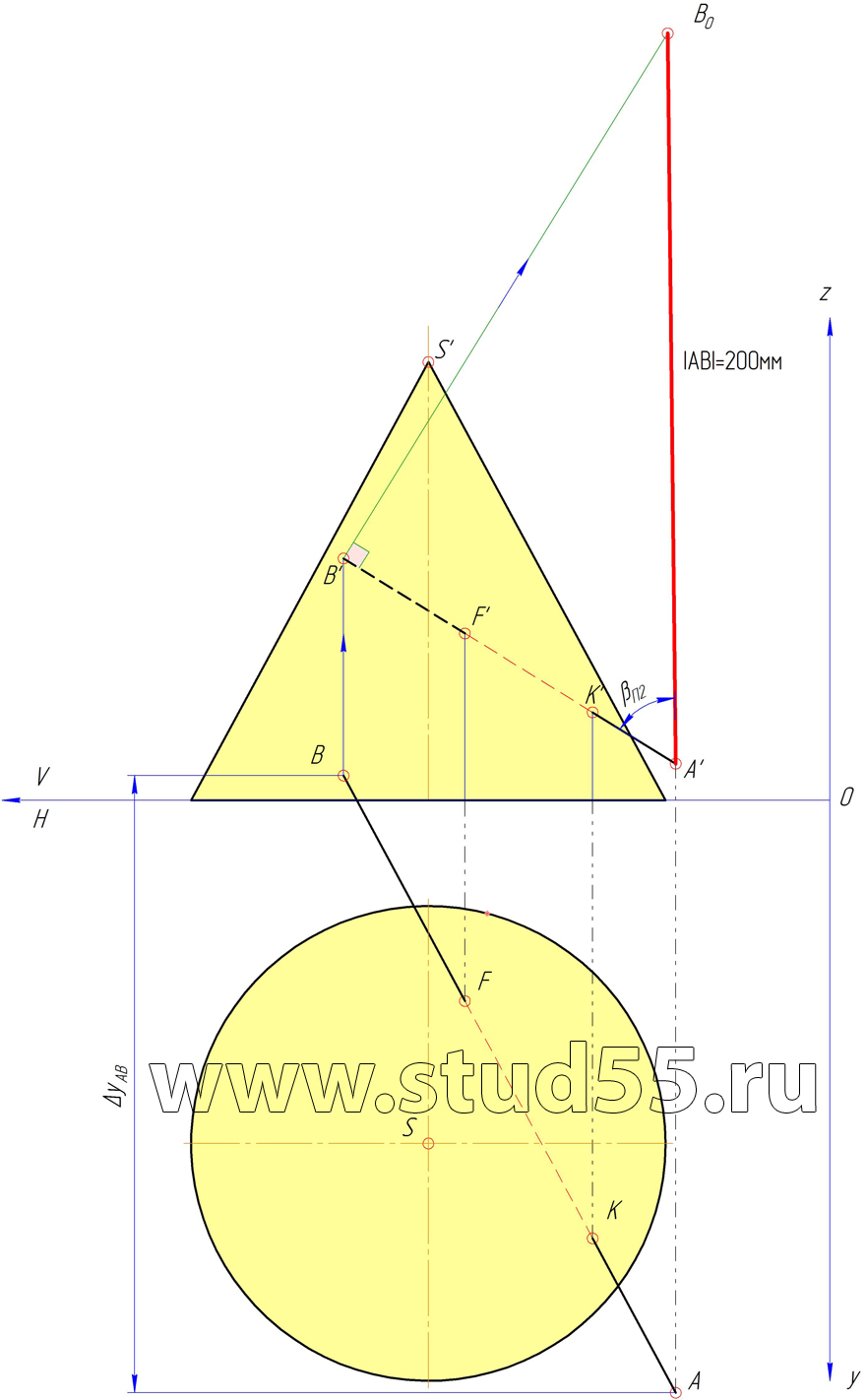
2) проекции прямой АВ и углы наклона её к фронтальной и горизонтальной плоскостям проекций;
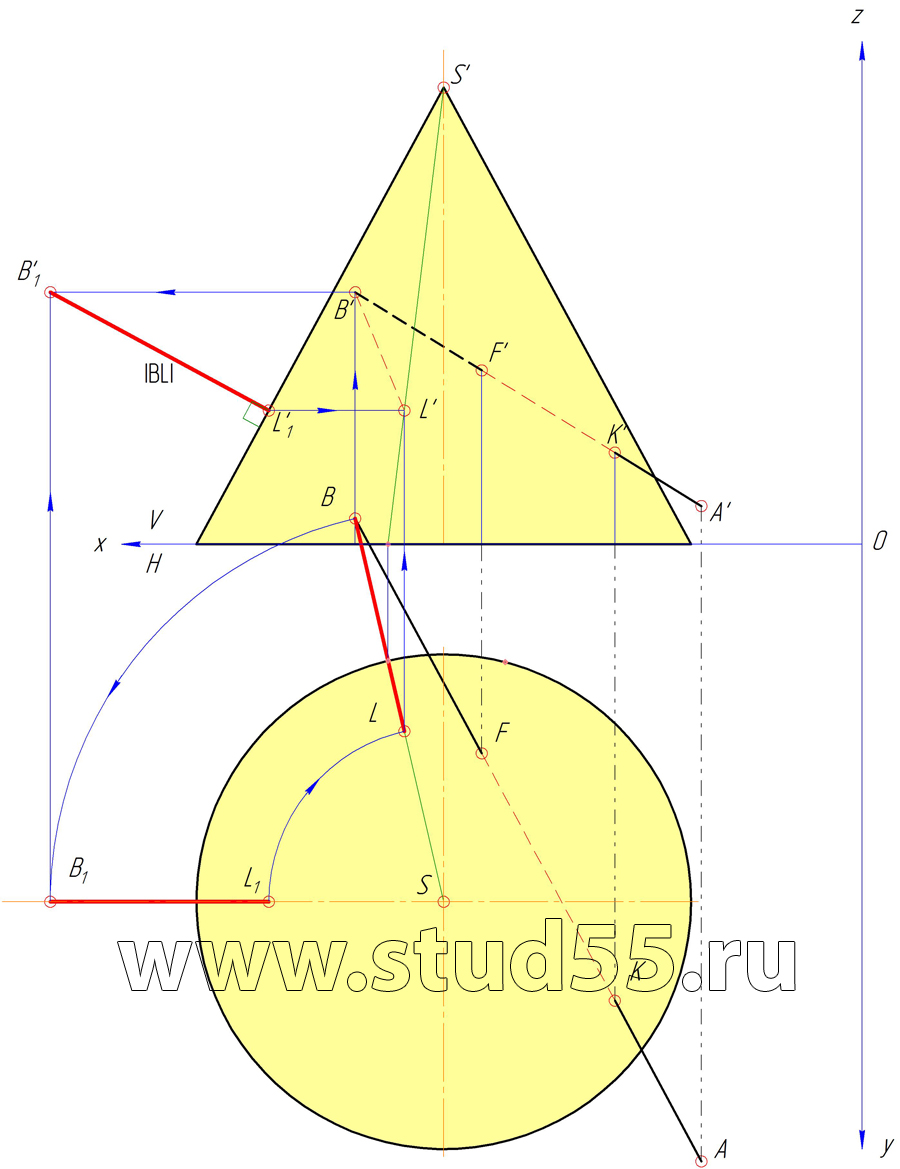
3) расстояние от точки В до поверхности конуса;
Построить
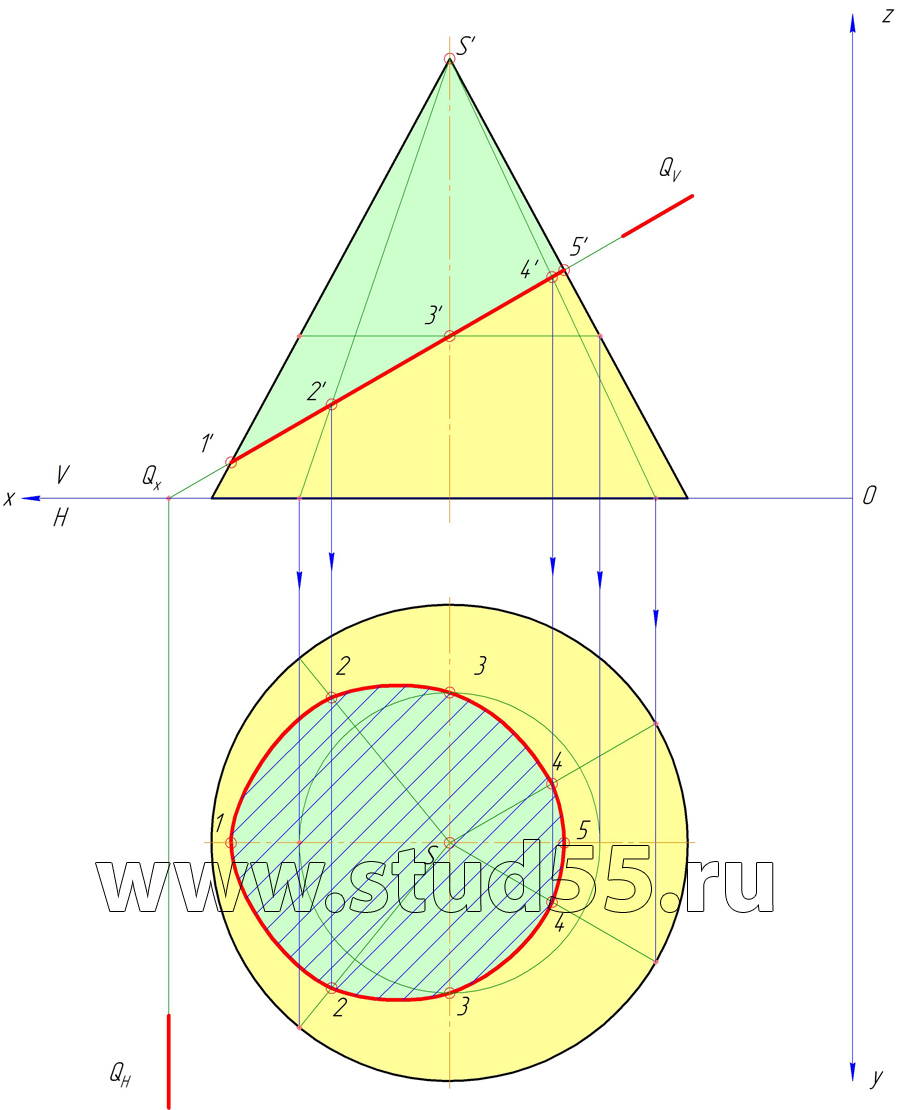
1) проекции линии пересечения конуса и плоскости Q;
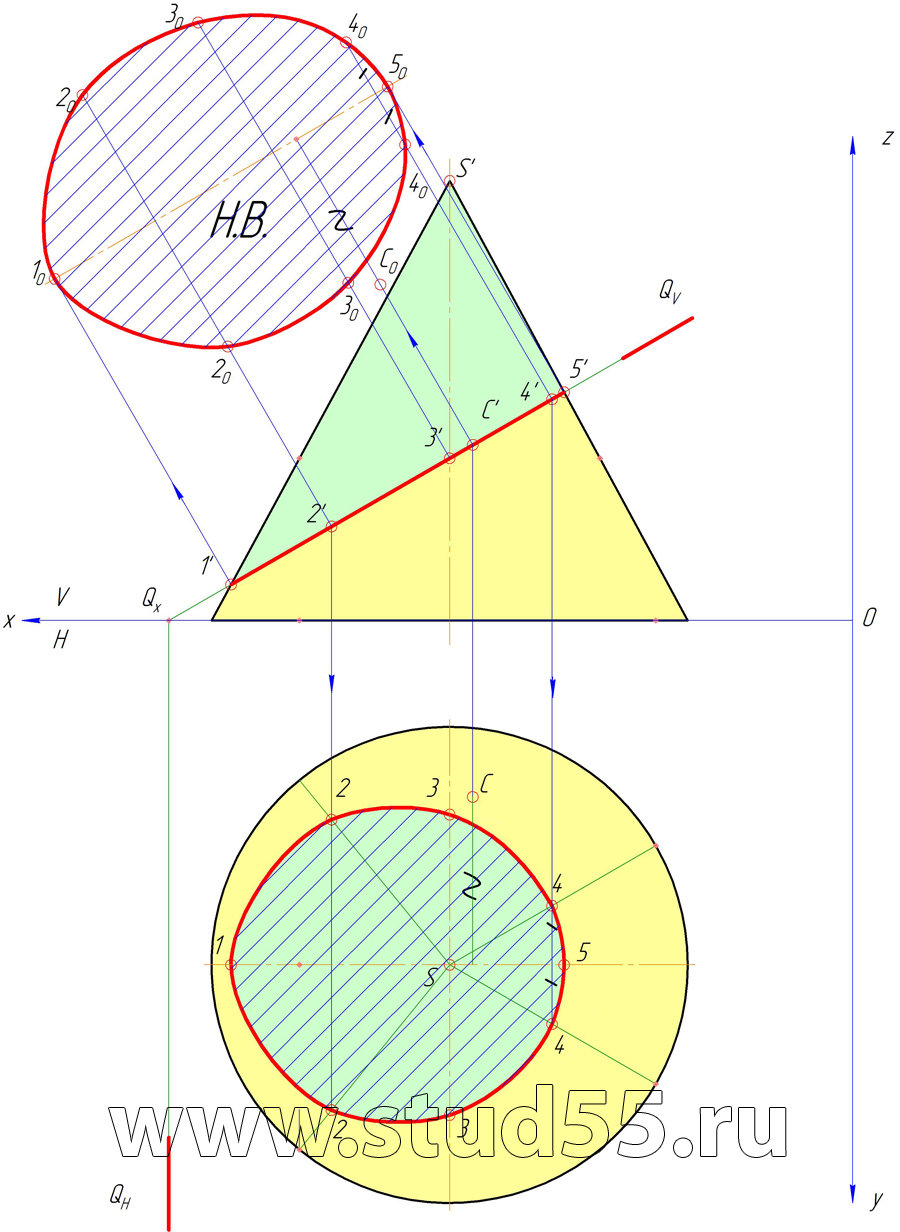
2) натуральную величину фигуры сечения с указанием точки пересечения плоскости Q и прямой АВ.
Пошаговое решение
Шаг №1 — Построение конуса по координате вершины и заданной высоте 120 мм, и горизонтальных проекций точек F и К по заданным координатам
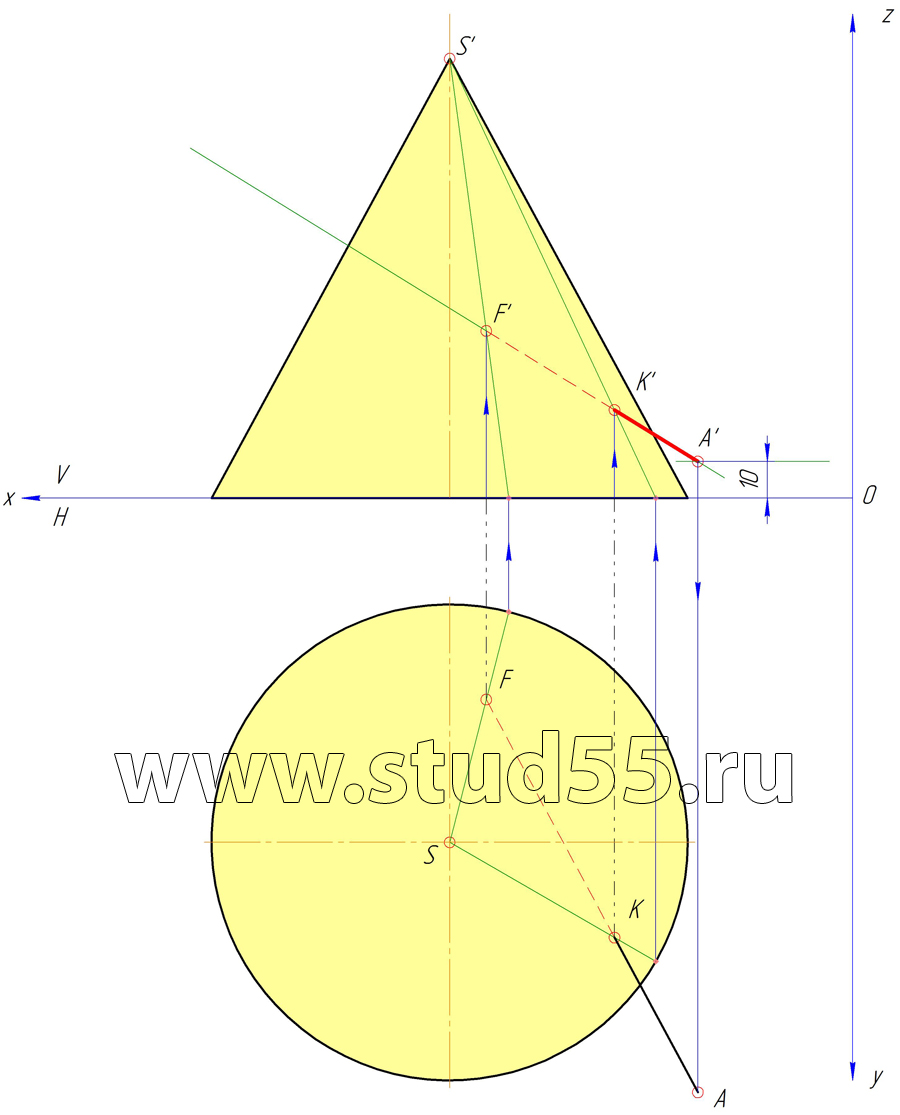
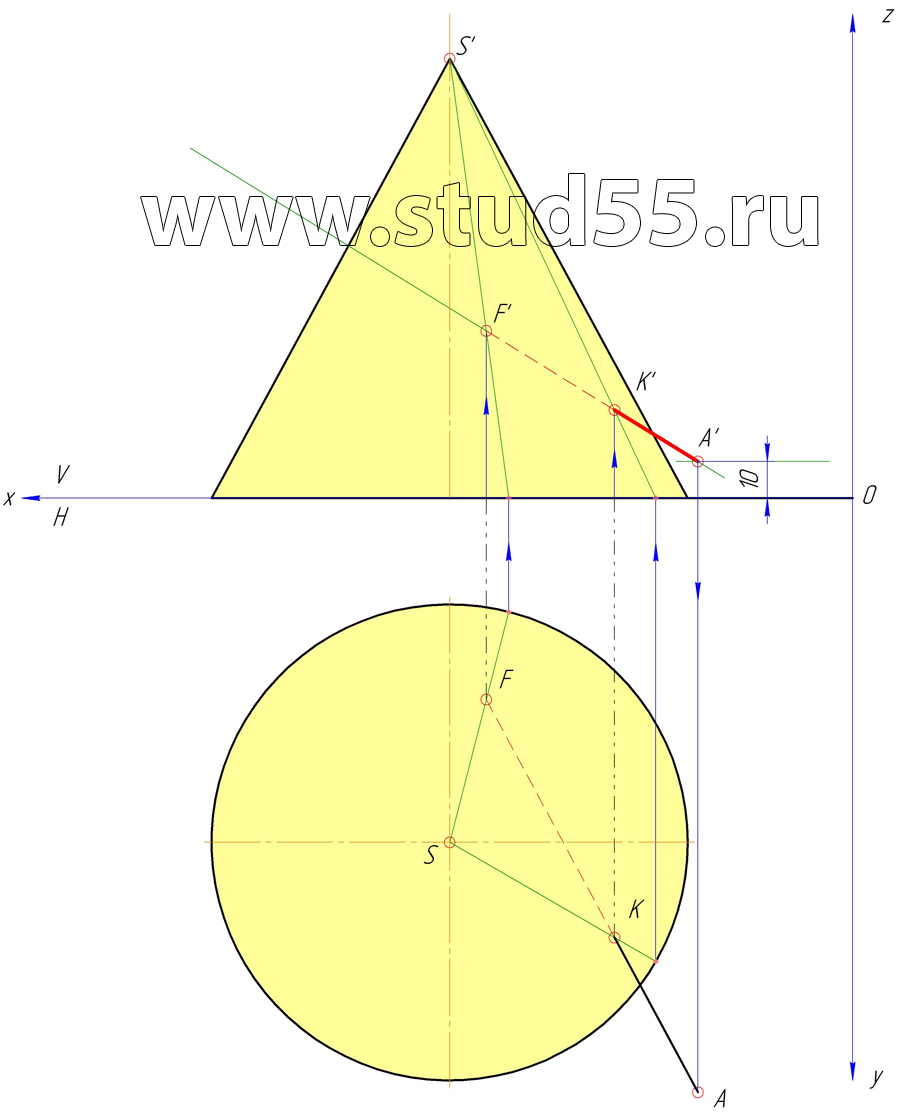
Шаг №2 — Построение точек F и K на вертикальной плоскости проекций V
Шаг №3 — Нахождение проекций точки А
Шаг №4 — Нахождение проекций точки В и угла наклона АВ к плоскости Н
Шаг №5 — Нахождение угла наклона АВ к плоскости V
Шаг №6 — Нахождение расстояния от точки В до поверхности конуса
Шаг №7 — Нахождение проекций точки С
Шаг №8 — Построение плоскости Q
Шаг №9 — Построение сечения конуса плоскостью Q в горизонтальной плоскости
Шаг №10 — Построение натуральной величины фигуры сечения
Раздел: Без рубрики /
- Рекомендуем
- Комментарии
- Наши товары
Урок по геометрии в 11 классе

Учитель МБОУ Евдокимовской средней общеобразовательной школы
Ковалева Ж. А.
Конус. Сечения конуса плоскостями.
Цель : 1.Продолжить формирование систематических сведений об основных видах тел вращения.
2. Разобрать определение конуса и подчиненных понятий : основание, вершина, образующая.
3.Рассмотреть сечения конуса , проходящие через вершину , в том числе осевые ,и перпендикулярные оси .
4. Способствовать развитию пространственного воображения учащихся.
Тип : комбинированный
Оборудование : набор геометрических тел : цилиндры, призмы, пирамиды, конусы: полные и усеченный ; предметы имеющие форму конуса или усеченного конуса.
Ход урока :
I Организационный момент : проверить готовность класса к уроку , организовать учащихся на восприятие и выполнение работы.
II Актуализация знаний учащихся :
-
Давайте повторим пройденный нами материал по геометрии, вспомним курс черчения и попробуем назвать тела, которые находятся у меня на столе (учитель показывает тело – дети его называют).
-
(Учитель показывает пузырек из – под лекарств). Сочетанием каких геометрических тел образована форма этого предмета? (ученик выходит к доске показывает и называет составные части предмета: 2 цилиндра и усеченный конус)
-
Давайте внимательно посмотрим на предметы, которые находятся у нас в классе и назовем те из них которые по форме напоминают
конус или усеченный конус. ( ведро, цветочный горшок, ведерко из – под майонеза, указка.)
III Новый материал :
Сегодня мы будем изучать конус. Подпишем тему сегодняшнего урока : « Конус » и нарисуем конус в тетрадях (учитель выполняет рисунок на доске по правилам построения изометрической проекции окружности ( рис. 442 учебника ).
1. Теперь давайте попробуем дать определение конуса. (Конусом называется тело, которое состоит из круга, точки не лежащей в плоскости этого круга и всех отрезков, соединяющих эту точку с точками круга).
Как называются составные части конуса? ( основание , вершина , образующие )
Что называют образующими конуса ? ( отрезки , соединяющие вершину конуса с точками окружности основания )
Что называется высотой конуса ? ( перпендикуляр , опущенный из его вершины на плоскость основания )
( из основания и боковой поверхности )
Так же как в школьном курсе геометрии мы рассматриваем только прямые цилиндры ,
конусы
мы будем рассматривать тоже
прямые.
( учитель показывает прямые конусы )
Какой же конус мы будем называть прямым ?
(если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания ).
Что мы можем сказать о высоте прямого конуса (основание высоты совпадает с центром основания ) , об образующих прямого конуса (равны между собой ).
Что называется осью конуса ? ( прямая , содержащая его высоту )
Параграф который мы начали изучать называется « Тела вращения » и мы уже знаем ,что прямой цилиндр можно наглядно представить как тело, получаемое при вращении какой фигуры ? ( прямоугольника около его стороны как оси ).
( вращение прямоугольного треугольника вокруг его катета как оси ).
-
Сечения
Теперь рассмотрим вопрос о сечениях конуса плоскостями.
Каким образом можно провести сечение конуса плоскостью, проходящей через его вершину
?
а) сечение проходящее через вершину конуса и не содержащее ось конуса ( разобрать по рис. 444 учебника )
Задаются вопросы
: что собой представляет это сечение ? (треугольник )
Какой треугольник и почему? ( равнобедренный , т. к. боковые стороны являются образующими конуса )
б) сечение проходящее через вершину и ось конуса. (рис. 445 учебника, рис.1 на доске ученик строит сечение и комментирует )
Вопросы :
как называется такое сечение ? ( осевое )
Что мы можем сказать об этом сечении? ( равнобедренный треугольник, где боковые стороны являются образующими конуса; основание треугольника – диаметр основания конуса )
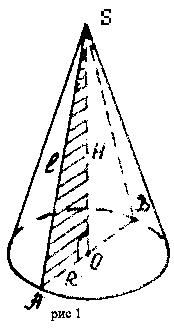 ешаются задачи по рисунку 1 ( устно )
ешаются задачи по рисунку 1 ( устно ) 9.
Радиус основания конуса 3 м, высота 4 м. Найдите образующую.
Решение: из прямоугольного треугольника по теореме Пифагора l2 = 32 + 42 = 25 ; l = 5 м
N 10
Образующая конуса l наклонена к плоскости основания под углом 300. Найдите высоту.
Решение : H= l cos 300 = l /2
12
В равностороннем конусе ( в осевом сечении правильный треугольник ) радиус основания R. Найдите площадь сечения, проведенного через две образующие, угол между которыми равен .(рис 467 учебник)
Решение : l= 2R ; S=1/2 (4R2 sin ) = 2R2 sin .
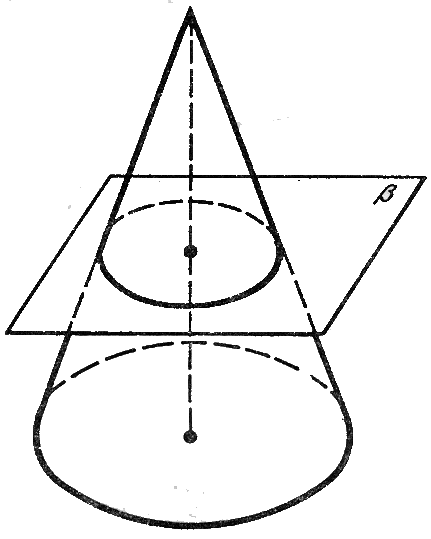
Мы рассмотрели сечения конуса плоскостями, проходящими через вершину конуса. А что будет представлять собой сечение конуса плоскостью параллельной плоскости основания конуса.
( круг ).
Давайте докажем это.
Преобразование гомотетии относительно вершины конуса совмещает сечение конуса с основанием конуса. А так как основанием конуса является круг, следовательно , это сечение тоже круг ; а сечение боковой поверхности – окружность с центром на оси конуса.
Это
Теорема 20.2
Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а боковую поверхность – по окружности с центром на оси конуса.
Задача N 15 ( разобрана в учебнике ) вызвать ученика для решения (по рис 446 учебника и рис. 2 на доске ).
Конус пересечен плоскостью, параллельной основанию, на расстоянии d от вершины. Найдите площадь сечения, если радиус основания конуса R, а высота Н.
Решение : d / H = r / R, следовательно r = Rd / H. S = R2 d2 / H2.
-
У
сеченный конус.
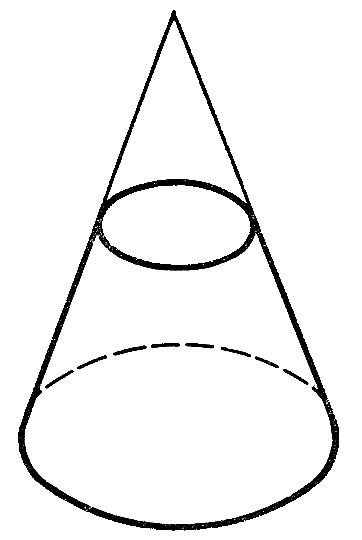
Обратите внимание, на какие две части разбивает конус плоскость параллельная основанию конуса. Рис 2.
( на меньший конус и усеченный конус )
«Учитель стирает на рисунке меньший конус, получая при этом усеченный конус.»
а) Что мы можем сказать об усеченном конусе ? ( ограничен двумя кругами – основаниями; образующие равны; высота – расстояние между плоскостями основания ; ось – ось исходного конуса ).
б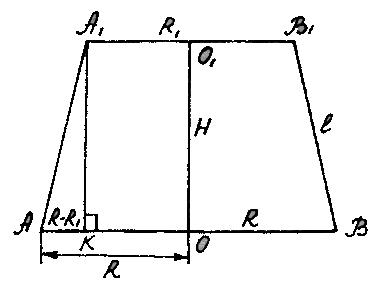
Что из себя представляет осевое сечение усеченного конуса? (равнобокая трапеция с основаниями равными диаметрам оснований усеченного конуса )
Задача :
высота усеченного конуса Н. Радиусы усеченного конуса R1 и R2 . Найдите длину образующей. ( по рис. 3 в тетрадях). «решает ученик у доски»
Решение : по теореме Пифагора :
l2= H2 +(R2–R1)2
рис.3
(эту формулу в рамочку )
Задача 19 ( устно по рис. 3) Радиусы оснований усеченного конуса 3м и 6м, высота 4м. Найдите образующую.
Решение : l2= 42+( 6-3 )2 = 16+9 = 25 ; l = 5м
Задача 21 ( письменно ученик у доски по рис. 3 ) Образующая усеченного конуса равна 2а и наклонена к основанию под углом 600. Радиус одного основания вдвое больше радиуса другого основания. Найдите каждый из радиусов.
Решение: пусть х – один радиус, тогда 2х – другой радиус. АК = АО – А1О1 = 2х – х = х. Х = 2а cos 600 = а – один радиус, 2а – другой радиус.
Задача 23 ( письменно по рис .3 ) Площади оснований усеченного конуса 4дм2 и 16дм2. Через середину высоты проведена плоскость, параллельная основаниям. Найдите площадь сечения.
Р
ешение: по теореме Фалеса получаем среднюю линию трапеции . Средняя линия трапеции ( диаметр сечения ) равна полусумме оснований , в данном случае сумме радиусов оснований. Следовательно радиус сечения равен полусумме радиусов оснований. Из формулы для площади круга находим радиусы оснований :
Sс еч. = 9 дм2
IV Итоги урока:
Давайте вспомним, а какие предметы по форме напоминающие конус или усеченный конус мы встречаем в повседневной жизни.
Выставление оценок.
V Д / З : п. 184 – 185 , N 11, N 20, N 22.
Приложение 1
Оформление доски перед началом урока

К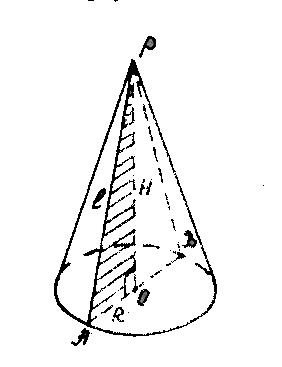
Д/з § 20 п. 184-185
№ 11, 20, 22
рис1 рис 2
Оформление доски в процессе урока

К

l2=H2+(R-R1)2
онус. Сечения конуса плоскостями.
Д/з § 20 п. 184-185
№ 11, 20, 22
№ 12
l= 2R
S=1/2 (4R2 sin ) = 2R2 sin .
Длина образующей усеченного конуса
АК=R-R1 A1K=H
по теореме Пифагора
рис1 рис 2
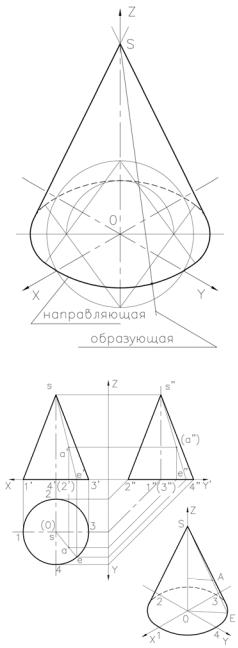
Лекция 16. ПРОЕКЦИИ КОНУСА
Конус – тело вращения.
Прямой круговой конус относится к одному из видов тел вращения.
Коническая поверхность образуется прямой линией, проходящей через некоторую неподвижную точку и последовательно через все точки некото-
рой кривой направляющей линии. Неподвижная точка S называется вершиной. Основанием конуса служит поверхность образованная замкнутой направляющей.
Конус, основанием которого является окружность, а вершина S находится на оси
перпендикулярной основанию, проходящей через его середину, называется прямым кру-
говым конусом. Рис. 1.
Построение ортогональных проекций конуса, приведено на рис. 2.
Горизонтальная проекция конуса представляет собой окружность, равную основанию конуса, а вершина конуса S совпадает с ее центром. На фронтальную и профильную проекции конус проецируется в виде треугольни-
ка, ширина основания которого равна диаметру основания. А высота равна высоте конуса. Наклонные стороны треугольника – проекции крайних (очерковых) образующих конуса.
|
Построение конуса в прямоуголь- |
||
|
ной изометрии приведено на рис. 2. |
||
|
Рис. 1 |
Построение начинаем с расположе- |
|
|
ния аксонометрических осей OX, OY, OZ, |
||
|
проведя их под углом 1200 друг к другу. Ось |
||
|
конуса направим по оси OZ, и отложим на |
||
|
ней высоту конуса, получив точку S. Прини- |
||
|
мая точку O за центр основания конуса, |
||
|
строим овал, представляющий основание |
||
|
конуса. Затем проводим две наклонные ка- |
||
|
сательные из т. S к овалу, которые будут |
||
|
крайними (очерковыми) образующими кону- |
||
|
са. Невидимую часть нижнего основания ко- |
||
|
нуса выполним штриховой линией. |
Построение точек на поверхности конуса в ортогональных и аксонометриче-
ской проекциях показано на рис. 2, 3.
Если на фронтальной проекции конуса Рис. 2 заданы точки А и В, то недостающие проек-
ции этих точек можно построить двумя способами.
Первый способ: с помощью проекций вспомогательной образующей проходящей через заданную точку.
Дано: фронтальная проекция точки А – точка (а’), расположенная в пределах видимой части конуса.
Через вершину конуса и заданную точку (a’) проводим прямую линию до основания конуса и получаем точку (e’) – основание образующей s’e’.
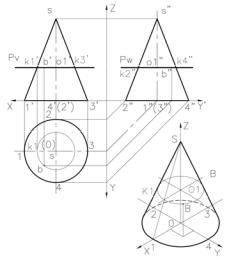
Далее строим горизонтальную проекцию этой образующей на плоскости
H. Найдем горизонтальную проекцию т. e в пределах видимой части окружности основания конуса, проведя проецирующую прямую e’e, и соединим полученную т. е с горизонтальной проекцией вер-
шины конуса s.
Так как искомая т. А принадлежит обра-
зующей s’e’ то она должна лежать на ее горизонтальной проекции. Поэтому с помощью линии связи мы переносим ее на линию se и по-
лучаем горизонтальную проекцию т. a. Профильная проекция a” т. А определя-
ется пересечением той же образующей s”e” на профильной проекции с линиями связи, переносящими т. а с горизонтальной и фронталь-
ной проекций.
Профильная проекция a” т. А в данном
случае невидимая, т. к. находится за проекцией крайней образующей s”4” и обозначается в круглых скобках.
Рис. 3 Второй способ: с помощью построения проекций сечения конической поверхности горизонтальной плоскостью Pv па-
раллельной основанию конуса и проходящей через заданную точку В. Рис. 3. Дано: фронтальная проекция точки В – т. b’, расположенная в пределах
видимой части конуса.
Через т. b’ проводим прямую, Pv параллельную основанию конуса, кото-
рая является фронтальной проекцией секущей плоскости P. Эта линия пересе-
кает ось конуса в т. 01’ и крайние образующие в т. k1’ и k3’. Отрезок прямой k1’k3’ является фронтальной проекцией сечения конуса через т. b’.
Горизонтальной проекцией этого сечения будет окружность, радиус которой определяется на фронтальной проекции как расстояние 01’k1’ от оси ко-
нуса до крайней образующей.
Так как точка b’ лежит в плоскости сечения, то с помощью линии связи переносим ее на горизонтальную проекцию сечения в пределах видимой части конуса.
Профильная проекция т. b” определяется как пересечение профильной
проекции сечения k2”k4” с линией связи, переносящей положение т. b с гори-
зонтальной проекции.
Построение точек на поверхности конуса в аксонометрии.
Строим конус в прямоугольной изометрии. Построение окружности основания конуса в аксонометрии повторяет построение основания цилиндра. (См. раздел 8.2.1.). Отложив на вертикальной оси высоту конуса, проводим две образующие – касательные к овалу основания.
Первый способ. Рис. 2.
Строим образующую SE: на оси X или Y откладываем координаты Х или
Y соответствующие т. Е на горизонтальной проекции и проведем через них линии параллельные оси Y или X соответственно. Пересечение их дает положение точки Е на основании конуса.
Соединим т. Е с вершиной конуса S и с центром основания т. 0. Рассмотрим полученный треугольник S0E: сторона 0S – ось симметрии конуса совпадающая с осью Z. Сторона SE – образующая конуса, на которой находится т. А. Сторона 0E – основание треугольника составляющая с осью Z угол 900.
Рис. 4
Высоту т. А берем на фронтальной проекции по перпендикуляру от ос-
нования конуса до т. a’ и откладываем ее в аксонометрии на оси Z, то есть на стороне 0S.
Через полученную засечку проводим прямую в плоскости треугольника
параллельно основанию треугольника до пересечения с образующей SE. Таким образом, переносим высоту положения т. А на поверхность кону-
са.
Второй способ. Рис. 3.
Строим сечение конуса плоскостью параллельной основанию и проходящей через т. В. Такое сечение конуса есть окружность с радиусом равным
отрезку ОК расположенной на высоте равной высоте т. В. В аксонометрии эта окружность строиться в виде эллипса (или заменяющего его овала).
Затем, на осях X и Y в основании конуса откладываем соответствующие
координаты X и Y т. В взятые с горизонтальной проекции и из точки их пересечения восстанавливаем перпендикуляр до пересечения с эллипсом сечения,
что определит положение т. В.
Сечения конуса.
Взависимости от направления в пространстве секущей плоскости, проходящей через конус, в сечении прямого кругового конуса могут получаться
различные плоские фигуры:
А – прямые (образующие) Б – гипербола
В– окружность
Г – парабола
Д – эллипс Конические сечения – эллипс, парабола и гипербола являются лекаль-
ными кривыми, которые строятся по точкам принадлежащим кривой сечения.
А. Сечение конуса вертикальной плоскостью проходящей через его вершину представляет собой прямые. Рис. 4.
На горизонтальной проекции конуса через точку S проводим линию Ph под произвольным углом к осям X и Y, которая является горизонтальной проекцией секу-
щей вертикальной плоскости. Эта линия
пересекает окружность основания конуса в двух точках a и b, а отрезок aob является горизонтальной проекцией сечения конуса.
Мысленно отбросим левую часть конуса от линии Ph и справа от нее получим горизонтальную проекцию усеченного ко-
нуса.
Отрезки SA и SB – горизонтальные
проекции образующих конуса, по которым и проходит секущая плоскость Ph.
Строим образующие SA и SB на
фронтальной проекции, перенеся на нее точки A и B и соединив полученные точки a’ и b’ с вершиной s’. Треугольник a’s’b’ и будет фронтальной проекцией сечения
конуса, а линия s’3’ – крайней образующей конуса.

Рис. 5
Аналогично строим профильную проекцию сечения конуса, перенеся
точки a и b с горизонтальной проекции на профильную и соединив полученные точки a” и b” с вершиной конуса s”. Треугольник a”s”b” является профильной проекцией сечения конуса, а линия s”2” есть крайняя образующая конуса.
Построение аксонометрии. Рис. 4.
Строим конус в аксонометрии, как описано выше.
Далее с горизонтальной проекции конуса берем координаты по оси X или Y для точек A и B и переносим их на аксонометрические оси X или Y. Через полученные точки проводим вспомогательные линии параллельные осям Y
или X соответственно. Их пересечение с линией основания конуса позволяет получить точки A и B на аксонометрии. Соединив их между собой, и каждую из
них с вершиной конуса S, получим треугольник ABS являющийся сечением конуса вертикальной плоскостью P.
Б. Сечение конуса вертикальной плоскостью, не проходящей через его вершину, представляет собой гиперболу. Рис. 5.
Строим три проекции конуса – горизонтальную, фронтальную и про-
фильную.
Если вертикальная секущая плоскость P не проходит через вершину конуса, то она уже не совпадает с образующими его боковой поверхности, а наоборот – пересекает
их.
На горизонтальной проекции конуса проводим секущую плоскость Ph на произвольном расстоянии от вершины S и парал-
лельную оси Y. В общем случае положение
секущей плоскости относительно осей X и Y может быть любое.
Линия Ph пересекает окружность основания конуса в двух точках a и b. Отрезок ab этой прямой есть горизонтальная проек-
ция сечения конуса. Часть окружности слева от линии Ph делим на произвольное коли-
чество равных частей, в донном случае на 12 и, затем каждую полученную точ-
ку на окружности соединяем с вершиной конуса s. Эти образующие пересека-
ются секущей плоскостью Ph и мы получаем ряд точек, которые принадлежат образующим и проекции сечения конуса ab одновременно.
Строим полученные образующие на фронтальной проекции конуса
.Переносим с горизонтальной проекции все точки на основании конуса (a, 1, …,
5, b) и на фронтальной проекции получаем точки (a’, 1’, …, 5’, a’) и соединяем из с вершиной конуса s’. Проводим на фронтальной проекции через точку b’ секущую плоскость Pv перпендикулярно основанию конуса. Линия Pv пересекает
все образующие, и точки их пересечения принадлежат проекции сечения конуса.
Повторим построение всех образующих на профильной проекции конуса, перенеся на нее точки (a, 1, …, 5, b) с горизонтальной проекции. Полученные точки (a”, 1”, …, 5”, b”) соединим с вершиной s”.
На полученные образующие перенесем с фронтальной проекции точки пересечения соответствующих образующих с секущей плоскостью Pv. Полученные точки соединим кривой линией, которая представляет собой лекальную
кривую – гиперболу.
Построение аксонометрии. Рис. 5.
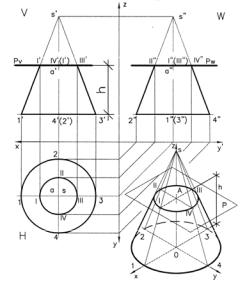
Рис. 6
Строим конус в аксонометрии, как описано выше.
Далее с горизонтальной проекции конуса берем координаты по оси X или Y для всех точек a, 1, …, 5, b и переносим их на аксонометрические оси X или Y находим их положение на основании конуса в аксонометрии. Соединяем
их последовательно с вершиной конуса S и получаем ряд образующих на поверхности конуса соответствующих образующим на ортогональных проекциях.
На каждой образующей найдем точку ее пересечения с секущей плоскостью P аналогично тому, как это было описано выше (см. построение точек на поверхности конуса, первый способ).
Соединив полученные на образующих точки лекальной кривой, а также точки A и B получим аксонометрическую проекцию усеченного конуса.
В Сечение конуса горизонтальной плоскостью. Рис. 6.
Сечение прямого кругового конуса горизонтальной плоскостью параллельной основанию – есть окружность.
Если рассечь конус на произвольной высоте h от основания конуса через точку a’
лежащую на его оси o’s’ плоскостью параллельной его основанию, то на фронтальной проекции мы увидим горизонтальную линию Pv являющуюся фронтальной проекцией секущей плоскости, которая образует сечение
конуса I’, II’, III’, IV’. На профильной проекции
W вид секущей плоскости и сечение конуса аналогичен и соответствует линии Pw.
На горизонтальной проекции сечение
конуса представляет собой круг в натураль-
ную величину, радиус окружности которого проецируется с фронтальной проекции как расстояние от оси конуса в точке a’ до точки I’, лежащей на крайней образующей 1’s’.
Построение аксонометрии. Рис. 6.
Строим конус в аксонометрии, как опи-
сано выше.
Затем на оси Z откладываем высоту h точки А от основания конуса. Через точку А проводим линии параллельные осям X и Y и строим окружность в
аксонометрии радиусом R=a’I’ взятым с фронтальной проекции.
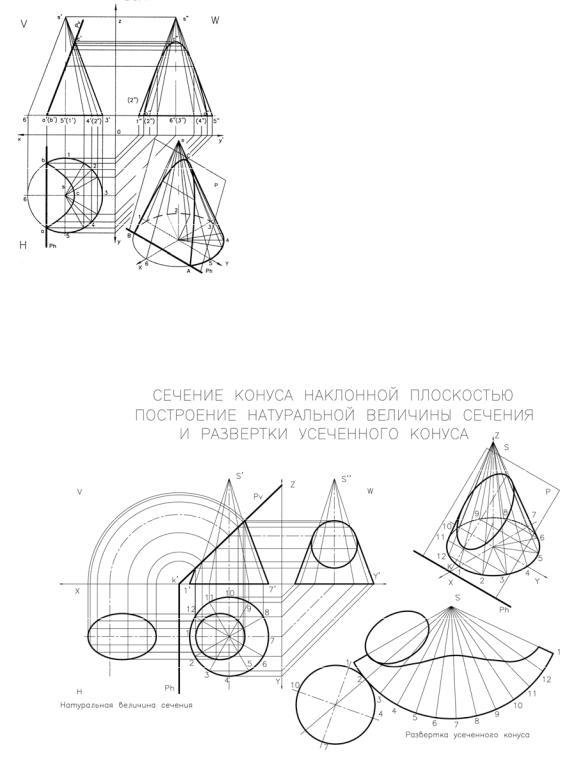
Г Сечение конуса наклонной плоскостью, параллельной образующей. Рис. 7.
Строим три проекции конуса – горизонтальную, фронтальную и профильную. (см. выше).
На фронтальной проекции конуса проводим секущую плоскость Pv параллельно очерковой образующей s’6’на произвольном расстоянии от ее нача-
ла на основании конуса через т. a’(b’). Отрезок a’c’ есть фронтальная проекция сечения конуса.
На горизонтальной проекции строим проекцию основания секущей плоскости Р через точки a, b. Отрезок ab – есть проекция основания сечения конуса.
Далее окружность основания конуса делим на произвольное количество частей и полученные точки соединяем с вершиной конуса s. Получаем ряд образующих конуса, которые последовательно переносим на фронтальную и профильную проекции. (см. пункт Б).
На фронтальной проекции след секущей плоскости Pv пересекает обра-
зующие и в пересечении дает ряд точек, которые принадлежат как секущей плоскости, так и образующим конуса одновременно.
Переносим линиями связи эти точки на проекции образующих на гори-
зонтальную и профильную проекции.
Полученные точки соединим кривой линией, которая представляет собой
лекальную кривую – параболу.
Построение аксонометрии. Рис. 7.
Строим аксонометрическую проекцию конуса, как описано выше.
Далее с горизонтальной проекции конуса берем координаты по оси X или Y для
всех точек (a, b, 1, …, 6) и переносим их на аксонометрические оси X или Y соответственно, определив, таким образом их поло-
жение на основании конуса в аксонометрии. Соединяем их последовательно с вершиной
конуса S и получаем ряд образующих на поверхности конуса, соответствующих образующим на ортогональных проекциях.
На каждой образующей найдем точку ее пересечения с секущей плоскостью P
аналогично тому, как это было описано выше (см. построение точек на поверхности конуса).
|
Соединив полученные на образующих |
||
|
Рис. 7 |
||
|
точки лекальной кривой, а также точки A и B |
||
|
получим сечение конуса в виде параболы. |
||
Д. Сечение конуса наклонной плоскостью, расположенной под произвольным углом к основанию конуса представляет собой эллипс. Рис. 8.
Рис. 8
Строим три проекции конуса – горизонтальную, фронтальную и про-
фильную. (см. выше).
На фронтальной проекции конуса проводим линию секущей плоскости Pv под произвольным углом к основанию конуса.
На горизонтальной проекции, окружность основания конуса делим на произвольное количество равных частей ( в данном случае на 12) и получен-
ные точки соединяем с вершиной конуса S. Получаем ряд образующих, которые с помощью линий связи, последовательно переносим на фронтальную и профильную проекции.
На фронтальной проекции секущая плоскость Pv пересекает все образующие, и полученные точки их пересечения принадлежат одновременно и се-
кущей плоскости и боковой поверхности конуса, являясь фронтальной проекцией искомого сечения.
Переносим эти точки на горизонтальную проекцию конуса.
Затем строим и профильную проекцию сечения конуса (см. выше), соединяя полученные точки лекальной кривой, которая представляет собой эл-
липс.
Построение натуральной величины сечения.
Лекальные кривые (эллипсы) на горизонтальной и профильной проекции представляют собой искаженные изображения сечения конуса.
Истинная (натуральная) величина сечения получается путем совмеще-
ния секущей плоскости P с горизонтальной плоскостью проекций H. Все точки сечения конуса на фронтальной проекции переносим на ось X при помощи циркуля, поворачивая их вокруг точки k’. Далее, на горизонтальной проекции, линиями связи, параллельными оси Y продолжаем их до пересечения их с ли-
ниями связи, взятыми с горизонтальной проекции соответствующих точек. Пе-
ресечение горизонтальных и вертикальных линий связи соответствующих точек позволяет получить точки, принадлежащие натуральной величине сечения. Соединив их лекальной кривой, мы получим эллипс натуральной величины сечения конуса.
Построение аксонометрии усеченного конуса. Рис. 8.
Построение аксонометрии усеченного конуса выполняется путем нахождения точек принадлежащих сечению конуса любым из описанных выше способов (см. выше).
Построение развертки поверхности усеченного конуса. Рис. 8.
Предварительно построим развертку боковой поверхности не усеченного
конуса. Задаемся положением т. S на листе и проводим из нее дугу радиусом равным натуральной величине длины образующей конуса (например, s’1’или s’7’). Задаемся положением т. 1 на этой дуге. Последовательно откладываем от нее столько одинаковых отрезков (хорд) на сколько частей разделена окружность основания конуса. Полученные на дуге точки 1, 2, …, 12, 1 соединяем с т. S. Сектор 1S1 представляет собой развертку боковой поверхности не усе-
ченного конуса. Пристроив к ней в нижней части (например, к т. 2) натуральную величину основания конуса в виде круга взятого с горизонтальной проекции мы
получим полную развертку не усеченного конуса.
Для построения развертки боковой поверхности усеченного конуса необходимо определить натуральную величину всех усеченных образующих. На
фронтальной проекции все точки сечения перенесем на очерковую образующую s’7’ линиями параллельными основанию конуса. Затем каждый отрезок образующей от т. 7’ до соответствующей точки сечения переносим на соответствующую образующую на развертке. Соединив эти точки на развертке, получим кривую линию, соответствующую линии сечения боковой поверхности ко-
нуса.
Затем к линии сечения на развертке (например, к образующей S1) при-
страиваем эллипс натуральной величины сечения полученный на горизонтальной проецирующей плоскости Н.
Развертки поверхности геометрических тел представляют собой чертежи
– выкройки из бумаги и служат для выполнения макета фигуры.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

Сечение конуса — задание в инженерной графике, являющееся одной из часто используемых задач на построение. Я опишу более подробно каждый свой шаг, прикладывая рисунки. Также Вы можете посмотреть видео.
- У вас есть задание на построение сечения конуса с всеми размерами. ( для примера использовал это задание)
2. Чертим оси и строим 3 вид конуса ( вид слева). Указываем плоскость сечения конуса (зачастую ее располагают под произвольным углом)
3. Воспользуемся методом вспомогательных секущих плоскостей (они необходимы для детального построения сечения конуса). Расстояние между секущими плоскостями берем произвольно.
4. Находим вид сечения на нижнем рисунке (виде сверху)
5. Затем определим точки на виде слева.
6. Все точки найдены, приступаем обводить полученную фигуру линиями чертежа.
7. Не забываем пронумеровывать каждую точку полученного сечения.
Просмотрели 1 461





 сеченный конус.
сеченный конус. 2. Чертим оси и строим 3 вид конуса ( вид слева). Указываем плоскость сечения конуса (зачастую ее располагают под произвольным углом)
2. Чертим оси и строим 3 вид конуса ( вид слева). Указываем плоскость сечения конуса (зачастую ее располагают под произвольным углом) 3. Воспользуемся методом вспомогательных секущих плоскостей (они необходимы для детального построения сечения конуса). Расстояние между секущими плоскостями берем произвольно.
3. Воспользуемся методом вспомогательных секущих плоскостей (они необходимы для детального построения сечения конуса). Расстояние между секущими плоскостями берем произвольно. 4. Находим вид сечения на нижнем рисунке (виде сверху)
4. Находим вид сечения на нижнем рисунке (виде сверху) 5. Затем определим точки на виде слева.
5. Затем определим точки на виде слева. 6. Все точки найдены, приступаем обводить полученную фигуру линиями чертежа.
6. Все точки найдены, приступаем обводить полученную фигуру линиями чертежа. 7. Не забываем пронумеровывать каждую точку полученного сечения.
7. Не забываем пронумеровывать каждую точку полученного сечения.
