Движение тела, брошенного вертикально вверх
Тело, брошенное вертикально вверх, движется равномерно замедленно с начальной скоростью u0 и ускорением
a = -g.
Перемещение тела за время t представляет собой высоту подъема h.
Для этого движения справедливы формулы:
Если:
u0 — начальная скорость движения тела ,
u — скорость падения тела спустя время t,
g — ускорение свободного падения, 9.81 (м/с²),
h — высота на которую поднимется тело за время t,
t — время,
То, движение тела, брошенного вертикально вверх описывается следующими формулами:
Высота подъема тела за некоторое время, зная конечную скорость
[ h = frac{u_0 + u}{2} t ]
Высота подъема тела за некоторое время, зная ускорение свободного падения
[ h = u_0 t – frac{g t^2}{2} ]
Скорость тела через некоторое время, зная ускорение свободного падения
[ u = u_0 – gt ]
Скорость тела на некоторой высоте, зная ускорение свободного падения
[ u = sqrt{ u_0^2 – 2gh} ]
Максимальная высота подъема тела, зная первоначальную скорость и ускорение свободного падения
Тело, брошенное вертикально вверх, достигает максимальной высоты в тот момент, когда его скорость обращается в ноль. Поднявшись на максимальную высоту тело начинает свободное падение вниз.
[ h_{max} = frac{u_0^2}{2g} ]
Время подъема на максимальную высоту подъема тела, зная первоначальную скорость и ускорение свободного падения
[ t_{hmax} = frac{u_0}{g} ]
Примечание к статье: Движение тела, брошенного вертикально вверх
- Сопротивление воздуха в данных формулах не учитывается.
- Ускорение свободного падения имеет приведенное значение (9.81 (м/с²)) вблизи земной поверхности. Значение g на других расстояниях от поверхности Земли изменяется!
Движение тела, брошенного вертикально вверх |
стр. 409 |
|---|
Если тело бросить вертикально вверх при наличии начальной скорости υ0, оно будет двигаться равнозамедленно с ускорением, равным a=-g=-9,81υc2.
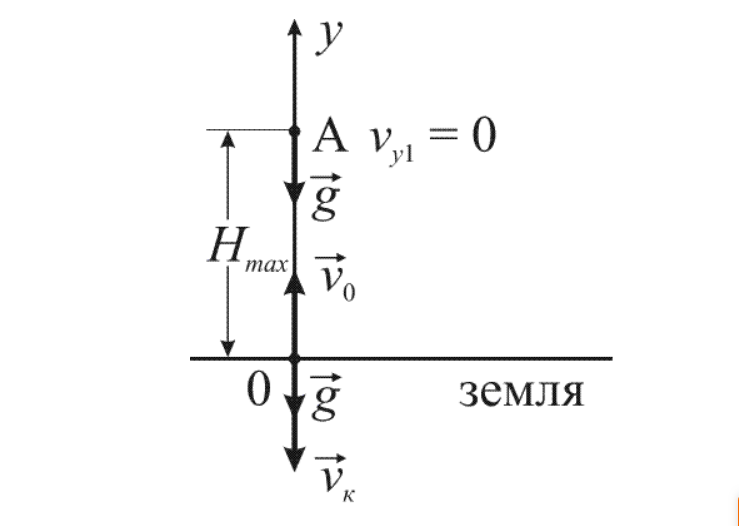
Рисунок 1
Формулы вычисления показателей движения брошенного тела
Высота подбрасывания h за время t и скорость υ через промежуток t можно определить формулами:
tmax – это время, за которое тело достигает максимальной высоты hmax=h, при υ=0, а сама высота hmax может быть определена при помощи формул:
Когда тело достигает высоты, равной hmax, то оно обладает скоростью υ=0 и ускорением g. Отсюда следует, что тело не сможет оставаться на этой высоте, поэтому перейдет в состояние свободного падения. То есть, брошенное вверх тело – это равнозамедленное движение, при котором после достижения hmax изменяются знаки перемещения на противоположные. Важно знать, какая была начальная высота движения h0. Общее время тела примет обозначение t, время свободного падения – tп, конечная скорость υк, отсюда получаем:
Если тело брошено вертикально вверх от уровня земли, то h0=0.
Время, необходимое для падения тела с высоты, куда предварительно было брошено тело, равняется времени его подъема на максимальную высоту.
Так как в высшей точке скорость равняется нулю видно:
Конечная скорость υк тела, брошенного от уровня земли вертикально вверх, равна начальной скорости υ0 по величине и противоположна по направлению, как показано на ниже приведенном графике.
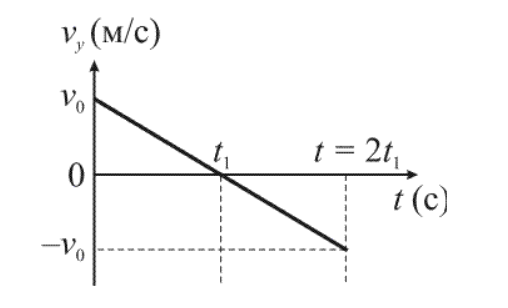
Рисунок 2
Примеры решения задач
Тело было брошено вертикально вверх с высоты 25 метров со скоростью 15 м/с. Через какой промежуток времени оно достигнет земли?
Дано: υ0=15 м/с, h0=25 м, g=9,8 м/с2.
Найти: t.
Решение
t=υ0+υ02+gh0g=15+152+9,8·259,8=3,74 с
Ответ: t=3,74 с.
Был брошен камень с высоты h=4 вертикально вверх. Его начальная скорость равняется υ0=10 м/с. Найти высоту, на которую сможет максимально подняться камень, его время полета и скорость, с которой достигнет поверхности земли, пройденный телом путь.
Дано: υ0=10 м/с, h=4 м, g=9,8 м/с2.
Найти: H, t, v2, s.
Решение
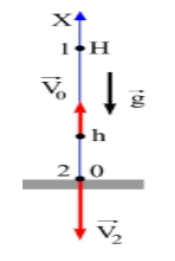
Рисунок 3
H=h0υ022g=4+1029,8=14,2 м.
t=υ0+υ02+gh0g=10+102+9,8·49,8=1,61 с.
υ2=υk=2gH=2·9,8·14,2=16,68 м/с.
s=H-h0+H=2H-h0=2·14,2=24,4 м.
Ответ: H=14,2 м; t=1,61 с; v2=16,68 м/с; s=24,4 м.
1. Формулы максимальной высоты и времени за которое тело поднялось на максимальную высоту
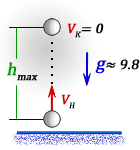
h max
– максимальная высота достигнутая телом за время t
Vк – конечная скорость тела на пике, равная нулю
Vн – начальная скорость тела
t – время подъема тела на максимальную высоту h
g ≈ 9,8 м/с2 – ускорение свободного падения
Формула максимальной высоты (h max):
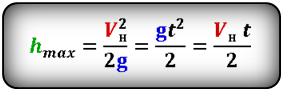
Формула времени за которое тело достигло максимальную высоту (t):
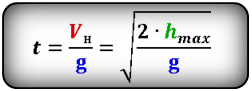
2. Формулы скорости, высоты и времени тела брошенного вертикально вверх под воздействием силы тяжести
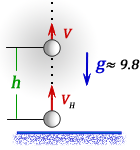
h – расстояние пройденное телом за время t
Vн – начальная скорость тела
V – скорость тела в момент времени t
t – время подъема за которое тело пролетело расстояние h
g ≈ 9,8 м/с2 – ускорение свободного падения
Формула скорости тела в момент времени t (V):
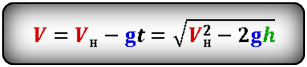
Формула начальной скорости тела (Vн):
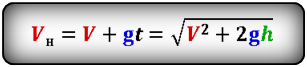
Формулы высоты тела в момент времени t (h):
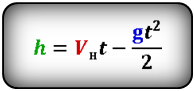
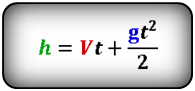
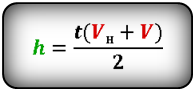
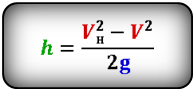
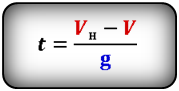
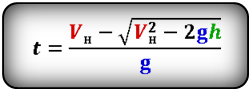
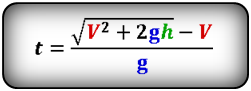
Формулы времени, за которое тело достигло высоту h (t):
- Подробности
-
Опубликовано: 04 августа 2015
-
Обновлено: 13 августа 2021
Согласно второму закону Ньютона, сила тяжести, обусловленная гравитационным притяжением, действует на все тела на поверхности Земли и вблизи неё вне зависимости от того, покоятся они или движутся.
При свободном падении тело движется равноускоренно. Это значит, что скорость свободно падающего тела увеличивается при приближении к поверхности Земли. Этому способствует ускорение свободного падения (рис. (1)).

Рис. (1)
Если подбросить тело вверх, то при отсутствии сопротивления воздуха, тело будет двигаться только под действием силы тяжести (рис. (2)), которая направлена вниз (к центру Земли). В эту же сторону направлено и ускорение свободного падения.
Начальная скорость тела при броске
υ0
направлена вверх. В результате скорость тела уменьшается до нуля (состояние «верхняя точка траектории») в соответствии с формулой
v=v0−gt
, т.е. на (9,8) м/с каждую секунду.

Рис. (2)
Обрати внимание!
Чем большую начальную скорость получило тело при броске, тем больше будет время подъёма, и тем на большую высоту оно поднимется к моменту остановки.
После того как тело поднялось на наибольшую высоту, оно под действием силы тяжести начинает равноускоренно падать вниз.
Вдоль оси (Oy) тело движется равноускоренно с ускорением свободного падения
gy
и начальной скоростью
υ0
.
Скорость изменяется с течением времени:
υy=υ0y+gyt
.
Путь, пройденный телом:
sy=υ0yt+gyt22
.
Обрати внимание!
При движении вверх с начальной скоростью
υ0
значение скорости будет уменьшаться, тело будет замедляться. Направления проекций скорости и ускорения свободного падения на ось (Oy) будут противоположными.
Пусть ось (Oy) направлена вертикально вверх, то есть сонаправлена с вектором скорости.
Тогда
(где (vec{upsilon}) — вектор скорости движения, a (vec{g}) — вектор ускорения).
Если же ось (Oy) направлена вертикально вниз, то
Если некоторое тело будет свободно падать на Землю, то при этом оно будет совершать равноускоренное движение, причем скорость будет возрастать постоянно, так как вектор скорости и вектор ускорения свободного падения будут сонаправлены между собой.
Если же подбросить некоторое тело вертикально вверх и при этом считать, что сопротивление воздуха отсутствует, то можно считать, что оно тоже совершает равноускоренное движение с ускорением свободного падения, которое вызвано силой тяжести. Только в этом случае скорость, которую мы придали телу при броске, будет направлена вверх, а ускорение свободного падения направлено вниз, то есть они будут противоположно направлены друг к другу. Поэтому скорость будет постепенно уменьшаться.
Через некоторое время наступит момент, когда скорость станет равняться нулю. В этот момент тело достигнет своей максимальной высоты и на какой-то момент остановится. Очевидно, что, чем большую начальную скорость мы придадим телу, тем на большую высоту оно поднимется к моменту остановки.
Далее, тело начнет равноускоренно падать вниз под действием силы тяжести.
Формулы для равноускоренного движения применимы для движения тела, брошенного вверх. V0 всегда > 0
Движение тела, брошенного вертикально вверх, является прямолинейным движением с постоянным ускорением. Если направить координатную ось OY вертикально вверх, совместив начало координат с поверхностью Земли, то для анализа свободного падения без начальной скорости можно использовать формулу (y = y_0+v_0yt+frac{a_yt^2}{2}),
положив (υ_0 >0, y_0 = 0, y=H, a = –g.) Или (H=y_0+v_{0y}t-frac{gt^2}2).
Вблизи поверхности Земли, при условии отсутствия заметного влияния атмосферы скорость тела, брошенного вертикально вверх, изменяется во времени по линейному закону: (v=v_0-gt), если тело поднялось на максимальную высоту, то (v=0), а (v=v_0-gt).
Скорость тела на некоторой высоте h можно найти по формуле: (v=sqrt{{v_0}^2-2gh}).
Максимальная высота подъема тела пропорциональна квадрату начальной скорости: (H=frac{{v_0}^2}{2g}).
Формула высота подъема тела за некоторое время при известной конечной скорости: (h=frac{v+v_0}2t.)
Свободно падающее тело может двигаться прямолинейно или по криволинейной траектории. Это зависит от начальных условий. Рассмотрим это подробнее.
Свободное падение без начальной скорости: ((υ_0 = 0)). При выбранной системе координат движение тела описывается уравнениями: (υ_y=gt, y =frac{gt^2}2.) Из последней формулы можно найти время падения тела с высоты h: (t = sqrt{frac{2h}g} .) Подставляя найденное время в формулу для скорости, получим модуль скорости тела в момент падения: (υ= sqrt{2gh}.)
Если тело подбросить, то оно сначала движется равнозамедленно вверх, достигает максимальной высоты, а затем движется равноускоренно вниз. Учитывая, что при (y = h_{max}) скорость (υ_y = 0) и в момент достижения телом первоначального положения (y = 0), можно найти
(t_1=υ_0cdot g ) – время подъема тела на максимальную высоту;
(h_{max}) – максимальная высота подъема тела;
(t_2=2t_1=frac{2υ_0}g ) – время полета тела;
(v_{2y}=-v_0) – проекция скорости в момент достижения телом первоначального положения.
