Как найти расстояние между двумя точками?
Расстоянием между точками также называют прямую,
у которой одна из точек это начало, а соответственно
другая конец. Найти расстояние между этими
двумя точками, значит найти длину прямой,
связывающей точки.
Есть много разных способов найти расстояние между
двумя точками, но самый универсальный, на мой взгляд,
это найти расстояние взяв за основу Теорему Пифагора.
Исходя из этой теоремы, можно сказать, что в нашем
случае расстоянием(прямой), является гипотенуза,
а чем тогда являются точки, сейчас разберемся.
Формулировка великой Теоремы Пифагора звучит так:
в прямоугольном треугольнике квадрат гипотенузы равен
сумме квадратов катетов. Или же кратко, формулой:
( c^2 = a^2 + b^2 ) где c — это гипотенуза, a и b — катеты.
Формулировка этой теоремы применяется почти всегда и везде,
где нужно найти расстояние от чего-то до чего-то. Сейчас, мы
используя эту теорему найдем расстояние между точками.
Итак, для примера возьмем точки с координатами
первой точки — x1 = 0; y1 = 4, второй точки — x2 =3; y2 = 0.
Как же нам теперь выразить точки через катеты a и b ?
Читайте дальше, все гениальное просто.
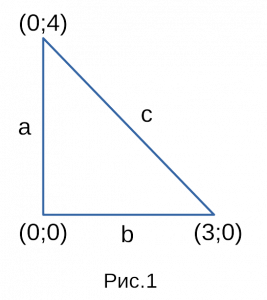
На рисунке 1 мы изобразили для наглядности
прямоугольный треугольник, с координатами
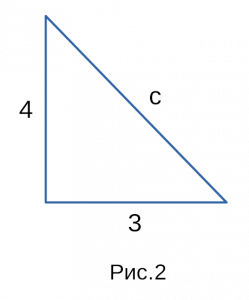
которые мы взяли для примера. На рисунке 2
тот же самый прямоугольный треугольник,
только без координат! Эти два прямоугольных
треугольника идентичные, поэтому вернемся
к Теореме Пифагора.
Заменяем длины катетов a и b, из Теоремы Пифагора,
на разность координат точек. Взгляните на формулу,
которая получилась:
Подставляем наши координаты:
В итоге получилось, что расстояние в нашем примере
равно 5(корень из 25). Как видите все просто, и вы можете
смело применять эту формулу, решая не только задачи,
но и на практике, находя расстояние зная только две точки.
Все формулы для треугольника
1. Как найти неизвестную сторону треугольника
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a , b , c – стороны произвольного треугольника
α , β , γ – противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), ( a ):
* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), ( a):
2. Как узнать сторону прямоугольного треугольника
Есть следующие формулы для определения катета или гипотенузы
a , b – катеты
c – гипотенуза
α , β – острые углы
Формулы для катета, ( a ):
Формулы для катета, ( b ):
Формулы для гипотенузы, ( c ):
Формулы сторон по теореме Пифагора, ( a , b ):
3. Формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы
b – сторона (основание)
a – равные стороны
α – углы при основании
β – угол образованный равными сторонами
Формулы длины стороны (основания), (b ):
Формулы длины равных сторон , (a):
4. Найти длину высоты треугольника
Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.
H – высота треугольника
a – сторона, основание
b, c – стороны
β , γ – углы при основании
p – полупериметр, p=(a+b+c)/2
R – радиус описанной окружности
S – площадь треугольника
Формула длины высоты через стороны, ( H ):
Формула длины высоты через сторону и угол, ( H ):
Формула длины высоты через сторону и площадь, ( H ):
Формула длины высоты через стороны и радиус, ( H ):
Расстояние от точки до прямой
Что называется расстоянием от точки до прямой? Как найти расстояние от точки до прямой?
Расстоянием от точки до прямой называется длина перпендикуляра, опущенного из данной точки на прямую.
Таким образом, чтобы найти расстояние от точки до прямой, надо из точки к прямой провести перпендикуляр и найти его длину.
Например, на рисунке 1 расстояние от точки A до прямой a равно длине перпендикуляра AB, опущенного из точки A на прямую a.
Задачи на нахождение расстояния от точки до прямой сводятся к рассмотрению прямоугольного треугольника.
№ 1. Из точки к прямой проведены две наклонные, длины которых относятся как 2:3, а длины их проекций соответственно равны 2 см и 7 см. Найти расстояние от точки до прямой.
Дано: A∉a,
BC и BD — их проекции, BC=2 см, BD=7 см
1) Пусть k — коэффициент пропорциональности. Тогда AC=2k см, AD=3k см.
2) Рассмотрим треугольник ABC — прямоугольный (так как AB — перпендикуляр к прямой a по условию). По теореме Пифагора
3) Аналогично, из треугольника ABD
4) Приравниваем правые части полученных равенств и находим k:
5) Зная k, найдем AB:
№ 2. Из точки к прямой проведены две наклонные, длины которых равны 13 см и 15 см. Найти расстояние от точки до прямой, если разность проекций наклонных равна 4 см.
Дано: A∉a,
AC и AD — наклонные, AC=13 см, AD=15 см,
BC и BD — их проекции, BD-BC=4 см
1) Пусть BC=x см, тогда BD=x+4 см.
2) Рассмотрим треугольник ABC — прямоугольный (так как AB — перпендикуляр к прямой a по условию). По теореме Пифагора
3) Аналогично, из треугольника ABD
4) Приравниваем правые части полученных равенств и находим x:
5) Зная x, найдем AB:
№ 3. Найти расстояние от точки A до прямой a, если известно, что наклонная AF, длина которой равна c, образует с прямой a угол α.
Дано: A∉a,
Треугольник ABF — прямоугольный (так как AB — перпендикуляр к прямой a по условию). AB — катет, противолежащий углу ACB, AF — гипотенуза.
[spoiler title=”источники:”]
http://www-formula.ru/2011-10-09-11-08-41
[/spoiler]
Загрузить PDF
Загрузить PDF
Теорема Пифагора связывает три стороны прямоугольного треугольника одной формулой, которой пользуются до сих пор. Теорема гласит, что в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы: a2 + b2 = c2, где a и b — катеты треугольника (стороны, пересекающиеся под прямым углом), с — гипотенуза треугольника. Теорема Пифагора применима во многих случаях, например, при помощи этой теоремы легко найти расстояние между двумя точками на координатной плоскости.
-
1
Убедитесь, что данный вам треугольник является прямоугольным, так как теорема Пифагора применима только к прямоугольным треугольникам. В прямоугольных треугольниках один из трех углов всегда равен 90 градусам.
- Прямой угол в прямоугольном треугольнике обозначается значком в виде квадрата, а не в виде кривой, которая обозначает непрямые углы.
-
2
Обозначьте стороны треугольника. Катеты обозначьте как «а» и «b» (катеты — стороны, пересекающиеся под прямым углом), а гипотенузу — как «с» (гипотенуза — самая большая сторона прямоугольного треугольника, лежащая напротив прямого угла).
-
3
Определите, какую сторону треугольника требуется найти. Теорема Пифагора позволяет найти любую сторону прямоугольного треугольника (если известны две другие стороны). Определите, какую сторону (a, b, c) необходимо найти.
- Например, дана гипотенуза, равная 5, и дан катет, равный 3. В этом случае необходимо найти второй катет. Мы вернемся к этому примеру позднее.
- Если две другие стороны неизвестны, необходимо найти длину одной из неизвестных сторон, чтобы иметь возможность применить теорему Пифагора. Для этого используйте основные тригонометрические функции (если вам дано значение одного из непрямых углов).
-
4
Подставьте в формулу a2 + b2 = c2 данные вам значения (или найденные вами значения). Помните, что a и b — это катеты, а с — гипотенуза.
- В нашем примере напишите: 3² + b² = 5².
-
5
Возведите в квадрат каждую известную сторону. Или же оставьте степени — вы можете возвести числа в квадрат позже.
- В нашем примере напишите: 9 + b² = 25.
-
6
Обособьте неизвестную сторону на одной стороне уравнения. Для этого перенесите известные значения на другую сторону уравнения. Если вы находите гипотенузу, то в теореме Пифагора она уже обособлена на одной стороне уравнения (поэтому делать ничего не нужно).
- В нашем примере перенесите 9 на правую сторону уравнения, чтобы обособить неизвестное b². Вы получите b² = 16.
-
7
Извлеките квадратный корень из обеих частей уравнения. На данном этапе на одной стороне уравнения присутствует неизвестное (в квадрате), а на другой стороне — свободный член (число).
- В нашем примере b² = 16. Извлеките квадратный корень из обеих частей уравнения и получите b = 4. Таким образом, второй катет равен 4.
-
8
Используйте теорему Пифагора в повседневной жизни, так как ее можно применять в большом числе практических ситуаций. Для этого научитесь распознавать прямоугольные треугольники в повседневной жизни — в любой ситуации, в которой два предмета (или линии) пересекаются под прямым углом, а третий предмет (или линия) соединяет (по диагонали) верхушки двух первых предметов (или линий), вы можете использовать теорему Пифагора, чтобы найти неизвестную сторону (если две другие стороны известны).
- Пример: дана лестница, прислоненная к зданию. Нижняя часть лестницы находится в 5 метрах от основания стены. Верхняя часть лестницы находится в 20 метрах от земли (вверх по стене). Какова длина лестницы?
- «в 5 метрах от основания стены» означает, что а = 5; «находится в 20 метрах от земли» означает, что b = 20 (то есть вам даны два катета прямоугольного треугольника, так как стена здания и поверхность Земли пересекаются под прямым углом). Длина лестницы есть длина гипотенузы, которая неизвестна.
- a² + b² = c²
- (5)² + (20)² = c²
- 25 + 400 = c²
- 425 = c²
- с = √425
- с = 20,6. Таким образом, приблизительная длина лестницы равна 20,6 метров.
- «в 5 метрах от основания стены» означает, что а = 5; «находится в 20 метрах от земли» означает, что b = 20 (то есть вам даны два катета прямоугольного треугольника, так как стена здания и поверхность Земли пересекаются под прямым углом). Длина лестницы есть длина гипотенузы, которая неизвестна.
Реклама
- Пример: дана лестница, прислоненная к зданию. Нижняя часть лестницы находится в 5 метрах от основания стены. Верхняя часть лестницы находится в 20 метрах от земли (вверх по стене). Какова длина лестницы?
-
1
Выберите две точки на координатной плоскости. По теореме Пифагора можно вычислить длину отрезка, соединяющего две точки на координатной прямой. Для этого необходимо знать координаты (х,у) каждой точки.
- Чтобы найти расстояние между двумя точками, вы будете рассматривать точки в качестве вершин треугольника, не прилежащих к прямому углу прямоугольного треугольника. Таким образом, вы сможете легко найти катеты треугольника, а затем вычислить гипотенузу, которая равна расстоянию между двумя точками.
-
2
Нанесите точки на координатную плоскость. Отложите координаты (х,у), где координата «х» откладывается по горизонтальной оси, а «у» — по вертикальной. Вы можете найти расстояние между точками без построения графика, но график позволяет визуально представить процесс ваших вычислений.
-
3
Найдите катеты треугольника. Вы можете сделать это, измерив длину катетов непосредственно на графике или с помощью формул: |x1 – x2| для вычисления длины горизонтального катета, и |y1 – y2| для вычисления длины вертикального катета, где (x1,y1) – координаты первой точки, а (x2,y2) – координаты второй точки.
- Пример: даны точки: А(6,1) и В(3,5). Длина горизонтального катета:
- |x1 – x2|
- |3 – 6|
- | -3 | = 3
- Длины вертикального катета:
- |y1 – y2|
- |1 – 5|
- | -4 | = 4
- Таким образом, в прямоугольном треугольнике а = 3 и b = 4.
- Пример: даны точки: А(6,1) и В(3,5). Длина горизонтального катета:
-
4
Используйте теорему Пифагора для нахождения гипотенузы. Расстояние между двумя точками равно гипотенузе треугольника, две стороны которого вы только что нашли. Используйте теорему Пифагора, чтобы найти гипотенузу, подставив в формулу найденные значения катетов (a и b).
- В нашем примере а = 3 и b = 4. Гипотенуза вычисляется следующим образом:
-
- (3)²+(4)²= c²
- c= √(9+16)
- c= √(25)
- c= 5. Расстояние между точками А(6,1) и В(3,5) равно 5.
-
Реклама
- В нашем примере а = 3 и b = 4. Гипотенуза вычисляется следующим образом:
Советы
- Гипотенуза всегда:
- лежит напротив прямого угла;
- является самой длинной стороной прямоугольного треугольника;
- обозначается как «с» в теореме Пифагора;
- √(х) означает «квадратный корень из х».
- Не забывайте проверять ответ. Если ответ кажется неправильным, проделайте вычисления снова.
- Еще один момент — самая длинная сторона лежит напротив наибольшего угла, а самая короткая сторона — напротив наименьшего угла.
- Выучите числа пифагоровой тройки, образующие стороны прямоугольного треугольника. Самая примитивная пифагорова тройка — это 3, 4, 5. Так, зная длину двух сторон, третью искать не придется.
- Помните, гипотенуза — всегда самая длинная сторона.
- Если дан обычный треугольник (а не прямоугольный), то требуется больше информации, чем просто длины двух сторон.
- Графики являются наглядным способом нанесения обозначений а, b и с. Если вы решаете задачу, то в первую очередь постройте график.
- Если дана длина только одной стороны, то теорему Пифагора применять нельзя. Попробуйте использовать тригонометрию (sin, cos, tan).
- Если речь идет о задаче из некого сюжета, можно смело предположить, что деревья, столбы, стены и так далее образуют прямой угол с землей, если не указано иное.
Реклама
Об этой статье
Эту страницу просматривали 139 979 раз.
Была ли эта статья полезной?
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a, b, c – стороны произвольного треугольника
α, β, γ – противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), (a):
* Внимательно, при подстановке в формулу, для тупого угла (α>90), cosα принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), (a):
Есть следующие формулы для определения катета или гипотенузы
a, b – катеты
c – гипотенуза
α, β – острые углы
Формулы для катета, (a):
Формулы для катета, (b):
Формулы для гипотенузы, (c):
Формулы сторон по теореме Пифагора, (a,b):
Вычислить длину неизвестной стороны через любые стороны и углы

b – сторона (основание)
a – равные стороны
α – углы при основании
β – угол образованный равными сторонами
Формулы длины стороны (основания), (b):
Формулы длины равных сторон , (a):
Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.

a – сторона, основание
b, c – стороны
β, γ – углы при основании
p – полупериметр, p=(a+b+c)/2
R – радиус описанной окружности
S – площадь треугольника
Формула длины высоты через стороны, (H):
Формула длины высоты через сторону и угол, (H):
Формула длины высоты через сторону и площадь, (H):
Формула длины высоты через стороны и радиус, (H):
В прямоугольном треугольнике катеты, являются высотами. Ортоцентр – точка пересечения высот, совпадает с вершиной прямого угла.
H – высота из прямого угла
a, b – катеты
с – гипотенуза
c1 , c2 – отрезки полученные от деления гипотенузы, высотой
α, β – углы при гипотенузе
Формула длины высоты через стороны, (H):
Формула длины высоты через гипотенузу и острые углы, (H):
Формула длины высоты через катет и угол, (H):
Формула длины высоты через составные отрезки гипотенузы , (H):
L– биссектриса, отрезок |OB|, который делит угол ABC пополам
a, b – стороны треугольника
с – сторона на которую опущена биссектриса
d, e – отрезки полученные делением биссектрисы
γ – угол ABC , разделенный биссектрисой пополам
p – полупериметр, p=(a+b+c)/2
Длина биссектрисы через две стороны и угол, (L):
Длина биссектрисы через полупериметр и стороны, (L):
Длина биссектрисы через три стороны, (L):
Длина биссектрисы через стороны и отрезки d, e, (L):
Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.
1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:
L – биссектриса, отрезок ME , исходящий из прямого угла (90 град)
a, b – катеты прямоугольного треугольника
с – гипотенуза
α – угол прилежащий к гипотенузе
Формула длины биссектрисы через катеты, ( L):
Формула длины биссектрисы через гипотенузу и угол, ( L):
2. Найти по формулам длину биссектрисы из острого угла на катет:
L – биссектриса, отрезок ME , исходящий из острого угла
a, b – катеты прямоугольного треугольника
с – гипотенуза
α, β – углы прилежащие к гипотенузе
Формулы длины биссектрисы через катет и угол, (L):
Формула длины биссектрисы через катет и гипотенузу, (L):
L – высота = биссектриса = медиана
a – одинаковые стороны треугольника
b – основание
α – равные углы при основании
β – угол образованный равными сторонами
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
Формула высоты, биссектрисы и медианы, через стороны, (L):
Формула для вычисления высоты = биссектрисы = медианы.
В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.
L – высота=биссектриса=медиана
a – сторона треугольника
Формула длины высоты, биссектрисы и медианы равностороннего треугольника, (L):
Медиана – отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.
Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.
M – медиана, отрезок |AO|
c – сторона на которую ложится медиана
a, b – стороны треугольника
γ – угол CAB
Формула длины медианы через три стороны, (M):
Формула длины медианы через две стороны и угол между ними, (M):
Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c, пополам.
Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности (R).

M – медиана
R – радиус описанной окружности
O – центр описанной окружности
с – гипотенуза
a, b – катеты
α – острый угол CAB
Медиана равна радиусу и половине гипотенузы, (M):
Формула длины через катеты, (M):
Формула длины через катет и острый угол, (M):
Калькулятор длин сторон треугольника онлайн умеет вычислять длину сторон 14 способами.
Калькулятор может:
- Найти все стороны треугольника.
- Найти все углы треугольника.
- Найти площадь (S) и периметр (P) треугольника.
- Найти радиус (r) вписанной окружности.
- Найти радиус (R) описанной окружности.
- Найти высоту (h) треугольника.
Просто введите любые имеюшиеся данные и, если их достаточно, то калькулятор сам подберет нужные формулы для вычислений и покажет подробный расчет с выводом формул.
Сторона треугольника (или длина сторон) может быть найдена различными методами.
В большинстве случаев достаточно воспользоваться одной из ниже приведенных формул. Однако не редки случаи когда для нахождения искомой стороны понадобиться обратиться к дополнительным материалам или решения в два действия.
Как найти длину стороны треугольника?
Найти длину сторон треугольника очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.
Для прямоугольного треугольника:
1) Найти катет через гипотенузу и другой катет
где a и b – катеты, с – гипотенуза.
2) Найти гипотенузу по двум катетам
где a и b – катеты, с – гипотенуза.
3) Найти катет по гипотенузе и противолежащему углу
где a и b – катеты, с – гипотенуза,α° и β° – углы напротив катетов.
4) Найти гипотенузу через катет и противолежащий угол
где a и b – катеты, с – гипотенуза,α° и β°- углы напротив катетов.
Для равнобедренного треугольника:
1) Найти основание через боковые стороны и угол между ними
где a – искомое основание, b – известная боковая сторона,α° – угол между боковыми сторонами.
2) Найти основание через боковые стороны и угол при основании
где a – искомое основание,b – известная боковая сторона,β° – угол при осноавнии.
3) Найти боковые стороны по углу между ними
где b – искомая боковая сторона, a – основание,α° – угол между боковыми сторонами.
4) Найти боковые стороны по углу при основании
где b – искомая боковая сторона, a – основание,β° – угол при осноавнии.
Для равностороннего треугольника:
1) Найти сторону через площадь
где a – искомая сторона, S – площадь треугольника.
2) Найти сторону через высоту
где a – искомая сторона,h – высота треугольника.
3) Найти сторону через радиус вписанной окружности
где a – искомая сторона,r – радиус вписанной окружности.
4) Найти сторону через радиус описанной окружности
где a – искомая сторона,R – радиус описанной окружности.
Для произвольного треугольника:
1) Найти сторону через две известные стороны и один угол (теорема косинусов)
где a – искомая сторона, b и с – известные стороны, α° – угол напротив неизвестной стороны.
2) Найти сторону через одну известную сторону и два угла (теорема синусов)
где a – искомая сторона, b – известная сторона, α° и β° известные углы.
Скачать все формулы в формате Word
Расстояния
Задача на нахождения расстояния в стереометрической фигуре является главной и самой важной из всех. Прежде всего определимся с тем, что имеется ввиду под словом «расстояние», ведь их может быть бесконечно много.
Расстояние между объектами в геометрии – это кратчайшее из расстояний между ними.
Обозначение:
В стереометрии найти расстояние можно между следующими комбинациями фигур:
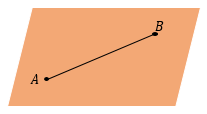
РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ
Расстояние между точками– это длина отрезка, соединяющего эти точки.
В задачах на стереометрию мы не можем просто воспользоваться линейкой, и длину этого отрезка должны найти аналитически. Поэтому длину отрезка AB между точками A и B находят как сторону треугольника, если отрезок AB удается включить в некоторый треугольник в качестве одной из его сторон.
То есть если в задаче предлагается найти расстояние между точками, нужно задать себе вопрос: «В каком треугольнике этот отрезок является стороной?», затем построить этот треугольник и найти в нем нужную сторону.
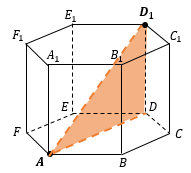
Например:
|
|
|
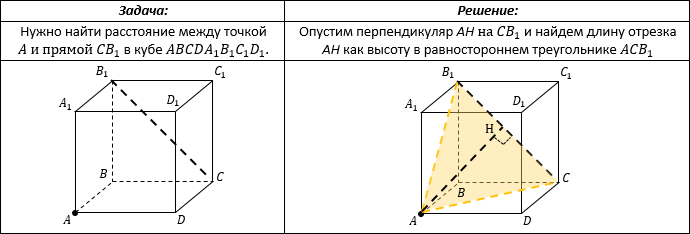
РАССТОЯНИЕ МЕЖДУ ТОЧКОЙ И ПРЯМОЙ
Расстояние от точки до прямой – длина перпендикуляра, опущенного из точки на прямую.
Этот отрезок перпендикуляра можно вычислить, включив его в треугольник (или трапецию) в качестве одной из высот. То есть нужно задать себе вопрос: «В каком треугольнике этот отрезок является высотой?», затем построить этот треугольник и найти в нем высоту.
Например:
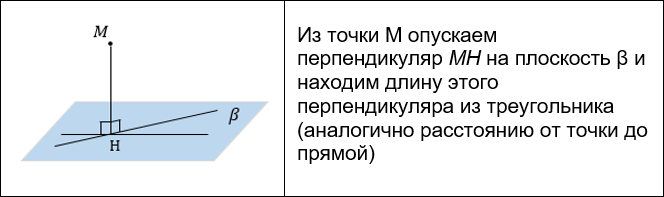
РАССТОЯНИЕ МЕЖДУ ТОЧКОЙ И ПЛОСКОСТЬЮ
Существует несколько способов нахождения расстояния от точки до плоскости:
- Построение перпендикуляра из точки на плоскость.
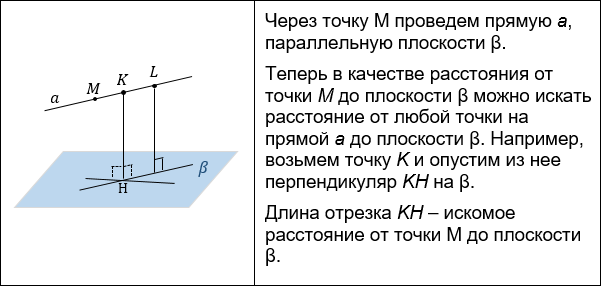
- К этому способу обращаются, если расстояние из точки M на плоскость опускать неудобно, а удобно опустить равный ему перпендикуляр из другой точки, лежащей на одной линии с M.
- Построение перпендикуляра из точки прямой к плоскости.
- Построение перпендикуляра из точки плоскости на плоскость.
К этому способу, аналогично, обращаются, если расстояние из точки M на плоскость опускать неудобно, а удобно опустить равный ему перпендикуляр из другой точки, лежащей на одной плоскости с M.
- Через двойное выражение объема.
Расстояние от точки M до плоскости β – это перпендикуляр, опущенный из точки на плоскость, то есть по сути это высота в некоторой пирамиде с вершиной M и плоскостью основания, лежащей на β. Если легко вычислить объем этой пирамиды, используя другое основание и другую высоту, то через этот объем можно найти нужное расстояние.
Например:
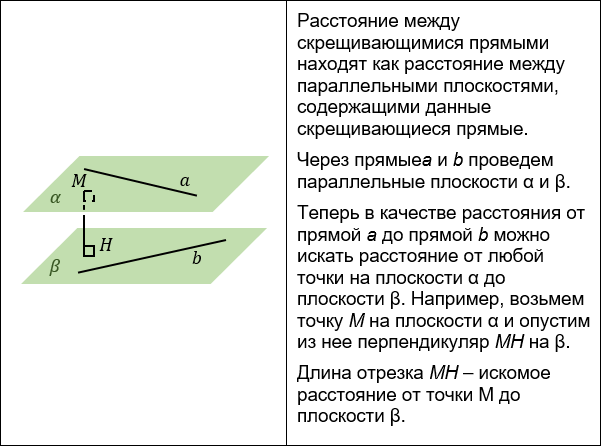
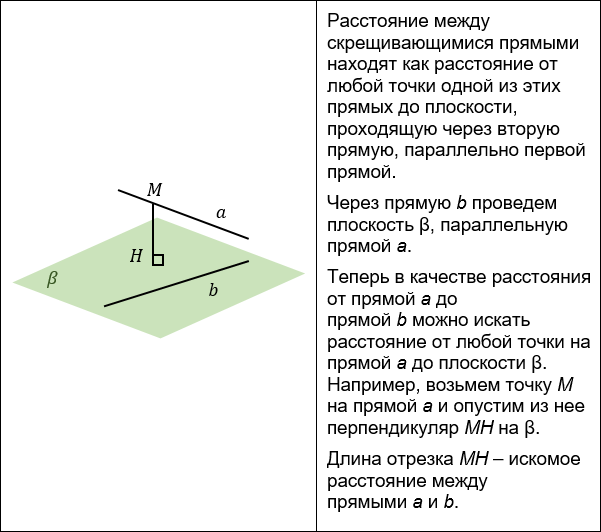
РАССТОЯНИЕ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ
Существует несколько способов нахождения расстояния между скрещивающимися прямыми:
1. Построение взаимного перпендикуляра.
2. Построение параллельной прямой.
К этому способу обращаются, если строить взаимный перпендикуляр неудобно и одна из скрещивающихся прямых уже заключена в удобную плоскость.
3. Построение параллельной плоскости.