В этом учебном материале по Excel мы рассмотрим примеры того, как рассчитать расстояние между двумя точками на координатной плоскости.

Основная формула
|
=КОРЕНЬ((x2–x1)^2+(y2–y1)^2) |
Описание
Чтобы вычислить длину отрезка по координатам двух точек на линии, вы можете использовать формулу расстояния, адаптированную для синтаксиса формул Excel. В показанном примере формула в G5, имеет следующий вид:
|
=КОРЕНЬ((D5–B5)^2+(E5–C5)^2) |
где координаты двух точек указаны в столбцах с B по E.
Пояснение
Длину линии можно рассчитать по формуле расстояния, которая выглядит так:
Расстояние – это квадратный корень из изменения x в квадрате плюс изменение y в квадрате, где две точки даны в форме (x1, y1) и (x2, y2).
Формула расстояния – это пример примененной теоремы Пифагора, где изменение x и изменение y соответствуют двум сторонам прямоугольного треугольника, а гипотенуза – вычисляемому расстоянию.
В Excel формулу расстояния можно записать с помощью оператора экспоненты ^ и функции КОРЕНЬ следующим образом:
|
=КОРЕНЬ((D5–B5)^2+(E5–C5)^2) |
В соответствии с порядком операций Excel, изменение x и изменение y вычисляется, затем возводится в квадрат, и два результата складываются вместе и передаются в функцию КОРЕНЬ, которая возвращает квадратный корень из суммы в качестве окончательного результата:
|
=КОРЕНЬ((D5–B5)^2+(E5–C5)^2) =КОРЕНЬ((6)^2+(8)^2) =КОРЕНЬ(36+64) =КОРЕНЬ(100) =10 |
Функцию СТЕПЕНЬ также можно использовать вместо оператора экспоненты ^ следующим образом:
|
=КОРЕНЬ(СТЕПЕНЬ(D5–B5;2)+СТЕПЕНЬ(E5–C5;2)) |
с тем же результатом.
You might think “as the crow flies” distance is nothing more than a simple hypotenuse calculation back from geometry class. Unfortunately, not. You should work with either decimal degrees or degree-minute-second (DMS) notation due to the curvy structure of Earth. This means a lot of formulas to deal with.
Also, you need coordinates (latitude/longitude) of each city you want to put in a calculation.
Thankfully, we have workarounds for both problems. In this article, we are going to show how to calculate as-the-crow-flies distance between two cities in Excel with help of LAMBDA function and data types.
Download Workbook
The formula of calculating distance by longitude and latitude
In our example, we are using the great-circle distance method which uses the shortest path, also known as, as the crow flies, between two points corresponding to an arc linking two points on a sphere. The method uses Spherical law of cosines a theorem relating the sides and angles of spherical triangles.
![]()
where
- φ: Latitude (radian)
- λ: Longitude (radian)
- R: Radius of the earth
The coordinates are represented in two forms:
- As a string including degree, minute and second
- As a numerical value of decimal degrees
Converting degrees, minutes and seconds to decimal degrees:
Decimal Degrees = Degrees + (Minutes + Seconds / 60) / 60
Converting decimal degrees to radians:
Radians = Decimal Degrees * PI / 180
Because deg-min-sec notation will make things more confusing, we will use decimal degrees going forward. This is the Excel formula for decimal degrees:
ACOS( SIN(Place1_Lat * PI() / 180) * SIN(Place2_Lat * PI() / 180) + COS(Place1_Lat * PI() / 180) * COS(Place2_Lat * PI() / 180) * COS(Place2_Lon * PI() / 180 - Place1_Lon * PI() / 180) ) * EarthRadius
Obviously, no one wants to deal with this kind of formula more than one time. Instead, you can use the LAMBDA function to define this formula once in a named range and use the named range like a UDF (user-defined function). Let’s see what the LAMBDA function is and how you can use it.
LAMBDA Function
The LAMBDA function is a game changer feature that allows you to create your own functions without any VBA, macro, or JavaScript knowledge. Since its unique nature, the function has a unique use case.
- A LAMBDA formula should be written in a named range. That named range’s name will be your custom function’s name.
- You need to type parameter names before the function itself. Such as, a and b are the parameters and the latter operation is the function itself: =LAMBDA(a, b, a-b)
- LAMBDA functions can be called recursively.
LAMBDA([parameter1, parameter2, …,] calculation)
For detailed information, please visit the following page: Excel LAMBDA Function
The LAMBDA function requires a Microsoft 365 subscription.
Calculating distance by longitude and latitude with LAMBDA Function
Let’s create our custom function as described above. The distance formula needs 4 arguments, if we use a static value for the radius of earth, e.g., 6,371 km.
=LAMBDA(Place1_Lat, Place1_Lon, Place2_Lat, Place2_Lon,
ACOS(
SIN(Place1_Lat * PI() / 180) * SIN(Place2_Lat * PI() / 180) +
COS(Place1_Lat * PI() / 180) * COS(Place2_Lat * PI() / 180) *
COS(Place2_Lon * PI() / 180 - Place1_Lon * PI() / 180)
) * 6371
)

Once created, you can re-use your custom function anywhere in this workbook. Excel even displays IntelliSense box for this function.

Tip: You can use Excel’s RADIANS function instead of multiplying by PI() / 180.
=LAMBDA(Place1_Lat,Place1_Lon,Place2_Lat,Place2_Lon,ACOS(SIN(RADIANS(Place1_Lat))*SIN(RADIANS(Place2_Lat))+COS(RADIANS(Place1_Lat))*COS(RADIANS(Place2_Lat))*COS(RADIANS(Place2_Lon)-RADIANS(Place1_Lon)))*6371)
Data Types
Let us introduce you to an Excel feature called “Data Types”. The Data Types feature allows pulling data dynamically from online sources. Geographical data like countries and cities are two of them. This feature will relieve you from gathering coordinate data beforehand.
Note: Data Types have been released to all Microsoft 365 subscribers on March 28, 2019. Thus, you need to be a Microsoft 365 subscriber to access this feature.
You can find the feature button under the Data tab of the Ribbon.
All you need to do is to select cells that contain a city name and click the Geography icon. You will see an icon will be added to city names.

Once added, you can see options like population, time zone, and more, including latitude and longitude by putting a dot (.) after the cell’s reference.

Since you can get lat/lon values from a single data-type cell why do you need four arguments in your custom function? You can simplify decrease your argument number to two like below:
=LAMBDA(City1, City2,
ACOS(
SIN(City1.Latitude * PI() / 180) *
SIN(City2.Latitude * PI() / 180) +
COS(City1.Latitude * PI() / 180) *
COS(City2.Latitude * PI() / 180) *
COS(
City1.Longitude * PI() / 180 -
City2.Longitude * PI() / 180
)
) * 6371
)
We named our formula “DistanceByCity”:

Здравствуйте!
Пытаюсь постичь парсинг сайтов посредством VBA с выводом данных в Excel.
Очень нужная фича от
Андрей_26
, но я так же как и ТС не смог разобраться: почему у меня код не работает и как это лечить! И есть простое человеческое желание не пользоваться [потенциально] платными ресурсами гугла, яндекса и прочих. Соответственно ресурс
https://issa.ru/distance/
рулит пока – не реклама, тем более что есть негативные о ресурсе отзывы – issa не всегда срабатывает с первого раза.
То что понял(?) и вопросы написал подробно в комментариях по каждой строке кода, чтобы и идущим за мной была ясность:
| Код |
|---|
Sub Rasstoyanie()
Application.ScreenUpdating = False 'отключаем обновление экрана
Dim IE As Object, t$ 'объявляем переменные VBA
Set IE = CreateObject("InternetExplorer.Application") 'запуск мелкософтского браузера
IE.Visible = 1 '1 (или True) - отображаем браузер; 0 (или False)- не отображаем браузер _
'- MS IE работает инкогнито!
S = "https://issa.ru/distance/" 'адрес веб-страницы
IE.Navigate (S) 'браузер обращается к указанной веб-странице
Do While IE.Busy Or (IE.readyState <> 4): DoEvents: Loop 'не вникал, но предполагаю это _
'ожидание открытия веб-страницы
IE.Document.getelementbyid("gui-input-source").Value = Range("A2").Value 'gui-input-source _
'- значение переменной "начало пути" для веб-страницы берем из A2 Excel'я
IE.Document.getelementbyid("gui-input-target").Value = Range("B2").Value 'gui-input-target _
'- значение переменной "конец пути" для веб-страницы берем из B2 Excel'я
IE.Document.getelementbyid("gui-calculate").Click 'эмулируем нажатие на веб-странице кнопки _
'"Рассчитать[расстояние]"
Application.Wait (Now() + TimeValue("00:00:08")) 'приложение Excel ожидает 8 секунд для _
'обработки данных, построения маршрута и расчетов на веб-странице
t = IE.Document.body.innerHtml 'собственно весь код веб-страницы - ???
Dim REGEXP As Object 'объявляем новый объект
Set REGEXP = CreateObject("VBScript.RegExp") 'Создание объекта регулярных выражений - это и _
'нижеследующее читал на http://script-coding.com/WSH/RegExp.html
REGEXP.IgnoreCase = True
REGEXP.Global = False
REGEXP.MultiLine = True
REGEXP.Pattern = "d[^s]* <span>км" '<=== А ВОТ ТУТ ВООБЩЕ НЕ ПОНЯЛ!!! .Pattern - строка, _
'используемая как шаблон. НО! В коде элементов веб-страницы не нашел такой конструкции! _
'Что такое "d[^s]*"? Либо не понял конструкцию, либо на сайте были изменения с момента _
'опубликования поста
If REGEXP.test(t) Then
Range("C2").Value = Replace(REGEXP.Execute(t)(0), "d[^s]* <span>км", "") ' - ???
End If
IE.Quit 'закрываем браузер
Application.ScreenUpdating = True 'включаем обновление экрана
MsgBox "Готово!"
End Sub
|
Убрал цикл по строкам в Excel’е – поиск расстояния между адресами происходит по одной строке: старт – финиш; интересует только расстояние между адресами, не время в пути и расход топлива.
Собственно вопрос: либо в коде элементов веб-страницы сейчас нет конструкции “d[^s]*<span>км” (см.скрин), либо вообще не понял конструкцию.
ps WIN 10 PRO x64, Excel 2010 x32, VBA 7.0
17 авг. 2022 г.
читать 1 мин
Евклидово расстояние между двумя векторами, A и B, рассчитывается как:
Евклидово расстояние = √ Σ(A i -B i ) 2
куда:
- Σ — греческий символ, означающий «сумма».
- A i — i -е значение в векторе A
- B i — i -е значение в векторе B
Чтобы вычислить евклидово расстояние между двумя векторами в Excel, мы можем использовать следующую функцию:
= SQRT ( SUMXMY2 (RANGE1, RANGE2))
Вот что делает формула в двух словах:
- SUMXMY2 находит сумму квадратов разностей соответствующих элементов диапазона 1 и диапазона 2.
- SQRT извлекает квадратный корень из этой суммы квадратов разностей.
Конечный результат, если евклидово расстояние между двумя диапазонами.
Например, предположим, что у нас есть следующие два вектора, A и B, в Excel:
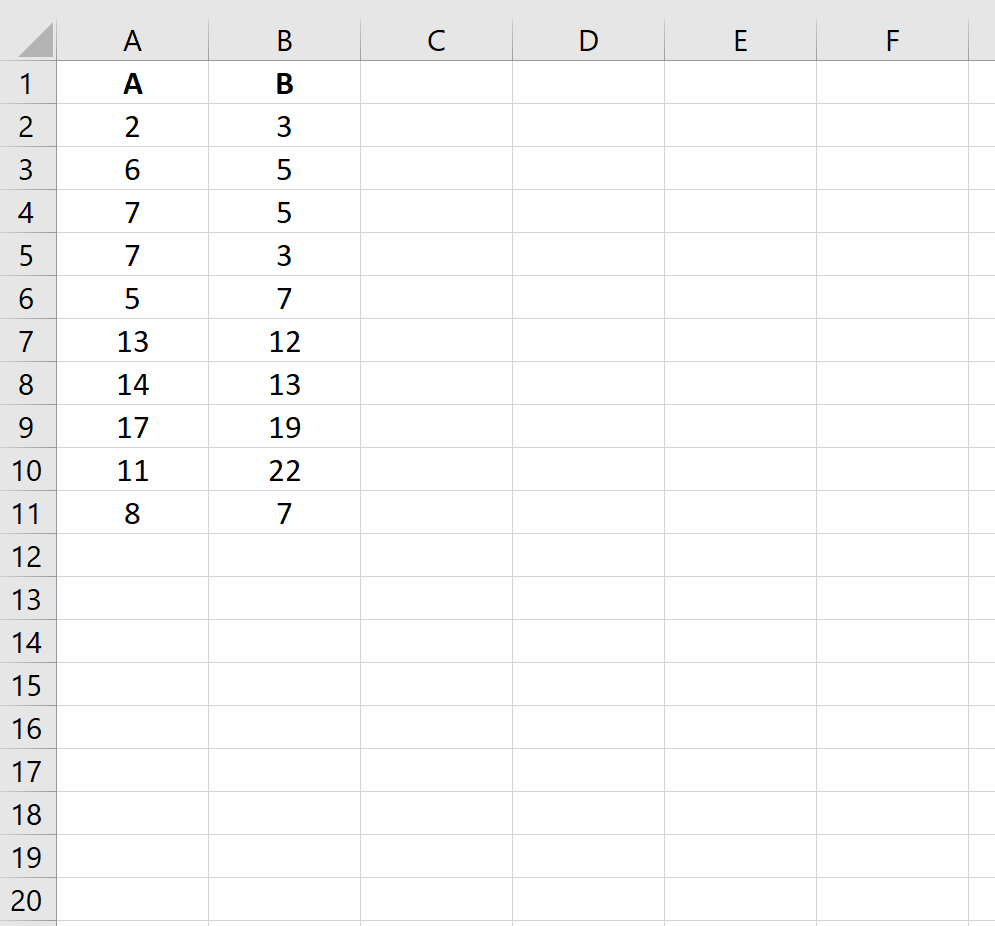
Мы можем использовать следующую функцию для вычисления евклидова расстояния между двумя векторами:
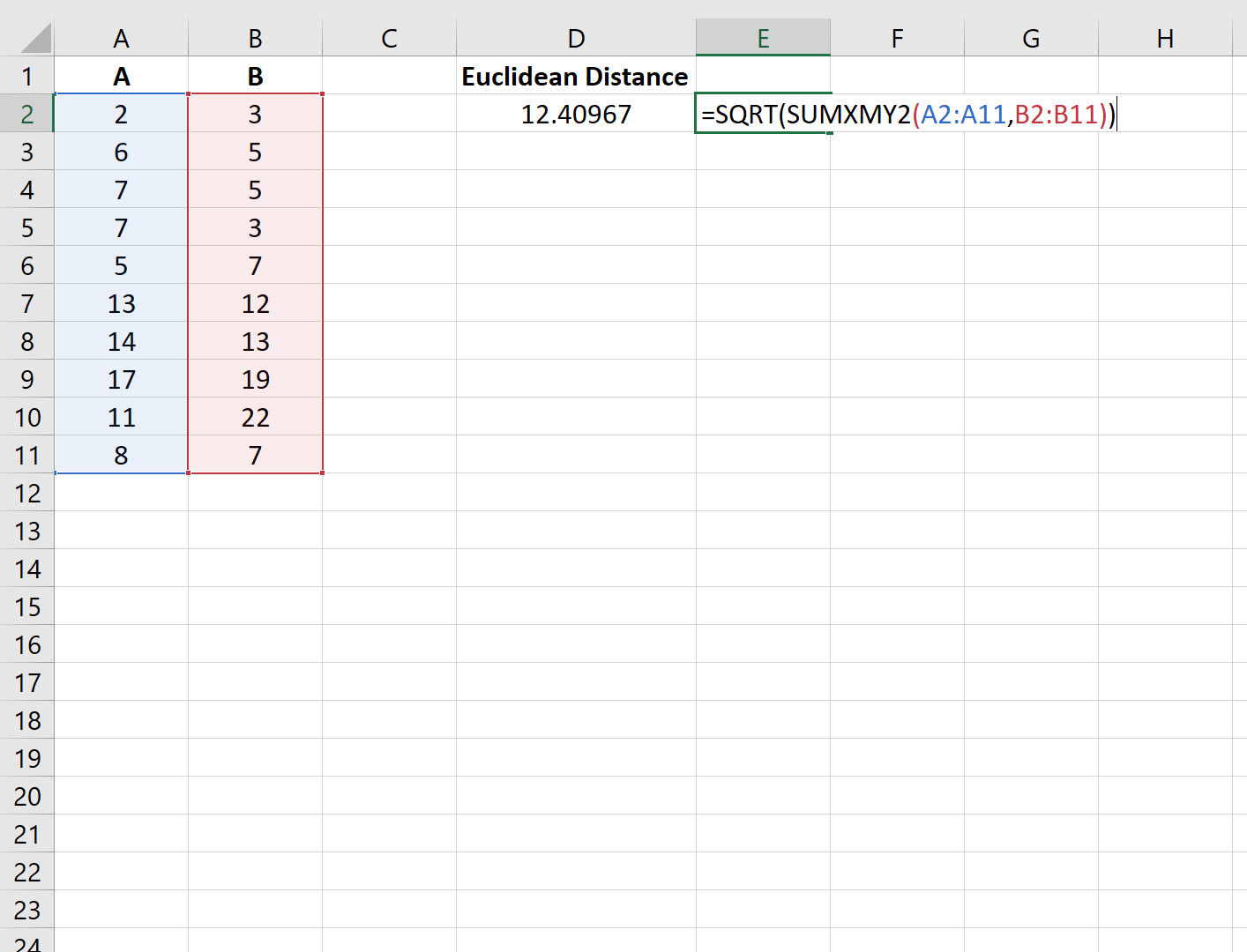
Евклидово расстояние между двумя векторами оказывается равным 12,40967 .
Обратите внимание, что эта функция будет включать только полные парные наблюдения при вычислении евклидова расстояния.
Например, последние две строки в столбце A не будут включены в расчет евклидова расстояния между следующими двумя векторами:
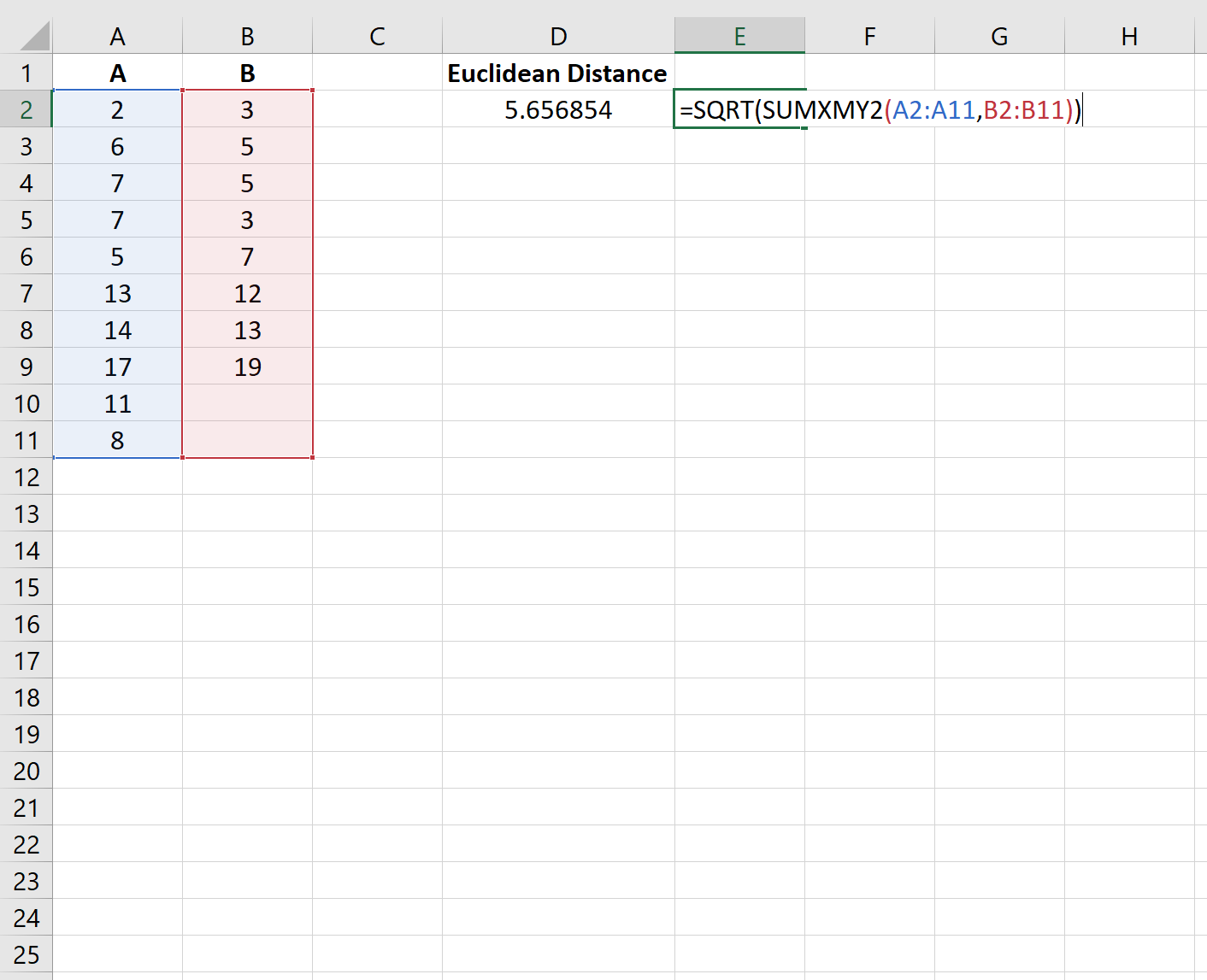
Евклидово расстояние между двумя векторами оказывается равным 5,656854 .
Дополнительные ресурсы
Как рассчитать евклидово расстояние в R
Как рассчитать евклидово расстояние в Python
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
Задача простая. Нужно вычислить расстояние между двумя точками на карте, при этом известны только их географические координаты, то есть широта и долгота. Для примера вычислим расстояние между Москвой и Питером, но данная методика, конечно же, будет применима и к другим двум точкам местности. В наше время у многих людей есть такие компасы, например при смартфонах, которые показывают не только направление, но и географические координаты.
Итак, задача: вычислить расстояние между двумя городами. Известно только одно – географические координаты, то есть широта и долгота. Посмотрим эти данные в справочнике, ну или в Википедии.
Итак, что нам известно: координаты Москвы:
55,7522 град. с.ш., 37.6156 град. в.д.
Координаты Петербурга:
59,89444 град. с.ш., 30,26417 град. в.д.
Построим с помощью Excel трапецию:
Итак, у нас есть трапеция ABCD. На ней точка D – это Москва, точка B – это Петербург. Отрезок AB проходит по меридиану Петербурга, BC – по параллели Петербурга, CD – по меридиану Москвы и AD – по параллели Москвы.
Что нам известно? Во-первых известны все географические координаты каждой из точек:
A: 55,7522, 30,26417;
B: 59,89444, 30,26417;
C: 59,89444, 37,6156;
D: 55,7522, 37,6156.
Вычислить AB и CD достаточно просто. На меридианах в градусе примерно одинаковое число километров. Это расстояние можно взять из справочных данных, и оно составляет примерно 111,1 км в каждом градусе.
Нужная нам разница в градусах – это 59,89444-55,7522, или 4,14224. А это значит, что разница в километрах – это 4,14224*111,1=460,2029 км.
Что же касается оснований трапеции, там тоже все достаточно просто. Экватор – это ноль градусов северной широты, и длина каждого градуса на экваторе около 111,3 км. Поскольку косинус ноля – это единица, то для любой параллели верна следующая формула: длина каждого градуса равна произведению 111,3 на косинус того угла, который числится в градусах северной широты (ну или южной, если это происходит южнее экватора).
Итак, с помощью Excel вычислим нужные нам косинусы:
- cos(55.7522) = 0,562773
- cos(59.89444) = 0,501595
Это значит, что 1 градус в верхнем основании нашей трапеции =111,3*0,501595=55,82749 км, а один градус в нижнем основании трапеции =111,3*0,562773=62,6366 км. Поскольку число градусов одинаково как в верхнем, так и в нижнем основаниях трапеции и составляет 37,6156-30,26417, то есть 7,35143 градуса. Но число километров в верхнем и нижнем основаниях трапеции не одинаковое.
Рассчитаем эти расстояния в километрах. BC=7,35143*55,82749=410,4119 км.
AD=7,35143*62,6366=460,469 км.
Теперь проведем высоту BH в нашей трапеции:
В прямоугольном треугольнике ABH нам известно, что гипотенуза равна 460,2029 км, малый катет тоже известен (это половина разницы между длинами оснований трапеции, то есть 0,5*[460,469-410,4119], то есть 0,5*50,05711, или 25,02856 км).
Итак, найдем высоту трапеции ABCD, ее можно вычислить с помощью теоремы Пифагора. Напомню, что мы знаем и длину гипотенузы, и длину наименьшего из катетов.
- Квадрат гипотенузы: 211786,7
- Квадрат известного катета: 626,4
- Разность между этими числами: 211160,2
Корень из этой разности – 459,5218 км. Это и есть наша высота трапеции, то есть BH.
Задача почти решена. Для нахождения расстояния между Москвой и Питером нам нужно вычислить диагональ трапеции, то есть BD. Нарисуем эту линию:
Итак, у нас есть треугольник BHD. BH мы только что вычислили (459,5218 км), HD тоже известно (нужно от большего основания трапеции отнять AH. 460,469-25,02856=435,4404).
Два катета известны, нужно найти гипотенузу. По той же теореме Пифагора, и мы увидим, что гипотенуза будет равна 633,0629 км. Это и есть расстояние от Питера до Москвы.
Проверим наши вычисления, спросив у Яндекса, сколько составляет расстояние от Питера до Москвы.
Мы увидим ответ – 634 км. При вычислениях по нашей методике получилось чуть больше, чем 633 км. Это значит, что погрешность при данном виде вычислений достаточна мала. Но если учесть, что крупные города – это не маленькие точки, а большие расстояния с севера на юг и с запада на восток, то можно сказать, что мы вычислили все правильно.
