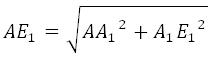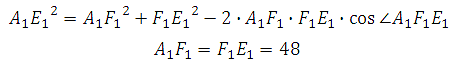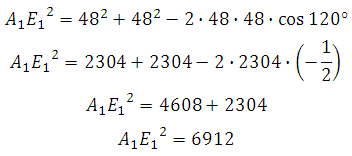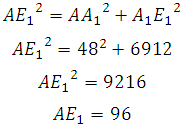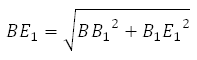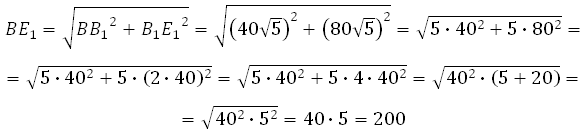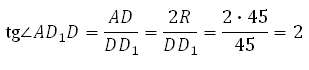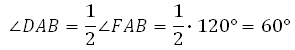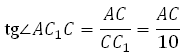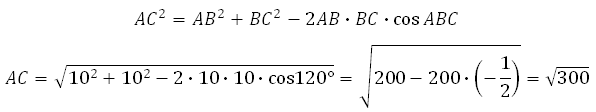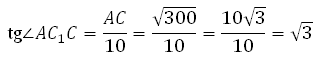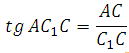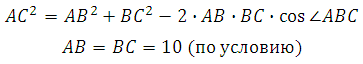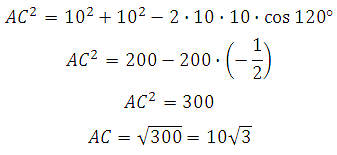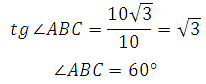Решение:
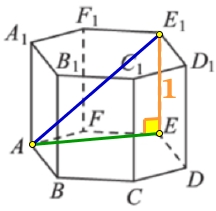
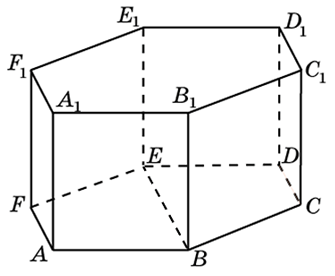
Рассмотрим прямоугольный ΔАE1E, в нём катет EE1 = 1, как ребро призмы, катет АE найдём из основания призмы – правильного шестиугольника:
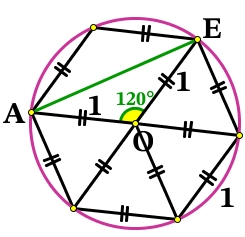
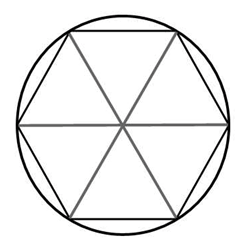
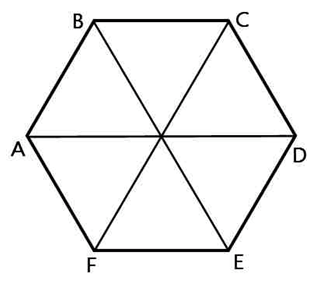
Если вокруг шестиугольника описать окружность и из её центра провести радиусы к вершинам шестиугольника, получим равносторонние треугольники со сторонами 1 и углами равными 60º.
Рассмотрим ΔАОE в нём стороны АО = ОE = 1, а ∠АОE = 60º + 60º = 120º. По теореме косинусов найдём сторону АE:
АE2 = АО2 + ОE2 – 2·АО·ОE·сos∠АОС
АE2 = 12 + 12 – 2·1·1·сos120º
АE2 = 2 – 2·(–½)
АE2 = 2 + 1
АE2 = 3
AE = √3
В прямоугольном ΔAE1E, по теореме Пифагора, найдём AE1:
AE12 = EE12 + AE2
AE12 = 12 + √32
AE12 = 1 + 3
AE12 = 4
AE1 = √4 = 2
Ответ: 2.
На сайте уже были рассмотрены некоторые типы задач по стереометрии, которые входят в единый банк заданий экзамена по математике. Например, задания про составные многогранники.
Призма называется правильной если её боковые перпендикулярны основаниям и в основаниях лежит правильный многоугольник. То есть правильная призма – это прямая призма, у которой в основании правильный многоугольник.
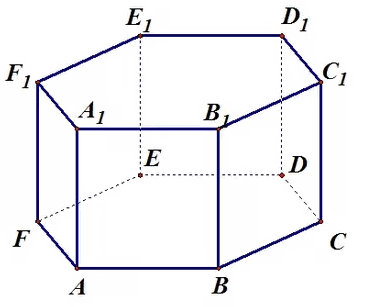
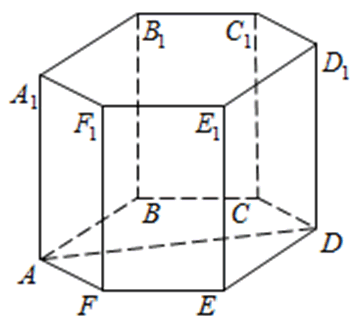
Правильная шестиугольная призма – в основании правильный шестиугольник, боковые грани – прямоугольники.
В этой статье для вас задачи на решение призмы, в основании которой лежит правильный шестиугольник. Особенностей и сложностей в решении нет никаких. В чём суть? Дана правильная шестиугольная призма, требуется вычислить расстояние между двумя вершинами или найти заданный угол. Задачи на самом деле простые, в итоге решение сводится к нахождению элемента в прямоугольном треугольнике.
Используется теорема Пифагора и теорема косинусов. Необходимо знание определений тригонометрических функций в прямоугольном треугольнике.
Обязательно посмотрите информацию о правильном шестиугольнике в этой статье (пункт 6). Ещё вам пригодится навык извлечения квадратного корня их большого числа. Можете посмотреть статью на решение многогранников, там тоже вычисляли расстояние между вершинами и углы.
Кратко: что представляет собой правильный шестиугольник?
Известно, что в правильном шестиугольнике стороны равны. Кроме этого, углы между сторонами тоже равны.
*Противолежащие стороны параллельны.
Дополнительная информация
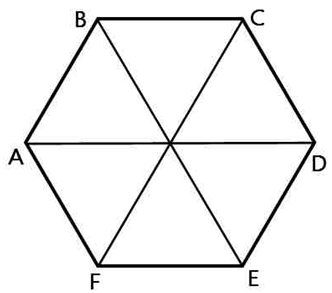
Радиус окружности описанной около правильного шестиугольника равен его стороне. *Это подтверждается очень просто: если мы соединим противоположные вершины шестиугольника, то получим шесть равных равносторонних треугольников. Почему равносторонних?
У каждого треугольника угол при его вершине лежащей в центре равен 600 (360:6=60). Так как у треугольника две стороны имеющие общую вершину в центре равны (это радиусы описанной окружности), то каждый угол при основании такого равнобедренного треугольника так же равен 60 градусам.
То есть правильный шестиугольник, образно говоря, состоит как бы из шести равных равносторонних треугольников.
Какой полезный для решения задач факт ещё следует отметить? Угол при вершине шестиугольника (угол между его соседними сторонами) равен 120 градусам.
*Умышленно не коснулись формул правильного N-угольника. Данные формулы мы подробно рассмотрим в будущем, здесь они просто не нужны.
Рассмотрим задачи:
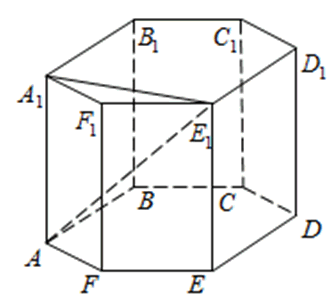
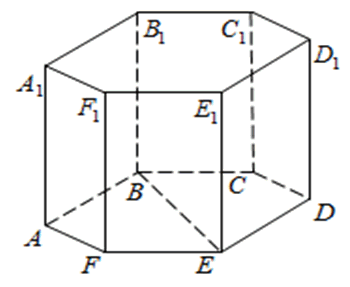
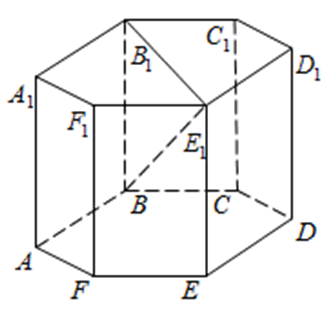
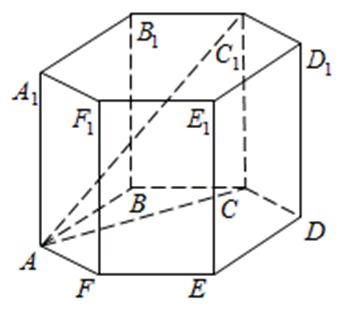
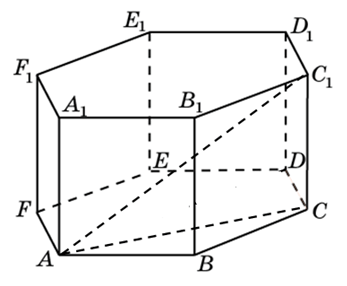
272533. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 48. Найдите расстояние между точками A и E1.
Рассмотрим прямоугольный треугольник AA1E1. По теореме Пифагора:
*Угол между сторонами правильного шестиугольника равен 120 градусам.
Отрезок АЕ1 является гипотенузой, АА1 и А1Е1 катеты. Ребро АА1 нам известно. Катет А1Е1 мы можем найти используя используя теорему косинусов.
Теорема: Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними.
Следовательно
По теореме Пифагора:
Ответ: 96
*Обратите внимание, что 48 возводить в квадрат совсем не обязательно.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 35. Найдите расстояние между точками B и E.
Рассмотрим правильный шестиугольник:
Сказано, что все рёбра равны 35, то есть сторона шестиугольника лежащего в основании равна 35. А так же, как уже сказано, радиус описанной около него окружности равен этому же числу.
Таким образом,
Ответ: 70
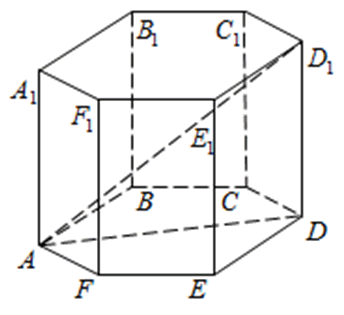
273353. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны сорока корням из пяти. Найдите расстояние между точками B и E1.
Рассмотрим прямоугольный треугольник BB1E1. По теореме Пифагора:
Отрезок B1E1 равен двум радиусам описанной около правильного шестиугольника окружности, а её радиус равен стороне шестиугольника, то есть
Таким образом,
Ответ: 200
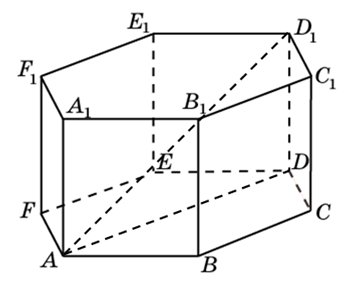
273683. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 45. Найдите тангенс угла AD1D.
Рассмотрим прямоугольный треугольник ADD1, в котором AD равно диаметру окружности, описанной вокруг основания. Известно, что радиус окружности, описанной вокруг правильного шестиугольника равен его стороне.
Таким образом,
Ответ: 2
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 23. Найдите угол DAB. Ответ дайте в градусах.
Рассмотрим правильный шестиугольник:
В нём углы между сторонами равны 120°. Значит,
Сама длина ребра не имеет значения, на величину угла она не влияет.
Ответ: 60
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 10. Найдите угол AC1C. Ответ дайте в градусах.
Рассмотрим прямоугольный треугольник AC1C:
Найдём AC. В правильном шестиугольнике углы между его сторонами равны 120 градусам, тогда по теореме косинусов для треугольника АВС :
Таким образом,
Значит, угол AC1C равен 60 градусам.
Ответ: 60
274453. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 10. Найдите угол AC1C. Ответ дайте в градусах.
Рассмотрим треугольник AС1С, он прямоугольный. Вычислим тангенс указанного в условии угла и определим угол. Известно, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему, то есть
Катет С1С = 10. Отрезок АС вычислим по теореме косинусов (это мы уже делали в первой задаче, запишем ещё раз):
В правильном шестиугольнике углы при вершинах равны 120 градусам, то есть
Следовательно
Таким образом:
Ответ: 60
245364. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками А и Е1.
Посмотреть решение
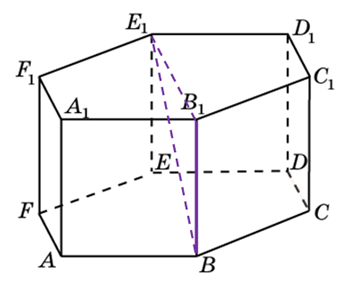
245365. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками В и Е.
Посмотреть решение
245366. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1все ребра равны корню из пяти. Найдите расстояние между точками В и Е1.
Посмотреть решение
245367. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите тангенс угла AD1D.
Посмотреть решение
245368. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите угол DAB. Ответ дайте в градусах.
Посмотреть решение
245369. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите угол AC1C. Ответ дайте в градусах.
Посмотреть решение
На этом всё! Успеха Вам!
В состав ЕГЭ включены и другие задачи по стереометрии, и они довольно разнообразны. Обязательно будем их рассматривать, не пропустите! Успехов вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
В правильной шестиугольной призме найдите расстояние
Дата: 2021-02-13
4271
Категория: Стерео Призма
Метка: ЕГЭ-№2
245364. В правильной шестиугольной призме найдите расстояние между точками A и E1. Все ребра данной призмы ABCDEFA1B1C1D1E1F1 равны 1.

Известна длина ребра AA1, найдём A1 E1. Угол между сторонами правильного шестиугольника равен 120°. По теореме косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними

245365. В правильной шестиугольной призме ABCDEFA1B1 C1D1E1F1 все ребра равны 1. Найдите расстояние между точками B и E.
Рассмотрим правильный шестиугольник:
Искомое расстояние равно диаметру окружности, описанной около правильного шестиугольника со стороной 1. В правильном шестиугольнике сторона равна радиусу описанной окружности, значит BE=2R=2.
Ответ: 2
245366. В правильной шестиугольной призме ABCDEFA1B1 C1D1E1F1 все ребра равны √5. Найдите расстояние между точками B и E1.

Отрезок B1E1 равен двум радиусам описанной около правильного шестиугольника окружности, а радиус описанной окружности равен стороне шестиугольника, то есть

Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.
Ok
|
Как найти расстояние между точками в правильной шестиугольной призме?ksandr97 7 лет назад
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками A и E1. Rafail 7 лет назад Вокруг правильного шестиугольника ABCDEF со сторонами, равными 1 можно описать окружность радиусом 1. Соединим точки ACE. Получился равносторонний треугольник, вписанный в окружность радиуса 1. Сторона такого треугольника √(3). Итак AE=√(3), EE=1. Пифагор нам подсказывает, что AE1=2. автор вопроса выбрал этот ответ лучшим
в избранное
ссылка
отблагодарить ksandr97 Благодарю!
Знаете ответ? |
xeasusth91
ДАНО: АВСDEFA1B1C1D1E1F1 – правильная шестиугольная призма ; АВ = АА1 = 1
НАЙТИ: p ( A ; CB1 )
_________________________
РЕШЕНИЕ:
1) точка А и отрезок СВ1 лежат в плоскости треугольника АВ1С.
Все боковые грани правильной шестиугольной призмы равны.
Значит, АВ1 = В1С => ∆ АВ1С – равнобедренный
Найдём все стороны ∆ АВ1С
2) Рассмотрим ∆ АВ1В ( угол АВВ = 90° ):
По теореме Пифагора:
АВ1² = АВ² + ВВ1²
АВ1² = 1² + 1² = 2
АВ1 = √2
АВ1 = В1С = √2
3) В основании правильной шестиугольной призмы лежит правильный шестиугольник. Все углы правильного шестиугольника равны 120°.
Рассмотрим ∆ АВС ( АВ = ВС ):
По теореме косинусов:
АС² = АВ² + ВС² – 2 × АВ × ВС × cos ABC
AC² = 1² + 1² – 2 × 1 × 1 × cos 120°
AC² = 2 – 2 × ( – 1/2 ) = 2 + 1 = 3
AC = √3
4) B1B перпендикулярен ВН
ВН перпендикулярен АС
Значит, по теореме о трёх перпендикулярах В1Н перпендикулярен АС
Высота в равнобедренном ∆ АВ1С является и медианой и биссектрисой =>
АН = НС = 1/2 × АС = 1/2 × √3 = √3/2
5) Рассмотрим ∆ В1СН ( угол В1НС = 90° ):
По теореме Пифагора:
В1С² = В1Н² + НС²
В1Н² = ( √2 )² – ( √3/2 )² = 2 – 3/4 = 5/4
В1Н = √5/2
Опустим из точки А перпендикуляр АМ на отрезок В1С. Соответственно, АМ = р ( А ; В1С )
6) Найдём площадь ∆ В1АС:
S b1ac = 1/2 × AC × B1H
С другой стороны, S b1ac = 1/2 × B1C × AM
Приравняем площади и получим:
1/2 × АС × В1Н = 1/2 × В1С × АМ
АС × В1Н = В1С × АМ
АМ =
Значит, p ( А ; В1С ) = √30/4
ОТВЕТ: √30 / 4