Как найти расстояние в стоячей воде

Давайте сегодня рассмотрим движение по реке и связанные с этим задачи.

Движение по реке отличается тем, что на движущийся объект воздействует еще и сила течения реки. В реальной жизни и вне реки на нас воздействует ветер, сопротивление воздуха и прочие вещи, но в математике мы этим пренебрегаем.

В задачах на движение по реке важно учитывать направление движения – по течению и против. Если объект в задаче движется по течению, то к его собственной скорости, иногда ее еще называют скоростью в стоячей воде, скоростью в пруду, добавляется скорость реки (течения). Если объект плывет против течения, то скорость реки его сносит назад, поэтому его собственная скорость уменьшается как раз на скорость течения.

Расстояние от пункта A до пункта B по реке равно 120 км. Сколько времени потратит моторная лодка на путь от пункта A до B, если её собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?

Рассмотрите два варианта: 1) лодка движется по течению реки; 2) лодка движется против течения реки.

Решение: Если моторная лодка будет двигаться по течению реки, то её скорость будет равна сумме собственной скорости со скоростью течения реки:

27 + 3 = 30 (км/ч)

Значит расстояние между пунктами лодка преодолеет за:

120 : 30 = 4 (ч)

Если лодка будет двигаться против течения реки, то её скорость будет равна разности собственной скорости и скорости течения реки:

27 – 3 = 24 (км/ч)

Значит, чтобы узнать сколько времени потратит лодка на путь от пункта A до пункта B, надо расстояние разделить на скорость:

120 : 24 = 5 (ч)

Ответ:
1) При движении по течению реки моторная лодка потратит 4 часа на путь от пункта A до пункта B.
2) При движении против течения реки моторная лодка потратит 5 часов на путь от пункта A до пункта B.

Данный материал представляет собой систему
задач по теме “Движение”.

Цель: помочь учащимся более полно овладеть
технологиями решения задач по данной теме.

Задачи на движение по воде.

Очень часто человеку приходится совершать
движения по воде: реке, озеру, морю.

Сначала он это делал сам, потом появились плоты,
лодки, парусные корабли. С развитием техники
пароходы, теплоходы, атомоходы пришли на помощь
человеку. И всегда его интересовали длина пути и
время, затраченное на его преодоление.

Представим себе, что на улице весна. Солнце
растопило снег. Появились лужицы и побежали
ручьи. Сделаем два бумажных кораблика и пустим
один из них в лужу, а второй – в ручей. Что же
произойдет с каждым из корабликов?

В луже кораблик будет стоять на месте, а в
ручейке – поплывет, так как вода в нем “бежит”
к более низкому месту и несет его с собой. То же
самое будет происходить с плотом или лодкой.

В озере они будут стоять на месте, а в реке –
плыть.

Рассмотрим первый вариант: лужа и озеро. Вода в
них не движется и называется стоячей.

Кораблик поплывет по луже только в том случае,
если мы его подтолкнем или если подует ветер. А
лодка начнет двигаться в озере при помощи весел
или если она оснащена мотором, то есть за счет
своей скорости. Такое движение называют движением
в стоячей воде.

Отличается ли оно от движения по дороге? Ответ:
нет. А это значит, что мы с вами знаем как
действовать в этом случае.

Задача 1. Скорость катера по озеру равна 16 км/ч.

Какой путь пройдет катер за 3 часа?

Ответ: 48 км.

Следует запомнить, что скорость катера в
стоячей воде называют собственной скоростью.

Задача 2. Моторная лодка за 4 часа проплыла по
озеру 60 км.

Найдите собственную скорость моторной лодки.

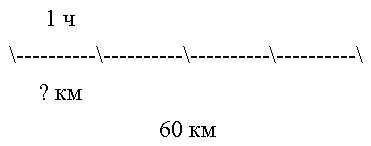
Ответ: 15 км/ч.

Задача 3. Сколько времени потребуется лодке,
собственная скорость которой

равна 28 км/ч, чтобы проплыть по озеру 84 км?

Ответ: 3 часа.

Итак, чтобы найти длину пройденного пути,
необходимо скорость умножить на время.

Чтобы найти скорость, необходимо длину пути
разделить на время.

Чтобы найти время, необходимо длину пути
разделить на скорость.

Чем же отличается движение по озеру от
движения по реке?

Вспомним бумажный кораблик в ручье. Он плыл,
потому что вода в нем движется.

Такое движение называют движением по течению.
А в обратную сторону –  движением против
течения.

Итак, вода в реке движется, а значит имеет свою
скорость. И называют ее скоростью течения реки.
( Как ее измерить?)

Задача 4. Скорость течения реки равна 2 км/ч. На
сколько километров река относит

любой предмет (щепку, плот, лодку) за 1час, за 4
часа?

Ответ: 2 км/ч, 8 км/ч.

Каждый из вас плавал в реке и помнит, что по
течению плыть гораздо легче, чем против течения.
Почему? Потому, что в одну сторону река
“помогает” плыть, а в другую – “мешает”.

Рис.1

Те же, кто не умеет плавать, могут представить
себе ситуацию, когда дует сильный ветер.
Рассмотрим два случая:

1) ветер дует в спину,

2) ветер дует в лицо.

И в том и в другом случае идти сложно. Ветер в
спину заставляет бежать, а значит, скорость
нашего движения увеличивается. Ветер в лицо
сбивает нас, притормаживает. Скорость при этом
уменьшается.

Остановимся на движении по течению реки. Мы уже
говорили о бумажном кораблике в весеннем ручье.
Вода понесет его вместе с собой. И лодка,
спущенная на воду, поплывет со скоростью течения.
Но если у нее есть собственная скорость, то она
поплывет еще быстрее.

Следовательно, чтобы найти скорость движения
по течению реки, необходимо сложить собственную
скорость лодки и скорость течения.

Задача 5. Собственная скорость катера равна 21
км/ч, а скорость течения реки 4 км/ч. Найдите
скорость катера по течению реки.

Ответ: 25км/ч.

Теперь представим себе, что лодка должна плыть
против течения реки. Без мотора или хотя бы весел,
течение отнесет ее в обратную сторону. Но, если
придать лодке собственную скорость ( завести
мотор или посадить гребца), течение будет
продолжать отталкивать ее назад и мешать
двигаться вперед со своей скоростью.

Поэтому, чтобы найти скорость лодки против
течения, необходимо из собственной скорости
вычесть скорость течения.

Задача 6. Скорость течения реки равна 3 км/ч, а
собственная скорость катера 17 км/ч.

Найдите скорость катера против течения.

Ответ: 14 км/ч.

Задача 7. Собственная скорость теплохода равна
47,2 км/ч, а скорость течения реки 4,7 км/ч. Найдите
скорость теплохода по течению и против течения.

Ответ: 51,9 км/ч; 42,5 км/ч.

Задача 8. Скорость моторной лодки по течению
равна12,4 км/ч. Найдите  собственную скорость
лодки, если скорость течения реки 2,8 км/ч.

Ответ: 9,6 км/ч.

Задача 9. Скорость катера против течения равна
10,6 км/ч. Найдите собственную скорость катера и
скорость по течению, если скорость течения реки
2,7 км/ч.

Ответ: 13,3 км/ч; 16 км/ч.

Связь между скоростью по течению и
скоростью против течения.

Введем следующие обозначения:

V_с. – собственная скорость,

V_теч. – скорость течения,

V _{по теч.} – скорость по течению,

V _пр.теч. – скорость против течения.

Тогда можно записать следующие формулы:

V _{no теч} ⁼ V_c + V_теч ;

V _{np. теч} ⁼ V_c – V _теч.;

Попытаемся изобразить это графически:

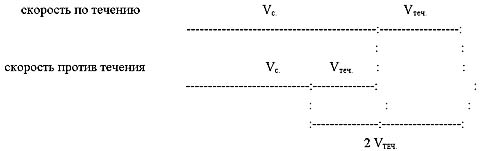
Рис. 2

Вывод: разность скоростей по течению
и против течения  равна удвоенной скорости
течения.

Vno теч — Vnp. теч = 2 Vтеч.

Vтеч = (V по теч – Vnp. теч ): 2

Задача.

1) Скорость катера против течения равна 23 км/ч, а
скорость течения 4 км/ч.

Найдите скорость катера по течению.

Ответ: 31 км/ч.

2) Скорость моторной лодки по течению реки равна
14 км/ч/ а скорость течения 3 км/ч. Найдите скорость
лодки против течения

Ответ: 8 км/ч.

Задача 10. Определите скорости и заполните
таблицу:

	V С.	Vтеч.	Vпо теч.	Vпр.теч.
1	12 км/ч	3 км/ч
2	23 км/ч		25 км/ч
3	24 км/ч			20 км/ч
4		4 км/ч	17 км/ч:
5		5 км/ч		18 км/ч
6			42 км/ч	34 км/ч

* – при решении п.6 смотри рис.2.

Ответ: 1) 15 и 9; 2) 2 и 21; 3) 4 и 28; 4) 13 и 9; 5)23 и 28; 6) 38 и 4.

Через уравнение.

S – пройденный путь, растояние, которое прошла, например, лодка. (км)

t – время, за которое она прошла расстояние S. (часов, минут)

V – собственная её скорость (км/ч, м/ч)

Такие задачи решаются далее: если известны: (под формулы подставляем числа)

t и V, то перемножаем – t * V, получаем S.

t и S, то расстояние делим время – S : t, получаем V

S и V, также – S : V, получаем t

Также если в задаче указана V (её ищем)

по течению, то V собственная + V по течению

против течения, то V собств. – V прот. теч.

Тогда формулы звучат так: если известны:

t и V, то t * (V с. +/- V) = S

t и S, то S : t = V с. +/- V

V и S, то S : (V c. +/- V) = t

Теперь ещё раз:

V c. – собственная скорость

V c. + V – скорость + скорость по теч.

V c. – V – скорость + скорость прот. теч.

Ну так чтоли… Плохой из меня учитель(((

Решение задач с помощью уравнений.
Движение по воде.

ФОРМУЛЫ.

V
соб. – собственная скорость (скорость в стоячей
воде)

Vтеч.р.
– скорость течения реки

Vпо
теч. = V соб. + Vтеч.р.

Vпр.
теч. = V соб. – Vтеч.р.

Задача
1. Лодка
плыла 1,4
ч по течению реки и 1,7 ч против течения. Путь,
который проплыла лодка по течению, оказался на 2,2 км меньше пути, который она
проплыла против течения. Найдите скорость
течения реки, если скорость лодки в стоячей воде 28 км/ч.

	V (км/ч)	t (ч)	S (км)
По течению	28 + x	1,4	1,4(28 + x)
Против течения	28 – x	1,7	1,7(28 – x)

V соб. = 28 км/ч

Vтеч.р. = x км/ч

1)     
1,7(28 – x) – 1,4(28 + x) = 2,2

47,6 – 1,7x – 39,2  – 1,4x = 2,2

-1,7x – 1,4x= 2,2 – 47,6 +39,2

-3,1x = -6,2

x = -6,2 : (-3,1)

x = 2

2)     
2 км/ч – Vтеч.р.

Ответ. 2

Задача
2. Расстояние между двумя пунктами катер прошёл по течению реки за 7
часов, а против течения за 8 часов. Найдите расстояние
между этими пунктами, если скорость течение реки 3,5 км/ч

	V (км/ч)	t (ч)	S (км)
По течению	x + 3,5	7	7(x + 3,5)
Против течения	x – 3,5	8	8(x – 3,5)

V соб. = x км/ч

Vтеч.р. = 3,5 км/ч

1)     
7(x + 3,5) = 8(x – 3,5)

7x + 24,5 = 8x – 28

7x – 8x= -28 – 24,5

-x = -52,5

x = 52,5

2)   52,5 км/ч – V
соб.

3)   7(52,5 + 3,5) = 7 · 56 = 392 км –
расстояние

Ответ. 392

РЕШИ ЗАДАЧИ ПО ОБРАЗЦУ.

1)      Туристы на байдарке плыли
2,4 ч по течению реки и 1,8 ч против течения. Путь, который байдарка проплыла
по течению, был на 14,1 км больше, чем путь, пройденный против течения. Найдите
скорость байдарки в стоячей воде, если скорость течения 2,5 км/ч.

2)      Расстояние между двумя
пунктами катер прошел по течению реки за 5 часов, а против течения – за 6
часов. Найдите расстояние между этими пунктами, если скорость течения реки 3
км/ч.

3)      Катер
проходит по течению реки за 5 ч такое же расстояние, как за 6 ч 15 мин против
течения. Найдите скорость катера в стоячей воде, если скорость течения реки
равна 2,4 км/ч.

4)      Моторная
лодка прошла 7 ч по течению реки и 6 ч против течения. Определите скорость
течения реки, если скорость лодки в стоячей воде 10
км/ч и за все путешествие лодка прошла 132
км.