Skip to content
Длина вектора в пространстве
Длиной (или модулем) вектора называется расстояние между началом и концом вектора.
Длина вектора a{X,Y,Z} выражается через его координаты следующей формулой:
![]()
Пример
Длина вектора $aleft{ { — 2,3,sqrt 3 } right}$ равна
$left| a right| = sqrt {{X^2} + {Y^2} + {Z^2}} = $
$sqrt {{{left( { — 2} right)}^2} + {3^2} + {{left( {sqrt 3 } right)}^2}} = sqrt {16} = 4$
Расстояние между двумя точками в пространстве
Расстояние d между точками в пространстве A1{x1;y1;z1}, A2{x2;y2;z2} представляется формулой
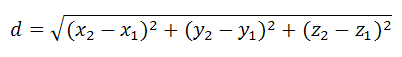
Пример
Расстояние между точками A1{4;-6;3} и A2 {-1;5;-4}
$d = sqrt {{{left( {{x_2} — {x_1}} right)}^2} + {{left( {{y_2} — {y_1}} right)}^2} + {{left( {{z_2} — {z_1}} right)}^2}} = $
$=sqrt {{{left( { — 1 — 4} right)}^2} + {{left( {5 — left( { — 6} right)} right)}^2} + {{left( { — 4 — 3} right)}^2}} =$
$ =sqrt {25 + 121 + 49} = sqrt {195} approx 14$
![]() 12670
12670
Расстояние d между точками в пространстве A11;y1;z1>, A22;y2;z2> представляется формулой
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.3 / 5. Количество оценок: 8
Оценок пока нет. Поставьте оценку первым.
3 комментария
найти расстояние между точками с(-2;1;-2) д (-1;2;1) м (-1;0;2) н (1;-1;2) найти 3 вектора сд — 2 вектора мн
Как найти расстояние вектора по координатам двух точек
Найдем расстояние между двумя точками a и b. (длину отрезка)
По сути каждая координата точки – это вектор. Ниже будет надо будет ввести координаты векторов (точек).
Надо Вам ввести лишь размерность (допустим, если точки на плоскости, то размерность равна 2, если в пространстве, то 3) и координаты точек. А система уже сама вычислит длину отрезка (расстояние между точками).
Сервис выдаёт не только ответ, но ещё и готовое решение
Точки a(2,2,-1) и b(1,4,8), тогда число координат равно 3.
© Контрольная работа РУ – калькуляторы онлайн
Где учитесь?
Для правильного составления решения, укажите:
Расстояние от точки до точки: формулы, примеры, решения
В данной статье рассмотрим способы определить расстояние от точки до точки теоретически и на примере конкретных задач. И для начала введем некоторые определения.
Расстояние между точками – это длина отрезка, их соединяющего, в имеющемся масштабе. Задать масштаб необходимо, чтобы иметь для измерения единицу длины. Потому в основном задача нахождения расстояния между точками решается при использовании их координат на координатной прямой, в координатной плоскости или трехмерном пространстве.
Расстояние между точками на координатной прямой
Исходные данные: координатная прямая O x и лежащая на ней произвольная точка А . Любой точке прямой присуще одно действительное число: пусть для точки А это будет некое число х A , оно же – координата точки А .
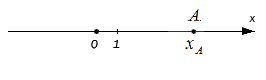
В целом можно говорить о том, что оценка длины некого отрезка происходит в сравнении с отрезком, принятым за единицу длины в заданном масштабе.
Если точке А соответствует целое действительное число, отложив последовательно от точки О до точки по прямой О А отрезки – единицы длины, мы можем определить длину отрезка O A по итоговому количеству отложенных единичных отрезков.
К примеру, точке А соответствует число 3 – чтобы попасть в нее из точки О , необходимо будет отложить три единичных отрезка. Если точка А имеет координату – 4 – единичные отрезки откладываются аналогичным образом, но в другом, отрицательном направлении. Таким образом в первом случае, расстояние О А равно 3 ; во втором случае О А = 4 .
Если точка A имеет в качестве координаты рациональное число, то от начала отсчета (точка О ) мы откладываем целое число единичных отрезков, а затем его необходимую часть. Но геометрически не всегда возможно произвести измерение. К примеру, затруднительным представляется отложить на координатной прямой дробь 4 111 .
Вышеуказанным способом отложить на прямой иррациональное число и вовсе невозможно. К примеру, когда координата точки А равна 11 . В таком случае возможно обратиться к абстракции: если заданная координата точки А больше нуля, то O A = x A (число принимается за расстояние); если координата меньше нуля, то O A = – x A . В общем, эти утверждения справедливы для любого действительного числа x A .
Резюмируя: расстояние от начала отсчета до точки, которой соответствует действительное число на координатной прямой, равно:
- 0, если точка совпадает с началом координат;
- x A , если x A > 0 ;
- – x A , если x A 0 .
При этом очевидно, что сама длина отрезка не может быть отрицательной, поэтому, используя знак модуля, запишем расстояние от точки O до точки A с координатой x A : O A = x A
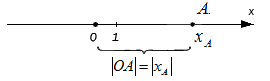
Верным будет утверждение: расстояние от одной точки до другой будет равно модулю разности координат. Т.е. для точек A и B , лежащих на одной координатной прямой при любом их расположении и имеющих соответственно координаты x A и x B : A B = x B – x A .
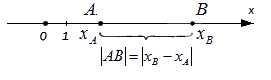
Расстояние между точками на плоскости
Исходные данные: точки A и B , лежащие на плоскости в прямоугольной системе координат O x y с заданными координатами: A ( x A , y A ) и B ( x B , y B ) .
Проведем через точки А и B перпендикуляры к осям координат O x и O y и получим в результате точки проекции: A x , A y , B x , B y . Исходя из расположения точек А и B далее возможны следующие варианты:
– если точки А и В совпадают, то расстояние между ними равно нулю;
– если точки А и В лежат на прямой, перпендикулярной оси O x (оси абсцисс), то точки и совпадают, а | А В | = | А y B y | . Поскольку, расстояние между точками равно модулю разности их координат, то A y B y = y B – y A , а, следовательно A B = A y B y = y B – y A .
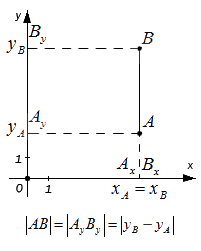
– если точки A и B лежат на прямой, перпендикулярной оси O y (оси ординат) – по аналогии с предыдущим пунктом: A B = A x B x = x B – x A
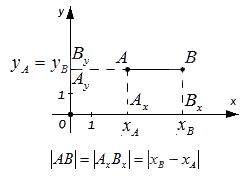
– если точки A и B не лежат на прямой, перпендикулярной одной из координатных осей, найдем расстояние между ними, выведя формулу расчета:
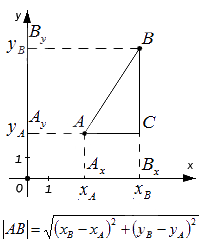
Мы видим, что треугольник А В С является прямоугольным по построению. При этом A C = A x B x и B C = A y B y . Используя теорему Пифагора, составим равенство: A B 2 = A C 2 + B C 2 ⇔ A B 2 = A x B x 2 + A y B y 2 , а затем преобразуем его: A B = A x B x 2 + A y B y 2 = x B – x A 2 + y B – y A 2 = ( x B – x A ) 2 + ( y B – y A ) 2
Сформируем вывод из полученного результата: расстояние от точки А до точки В на плоскости определяется расчётом по формуле с использованием координат этих точек
A B = ( x B – x A ) 2 + ( y B – y A ) 2
Полученная формула также подтверждает ранее сформированные утверждения для случаев совпадения точек или ситуаций, когда точки лежат на прямых, перпендикулярных осям. Так, для случая совпадения точек A и B будет верно равенство: A B = ( x B – x A ) 2 + ( y B – y A ) 2 = 0 2 + 0 2 = 0
Для ситуации, когда точки A и B лежат на прямой, перпендикулярной оси абсцисс:
A B = ( x B – x A ) 2 + ( y B – y A ) 2 = 0 2 + ( y B – y A ) 2 = y B – y A
Для случая, когда точки A и B лежат на прямой, перпендикулярной оси ординат:
A B = ( x B – x A ) 2 + ( y B – y A ) 2 = ( x B – x A ) 2 + 0 2 = x B – x A
Расстояние между точками в пространстве
Исходные данные: прямоугольная система координат O x y z с лежащими на ней произвольными точками с заданными координатами A ( x A , y A , z A ) и B ( x B , y B , z B ) . Необходимо определить расстояние между этими точками.
Рассмотрим общий случай, когда точки A и B не лежат в плоскости, параллельной одной из координатных плоскостей. Проведем через точки A и B плоскости, перпендикулярные координатным осям, и получим соответствующие точки проекций: A x , A y , A z , B x , B y , B z
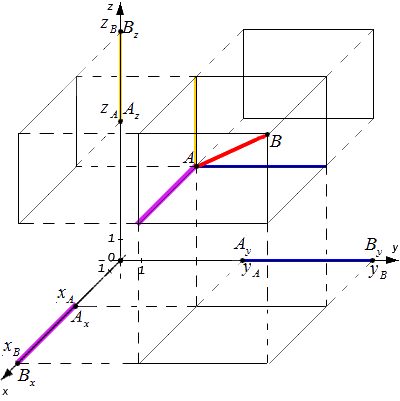
Расстояние между точками A и B являет собой диагональ полученного в результате построения параллелепипеда. Согласно построению измерения этого параллелепипеда: A x B x , A y B y и A z B z
Из курса геометрии известно, что квадрат диагонали параллелепипеда равен сумме квадратов его измерений. Исходя из этого утверждения получим равенство: A B 2 = A x B x 2 + A y B y 2 + A z B z 2
Используя полученные ранее выводы, запишем следующее:
A x B x = x B – x A , A y B y = y B – y A , A z B z = z B – z A
A B 2 = A x B x 2 + A y B y 2 + A z B z 2 = x B – x A 2 + y B – y A 2 + z B – z A 2 = = ( x B – x A ) 2 + ( y B – y A ) 2 + z B – z A 2
Итоговая формула для определения расстояния между точками в пространстве будет выглядеть следующим образом:
A B = x B – x A 2 + y B – y A 2 + ( z B – z A ) 2
Полученная формула действительна также для случаев, когда:
– лежат на одной координатной оси или прямой, параллельной одной из координатных осей.
Примеры решения задач на нахождение расстояния между точками
Исходные данные: задана координатная прямая и точки, лежащие на ней с заданными координатами A ( 1 – 2 ) и B ( 11 + 2 ) . Необходимо найти расстояние от точки начала отсчета O до точки A и между точками A и B .
Решение
- Расстояние от точки начала отсчета до точки равно модулю координаты этой точки, соответственно O A = 1 – 2 = 2 – 1
- Расстояние между точками A и B определим как модуль разности координат этих точек: A B = 11 + 2 – ( 1 – 2 ) = 10 + 2 2
Ответ: O A = 2 – 1 , A B = 10 + 2 2
Исходные данные: задана прямоугольная система координат и две точки, лежащие на ней A ( 1 , – 1 ) и B ( λ + 1 , 3 ) . λ – некоторое действительное число. Необходимо найти все значения этого числа, при которых расстояние А В будет равно 5 .
Решение
Чтобы найти расстояние между точками A и B , необходимо использовать формулу A B = ( x B – x A ) 2 + y B – y A 2
Подставив реальные значения координат, получим: A B = ( λ + 1 – 1 ) 2 + ( 3 – ( – 1 ) ) 2 = λ 2 + 16
А также используем имеющееся условие, что А В = 5 и тогда будет верным равенство:
λ 2 + 16 = 5 λ 2 + 16 = 25 λ = ± 3
Ответ: А В = 5 , если λ = ± 3 .
Исходные данные: задано трехмерное пространство в прямоугольной системе координат O x y z и лежащие в нем точки A ( 1 , 2 , 3 ) и B – 7 , – 2 , 4 .
Решение
Для решения задачи используем формулу A B = x B – x A 2 + y B – y A 2 + ( z B – z A ) 2
Подставив реальные значения, получим: A B = ( – 7 – 1 ) 2 + ( – 2 – 2 ) 2 + ( 4 – 3 ) 2 = 81 = 9
[spoiler title=”источники:”]
http://www.kontrolnaya-rabota.ru/s/vector/rasstoyanie-mezhdu-tochkami/
http://zaochnik.com/spravochnik/matematika/vektory/rasstojanie-mezhdu-tochkami/
[/spoiler]
Если
нам известны координаты точек (естественно,
в заданной системе координат), то
однозначно известно их положение.
Поэтому можно найти любые геометрические
характеристики их взаимного расположения.
Получим формулы, позволяющие по известным
координатам двух точек вычислить
расстояние между ними.
В
простейшем случае, когда две
точки А1 и А2 находятся
на одной оси, расстояние между ними
определяется формулой
s
= |x2 −
x1|,
(3)
где х1, х2 −
координаты точек А1 и А2 соответственно.
Очевидно,
что расстояние от А1 до А2 равно
расстоянию от А2 до А1,
что и привело у к тому, что в формуле (3)
появился знак модуля числа.
Пусть
на плоскости задана система координат ХОY,
в которой координаты точки А1 равны х1 и у1,
а координаты точки А2,
соответственно, равны х2 и у2 (рис.
8).

рис.
8
В
прямоугольном треугольнике А1А2В длина
стороны А2В равна |х2 −
х1|,
а длина стороны А1В
= |у2 −
у1|,
поэтому расстояние между точками А1 и А2 можно
найти по теореме Пифагора:
s
= √{(x2 −
x1)2 +
(y2 −
y1)2}.
(4)
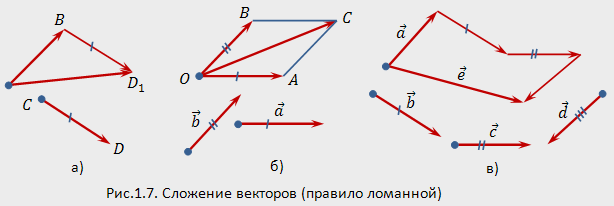
26. Линейные операции над векторами. Линейные операции над векторами
Сложение
векторов
Пусть
даны два вектора ![]()
и ![]()
.
Приложим вектор
к
точке
(концу
вектора
)
и получим вектор ![]()
(рис.1.7,а;
здесь и далее равные векторы отмечены
одинаковыми засечками).
Вектор ![]()
называется суммой
векторов
и
и
обозначается ![]()
.
Это нахождение суммы называется правилом
треугольника.
Сумму
двух неколлинеарных векторов ![]()
и ![]()
можно
найти по правилу
параллелограмма.
Для этого откладываем от любой
точки
векторы ![]()
и ![]()
,
а затем строим параллелограмм ![]()
(рис.
1.7,6). Диагональ ![]()
параллелограмма
определяет сумму: ![]()
.
Для
нахождения суммы нескольких векторов
можно построить ломаную из равных им
векторов. Тогда замыкающий
вектор,
соединяющий начало первого вектора
ломаной с концом последнего ее вектора,
равен сумме всех векторов ломаной. На
рис.1.7,в изображена сумма ![]()
четырех
векторов ![]()
.
Таким способом (правило
ломаной)
можно сложить любое конечное число
векторов. Заметим, что сумма векторов
не зависит от точек приложения слагаемых
и от порядка суммирования. Например,
“выстраивая цепочку” векторов для
суммы в виде ![]()
,
получим вектор, равный вектору ![]()
.
Если ломаная получилась замкнутой, то
сумма равна нулевому вектору.

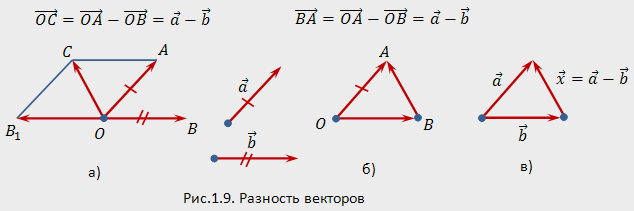
Вычитание
векторов
Вектор ![]()
называется противоположным вектору
,
если их сумма равна нулевому вектору: ![]()
.
Противоположный вектор ![]()
имеет
длину ![]()
,
коллинеарен и противоположно направлен
вектору
(рис.1.8,а,б).
Нулевой вектор является противоположным
самому себе.

Разностью
векторов
и
называется
сумма вектора
с
вектором ![]()
,
противоположным вектору
:
![]()
Для
нахождения разности векторов
и
приложим
к произвольной точке
векторы ![]()
,
а также вектор ![]()
,
противоположный вектору
(рис.1.9,а).
Искомую разность находим по правилу
параллелограмма:
Для
нахождения разности проще использовать
правило треугольника (рис. 1.9,6). Для этого
прикладываем к произвольной
точке
векторы
.
Вектор ![]()
при
этом равен искомой разности ![]()
.
Вычитание
векторов — действие, обратное сложению
— можно определить также следующим
образом: разностью
векторов
и
называется
такой вектор ![]()
,
который в сумме с вектором
дает
вектор
(рис.1.9,в),
т.е. разность ![]()
—
это решение уравнения ![]()
.
Пример
1.2. Для
векторов на рис. 1.6 найти следующие суммы
и разности:
Решение. Учитывая
равенство ![]()
,
получаем по правилу треугольника ![]()
.
Поскольку ![]()
и ![]()
,
то ![]()
.
По
правилу параллелограмма ![]()
.
Так
как ![]()
и ![]()
,
находим
Умножение
вектора на число
Произведением
ненулевого вектора а на действительное
число ![]()
называется
вектор ![]()
,
удовлетворяющий условиям:
1)
длина вектора
равна ![]()
,
т.е. ![]()
;
2)
векторы
и
коллинеарные ![]()
;
3)
векторы
и
одинаково
направлены, если ![]()
,
и противоположно направлены, если ![]()
.
Произведение
нулевого вектора на любое число ![]()
считается
(по определению) нулевым вектором: ![]()
;
произведение любого вектора на число
нуль также считается нулевым вектором: ![]()
.
Из определения произведения следует,
что:
а)
при умножении на единицу ![]()
вектор
не изменяется: ![]()
;
б)
при умножении вектора на ![]()
получается
противоположный вектор: ![]()
;
в) деление
вектора на отличное от нуля число ![]()
сводится
к его умножению на число ![]()
,
обратное ![]()
.
г)
при делении ненулевого вектора
на
его длину, т.е. при умножении
на
число ![]()
получаем
единичный вектор, одинаково направленный
с вектором
.
Действительно,
длина вектора ![]()
равна
единице: ![]()
.
Вектор
коллинеарен
и одинаково направлен с вектором
,
так как ![]()
;
д)
при умножении единичного вектора на
число
получаем
коллинеарный ему вектор, длина которого
равна ![]()
.
На
рис.1.10 изображены векторы, получающиеся
в результате умножения данного
вектора
на ![]()
и ![]()
,
а также противоположный вектор ![]()
.

Свойства
линейных операций над векторами
Сложение
векторов и умножение вектора на число
называются линейными
операциями над векторами.
Для
любых векторов ![]()
и
любых действительных чисел ![]()
справедливы
равенства:
Свойства
1, 2 выражают коммутативность и
ассоциативность операции сложения
векторов, свойство 5 — ассоциативность
операции умножения на число, свойства
6,7 — законы дистрибутивности, свойство
8 называется унитарностью.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
План урока:
Прямоугольная система координат
Координаты вектора
Координаты середины отрезка
Вычисление длины векторов и расстояния между точками
Коллинеарность векторов
Определение компланарности векторов
Скалярное произведение векторов
Прямоугольная система координат
В планиметрии мы уже рассматривали прямоугольную систему координат. Ее образовывали 2 перпендикулярные друг другу оси – Ох и Оу. С ее помощью можно было определить положение любой точки на координатной плоскости, просто указав две ее координаты – абсциссу х и ординату у.
В стереометрии необходимо определять положение точки уже не на плоскости, а в пространстве. Для этого добавляется третья ось Оz, которую ещё называют осью апликат. Каждые пара осей образует свою отдельную координатную плоскость, всего получается три таких плос-ти: Оху, Охz и Oуz.

Точка О именуется началом координат. Она делит каждую ось на два луча, один из которых – это положительная полуось, а второй – отрицательная полуось.
Для каждой точки в пространстве можно указать три координаты, однозначно определяющие ее положение в пространстве. Пусть в пространстве есть некоторая точка М. Опустим из нее перпендикуляры на координатные плоскости. В свою очередь из этих проекций точки М опустим перпендикуляры уже на координатные оси. В результате будет построен прямоугольный параллелепипед. Измерения этого параллелепипеда и будут координатами точки М:

Если точка M находится в одной из координатных плоскостей, то одна из ее координат будет нулевой. Например, если М принадлежит плоскости Охz, то нулю будет равна координата у. Если же точка располагается на одной из координатных осей, то у нее уже две координаты будут нулевыми. Так, если точка находится на оси Ох, то только координата х может быть ненулевой, а у и z окажутся нулевыми координатами.
На показанном рисунке ребра параллелепипеда лежат на положительных полуосях, поэтому все координаты положительны. Если же какие-то ребра будут лежать на отрицательных полуосях, то и соответствующие координаты будут отрицательными.
Координаты вектора
Введем в пространстве прямоугольную систему коорд-т, а далее от ее начала отложим вектора i, j и k, которые соответственно будут лежать на координатных осях Ох, Оу и Оz, и длина которых составит единицу. Эти вектора именуют координатными векторами, единичными векторами или просто ортами.

Ясно, что орты находятся в разных плоскостях, то есть они образуют тройку некомпланарных векторов. Это означает, что любой вектор а в пространстве можно разложить на орты:

где х, у и z – какие-то действительные числа. Они как раз и считаются координатами вектора а. Записываются коорд-ты вектора в фигурных скобках. На следующем рисунке показан вектор а{3; – 2; – 4}.

Задание. Разложите на орты вектор

Если начало вектора ОМ располагается в начале системы координат О, то вектор ОМ именуют радиус-вектором. В таком случае коорд-ты точки конца вектора, то есть точки М, совпадают с коорд-тами самого вектора ОМ.

Это свойство радиус-вектора мы уже изучали в 9 классе в планиметрии, и в стереометрии оно сохраняется.
Задание. О – начало координат, а точка М имеет коорд-ты (2; 5; – 3). Найдите коорд-ты вектора ОМ.
Решение. Всё очень просто – коорд-ты вектора будут совпадать с коорд-тами его конца, так его начало совпадает с началом коорд-т:

Также в стереометрии остаются справедливыми ещё несколько правил, которые были доказаны в курсе планиметрии:

Задание. Найдите сначала сумму, а потом разность векторов а{3; 7; 5} и b{2; 4; 6}.
Решение. Будем обозначать коорд-ты векторов через индексы. Например, коорд-ты вектора а – это ха, уа и zа. Пусть сумма векторов будет вектором с, а их разность – вектором d. Для вычисления суммы надо складывать соответствующие координаты:

Для вычисления разности надо из коорд-т вектора а вычитать коорд-ты вектора b:

Задание. Вычислите коорд-ты вектора р, зная, что:

Решение. Для вычисления координат надо в выражении для вектора р сами векторы заменить на их координаты:

Получается, что вектор p имеет координаты {0; – 2; 3}.
Теперь мы можем доказать ещё одно утверждение, уже известное из курса планиметрии:

Действительно, пусть есть некоторый вектор АВ, причем коорд-ты точек А и В известны. Построим радиус-вектора OА и OВ:

Координаты радиус-векторов будут совпадать с координатами их концов:

ч. т. д.
Задание. Определите коорд-ты вектора CD, если даны коорд-ты точек С и D: С(3; 8; – 5) и D(5; 4; 1).
Решение. Здесь надо просто из коорд-т точки D, являющейся концом вектора, вычесть коорд-ты точки С:

Задание. От точки K(10; 6; 13) отложен вектор m{3; 2; 5}, конец совпал в точку H. Найдите коорд-ты точки H.
Решение. Коорд-ты вектора m и его концов связаны формулами:

Координаты середины отрезка
Пусть в пространстве есть отрезок АВ, и координаты его концов известны. Точка М – середина этого отрезка. Как вычислить ее координаты? Рассмотрим взаимосвязь векторов АМ, МВ и АВ:

Раз М – середина АВ, то вектора АМ и МВ имеют равные длины, и при этом они находятся на одной прямой. Значит, эти вектора равны и потому у них одинаковые коорд-ты:

Аналогично можно получить аналогичные формулы для коорд-т у и z:


Рассмотрим несколько задач на координаты точек.
Задание. Найдите коорд-ты середины отрезка, соединяющего точки А(3; 7; 12) и В(1; 5; – 4).
Решение. Просто используем только что выведенные формулы. Середину также обозначаем буквой М:

Задание. Известно, что K середина отрезка CD. Даны координаты точек С и K: С(12; 9; – 3) и K(15; 7; 3). Найдите коорд-ты D.
Решение. Сначала запишем формулу для коорд-ты х:

Вычисление длины векторов и расстояния между точками
Рассмотрим радиус-вектор ОМ с коорд-тами {x; у; z}. Попытаемся найти его длину. Мы можем построить прямоугольный параллелепипед, в котором этот вектор окажется диагональю:

Напомним, что квадрат длины диагонали в прямоугольном параллелепипеде равен сумме квадратов его измерений. Но в полученном параллелепипеде измерения – это коорд-ты х, у и z, поэтому можно записать:

Так как равные вектора имеют как одинаковы и коорд-ты, и длина, то ясно, что каждый вектор с коорд-тами {x; y; z} будет равен рассмотренному радиус-вектору, а значит и его длина будет рассчитываться по такой же формуле.

Задание. Найдите длину вектора m{– 2; 9; 6}.
Решение. Просто используем формулу:

Рассмотрим отрезок АВ с известными коорд-тами его концов. Можно построить вектор АВ, его коорд-ты будут определяться так:


Задание. Найдите расстояние между точкой K(10; 15; 5) и M(16; 21; – 2).
Решение. Просто подставляем коорд-ты точек в формулу:

Задание. Найдите длину медианы KM в ∆ KPN, если известны коорд-ты его вершин: P(2; 5; 8), N (6; 9; 12) и K(16; 11; 13).
Решение. Для нахождения длины медианы достаточно знать коорд-ты ее концов. Коорд-ты K уже известны, а M – середина PN, что позволяет вычислить и ее коорд-ты:

Коллинеарность векторов
Напомним, что если два вектора а и b коллинеарны друг другу, то должно существовать такое число k, что


Полученное отношение (1) является одновременно и признаком коллинеарных векторов, и их свойством. Слово «признак» означает, что любые вектора, чьи координаты соответствуют условию (1), будут коллинеарны. Слово «свойство» означает обратное – если известно, что вектора коллинеарны, то для них обязательно выполняется условие (1). В таких случаях в математике может использоваться словосочетание «тогда и только тогда»:

Очень важно то, что это правило действует только в случае, если все коорд-ты векторов ненулевые. Теперь рассмотрим случай, когда какие-то коорд-ты вектора b (одна или две из них) равны нулю. Например, пусть

В результате мы выяснили, что если коорд-та одного вектора нулевая, то и у любого вектора, коллинеарному ему, эта же коорд-та также должна быть нулевой. Особняком стоит случай с нулевым вектором с коорд-тами {0; 0; 0}. Он условно признается коллинеарным любому вектору.
Задание. Выясните, какие из этих пар векторов коллинеарны:

Решение. В первом задании просто делим друг на друга соответствующие коорд-ты и находим значение коэффициента k:

Значение коэффициента k оказалось одинаковым для каждой пары коорд-т, значит, вектора коллинеарны.
Повторяем эти действия в задании б):

На этот раз коэффициенты k оказались различными, значит, вектора неколлинеарны.
В задании в) у вектора е коорд-та z нулевая. Значит, если и у вектора f, если он коллинеарен z, эта координата должна быть нулевой, но это не так. Значит, вектора e и f неколлинеарны.
В задании г) снова указаны вектора с нулевыми коорд-тами. Но у обоих векторов коорд-та z нулевая, поэтому они могут быть коллинеарными. Однако необходимо проверить, что отношение ненулевых координат одинаково:

Коэффициент k получился одинаковым, поэтому вектора коллинеарны.
В последнем задании д) вектор n – нулевой, ведь все его коорд-ты нулевые. Нулевой вектор всегда коллинеарен другим векторам, в том числе и в этом задании.
Ответ: а) да; б) нет; в) нет; г) да; д) да.
Задание. Выясните, располагаются ли на одной прямой точки А(3; 5; 12), В(5; 7; 16) и С(0; 2; 6).
Решение. Ясно, что если эти точки находятся на одной прямой, то вектора АВ и ВС будут коллинеарными. Если же эти вектора неколлинеарны, то и точки должны находиться на разных прямых.
Сначала вычислим коорд-ты векторов АВ и ВС:

Теперь проверяем, коллинеарны ли эти вектора:

Коэффициенты k одинаковы, а потому АВ и ВС – коллинеарные векторы. Значит, точки А, В и С находятся на одной прямой.
Определение компланарности векторов
Пусть у нас есть три вектора с известными коорд-тами:

Как определить, компланарны ли эти вектора, то есть располагаются ли они в одной плоскости? Если эти вектора компланарны, то, по признаку компаланарности, вектор а можно разложить на вектора b и с:

где х и y – некоторые числа. Но если такое разложение существует, то коорд-ты векторов а, b и с будут связаны равенствами:

Получили систему из 3 уравнений с двумя неизвестными (х и y). Если такая система имеет решение, то вектора компланарны. Если же решения нет, то вектора не компланарны.
Задание. Определите, компланарны ли вектора


Имеем систему с тремя уравнениями. Из последних двух уравнений очевидно, что его решением может быть только пара чисел:

Значит, рассмотренная тройка векторов компланарна.
Задание. Располагаются ли в одной плос-ти вектора:

Решение. Нам надо проверить компаланарность векторов, поэтому действуем также, как и в предыдущей задаче. Если вектора компланарны, то существует разложение:

Получилось неверное равенство. Это означает, что у системы уравнений решения нет, и потому тройка векторов некомпланарна.
Скалярное произведение векторов
В 9 классе мы уже изучали скалярное произведение векторов.

Для нахождения угла между векторами необходимо отложить их от одной точки, тогда они образуют такой угол.
Задание. Угол между векторами с и d составляет 60°, а их длины соответственно равны 5 и 6. Найдите их скалярное произведение.
Решение. Здесь для расчета просто перемножаем длины векторов и косинус 60°:

Напомним несколько уже известных нам фактов о скалярном произведении, остающихся верными и в стереометрии:


Формула для расчета скалярного произведения по коорд-там векторов, используемая в стереометрии, несколько отличается от формулы из курса планиметрии. Напомним, что в планиметрии произведение векторов а{xа; уа} и b{хb; yb} можно было рассчитать так:


Задание. Вычислите скалярное произведение векторов:

На практике скалярное произведение обычно используется для расчета углов между векторами, а также отрезками и прямыми. Рассмотрим несколько задач.
Задание. Вычислите угол между векторами:

Теперь через скалярное произведение возможно рассчитать косинус искомого нами угла, а затем и сам угол, который мы обозначим как α:

Задание. Рассчитайте углы в ∆АВС, зная коорд-ты его вершин: А(1; – 1; 3), В(3; – 1; 1) и С(– 1; 1; 3).
Решение. Чтобы найти ∠В, необходимо просто рассчитать угол между векторами ВС и ВА также, как это сделано в предыдущей задаче. Но сначала найдем коорд-ты векторов ВС и ВА и их длины:

Далее рассчитываем скалярное произведение векторов:

Теперь найдем угол А, который представляет собой угол между векторам AВ и AС. Вектор AВ – это вектор, противоположный ВA, то у него та же длина, но противоположный знак у коорд-т:


Задание. В прямоугольном параллелепипеде АВСDA1B1C1D1 ребра имеют длину:
AB = 1
BC = 2
BB1 = 2
Рассчитайте угол между векторами DB1 и BC1.
Решение. Введем систему коорд-т Охуz и расположим в нем параллелепипед следующим образом:

При этом построении граничные точки векторов будут иметь следующие коорд-ты:

Находим коорд-ты векторов, а также их длины:

Рассчитываем скалярное произведение DB1 и BC1:

Получили ноль. Из этого вытекает, что вектора перпендикулярны, то есть искомый нами угол составляет 90°.
Ответ: 90°
Сегодня мы научились использовать координаты для решения стереометрических задач. Почти все формулы, используемые в методе координаты, аналогичны тем формулам, которые были выведены ещё в курсе планиметрии. Надо лишь учитывать существование ещё одной, третьей координаты z.
Простейшие задачи в координатах
Наталья Игоревна Восковская
Эксперт по предмету «Математика»
Задать вопрос автору статьи
К простейшим задачам в координатах относятся следующие задачи:
-
Вычисление координат вектора по координатам его начала и конца.
-
Нахождение координат середины отрезка.
-
Вычисление длины вектора.
-
Вычисление расстояние между двумя точками.
Рассмотрим далее решение этих задач.
Вычисление координат вектора по координатам его начала и конца
Перед тем, как ввести данную задачу напомним понятие радиус вектора данной точки.
Определение 1
Пусть точка $M$ дана в заданной системе координат с началом в точке $O$. Тогда вектор $overrightarrow{OM}$ называется радиус-вектором для точки $M$.
Напомним, что при этом, если $M={x,y}$ в данной системе координат, то вектор $overrightarrow{OM}={x,y}$ в этой системе координат.
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Пример 1
Даны точки $A$ и $B$ имеющие координаты $left{x_1, y_1right}$ и ${x_2, y_2}$ соответственно. Найти координаты вектора $overrightarrow{AB}.$
Решение.
Рассмотрим рисунок по данной задаче (Рис. 1).
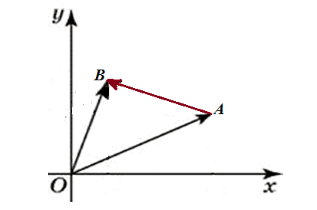
Рисунок 1. Связь между координатами вектора и координатами его начала и конца
По определению разности двух векторов, имеем
[overrightarrow{AB}=overrightarrow{OB}-overrightarrow{OA}]
Следовательно,
[overrightarrow{AB}=left{x_2, y_2right}-left{x_1, y_1right}={x_2-x_1, y_2-y_1}]
Ответ: $overrightarrow{AB}={x_2-x_1, y_2-y_1}$.
Координаты середины отрезка
Пример 2
Даны точки $A$ и $B$ имеющие координаты $left{x_1, y_1right}$ и ${x_2, y_2}$ соответственно. $C$ — середина отрезка $AB$. Найти координаты точки $C.$
Решение.
Обозначим координаты точки $C$ через $left{x, yright}$. Рассмотрим рисунок 2.
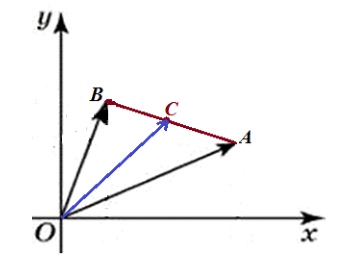
Рисунок 2. Середина отрезка
Из правила параллелограмма, получим
[overrightarrow{OC}=frac{1}{2}(overrightarrow{OA}+overrightarrow{OB})]
Так как векторы $overrightarrow{OC}, overrightarrow{OA} и overrightarrow{OB}$ – радиус-векторы точек $C, A и B$ соответственно, то получим
[overrightarrow{OC}=left{x, yright}, overrightarrow{OA}=left{x_1, y_1right}, overrightarrow{OB}={x_2, y_2}]
Следовательно,
[x=frac{x_1+x_2}{2}, y=frac{y_1+y_2}{2}]
Ответ: $C=left{frac{x_1+x_2}{2}, frac{y_1+y_2}{2}right}$
«Простейшие задачи в координатах» 👇
Вычисление длины вектора по его координатам
Пример 3
Дан вектор $overrightarrow{a}$ с координатами $left{x, yright}$. Найти длину этого вектора.
Решение.
Рассмотрим систему координат $xOy$. Отложим от ее начала координат вектор $overrightarrow{OA}=overrightarrow{a}$. Проведем через точку $A$ перпендикуляры к осям координат $OA_1$ и $OA_2$ (рис. 3).
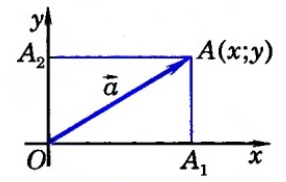
Рисунок 3. Вычисление длины вектора
Так как вектор $overrightarrow{OA}$ – радиус вектор точки $A$, то $A=left{x, yright}$, следовательно,
[OA_1=x, OA_2=y]
Найдем теперь длины вектора по теореме Пифагора:
[{|overrightarrow{a}|}^2={OA_1}^2+{OA_2}^2] [{|overrightarrow{a}|}^2=x^2+y^2] [left|overrightarrow{a}right|=sqrt{x^2+y^2}]
Ответ: $sqrt{x^2+y^2}$.
Расстояние между двумя точками
Пример 4
Даны точки $A$ и $B$ имеющие координаты $left{x_1, y_1right}$ и ${x_2, y_2}$ соответственно.Найти $d$ — расстояние между точками $A$ и $B$ через их координаты.
Решение.
Рассмотрим рисунок 4.
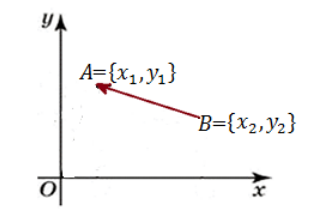
Рисунок 4. Расстояние между точками
[ d=|overrightarrow{AB}|]
Используя задачу 1, получим, что вектор $overrightarrow{AB}$ имеет координаты
[overrightarrow{AB}={x_2-x_1, y_2-y_1}]
Найдем длину данного вектора. По задаче 3, имеем
[d=left|overrightarrow{AB}right|=sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2}]
Ответ: $d=sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 05.04.2023

