В решении задач данного типа мы используем понятие “векторного произведение двух векторов”.
Векторным произведением двух векторов a и b называют такой вектор с, который перпендикулярен плоскости, построенных на векторах a и b и его длина равна площади параллелограмма, построенных на векторах a и b.
Алгоритм решения данной задачи.
1. Вводим систему координат ОXYZ.
2. Найдём координаты нужных точек: A(x1;y1;z1), B(x2;y2;z2), M0(x0;y0;z0).
3. Напишем уравнение прямой AB.
4. Найдем координаты направляющего вектора прямой AB.
5. Найдем длину направляющего вектора.
6. Найдем координаты вектора AB.
8. Найдём координаты вектора – связи например, МА.
9. Найдём векторное произведение векторов AB и AM.
10. Найдем расстояние от точки M до прямой AB по формуле:
11. Записываем ответ.
Видеоразбор задачи
Интерактивное приложение с задачами данного вида:
Задание №1
Задание №2
Задание №3
Задание №4
Задание №5
Буду рада вам! Подписывайтесь!
https://www.youtube.com/channel/UCrrze24VyUrfKKfpoa9uL1Q
Расстояние d между точками в пространстве A11;y1;z1>, A22;y2;z2> представляется формулой
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.3 / 5. Количество оценок: 8
Оценок пока нет. Поставьте оценку первым.
3 комментария
найти расстояние между точками с(-2;1;-2) д (-1;2;1) м (-1;0;2) н (1;-1;2) найти 3 вектора сд — 2 вектора мн
Как найти расстояние через вектор
- +7 (953) 35-222-89
- Санкт-Петербург, Лиговский пр.52
- Kyziaha@gmail.com
Метод координат (расстояние между точкой и плоскостью, между прямыми)
Расстояние между точкой и плоскостью.
Расстояние между точкой и прямой.
Расстояние между двумя прямыми.
Первое, что полезно знать, это как найти расстояние от точки до плоскости:
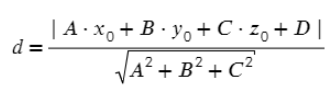
Значения A, B, C, D – коэффициенты плоскости
x, y, z – координаты точки
Задача. Найти расстояние между точкой А = (3; 7; −2) и плоскостью 4x + 3y + 13z – 20 = 0.
Все дано, можно сразу подставить значения в уравнение:
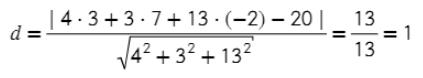
Задача. Найдите расстояние от точки К = (1; −2; 7) до прямой, проходящей через точки V = (8; 6; −13) и T = (−1; −6; 7).
- Находим вектор прямой.
- Вычисляем вектор, проходящий через искомую точку и любую точку на прямой.
- Задаем матрицу и находим определитель по двум полученным векторам в 1-ом и 2-ом пункте.
- Расстояние получим, когда квадратный корень из суммы квадратов коэффициентов матрицы поделим на длину вектора, который задает прямую (Думаю непонятно, поэтому перейдем к конкретному примеру).
1) TV = (8−(−1); 6−(−6); -13-7) = (9; 12; −20)
2) Вектор найдем через точки K и T, хотя так же можно было бы через K и V или любую другую точку на данной прямой.
TK = (1−(−1); −2−(−6); 7-7) = (2; 4; 0)
3) П олучится м атрица без коэффициента D (здесь он не нужен для решения):
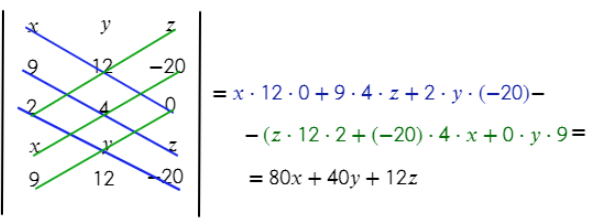Если непонятно, как получить матрицу и ее определитель, смотрите здесь более подробный разбор.
4) Плоскость получилась с коэффициентами А = 80, В = 40, С = 12,
x, y, z – координаты вектора прямой, в данном случае – вектор TV имеет координаты (9; 12; −20)
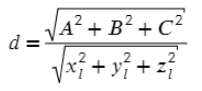
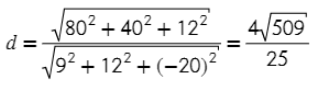
Задача. Найти расстояние между прямой, проходящей через точки Е = (1; 0; −2), G = (2; 2; −1), и прямой, проходящей через точки M = (4; −1; 4), L = (−2; 3; 0).
- Задаем векторы обеих прямых.
- Находим вектор, взяв по одной точке с каждой прямой.
- Записываем матрицу из 3-х векторов (две строчки из 1-го пункта, одна строчка из 2-го) и находим ее численный определитель.
- Задаем матрицу из двух первых векторов (в пункте 1). Первую строчку задаем как x, y, z.
- Расстояние получим, когда разделим получившееся значение из пункта 3 по модулю на квадратный корень из суммы квадратов пункта 4.
Перейдем к цифрам:
1) EG = (2−1; 2−0; −1−2) = (1; 2; −3)
ML = (−2−4; 3−(−1); 0−4) = (−6; 4; −4)
2) Найдем вектор EM (можно было так же найти EL или GM, или GL).
EM = (1−4; 0−(−1); −2−4) = (−3; 1; −6)
3) Составляем матрицу из трех выше найденных векторов и находим определитель. 
4) Составляем матрицу из первых двух выше найденных векторов и находим определитель
без коэффициента D (здесь он не нужен для решения).
Вспомним, что уравнение плоскости задается так: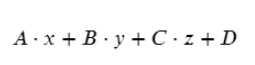
В нашем случае А = 4, В = 22, С = 16, D = 0.
5) Итоговая формула выглядит так, где L= −86 (из 3 пункта)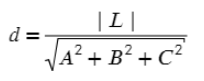
Векторы в пространстве и метод координат
Существует два способа решения задач по стереометрии
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
Система координат в пространстве
Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.
Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.
Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами и :
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.
Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму:
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.
Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов и , а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
То есть A + C + D = 0.
Аналогично для точки K:
Получили систему из трех уравнений:
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
Выразим C и B через A и подставим в третье уравнение:
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.
Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂
Строим чертеж. Прямую четырехугольную призму можно по-другому назвать “параллелепипед”.
Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор .
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Получим:
Ответ:
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.
Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.
Находим синус угла между прямой m и плоскостью α по формуле:
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат
Находим координаты вектора .
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Ответ:
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA1 = . Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:
Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему. Выберем
Тогда
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
[spoiler title=”источники:”]
http://ik-study.ru/ege_math/zagholovok_stat_i0
http://ege-study.ru/ru/ege/materialy/matematika/vektory-v-prostranstve-i-metod-koordinat/
[/spoiler]
МКУ «Районное управление образования»
Администрация МО «Кабанский район»
МАОУ «Селенгинаская гимназия»
Секция «Математика»
Решение стереометрических задач на вычисление
расстояний векторным методом
Автор Лукьянов Родион Сергеевич,
ученик 10 А класса.
Научный руководитель
Фаркова Мария Николаевна, учитель
математики
МАОУ «Селенгинская гимназия».
2021
Содержание
|
Введение |
2 |
|
1. Векторный метод решения стереометрических |
3 |
|
2. Типы геометрических задач и схемы их решения |
4 |
|
3. Апробация |
9 |
|
Заключение |
10 |
|
Список литературы |
11 |
|
Приложение 1 |
12 |
|
Приложение 2 |
13 |
|
Приложение 3 |
16 |
|
Приложение 4 |
18 |
Введение
В своей деятельности человеку повсюду
приходится сталкиваться с необходимостью, изучать форму, размеры, взаимное
расположение пространственных фигур. Подобные задачи решают и астрономы,
имеющие дело с самыми большими масштабами, и физики, исследующие структуру
атомов и молекул. Раздел геометрии, в котором изучаются такие задачи,
называется стереометрией.
Участвуя в различных математически
конкурсах, олимпиадах, а так же в ходе подготовки к ЕГЭ я часто сталкиваюсь со
стереометрическими задачами на нахождение расстояний между точками, прямыми и
плоскостями.
Решая их комбинированным методом, который чаще всего
применяется при решении задач на уроках геометрии, у меня возникают трудности,
связанные с дополнительными построениями и необходимыми обоснованиями, сопровождающими
эти построения. Я
не всегда уверен в полученном ответе, поэтому возникает необходимость выполнить
проверку, решив данную задачу другим способом.
И для этого я решил познакомиться с
другими способами решения стереометрических задач. Мое внимание привлек
векторный метод,
так при использовании данного метода не требуется дополнительное исследование
решения и рассмотрение частных случаев. Решение задач с использованием векторов
позволяет сохранить геометрическую наглядность, но в тоже время не требует
проведения дополнительных линий. Это и доказывает актуальность выбранной и рассматриваемой
мной темы.
Объект
исследования: стереометрические задачи на вычисление
расстояний.
Предмет
исследования: решение задач
на вычисление расстояний векторным
методом.
Цель исследования: изучить
векторный метод и научиться его применять при решении стереометрических задач
на нахождение расстояний
Гипотеза: применение
векторного метода при решении стереометрических задач на вычисление расстояний
упрощает их решение.
Для достижения поставленной цели исследования и проверки
достоверности сформулированной гипотезы необходимо решить следующие задачи:
1. Рассмотреть типы стереометрических задач на вычисление
расстояний;
2. Изучить схемы решения задач векторным способом;
3. Сравнить решение задач векторным и комбинированным способом;
4. Подобрать задачный материал;
5. Создать методические рекомендации для учащихся.
Методы исследования:
1.Сравнительно-сопоставительный анализ математической и учебной
литературы;
2. Конструирование заданий;
3. Систематизация способов решения;
4. Качественный и количественный анализ результатов.
1. Векторный метод решения
стереометрических задач
Векторный метод является
одним из методов, позволяющих геометрические задачи решать средствами алгебры.
Поэтому, при использовании векторного метода не требуется дополнительное
исследование решения и рассмотрение частных случаев, что нередко приходится
делать при решении задач другими методами. Т.е одно из достоинств метода его
общность. Решение задачи с использованием векторов позволяет сохранить
геометрическую наглядность, но в тоже время не требует проведения
дополнительных линий.
Основная идея метода (в геометрии):
геометрические задачи решаются аналитическим способом за счет «перевода» задачи
на векторный язык и использовании средств векторной алгебры.
Обьективная сторона метода (т.е
совокупность основных понятий): вектор, начало вектора, конец вектора, модуль
вектора, угол между векторами, скалярное произведение векторов, единичный
вектор, свойства векторов, определения операций над векторами и их свойства,
соотношения между векторами (равенство, коллинеарность, комплонарность и т.д) и
другие положения.
Для решения задач необходимо уметь
выражать геометрические факты в виде соотношений между векторами, а также
выполнять следующие действия по реализации метода:
1. Осуществлять переход от
соотношений между фигурами к соотношению между векторами.
2. Выполнять операции над векторами,
представлять вектор в виде суммы, разности, произведения вектора на число.
3. Правильно выбирать базисные
векторы.
4. Находить скалярное произведение
векторов.
5. Разлагать вектор по базисным
векторам.
6. Находить отношения между
векторами.
7. Находить длину вектора, угол между
двумя векторами.
8. Преобразовывать векторные
соотношения, осуществлять переход от соотношения между векторами к соотношению
между длинами и наоборот.
9. Выражать длину вектора через его
скалярный квадрат, выражать величину угла между векторами через их скалярное
произведение.
10. Доказывать коллинеарность и
комплонарность векторов.
11. Доказывать равенство векторов.
Признак выбора метода
Стереометрическую задачу
можно решить векторным методом, если в ней:
1. Можно удобно расположить
базисные векторы, т.е известны углы между сторонами фигуры, либо их можно
найти;
2. Известны длины сторон,
которые можно выбрать за базисные векторы или отношение между ними (либо их
можно легко выразить через другие стороны);
При применении векторного
метода имеет место «перевод» задачи на язык векторов и обратный переход от
векторов к терминам исходной задачи. Поэтому авторы многих работ посвященных
векторному методу, рекомендуют составление специального «словаря» для перехода
от математического языка к векторному и обратно.
Этот «словарь» можно
представить в виде таблицы. (Приложение 1)
2.
Типы задач и схемы их решения
В ходе исследования, мною были
рассмотрены задачи на вычисление расстояний, которые я распределил на 4 типа:
·
Расстояние
между двумя точками.
·
Расстояние
от точки до прямой.
·
Расстояние
от точки до плоскости.
·
Расстояние
между скрещивающимися прямыми.
Рассмотрим схемы решения для
каждого типа задач.
1) Расстояние между точками
Пусть даны две точки
пространства 
и 
.
Расстояние между точками можно вычислить по следующей схеме:
1. Выбираем тройку базисных
векторов (в качестве базисных векторов выбирают те векторы, если известны их
длины и углы между ними, или их можно вычислить).
2. Составляем таблицу
умножения векторов базиса.
Пусть 
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Выразим
векторы 
через базисные векторы
, где 
– коэффициенты разложения.
4. Выразим длину вектора
через его скалярный квадрат 
, позволяющий вычислить искомую величину.
Пример 1: В треугольной пирамиде 
известны длины ребер 
, 
и углы 
. Точки 
– середины ребер 
и 
соответственно, точка 
– точка пересечения медиан
треугольника 
. Вычислите: а) расстояние между точками 
и 
; б) длину отрезка 
; в) длину отрезка 
. Решение данной задачи представлено
в Приложении 2.
2. Расстояние от точки до
прямой
Определение 1: Расстоянием от точки до
прямой, не
содержащей эту точку называется длина отрезка перпендикуляра, проведенного из
этой точки на прямую.
Пусть
дана прямая 
и точка 
(рис. 1).
Расстояние от точки до прямой можно вычислить по следующей схеме:
1.
Выбираем
тройку базисных векторов: 
.
2. Составляем таблицу
умножения векторов базиса.
3.
Выразим вектор 
через базисные векторы. рис. 1
4. Пусть 
, где 
. Выразим 
через базисные векторы.
Так как 
коллинеарен , то 
, получаем 
.
5. Составляем уравнение для
нахождения коэффициентов разложения вектора 
по базисным векторам. Так как , то 
.
Учитывая, таблицу умножения
векторов базиса данное уравнение позволяет найти значение 
.
6. Расписываем разложение
вектора 
, подставив полученное значение в разложение
7. Выразим длину вектора
через его скалярный квадрат 
, позволяющий вычислить искомую величину.
Пример 2: В правильной треугольной
призме
, все ребра которой равны 1. Найдите
расстояние от точки до прямой 
. Решение данной задачи представлено в Приложении
2.
3. Расстояние от точки до
плоскости
Определение 2: Расстоянием от точки до плоскости, не содержащей эту точку,
называется длина отрезка перпендикуляра, опущенного из этой точки на плоскость.
Пусть дана плоскость 
и точка 
(рис. 2)
. Расстояние от точки до плоскости можно вычислить по следующей схеме:
1. Выбираем
тройку базисных векторов: 
.
2. Составляем таблицу
умножения векторов базиса. рис. 2
3. Выразим вектор 
и 
через базисные векторы, (
и 
неколлинеарные)
4. Пусть 
, где 
. Выразим 
через
базисные векторы: 
. Учитывая что 
, получаем 
5. Составляем систему
уравнений для нахождения коэффициентов разложения вектора 
по базисным векторам.
Учитывая, таблицу умножения
векторов базиса находим значение 
и 
.
6. Расписываем разложение
вектора , подставив полученные значения х и y в 
.
7. Выразим длину вектора
через скалярный квадрат , позволяющий вычислить искомую величину.
Пример 3: В правильной треугольной
призме 
стороны основания равны 2, точка 
– середина ребра 
.
Найти расстояние от вершины 
до плоскости 
, если 
Решение: (рис. 3)
1. Выбираем тройку базисных
векторов: 
.
2. Составляем таблицу
умножения векторов базиса:
3. Выразим вектор 
и 
через базисные векторы
4. Пусть 
, где 
.
Выразим 
через базисные векторы:
, учитывая что 
,
получаем:
.
рис.3
5. Составляем систему
уравнений для нахождения коэффициентов разложения вектора 
по базисным векторам
Учитывая, таблицу умножения
векторов базиса получаем 
6. Расписываем разложение
вектора: 
7. Выражаем длину вектора
через скалярный квадрат 
, позволяющий вычислить искомую величину. 
.
Ответ: 
.
Так же я решил данную задачу комбинированным
методом.
Комбинированный метод
позволяет решить задачу применяя геометрический и алгебраический метод
одновременно. Часто
при решении конкретной задачи, нет необходимости применять до конца какой-либо метод
в «чистом виде». На каком-то этапе решения может быть применен, например,
поэтапно – вычислительный метод, после чего составляется уравнение, например
методом опорного элемента, и наконец, геометрическим методом доказывается
некоторое требуемое утверждение.
Решение: (рис. 4)
Пусть прямая 
пересекает прямую 
в
точке 
. Тогда плоскости 
и
пересекаются по прямой 
. Из точки 
опустим
перпендикуляр 
на прямую , тогда отрезок 
(проекция
) перпендикулярен .
Прямая 
. Высота 
треугольника
перпендикулярна плоскости 
– расстояние от точки 
до плоскости 
.
рис.4
Так как точка – середина ребра 
,
то 
. Из равенства прямоугольных треугольников
и 
(
) получаем 
.
Следовательно, 
– равнобедренный в нем 
, 
,
высота является биссектрисой 
.
В прямоугольном треугольнике с прямым углом С: 
.
Ответ: 
.
При решении данной задачи комбинированным
методом мне необходимо было знать: признак перпендикулярности прямой и
плоскости; теорему о трех перпендикулярах; признак перпендикулярности
плоскостей; признаки равенства треугольников; определение равнобедренного
треугольника; свойство смежных углов; метрические соотношения в прямоугольном
треугольнике; теорему Пифагора; метод следов.
А так же уметь: применять
перечисленные знания при решении задач; выполнять построение чертежа и
сведение задачи к планиметрической.
При решении
задачи векторным методом необходимо было воспользоваться свойством
скалярного произведения. А так же уметь: выбирать тройку базисных векторов;
составлять
таблицу умножения векторов базиса; выполнять разложение вектора по базисным
векторам; составлять систему уравнений для нахождения коэффициентов
разложения вектора по базисным векторам; выражать длину вектора через
скалярный квадрат.
Таким образом, можно сделать вывод:
при решении данной задачи (которая является задачей из ЕГЭ) комбинированный метод требует от учащихся
развитого пространственного воображения, отличного знания аксиом и теорем
стереометрии, умение построить чертеж, так как построение перпендикуляра
требует выхода за рамки фигуры, чего большинство учащихся не видит, а для
векторного метода не обязательно знать как расположен данный перпендикуляр,
нужно лишь определить тип задачи и применить соответсвующую схему решения.
4. Расстояние между
скрещивающимися прямыми
Определение 3: Расстоянием между двумя
скрещивающимися прямыми называется длина отрезка их общего перпендикуляра.
Схема решения задач данного
типа представлена в Приложении 3.
Все схемы решения задач для
наглядности я представил в виде таблицы. (Приложение 4)
3. Апробация
Изучив
схемы решения стереометрических задач векторным методом, я решил поделиться
полученными знаниями со своими одноклассниками. Но перед этим я предложил им
решить 3 задачи известным им способом. Результаты получились следующие:
|
Количество верно решенных задач |
Количество человек |
|
3 |
1 |
|
2 |
4 |
|
1 |
4 |
|
0 |
1 |
После
чего я провел для своих одноклассников 8 занятий по решению стереометрических задач
векторным методом.
На последнем занятии провел небольшую
самостоятельную работу, чтобы выявить эффективность применения векторного метода
при решении стереометрических задач на вычисление расстояний.
Результаты я представил в виде таблицы:
|
Фамилия, имя ученика |
Число правильно решенных задач |
||
|
1 |
2 |
3 |
|
|
Буянов Кирилл |
+ |
+ |
|
|
Гурулев Артем |
+ |
+ |
+ |
|
Дунаев Влад |
+ |
|
+ |
|
Захаров Никита |
+ |
+ |
+ |
|
Кокин Артем |
+ |
+ |
+ |
|
Кутырев Артем |
+ |
+ |
+ |
|
Мелентьев Илья |
+ |
+ |
+ |
|
Токмаков Сергей |
+ |
|
+ |
|
Ульянов Владимир |
+ |
|
|
|
Фоминых Павел |
+ |
+ |
|
Обозначения в таблице: «+» – задача решена в полной мере, описаны все
этапы решения; «
» – в решении были допущены
некоторые ошибки (вычислительные, нет описания этапов решения).
Данные представленной таблицы для наглядности я
отразил с помощью диаграммы, для удобства обозначим «+» – 1балл, «» – 0,5 балла.
На основании,
полученных результатов, можно сделать вывод, что решение задач векторным методом не
вызывают затруднений у моих одноклассников, а значит данный метод действительно
позволяет решать стереометрические задачи на вычисление расстояний намного
быстрее и качественнее.
Заключение
В
процессе написания данной работы, поставленная цель достигнута, следующие
задачи исследования разрешены:
1. Подобран и систематизирован
теоретический материал, необходимый для изучения темы «Решение
стереометрических задач на вычисление расстояний векторным методом»;
2. Изучены схемы решения задач;
3. Подобран задачный материал;
4. Проведено сравнение решения задач
векторным и комбинированным способом;
5. Разработаны методические рекомендации для учащихся.
6. Проведены занятия для учащихся 10 А класса с целью
подтверждения сформулированной гипотезы.
Список литературы
1. Александров А. Д. Геометрия для 10-11кл: учебное пособие
для учащихся школ и классов с углубленным изучением математики/ А. Д.
Александров, А. Л. Вернер, В.И. Рыжиков. – 5-е изд. – М.: Просвещение, 2007.-464с.
2. Атанасян Л.С. Курс элементарной геометрии. Часть- 2
(стереометрия)/ Л.С. Атанасян, Н. С Денисова, Е.В. Силаев. – М.: Синтакс –
экспресс, 2006-287с.
3. Готман Э.Г. Стереометрические задачи и методы их
решения. Э. Г. Готман. – М.:МЦНМО, 2006. – 160 с.
4. Плакатина О. И. Специальная методика преподавания
математики в средней школе: Учеб. пособие по теории и методике обучения
математике для студентов педагогических вузов специальности 032100-математика/
О. И. Плакатина –Иркутск, 2004-268с.
5. Потоскуев Е.В. Геометрия. 11кл.: учеб. для общеобразовательных
учреждений с углубленным и профильным изучением математики/ Е.В. Потоскуев. –
М.: Дрофа, 2006-368с.
6. Федин, Н.Г. Геометрия: Учебное пособие для техникумов/
Н. Г. Федин, С. Н. Федин. – М.: Высшая школа, 2001.-350с.
7. Шестаков, С.А. Векторы на экзаменах. Векторный метод в
стереометрии/ С. А. Шестаков. – М.: МЦНМО, 2005.-112с.
Приложение 1
Таблица перехода от математического
языка к векторному
|
Язык геометрии |
Язык векторов |
|
|
|
|
|
|
|
Точка С принадлежит |
|
|
М-середина отрезка АВ |
|
|
Прямые АВ, СD, МК принадлежат одной |
|
|
|
|
|
М – центроид треугольника АВС |
|
|
Точка С – делит |
|
|
О, А, В, С – |
|
|
АВСD – параллелограмм |
|
|
|
|
Приложение 2
Примеры решения задач векторным методом
Пример 1: В треугольной пирамиде 
известны длины ребер 
, 
и углы 
. Точки 
– середины ребер 
и 
соответственно, точка 
– точка пересечения медиан
треугольника 
. Вычислите:
а) расстояние между точками 
и 
;
б) длину отрезка 
;
в) длину отрезка 
.
Решение: (рис. 1)
рис. 1
1. Выбираем тройку базисных
векторов: 
.
2. Составляем таблицу
умножения векторов базиса:
|
|
|
|
|
|
|
1 |
1 |
0 |
|
|
1 |
4 |
4 |
|
|
0 |
4 |
16 |
3. Выразим векторы 
через базисные векторы
.
.
4. Выразим длину вектора
через его скалярный квадрат 
, позволяющий вычислить искомую величину.
Ответ: 
.
Пример 3: В правильной треугольной
призме
, все ребра которой равны 1. Найдите
расстояние от точки до прямой 
.
Решение: (рис. 2)
рис. 2
1. Выбираем тройку базисных
векторов: 
.
2. Составляем таблицу
умножения векторов базиса:
|
|
|
|
|
|
|
1 |
|
0 |
|
|
|
1 |
0 |
|
|
0 |
0 |
1 |
3. Выразим вектор 
через базисные векторы
.
4. Пусть 
, где 
Выразим 
через базисные векторы: 
.
Учитывая что 
, получаем 
.
5. Составляем уравнение для
нахождения коэффициентов разложения вектора 
по базисным векторам.
. Учитывая, таблицу умножения
векторов базиса получаем 
.
6. Расписываем разложение
вектора 
.
7. Выразим длину вектора
через его скалярный квадрат 
, позволяющий вычислить искомую величину.
Ответ: 
.
Приложение 3
Расстояние между скрещивающимися прямыми
Пусть
даны скрещивающиеся прямые 
и 
. Расстояние между скрещивающимися
прямыми можно вычислить по следующей схеме:
1. Выбираем тройку базисных
векторов: 
.
2. Составляем таблицу умножения векторов базиса.
3. Выразим 
и 
через базисные векторы.
4. Пусть 
, где 
. Выразим 
через базисные векторы: 
, где 
.
Учитывая, что 
, получаем 
.
5. Составляем систему
уравнений для нахождения коэффициентов разложения вектора по базисным векторам.
Учитывая, таблицу умножения
векторов базиса получаем значение 
и 
.
6. Расписываем разложение
вектора , подставив полученные значения и в 
.
7. Выразим длину вектора
через скалярный квадрат 
, позволяющий вычислить искомую величину.
Пример 4: В треугольной пирамиде известны длины ребер 
и углы 
. На
ребре 
взята точка так,
что 
. Найдите расстояние между прямыми 
и 
.
Решение:
1. Выбираем тройку базисных
векторов: 
.
2. Составляем таблицу умножения
векторов базиса:
|
|
|
|
|
|
|
1 |
0 |
-1 |
|
|
0 |
4 |
2 |
|
|
-1 |
2 |
4 |
3. Выразим 
и 
через базисные векторы
4. Пусть 
, где 
Выразим 
через базисные векторы: 
Учитывая что 
, получаем
5. Составляем систему
уравнений для нахождения коэффициентов разложения вектора по базисным векторам.
Учитывая, таблицу умножения
векторов базиса получаем
6. Расписываем разложение вектора. 
.
7. Выразим длину вектора
через скалярный кввадрат 
, позволяющий вычислить искомую величину.
.
Ответ: 
.
Приложение
4
Схемы
решения стереометрических задач на вычисление расстояний
векторным
методом
|
Расстояние
|
Расстояние от |
Расстояние от |
Расстояние |
|
1. Выбираем тройку |
1. Выбираем тройку |
1. Выбираем тройку |
1. Выбираем тройку |
|
2. Составляем таблицу |
2. Составляем таблицу |
2. Составляем таблицу |
2. Составляем таблицу |
|
3. Выразим векторы |
3. Выразим вектор |
3. Выразим вектор |
3. Выразим |
|
4. Выразим длину |
4. Пусть |
4. Пусть Выразим |
4. Пусть Выразим |
|
5. Составляем |
5. Составляем систему |
5. Составляем систему |
|
|
6. Расписываем |
6. Расписываем |
6. Расписываем |
|
|
7. Выразим длину |
7. Выразим длину |
7. Выразим длину |
Нахождение кратчайшего расстояния между прямыми в пространстве
Содержание:
- Что такое расстояние между прямыми в пространстве
- Метод координат для определения расстояния
-
Примеры задач с решением
- Задача 1
- Задача 2
Что такое расстояние между прямыми в пространстве
Для начала дадим определение этому понятию.
Определение
Расстояние между прямыми в пространстве — это отрезок, который соединяет две прямые линии по самому короткому пути. Иными словами, он перпендикулярен обеим этим прямым.
Но не всегда две линии могут быть параллельны друг другу.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Определение
Расстояние между двумя скрещивающимися прямыми в пространстве — это расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через вторую прямую параллельно первой.
Таким образом, чтобы найти расстояние между этими скрещивающимися прямыми, нужно от одной из прямых провести перпендикуляр на плоскость, в которой лежит другая прямая.
Между параллельными прямыми расстояние одинаково на протяжении всей их длины: перпендикуляр, опущенный из любой точки одной из этих линий, всегда будет одной и той же величины.
Метод координат для определения расстояния
Разберем пошагово способ определения расстояния между двумя скрещивающимися прямыми с помощью метода координат.
- Определить координаты точек (М_1) и (М_2), лежащих соответственно на прямых a и b.
- Найти x, y и z направляющих векторов для прямых a и b.
- Найти вектор-нормаль для плоскости, в которой лежит прямая b с помощью векторного произведения (overrightarrow a) и (overrightarrow b).
- Записать общее уравнение плоскости: (A(x-x_0)+B(y-y_0)+C(z-z_0)=0) и потом записать к нормированному виду уравнения плоскости, которое выглядит так: (xtimescosleft(alpharight)+ytimescosleft(betaright)+ztimescosleft(gammaright)-p=0), где p — свободный член (число, которое равно расстоянию точки начала координат до плоскости), а (cosleft(alpharight),;cosleft(betaright)) и (cosleft(gammaright)) — координаты единичного нормального вектора плоскости.
- Далее, для определения расстояния от точки M до искомой плоскости, воспользуемся следующим уравнением: (M_1H_1=left|x_1timescosleft(alpharight)+y_1timescosleft(betaright)+z_1cosleft(gammaright)-pright|), где (x_1), (y_1) и (z_1) — координаты точки (M_1), лежащей на прямой a, а (H_1) — точка, лежащая на искомой плоскости.
Примеры задач с решением
Задача 1
Дан куб (ABCDA_1B_1C_1D_1) с ребром равным (sqrt{32}) см. Найти расстояние между прямыми (DB_1) и (CC_1).
Решение
Расстояние между скрещивающимися прямыми будем искать в качестве расстояния между прямой (CC_1) и плоскостью, проходящей через (DB_1) параллельно (CC_1). Так как (DD_1parallel CC_1), плоскость ((B_1D_1D)) параллельна (СС_1).
Сначала нужно доказать, что (CO) — перпендикуляр, проведенный к этой плоскости. (COperp BD) (как диагонали квадрата) и (COperp DD_1) (так как ребро (DD_1) перпендикулярно всей плоскости ((ABC))). Получается, (CO) перпендикулярен двум пересекающимся прямым из плоскости. Значит, (COperp(B_1D_1D)).
(AC) — диагонально квадрата — равна (ABsqrt2), то есть (AC=sqrt{32}timessqrt2=sqrt{64}=8) см. Следовательно, (CO=frac12times AC=4) см.
Ответ: 4 см.
Задача 2
В трехмерном пространстве в прямоугольной системе координат Oxyz заданы две скрещивающиеся прямые a и b. Прямую a определяют параметрические уравнения прямой в пространстве:
(left{begin{array}{l}x=-2\y=1+2timeslambda\z=4-3timeslambdaend{array}right.)
А прямую b канонические уравнения прямой в пространстве:
(frac x1=frac{y-1}{-2}=frac{z+4}6).
Вычислить расстояние между заданными прямыми.
Решение
Прямая a проходит через точку (M_1(-2, 1, 4)) и имеет направляющий вектор (overrightarrow a=(0, 2, -3)). Прямая b проходит через точку (M_2 (0, 1, -4)), а ее направляющий вектором является вектор (overrightarrow b=(1, -2, 6)).
Найдем векторное произведение векторов( overrightarrow a=(0, 2, -3)) и (overrightarrow b=(1, -2, 6): left[overrightarrow atimesoverrightarrow bright]=begin{vmatrix}overrightarrow i&overrightarrow j&overrightarrow k\0&2&-3\1&-2&6end{vmatrix}=6timesoverrightarrow i-3timesoverrightarrow j-2timesoverrightarrow k).
Так, (overrightarrow n=left[overrightarrow atimesoverrightarrow bright]) плоскости X, проходящей через прямую b параллельно прямой a, имеет координаты (6, -3, -2).
Таким образом, уравнение плоскости X есть уравнение плоскости, проходящей через точку (M_2(0, 1, -4)) и имеющей нормальный вектор (overrightarrow n=(6, -3, -2)):
(6times(x-0)-3times(y-1)-2times(z-(-4))=0;leftrightarrow6x-3y-2z-5=0)
Нормирующий множитель для общего уравнения плоскости (6x-3y-2z-5=0) равен (frac1{sqrt{6^2+{(-3)}^2+{(-2)}^2}}=frac17). Значит, нормальное уравнение этой плоскости выглядит как (frac67x-frac37y-frac27z-frac57=0).
Воспользуемся формулой для вычисления расстояния от точки (M_1(-2, 1, 4)) до плоскости (frac67x-frac37y-frac27z-frac57=0: left|M_1H_1right|=left|frac67times(-2)-frac37times1-frac27times4-frac57right|=left|frac{-28}7right|=4) см.
Ответ: 4 см.
Содержание
- Расстояние от точки до плоскости: определение и примеры нахождения
- Расстояние от точки до плоскости – определение
- Расстояние от точки до плоскости – теория, примеры, решения
- Расстояние от точки до плоскости (ЕГЭ 2022)
- Расстояние от точки до плоскости — коротко о главном
- Расстояние от точки до плоскости
- Способы нахождения расстояния от точки до плоскости
- Геометрический способ
Расстояние от точки до плоскости: определение и примеры нахождения
Данная статья рассказывает об определении расстояния от точки до плоскости. произведем разбор методом координат, который позволит находить расстояние от заданной точки трехмерного пространства. Для закрепления рассмотрим примеры нескольких задач.
Расстояние от точки до плоскости – определение
Расстояние от точки до плоскости находится посредством известного расстояния от точки до точки, где одна из них заданная, а другая – проекция на заданную плоскость.
Когда в пространстве задается точка М 1 с плоскостью χ , то через точку можно провести перпендикулярную плоскости прямую. Н 1 является общей точкой их пересечения. Отсюда получаем, что отрезок М 1 Н 1 – это перпендикуляр, который провели из точки М 1 к плоскости χ , где точка Н 1 – основание перпендикуляра.
Расстоянием от точки до плоскости называют расстояние от заданной точки к основанию перпендикуляра, который провели из заданной точки к заданной плоскости.
Определение может быть записано разными формулировками.
Расстоянием от точки до плоскости называют длину перпендикуляра, который провели из заданной точки к заданной плоскости.
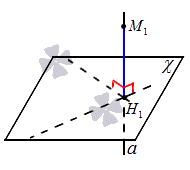
Расстояние от точки М 1 к плоскости χ определяется так: расстояние от точки М 1 до плоскости χ будет являться наименьшим от заданной точки до любой точки плоскости. Если точка Н 2 располагается в плоскости χ и не равна точке Н 2 , тогда получаем прямоугольный треугольник вида М 2 H 1 H 2 , который является прямоугольным, где имеется катет М 2 H 1 , М 2 H 2 – гипотенуза. Значит, отсюда следует, что M 1 H 1 M 1 H 2 . Тогда отрезок М 2 H 1 считается наклонной, которая проводится из точки М 1 до плоскости χ . Мы имеем, что перпендикуляр, проведенный из заданной точки к плоскости, меньше наклонной, которую проводят из точки к заданной плоскости. Рассмотрим этот случай на рисунке, приведенном ниже.
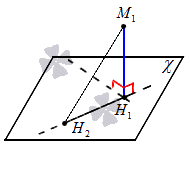
Расстояние от точки до плоскости – теория, примеры, решения
Существует ряд геометрических задач, решения которых должны содержать расстояние от точки до плоскости. Способы выявления этого могут быть разными. Для разрешения применяют теорему Пифагора или подобия треугольников. Когда по условию необходимо рассчитать расстояние от точки до плоскости, заданные в прямоугольной системе координат трехмерного пространства, решают методом координат. Данный пункт рассматривает этот метод.
По условию задачи имеем, что задана точка трехмерного пространства с координатами M 1 ( x 1 , y 1 , z 1 ) с плоскостью χ , необходимо определить расстояние от М 1 к плоскости χ . Для решения применяется несколько способов решения.
Первый способ
Данный способ основывается на нахождении расстояния от точки до плоскости при помощи координат точки Н 1 , которые являются основанием перпендикуляра из точки М 1 к плоскости χ . Далее необходимо вычислить расстояние между М 1 и Н 1 .
Для решения задачи вторым способом применяют нормальное уравнение заданной плоскости.
Второй способ
По условию имеем, что Н 1 является основанием перпендикуляра, который опустили из точки М 1 на плоскость χ . Тогда определяем координаты ( x 2 , y 2 , z 2 ) точки Н 1 . Искомое расстояние от М 1 к плоскости χ находится по формуле M 1 H 1 = ( x 2 — x 1 ) 2 + ( y 2 — y 1 ) 2 + ( z 2 — z 1 ) 2 , где M 1 ( x 1 , y 1 , z 1 ) и H 1 ( x 2 , y 2 , z 2 ) . Для решения необходимо узнать координаты точки Н 1 .
Имеем, что Н 1 является точкой пересечения плоскости χ с прямой a , которая проходит через точку М 1 , расположенную перпендикулярно плоскости χ . Отсюда следует, что необходимо составление уравнения прямой, проходящей через заданную точку перпендикулярно к заданной плоскости. Именно тогда сможем определить координаты точки Н 1 . Необходимо произвести вычисление координат точки пересечения прямой и плоскости.
Алгоритм нахождения расстояния от точки с координатами M 1 ( x 1 , y 1 , z 1 ) к плоскости χ :
- составить уравнение прямой а, проходящей через точку М 1 и одновременно
- перпендикулярной к плоскости χ ;
- найти и вычислить координаты ( x 2 , y 2 , z 2 ) точки Н 1 , являющимися точками
- пересечения прямой a с плоскостью χ ;
- вычислить расстояние от М 1 до χ , используя формулу M 1 H 1 = ( x 2 — x 1 ) 2 + ( y 2 — y 1 ) 2 + z 2 — z 1 2 .
В заданной прямоугольной системе координат О х у z имеется плоскость χ , тогда получаем нормальное уравнение плоскости вида cos α · x + cos β · y + cos γ · z — p = 0 . Отсюда получаем, что расстояние M 1 H 1 с точкой M 1 ( x 1 , y 1 , z 1 ) , проведенной на плоскость χ , вычисляемое по формуле M 1 H 1 = cos α · x + cos β · y + cos γ · z — p . Эта формула справедлива, так как это установлено благодаря теореме.
Если задана точка M 1 ( x 1 , y 1 , z 1 ) в трехмерном пространстве, имеющая нормальное уравнение плоскости χ вида cos α · x + cos β · y + cos γ · z — p = 0 , тогда вычисление расстояния от точки до плоскости M 1 H 1 производится из формулы M 1 H 1 = cos α · x + cos β · y + cos γ · z — p , так как x = x 1 , y = y 1 , z = z 1 .
Доказательство теоремы сводится к нахождению расстояния от точки до прямой. Отсюда получаем, что расстояние от M 1 до плоскости χ — это и есть модуль разности числовой проекции радиус-вектора M 1 с расстоянием от начала координат к плоскости χ . Тогда получаем выражение M 1 H 1 = n p n → O M → — p . Нормальный вектор плоскости χ имеет вид n → = cos α , cos β , cos γ , а его длина равняется единице, n p n → O M → — числовая проекция вектора O M → = ( x 1 , y 1 , z 1 ) по направлению, определяемым вектором n → .
Применим формулу вычисления скалярных векторов. Тогда получаем выражение для нахождения вектора вида n → , O M → = n → · n p n → O M → = 1 · n p n → O M → = n p n → O M → , так как n → = cos α , cos β , cos γ · z и O M → = ( x 1 , y 1 , z 1 ) . Координатная форма записи примет вид n → , O M → = cos α · x 1 + cos β · y 1 + cos γ · z 1 , тогда M 1 H 1 = n p n → O M → — p = cos α · x 1 + cos β · y 1 + cos γ · z 1 — p . Теорема доказана.
Отсюда получаем, что расстояние от точки M 1 ( x 1 , y 1 , z 1 ) к плоскости χ вычисляется при помощи подстановки в левую часть нормального уравнения плоскости cos α · x + cos β · y + cos γ · z — p = 0 вместо х , у , z координаты x 1 , y 1 и z 1 ,относящиеся к точке М 1 , взяв абсолютную величину полученного значения.
Рассмотрим примеры нахождения расстояния от точки с координатами до заданной плоскости.
Вычислить расстояние от точки с координатами M 1 ( 5 , — 3 , 10 ) к плоскости 2 x — y + 5 z — 3 = 0 .
Решим задачу двумя способами.
Первый способ начнется с вычисления направляющего вектора прямой a . По условию имеем, что заданное уравнение 2 x — y + 5 z — 3 = 0 является уравнением плоскости общего вида, а n → = ( 2 , — 1 , 5 ) является нормальным вектором заданной плоскости. Его применяют в качестве направляющего вектора прямой a , которая перпендикулярна относительно заданной плоскости. Следует записать каноническое уравнение прямой в пространстве, проходящее через M 1 ( 5 , — 3 , 10 ) с направляющим вектором с координатами 2 , — 1 , 5 .
Уравнение получит вид x — 5 2 = y — ( — 3 ) — 1 = z — 10 5 ⇔ x — 5 2 = y + 3 — 1 = z — 10 5 .
Следует определить точки пересечения. Для этого нежно объединить уравнения в систему для перехода от канонического к уравнениям двух пересекающихся прямых. Данную точку примем за Н 1 . Получим, что
x — 5 2 = y + 3 — 1 = z — 10 5 ⇔ — 1 · ( x — 5 ) = 2 · ( y + 3 ) 5 · ( x — 5 ) = 2 · ( z — 10 ) 5 · ( y + 3 ) = — 1 · ( z — 10 ) ⇔ ⇔ x + 2 y + 1 = 0 5 x — 2 z — 5 = 0 5 y + z + 5 = 0 ⇔ x + 2 y + 1 = 0 5 x — 2 z — 5 = 0
После чего необходимо разрешить систему
x + 2 y + 1 = 0 5 x — 2 z — 5 = 0 2 x — y + 5 z — 3 = 0 ⇔ x + 2 y = 1 5 x — 2 z = 5 2 x — y + 5 z = 3
Обратимся к правилу решения системы по Гауссу:
1 2 0 — 1 5 0 — 2 5 2 — 1 5 3
1 2 0 — 1 0 — 10 — 2 10 0 — 5 5 5
1 2 0 — 1 0 — 10 — 2 10 0 0 6 0 ⇒ ⇒ z = 0 6 = 0 , y = — 1 10 · 10 + 2 · z = — 1 , x = — 1 — 2 · y = 1
Получаем, что H 1 ( 1 , — 1 , 0 ) .
Производим вычисления расстояния от заданной точки до плоскости. Берем точки M 1 ( 5 , — 3 , 10 ) и H 1 ( 1 , — 1 , 0 ) и получаем
M 1 H 1 = ( 1 — 5 ) 2 + ( — 1 — ( — 3 ) ) 2 + ( 0 — 10 ) 2 = 2 30
Второй способ решения заключается в том, чтобы для начала привести заданное уравнение 2 x — y + 5 z — 3 = 0 к нормальному виду. Определяем нормирующий множитель и получаем 1 2 2 + ( — 1 ) 2 + 5 2 = 1 30 . Отсюда выводим уравнение плоскости 2 30 · x — 1 30 · y + 5 30 · z — 3 30 = 0 . Вычисление левой части уравнения производится посредствам подстановки x = 5 , y = — 3 , z = 10 , причем нужно взять расстояние от M 1 ( 5 , — 3 , 10 ) до 2 x — y + 5 z — 3 = 0 по модулю. Получаем выражение:
M 1 H 1 = 2 30 · 5 — 1 30 · — 3 + 5 30 · 10 — 3 30 = 60 30 = 2 30
Когда плоскость χ задается одним из способов раздела способы задания плоскости, тогда нужно для начала получить уравнение плоскости χ и вычислять искомое расстояние при помощи любого метода.
В трехмерном пространстве задаются точки с координатами M 1 ( 5 , — 3 , 10 ) , A ( 0 , 2 , 1 ) , B ( 2 , 6 , 1 ) , C ( 4 , 0 , — 1 ) . Вычислить расстяние от М 1 к плоскости А В С .
Для начала необходимо записать уравнение плоскости, проходящее через заданные три точки с координатами M 1 ( 5 , — 3 , 10 ) , A ( 0 , 2 , 1 ) , B ( 2 , 6 , 1 ) , C ( 4 , 0 , — 1 ) .
x — 0 y — 2 z — 1 2 — 0 6 — 2 1 — 1 4 — 0 0 — 2 — 1 — 1 = 0 ⇔ x y — 2 z — 1 2 4 0 4 — 2 — 2 = 0 ⇔ ⇔ — 8 x + 4 y — 20 z + 12 = 0 ⇔ 2 x — y + 5 z — 3 = 0
Отсюда следует, что задача имеет аналогичное предыдущему решение. Значит, расстояние от точки М 1 к плоскости А В С имеет значение 2 30 .
Нахождение расстояния от заданной точки на плоскости или к плоскости, которым они параллельны, удобнее, применив формулу M 1 H 1 = cos α · x 1 + cos β · y 1 + cos γ · z 1 — p . Отсюда получим, что нормальные уравнения плоскостей получают в несколько действий.
Найти расстояние от заданной точки с координатами M 1 ( — 3 , 2 , — 7 ) к координатной плоскости О х у z и плоскости, заданной уравнением 2 y — 5 = 0 .
Координатная плоскость О у z соответствует уравнению вида х = 0 . Для плоскости О у z оно является нормальным. Поэтому необходимо подставить в левую часть выражения значения х = — 3 и взять модуль значения расстояния от точки с координатами M 1 ( — 3 , 2 , — 7 ) к плоскости. Получаем значение, равное — 3 = 3 .
После преобразования нормальное уравнение плоскости 2 y — 5 = 0 получит вид y — 5 2 = 0 . Тогда можно найти искомое расстояние от точки с координатами M 1 ( — 3 , 2 , — 7 ) к плоскости 2 y — 5 = 0 . Подставив и вычислив, получаем 2 — 5 2 = 5 2 — 2 .
Ответ: Искомое расстояние от M 1 ( — 3 , 2 , — 7 ) до О у z имеет значение 3 , а до 2 y — 5 = 0 имеет значение 5 2 — 2 .
Источник
Расстояние от точки до плоскости (ЕГЭ 2022)
Стереометрия выглядит жутко… Вернее, сама-то стереометрия красивая!
Знаю, что, когда на уроках скучно, все мы любим порисовать на полях кубы и объемные рисунки 🙂
А вот задачи по стереометрии жутковатые. Однако, если в них хорошо разобраться, все будет легко!
Давай начнем с базы – с расстояния от точки до плоскости.
Расстояние от точки до плоскости — коротко о главном
Расстояние от точки до плоскости – длина перпендикуляра, опущенного из точки на эту плоскость.
Существует два способа найти расстояние от точки до плоскости:
Плюсы и минусы обоих способов:
| + | — | |
| АЛГ | Не нужно думать, можно просто применить несколько формул и стандартную процедуру. | Формулы громоздкие, их сложно запомнить, легко допустить ошибку. Особенно если система координат введена неудачно. |
| ГЕО | Не нужно запоминать длинных формул, вычисления обычно не длинные, арифметической ошибке трудно вкрасться. | Нужно уметь применять стереометрические теоремы и понимать, что такое доказательство. |
При алгебраическом способе для того, чтобы найти расстояние от точки до плоскости, нужно:
- Ввести систему координат;
- Найти координаты точки и уравнение плоскости;
- Применить формулу расстояния от точки до плоскости (Формулу Герона).
( displaystyle rho =frac<|<_<<_<0>>>>+<_<<_<0>>>>+<_<<_<0>>>>+D|><sqrt<<^<2>>+<^<2>>+<^<2>>>>)
( displaystyle rho )— искомое расстояние
( displaystyle left( <_<0>>;<_<0>>;<_<0>> right)) — координаты точки ( displaystyle C)
При геометрическом способе нужно:
- Построить перпендикуляр от точки до плоскости;
- Найти точку пересечения перпендикуляра с плоскостью;
- Выполнить необходимое дополнительное построение;
- Определяется расстояние от точки до точки, используя необходимые геометрические теоремы (по ситуации).
А теперь подробнее…
Расстояние от точки до плоскости
Расстояние от точки до плоскости – длина перпендикуляра, опущенного из точки на эту плоскость.
Способы нахождения расстояния от точки до плоскости
Существует, по крайней мере, два способа найти расстояние от точки до плоскости: геометрический и алгебраический.
При геометрическом способе нужно сначала понять, как расположен перпендикуляр из точки на плоскость: может он лежит в какой –то удобной плоскости, является высотой в какой-нибудь удобном (или не очень) треугольнике, а может этот перпендикуляр вообще является высотой в какой-нибудь пирамиде.
После этого первого и самого сложного этапа задача распадается на несколько конкретных планиметрических задач (быть может, в разных плоскостях).
При алгебраическом способе для того, чтобы найти расстояние от точки до плоскости, нужно ввести систему координат, найти координаты точки и уравнение плоскости, и после этого применить формулу расстояния от точки до плоскости.
Кажется с первого взгляда, что алгебраический способ легче, но это… далеко не всегда так. Проблемы обычно возникают как раз с нахождением координат точки и управления плоскости, особенно если система координат была введена не самым удобным способом. Для удобства приведём плюсы и минусы обоих способов в табличке:
| + | — | |
| АЛГ | Не нужно думать, можно просто применить несколько формул и стандартную процедуру. | Формулы громоздкие, их сложно запомнить, легко допустить ошибку. Особенно если система координат введена неудачно. |
| ГЕО | Не нужно запоминать длинных формул, вычисления обычно не длинные, арифметической ошибке трудно вкрасться. | Нужно уметь применять стереометрические теоремы и понимать, что такое доказательство |
Сейчас мы разберём один достаточно хитрый пример, двумя способами.
Задача: в кубе ( text
Геометрический способ
Куда же опускается перпендикуляр из точки ( displaystyle C) на плоскость ( displaystyle A<_<1>>M)?
Смотрим на ( displaystyle Delta A<_<1>>M) – оказывается, он равнобедренный – ( displaystyle <_<1>>M=AM)!
Проведём ( displaystyle CA) и ( displaystyle C<_<1>>). Зачем? А они тоже равны ( displaystyle CA) и ( displaystyle C<_<1>>).
Отметим точку ( displaystyle K) — середину ( displaystyle A<_<1>>) — и проведём ( displaystyle MK) и ( displaystyle CK). Треугольники ( displaystyle A<_<1>>M) и ( displaystyle A<_<1>>C) — равнобедренные, поэтому ( displaystyle MKbot A<_<1>>) и ( displaystyle CKbot A<_<1>>).
И вот теперь! Стереометрическая теорема идёт в ход: признак перпендикулярности прямой и плоскости.
Остался один шаг: проведём ( displaystyle CHbot MK) (в плоскости ( displaystyle CMK), естественно).
Что же можно сказать о ( displaystyle CH)?
( displaystyle CHbot MK) по построению
( displaystyle CHbot A<_<1>>) – так как ( displaystyle A<_<1>>bot CMK) и значит, ( displaystyle A<_<1>>) перпендикулярна всякой прямой в плоскости ( displaystyle CMK), в частности и ( displaystyle CH).
( displaystyle left< beginCHbot MK\CHbot A<_<1>>end right.Rightarrow CHbot A<_<1>>M) – Ура!
Искомый перпендикуляр из точки ( displaystyle C) на плоскость ( displaystyle A<_<1>>M) — это высота в ( displaystyle Delta CMK). Осталось найти эту высоту.
Ищем ( displaystyle KM):
Ищем ( displaystyle CK):
Теперь площадь ( displaystyle Delta KCM) по формуле Герона:
Источник
