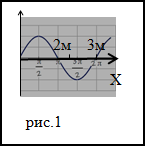
График волны функции (например, физической величины) y, распространяющейся вдоль оси Оx, построенный в фиксированный момент времени (t = const). Длина волны λ может быть измерена как расстояние между парой соседних максимумов y (x) либо минимумов, либо как удвоенное расстояние между соседними точками, в которых y = 0
Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе[1][2].
Длина́ волны́ (в линии передачи) — расстояние в линии передачи, на котором фаза электромагнитной волны вдоль направления распространения меняется на 2π[3].
Длину волны можно также определить:
- как расстояние, измеренное в направлении распространения волны, между двумя точками в пространстве, в которых фаза колебательного процесса отличается на
;
- как путь, который проходит фронт волны за интервал времени, равный периоду колебательного процесса;
- как пространственный период волнового процесса.
Представим себе волны, возникающие в воде от равномерно колеблющегося поплавка, и мысленно остановим время. Тогда длина волны — это расстояние между двумя соседними гребнями волны, измеренное в радиальном направлении. Длина волны — одна из основных характеристик волны наряду с частотой, амплитудой, начальной фазой, направлением распространения и поляризацией. Для обозначения длины волны принято использовать греческую букву 
Как правило, длина волны используется применительно к гармоническому или квазигармоническому (например, затухающему или узкополосному модулированному) волновому процессу в однородной, квазиоднородной или локально однородной среде. Однако формально длину волны можно определить по аналогии и для волнового процесса с негармонической, но периодической пространственно-временной зависимостью, содержащей в спектре набор гармоник. Тогда длина волны будет совпадать с длиной волны основной (наиболее низкочастотной, фундаментальной) гармоники спектра.
Длина волны — пространственный период волнового процесса[править | править код]
Волна — колебательный процесс, развивающийся (распространяющийся) в пространстве и во времени, в связи с этим изменяющаяся в волновом процессе физическая величина является функцией пространственных координат и времени (то есть особого вида пространственно-временной функцией). Волновой процесс в частности может быть периодическим (например, гармоническим). По аналогии с периодом колебаний 





Связь с частотой[править | править код]
Получить соотношение, связывающее длину волны с фазовой скоростью 


Для электромагнитных волн в вакууме скорость 



Радиоволны делят на диапазоны по значениям длин волн, например, 10…100 м — декаметровые (короткие) волны, 1…10 м — метровые, 0.1…1,0 м — дециметровые и т. п. Механизмы и условия распространения радиоволн, степень проявления эффекта дифракции, отражающие свойства объектов, предельная дальность радиосвязи и радиолокации сильно зависят от длины волны. Как правило, габаритные размеры антенн сравнимы либо (справедливо всегда для антенн направленного действия) превышают рабочую длину волны радиоэлектронного средства. Магнитная антенна средневолнового радиоприёмника имеет габарит на порядки меньше длины волны, и при этом, тем не менее, обладает пространственной селективностью.
Длина волны в среде[править | править код]
В оптически более плотной среде (слой выделен тёмным цветом) длина электромагнитной волны сокращается. Синяя линия — распределение мгновенного (t = const) значения напряжённости поля волны вдоль направления распространения. Изменение амплитуды напряжённости поля, обусловленное отражением от границ раздела и интерференцией падающей и отражённых волн, на рисунке условно не показано.
Длина электромагнитной волны в среде короче, чем в вакууме:
- где
— показатель преломления среды;
— относительная диэлектрическая проницаемость среды;
— относительная магнитная проницаемость среды.
Величины 









Напротив, длина электромагнитной волны (поперечномагнитной, поперечноэлектрической) в волноводах может быть не только больше, чем в среде с тем же значением 

Волны де Бройля[править | править код]
Волнам де Бройля также соответствует определённая длина волны. Частице с энергией 

- частота:
- длина волны:
- где
— постоянная Планка.
Примеры[править | править код]
Приближённо, с погрешностью около 0,07 % рассчитать длину радиоволны в свободном пространстве можно так: 300 000 делим на частоту в килогерцах, получаем длину волны в метрах. Другой способ — запомнить какую-нибудь удобную пару 

Примеры характерных частот и длин волн: частоте 50 Гц (частота тока в электросети) соответствует длина радиоволны 6000 км; частоте 100 МГц (радиовещательный FM-диапазон) — 3 м; 900 (1800) МГц (мобильные телефоны) —
33,3 (16,7) см; 2,4 ГГц (Wi-Fi) — 12,5 см; 10 ГГц (бортовые радиолокационные станции системы управления вооружением современных самолётов-истребителей) — 3 см. Видимый свет представляет собой электромагнитное излучение c длинами волн от 380 до 780 нм[4].
Примечания[править | править код]
- ↑ Колебания и волны // Физика : Учебник для 11 класса общеобразовательных учреждений / Г. Я. Мякишев, Б. Б. Буховцев. — 12-е изд. — М. : Просвещение, 2004. — С. 121. — 336 с. — 50 000 экз. — ISBN 5-09-013165-1.
- ↑ Определение не вполне корректно, поскольку (1) в одинаковой фазе колебания происходят и на фронте волны, и расстояние между точками на фронте может быть произвольным, в том числе и нулевым; (2) чтобы расстояние между двумя точками равнялось длине волны, колебание должно происходить не в одинаковой фазе, а со сдвигом фаз в
, и расположены точки должны быть вдоль линии распространения
- ↑ ГОСТ 18238-72. Линии передачи сверхвысоких частот. Термины и определения.
- ↑ ГОСТ 7601-78. Физическая оптика. Термины, буквенные обозначения и определения основных величин Архивная копия от 23 марта 2013 на Wayback Machine
Литература[править | править код]
- Волны де Бройля / В. И. Григорьев // Вешин — Газли. — М. : Советская энциклопедия, 1971. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 5).
- Длина волны // Дебитор — Евкалипт. — М. : Советская энциклопедия, 1972. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 8).

Длина волны — это расстояние между двумя последовательными пиками (гребнями) или впадинами. Самое высокое положение волны называется пиком. Самое нижнее положение волны называется впадиной.
Цикл — это полное колебание, например, кривая между двумя гребнями или двумя впадинами. Максимальное расстояние волны от равновесного положения называется амплитудой.
На рисунке показаны основные параметры волны, используемые в физике:

Определение и формула длины волн
Волна — это возмущение, распространяющееся от точки, в которой она возникла, в окружающую среду. Такое возмущение переносит энергию без чистого переноса вещества.

Длина представляет собой фактическое расстояние, пройденное волной, которое не всегда совпадает с расстоянием среды, или частиц, в которых распространяется волна. Ее также определяют как пространственный период волнового процесса.
Греческая буква «λ» (лямбда) в физике используется для обозначения длины в уравнениях. Она обратно пропорциональна частоте волны.

Период Т — время завершения полного колебания, единица измерения секунды (с).
Длинная волна соответствует низкой частоте, а короткая — высокой. Длина измеряется в метрах. Количество волн, излучаемых в каждую секунду, называется частотой и обратно пропорционально периоду.

У различных длин разная скорость распространения. Например, скорость света в воде равна 3/4 от скорости в вакууме.
Пространственный период волны — это расстояние, которое точка с постоянной фазой «пролетает» за интервал времени, соответствующий периоду колебаний.

Частота f — количество полных колебаний в единицу времени. Измеряется в Герцах (Гц).
При одном полном колебании в секунду f = 1 Гц; при 1000 колебаний в секунду f = 1 килогерц (кГц); 1 млн. колебаний в секунду f = 1 мегагерц (1 МГц).
- Зная, что скорость света в вакууме с — 300 000 км/с, или 300 000 000 м/с, то для перевода длины волны в частоту нужно 3 х 108 м/с поделить на длину в метрах.
- Единицы измерения длины волны λ — нанометры и ангстремы, где нанометр является миллиардной частью метра (1 м = 109 нм) и ангстрем является десятимиллиардной частью метра (1 м = 1010 А), то есть нанометр эквивалентен 10 ангстрем (1 нм = 10 А).

Свет, который исходит от Солнца, является электромагнитным излучением, которое движется со скоростью 300 000 км/с, но длина не одинакова для любого фотона, а колеблется между 400 нм и 700 нм. Длина световой волны влияет на цвет.
Белый свет разлагается на спектр различных цветных полос, каждая из которых определяется своей длиной волны. Таким образом, светом с наименьшей длиной является фиолетовый, который составляет около 400 нм, а светом с наибольшей длиной — красный, который составляет около 700 нм.
Таблица показывает длину волны в зависимости от цвета:

Излучения с длиной меньше фиолетового называются ультрафиолетовым излучением, рентгеновским и гамма-лучами в порядке уменьшения. Излучения больше красного называются инфракрасными, микроволнами и радиоволнами, в порядке возрастания.
Предельная дальность связи зависит от длины. Размеры антенны часто превышают рабочую длину радиоэлектронного средства.
Рисунок показывает длину волн и частоту (нм), исходящих от различных источников:

Примеры расчета длины волны для звуковых, электромагнитных и радиоволн
Задача №1
Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?
Задача №2
Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с. прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны.
Задача №3
Голосовые связки певца, поющего тенором (высоким мужским голосом), колеблются с частотой от 130 до 520 Гц. Определите максимальную и минимальную длину излучаемой звуковой волны в воздухе. Скорость звука в воздухе 330 м/с.
Источник: https://nauka.club/fizika/dlina-volny.html
Теория радиоволн: ликбез

Радиоволна

«УКВ», «ДВ», «СВ»
Сверхдлинные волны — v = 3—30 кГц (λ = 10—100 км).
Имеют свойство проникать вглубь толщи воды до 20 м и в связи с этим применяются для связи с подводными лодками, причем, лодке не обязательно всплывать на эту глубину, достаточно выкинуть радио буй до этого уровня.
Эти волны могут распространяться вплоть до огибания земли, расстояние между земной поверхностью и ионосферой, представляет для них «волновод», по которому они беспрепятственно распространяются.
Длинные волны(ДВ) v = 150—450 кГц (λ = 2000—670 м).

Средние волны (СВ) v = 500—1600 кГц (λ = 600—190 м).

Короткие волны (КВ) v= 3—30 МГц (λ = 100—10 м).

Ультракороткие Волны(УКВ) v = 30 МГц — 300 МГц (λ = 10—1 м).

Так к примеру при радиотрансляции с останкинской телебашни высотой 500 м на приемную антенну высотой 10 м, дальность связи при условии прямой видимости составит около 100 км.
Высокие частоты (ВЧ-сантиметровый диапазон) v = 300 МГц — 3 ГГц (λ = 1—0,1 м).
Не огибают препятствия и имеют хорошую проникающую способность. Используются в сетях сотовой связи и wi-fi сетях. Еще одной интересной особенностью волн этого диапазона, является то, что молекулы воды, способны максимально поглощать их энергию и преобразовывать ее в тепловую. Этот эффект используется в микроволновых печах. Как видите, wi-fi оборудование и микроволновые печи работают в одном диапазоне и могут воздействовать на воду, поэтому, спать в обнимку с wi-fi роутером, длительное время не стоит.
Крайне высокие частоты (КВЧ-миллиметровый диапазон) v = 3 ГГц — 30 ГГц (λ = 0,1—0,01 м).
Отражаются практически всеми препятствиями, свободно проникают через ионосферу. За счет своих свойств используются в космической связи.
AM — FM
Зачастую, приемные устройства имеют положения переключателей am-fm, что же это такое:
AM — амплитудная модуляция

FM — частотная модуляция

Еще термины
Интерференция — в результате отражений волн от различных препятствий, волны складываются. В случае сложения в одинаковых фазах, амплитуда начальной волны может увеличиться, при сложении в противоположных фазах, амплитуда может уменьшиться вплоть до нуля.
Это явление более всего проявляется при приеме УКВ ЧМ и ТВ сигнала. Поэтому, к примеру внутри помещения качество приема на комнатную антенну ТВ сильно «плавает».
Дифракция — явление, возникающее при встрече радиоволны с препятствиями, в результате чего, волна может менять амплитуду, фазу и направление.
Данное явление объясняет связь на КВ и СВ через ионосферу, когда волна отражается от различных неоднородностей и заряженных частиц и тем самым, меняет направление распространения. Этим же явлением объясняется способность радиоволн распространяться без прямой видимости, огибая земную поверхность. Для этого длина волны должна быть соразмерна препятствию.
PS:
Источник: https://habr.com/post/158161/
Познавательно-развлекательный сайт с техническим уклоном для работы, развлечения и отдыха

Количество нолей : введите число и скопируйте / вставьте нули, например … 220 (Гц) и 000 = 220 КГц … 42 (Гц) и 000000 = 42 МГц …
2.4 (Гц) и 000000000 = 2.4 ГГц / или 2400 МГц … // первый знак разряда после запятой заменяет первый ноль (без точки!) … (можно ввести 24 и удалить последний ноль, кому как удобно) …
000 = КГц
000000 = МГц
000000000 = ГГц
то есть, 1 ГГц = 1000 МГц = 1000000 КГц = 1000000000 Гц …
Сброс / Обновить :: Калькулятор вычисления по формуле длины волны в частоту
Сброс / Обновить …
Примечание к расчетам табличных формул
- Значение скорости света / волны примерное = 300000 км/сек
- точное = 299792458 м/с.
Калькулятор перевода частоты в длину радиоволны. Калькулятор может применяться для расчета антенн, телевизионных, радиолюбительских и радиотехнических расчетов.
Для удобства просмотра на экранах мобильных телефонов и планшетов таблица сделана вертикально.
В таблицу добавлены нестандартные значения λ для облегчения расчетов.
Наиболее востребованные и популярные частоты
Наиболее востребованные и популярные частоты, используемые в радио / технической практике и расчетах длины wave :
В диапазоне КГц : 1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 16, 20, 22, 24, 30, 32, 40, 48, 50, 64, 100, 125 …
В диапазоне МГц : 1, 2, 3, 4, 5, 6, 7, 8, 10, 16, 20, 27, 50, 60, 100, 144, 145, 400, 433, 800, 900, 1333, 1600, 1800, 2400 …
В диапазоне ГГц : 1 ; 1.1 ; 1.3 ; 1.4 ; 1.6 ; 1.8 ; 2 ; 2.1 ; 2.2 ; 2.3 ; 2.4 ; 2.5 ; 2.8 ; 3 ; 3.4 ; 4 ; 4.5 ; 5 ; 6 ; 7 ; 8 ; 10 ; 15 …
Калькулятор был разработан (без небольших исправлений) 11.10.2017 …
Что такое radiowave и ее характеристики?
Природа, в понятии суть Вселенной — не любит прямых углов … Нет, конечно — природа не избегает, однозначно, прямых углов и острых граней в строительстве мира … Но, ее живая, в постоянном движении, структура — истирает грани до округлости … Ээлектромагнитные колебания, базирующиеся на волновой структуре природы — полностью повторяют все ее многообразие …
Electromagnetic oscillation — одно из самых известных и не изученных до конца (не классифицированных) явлений мироздания … Двигаясь, из точки рождения — возмущение среды с переносом энергии совершает равноудаленные колебательные движения, синхронизированные скоростью ее распространения …
Волновые зависимости скорости, частоты и длины отражены описанием математической формулы …
Исходя из многообразия, длина волны λ также имеет множественные определения : — как, кратчайшее расстояние между двумя точками колебания в одинаковой фазе … — как, изменение фазы колебаний волны на 2π (где, 2π — не что иное, как — круг) … — как, путь фронта волны, равный периоду колебательного процесса …
Длина радиоволн является первой сравнительной характеристикой, от которых зависит длина вибраторов / габаритов антенны ; и конструкция напрямую предопределяет, какая будет частота электромагнитного колебания приема / передачи … Однако — необязательно длина вибратора антенны должна быть равной длине radiowave : прекрасно работают антенны, где частота electromagnetic oscillation выбрана от &lambda / 2, &lambda / 4 и даже с дробными значениями …
Кроме прямых углов — природа не терпит пустоты …
Эта особенность объясняет, почему колебания возмущения среды с переносом энергии не расширяются до бесконечности : сама природа, породившая perturbation with energy transfer — стремится противодействовать ее движениям, стремясь к равновесию и балансу сил, тем активнее, чем выше частота, амплитуда и скорость волнообразных колебаний … Перефразируя размышления Н. Теслы, можно сказать : кто познает природу волны — тот познает природу материи и мироздания …
18:43 31.08.2019
Контакт моя страница, общение по работе и дружба
Познавательные развлечения. Техника. Технологии. Сайт techstop-ekb.ru




techstop-ekb.ru — обзор.
Index Of — список всего.
* Меню раздела *
© techstop-ekb.ru, www, 2020.
Источник: https://techstop-ekb.ru/radio/calc-freqwave.htm
Звуковые волны, виды, длина волны и скорость звука
Сегодня мы продолжим изучать звук и разберёмся что такое звуковые волны, какие бывают их виды, что такое длина волны и какая скорость у звука.
Звуковые волны
Звук создаётся с помощью механических колебаний голосового аппарата или различных элементов музыкальных инструментов. Подробнее о механических колебаниях мы говорили вот в этой статье (читать).
Распространяется звук посредством передачи энергии механических колебаний частицам среды в виде звуковых волн. Как это происходит написано вот здесь.
Виды звуковых волн
Звуковые волны делятся на продольные. Это когда направление движения частиц совпадает с направлением распространения энергии механических колебаний в упругой среде. И на поперечные. Это когда направление движения частиц перпендикулярно распространению возмущения.
В газах (к ним относится и воздух) распространяются только продольные волны, в твердых могут быть оба вида.
Скорость звуковой волны
Если сделать движение рукой туда и обратно, то с воздухом ничего особенного не произойдет, кроме того, что его частицы сместятся в пространстве. Если бы мы могли махать рукой сто раз в секунду, то произошло бы совсем другое. У воздуха не было бы времени освобождать путь движущейся руки. И он стал бы сжиматься, когда рука движется вперёд и разрежаться, когда она возвращалась.
Благодаря упругости в процессе таких колебаний при движении поверхности тела вперёд каждая частица воздуха толкает находящуюся впереди частицу, та следующую и т. д. При обратном движении поверхности тела сжатие сменяется разряжением, за которым опять следует сжатие.
Эти волны сжатия и разряжения передаются от одного участка к другому с определённой скоростью.
В упругой среде они распространяются со скоростью, зависящей от материала среды и от того, насколько близко расположены друг к другу его атомы и молекулы.
В газах плотность не влияет на скорость. Например, в воздухе важным параметром является его температура. Но об этом ещё поговорим.
Отметим, что скорость звука в воздухе абсолютно не зависит от числа колебаний поверхности тела. Напомним, что число колебаний в секунду (точнее один период) называется Герц (Гц).
Также скорость смещения частиц и скорость звуковой волны это совершенно разные величины. Скорость частиц зависит от частоты и амплитуды звукового сигнала.
А скорость звука только от свойств среды (температура, плотность, упругость).
Формулы
Зависимость скорости звуковой волны от свойств среды, где она распространяется, рассматривается по формуле:
E — коэффициент упругости среды, определяет силу взаимодействия частиц друг с другом; p = m/V (кг/м³) — плотность среды. У твердых тел упругость больше, чем у жидкости и газа. Поэтому соотношение скоростей звука будет таким:
Скорость звука в газах может быть представлена следующей формулой:
- γ = cp/сv — отношение удельной теплоёмкости при постоянном давлении к удельной теплоёмкости при постоянном объёме.
- P атм — атмосферное давление, которое связано с температурой газообразной среды.
- Главное, что нужно понять из этой формулы, это то, что в газообразной среде скорость звука сильно зависит от температуры (чем горячее, тем быстрее двигаются молекулы, имеет большую энергию и быстрее передают механическое возбуждение)
- В воздухе скорость звука (при нормальном атмосферном давлении) приближенно можно представить так:
C = (331 + 0,6 T °) м/c
- T ° — градусы Цельсия.
- Например, при температуре 20 °C скорость звука равна 343 м/с
- C = (331 + 0,6 × 20) = 343
- При 0 °C, скорость звука равна 331 м/с, при — 20 °C = 319 м/с.
Такая зависимость особенно важна для духовых музыкальных инструментов при их настройке. Поэтому их нужно прогревать перед исполнением.
Ещё важно, что связь звуковых колебаний с размерами источника звука, которые не изменяются с температурой, не означают постоянства частоты, так как последняя зависит от скорости звука, растущей с повышением температуры. Струнные в этом случае можно подстроить.
А вот вибрирующий столб во многих духовых инструментах подстроить нельзя. Ведь колебания возникают в воздушной полости инструмента, а их частота зависит от размеров полости и скорости истечения воздушных масс из неё.
Например, у флейты высота звука увеличивается на полтона при повышении температуры на 15 °C.
Если переводить в км/ч, то 343 м/с, это 1235 км/ч. Это довольно быстро для человека или автомобиля. Но мало по сравнению со скоростью света 300 000 км/c.
Заканчивая о скорости звука, отметим, что скорость звука не зависит от частоты. Так как в воздушной среде отсутствует дисперсия — зависимость скорости распространения звука от частоты. Если бы в воздухе была бы дисперсия, мы не смогли бы слушать музыку в зале: все звуки, исполненные одновременно, приходили бы к слушателю в разное время.
Длина волны
Когда происходит одно сжатие и одно разрежение плотности среды происходит один период колебания. Поэтому расстояние между двумя сжатиями или двумя разряжениями звуковой волны и равно длине волны.
Если мы знаем частоту звука (количество волн в секунду), то мы можем вычислить расстояние между соседними соответствующими точками распространяющихся волн.
Допустим звук с известной нам скоростью 340 м/с имеет частоту 340 Гц. При этих параметрах длина волны будет равна 1 метру.
Формула для расчёта длины волны
А формула вычислений такая:
λ — длина волны, c — скорость, f — частота.
Конечно, эти расчеты являются приближенными. Так как мы уже знаем, что скорость звука в воздухе зависит от температуры, давления. Но на практике, чтобы рассчитать толщину звукопоглотителя для ослабления звука определённого диапазона частот или для оценки размера мембраны микрофона, этого вполне достаточно.
Музыкальные ноты имеет определённые частоты, значит и определённую длину волн. Например, у фортепиано верхняя октава создаёт звуки в районе 2 см, а нижняя около 10 м. Но дека фортепиано не очень эффективно генерирует эти звуки, в отличии, например, от органа. Почему?
Вернёмся к нашей руке. Допустим мы всё-таки наделены сверх способностями и можем махать рукой 100 раз в секунду = 100 Гц. Этот источник звука был бы всё равно несовершенен, так как часть воздуха огибала его сбоку.
Чтобы этого не было, источник для таких низких частот должен быть гораздо большего размера (например, дека фортепиано более эффективна, поскольку потери на её краях невелики, а органа ещё эффективнее). Если же вибратор колеблется очень быстро воздух не успевает растекаться по сторонам.
Поэтому для очень высоких частот даже малые поверхности могут быть эффективными излучателями звука.
Спасибо, что читаете New Style Sound. Подписывайтесь и делитесь с друзьями.
Источник: https://nssound.ru/o-zvuke-i-zvukovykh-signalakh/zvukovye-volny-vidy-dlina-volny-i-skorost-zvuka/
Основные формулы по физике — КОЛЕБАНИЯ И ВОЛНЫ
При изучении этого раздела следует иметь в виду, что колебания различной физической природы описываются с единых математических позиций. Здесь надо четко уяснить такие понятия, как гармоническое колебание, фаза, разность фаз, амплитуда, частота, период колебани.
Надо иметь в виду, что во всякой реальной колебательной системе есть сопротивления среды, т.е. колебания будут затухающими. Для характеристики затухания колебаний вводится коэффициент затухания и логарифмический декремент затухани.
Если колебания совершаются под действием внешней, периодически изменяющейся силы, то такие колебания называют вынужденными. Они будут незатухающими. Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы. При приближении частоты вынужденных колебаний к частоте собственных колебаний амплитуда вынужденных колебаний резко возрастает. Это явление называется резонансом.
Переходя к изучению электромагнитных волн нужно четко представлять, что электромагнитная волна — это распространяющееся в пространстве электромагнитное поле. Простейшей системой, излучающей электромагнитные волны, является электрический диполь. Если диполь совершает гармонические колебания, то он излучает монохроматическую волну.
Смотрите также основные формулы квантовой физики
Таблица формул: колебания и волны
| Физические законы, формулы, переменные | Формулы колебания и волны |
|

|
| Связь между периодом и круговой частотой: | |
| Частота: | |
| Связь круговой частоты с частотой: | |
|
|
| Частота собственных колебаний: | |
|
|
|
Уравнение затухающих колебаний: е = 2,71… — основание натуральных логарифмов. |
|
|
|
|
|
| Частота затухающих колебаний ω: | |
| Период затухающих колебаний Т: | |
| Логарифмический декремент затухания: | |
| Связь логарифмического декремента χ и коэффициента затухания β: | |
|
|
| Резонансная частота | |
| Резонансная амплитуда | |
| Полная энергия колебаний: | |
|
|
|
|
| Связь разности фаз Δφ колебаний двух точек среды с расстоянием Δх между точками среды: |
Источник: https://infotables.ru/fizika/94-osnovnye-formuly-po-fizike-kolebaniya-i-volny
Карта сайта
ЧТО ТАКОЕ РАДИОВОЛНЫ
Радиоволны – это электромагнитные колебания, распространяющиеся в пространстве со скоростью света (300 000 км/сек). Кстати, свет это тоже электромагнитные волны, обладающие схожими с радиоволнами свойствами (отражение, преломление, затухание и т.п.).
Радиоволны переносят через пространство энергию, излучаемую генератором электромагнитных колебаний. А рождаются они при изменении электрического поля, например, когда через проводник проходит переменный электрический ток или когда через пространство проскакивают искры, т.е. ряд быстро следующих друг за другом импульсов тока.
Электромагнитное излучение характеризуется частотой, длиной волны и мощностью переносимой энергии.
Частота электромагнитных волн показывает, сколько раз в секунду изменяется в излучателе направление электрического тока и, следовательно, сколько раз в секунду изменяется в каждой точке пространства величина электрического и магнитного полей.
Измеряется частота в герцах (Гц) – единицах названных именем великого немецкого ученого Генриха Рудольфа Герца. 1 Гц – это одно колебание в секунду, 1 мегагерц (МГц) – миллион колебаний в секунду.
Зная, что скорость движения электромагнитных волн равна скорости света, можно определить расстояние между точками пространства, где электрическое (или магнитное) поле находится в одинаковой фазе. Это расстояние называется длиной волны. Длина волны в метрах рассчитывается по формуле:
или примерно ,где f – частота электромагнитного излучения в МГц.
Из формулы видно, что, например, частоте 1 МГц соответствует длина волны ок. 300 м. С увеличением частоты длина волны уменьшается, с уменьшением – догадайтесь сами. В дальнейшем мы убедимся, что длина волны напрямую влияет на длину антенны для радиосвязи.
Электромагнитные волны свободно проходят через воздух или космическое пространство (вакуум).
Но если на пути волн встречается металлический провод, антенна или любое другое проводящее тело, то они отдают ему свою энергию, вызывая тем самым в этом проводнике переменный электрический ток.
Но не вся энергия волны поглощается проводником, часть ее отражается от его поверхности и либо уходит обратно, либо рассеивается в пространстве. Кстати, на этом основано применение электромагнитных волн в радиолокации.
Еще одним полезным свойством электромагнитных волн является их способность огибать на своем пути некоторые препятствия. Но это возможно лишь в том случае, когда размеры объекта меньше, чем длина волны, или сравнимы с ней.
Например, чтобы обнаружить самолет, длина радиоволны локатора должна быть меньше его геометрических размеров (менее 10 м). Если же тело больше, чем длина волны, оно может отразить ее. Но может и не отразить.
Вспомните военную технологию снижения заметности «Stealth», в рамках которой разработаны соответствующие геометрические формы, радиопоглощающие материалы и покрытия для уменьшения заметности объектов для локаторов.
Энергия, которую несут электромагнитные волны, зависит от мощности генератора (излучателя) и расстояния до него.
По научному это звучит так: поток энергии, приходящийся на единицу площади, прямо пропорционален мощности излучения и обратно пропорционален квадрату расстояния до излучателя.
Это значит, что дальность связи зависит от мощности передатчика, но в гораздо большей степени от расстояния до него.
РАСПРЕДЕЛЕНИЕ СПЕКТРА
Радиоволны, используемые в радиотехнике, занимают область, или более научно – спектр от 10 000 м (30 кГц) до 0.1 мм (3 000 ГГц). Это только часть обширного спектра электромагнитных волн.
За радиоволнами (по убывающей длине) следуют тепловые или инфракрасные лучи.
После них идет узкий участок волн видимого света, далее – спектр ультрафиолетовых, рентгеновских и гамма лучей – все это электромагнитные колебания одной природы, отличающиеся только длиной волны и, следовательно, частотой.
Хотя весь спектр разбит на области, границы между ними намечены условно. Области следуют непрерывно одна за другой, переходят одна в другую, а в некоторых случаях перекрываются.
Международными соглашениями весь спектр радиоволн, применяемых в радиосвязи, разбит на диапазоны:
|
Диапазон частот |
Наименование диапазона частот |
Наименование диапазона волн |
Длина волны |
| 3–30 кГц | Очень низкие частоты (ОНЧ) | Мириаметровые | 100–10 км |
| 30–300 кГц | Низкие частоты (НЧ) | Километровые | 10–1 км |
| 300–3000 кГц | Средние частоты (СЧ) | Гектометровые | 1–0.1 км |
| 3–30 МГц | Высокие частоты (ВЧ) | Декаметровые | 100–10 м |
| 30–300 МГц | Очень высокие частоты (ОВЧ) | Метровые | 10–1 м |
| 300–3000 МГц | Ультравысокие частоты (УВЧ) | Дециметровые | 1–0.1 м |
| 3–30 ГГц | Сверхвысокие частоты (СВЧ) | Сантиметровые | 10–1 см |
| 30–300 ГГц | Крайневысокие частоты (КВЧ) | Миллиметровые | 10–1 мм |
| 300–3000 ГГц | Гипервысокие частоты (ГВЧ) | Децимиллиметровые | 1–0.1 мм |
Но эти диапазоны весьма обширны и, в свою очередь, разбиты на участки, куда входят так называемые радиовещательные и телевизионные диапазоны, диапазоны для наземной и авиационной, космической и морской связи, для передачи данных и медицины, для радиолокации и радионавигации и т.д. Каждой радиослужбе выделен свой участок диапазона или фиксированные частоты.

Эта разбивка довольно запутана, поэтому многие службы используют свою «внутреннюю» терминологию. Обычно при обозначении диапазонов выделенных для наземной подвижной связи используются следующие названия:
| Термин | Диапазон частот | Пояснения |
| КВ | 2–30 МГц | Из-за особенностей распространения в основном применяется для дальней связи. |
| «Си-Би» | 25.6–30.1 МГц | Гражданский диапазон, в котором могут пользоваться связью частные лица. В разных странах на этом участке выделено от 40 до 80 фиксированных частот (каналов). |
| «Low Band» | 33–50 МГц | Диапазон подвижной наземной связи. Непонятно почему, но в русском языке не нашлось термина, определяющего данный диапазон. |
| УКВ | 136–174 МГц | Наиболее распространенный диапазон подвижной наземной связи. |
| ДЦВ | 400–512 МГц | Диапазон подвижной наземной связи. Иногда не выделяют этот участок в отдельный диапазон, а говорят УКВ, подразумевая полосу частот от 136 до 512 МГц. |
| «800 МГц» |
806–825 и 851–870 МГц |
Традиционный «американский» диапазон; широко используется подвижной связью в США. У нас не получил особого распространения. |
Не надо путать официальные наименования диапазонов частот с названиями участков, выделенных для различных служб. Стоит отметить, что основные мировые производители оборудования для подвижной наземной связи выпускают модели, рассчитанные на работу в пределах именно этих участков.
В дальнейшем мы будем говорить о свойствах радиоволн применительно к их использованию в наземной подвижной радиосвязи.
КАК РАСПРОСТРАНЯЮТСЯ РАДИОВОЛНЫ
Радиоволны излучаются через антенну в пространство и распространяются в виде энергии электромагнитного поля. И хотя природа радиоволн одинакова, их способность к распространению сильно зависит от длины волны.
Земля для радиоволн представляет проводник электричества (хотя и не очень хороший). Проходя над поверхностью земли, радиоволны постепенно ослабевают. Это связано с тем, что электромагнитные волны возбуждают в поверхности земли электротоки, на что и тратится часть энергии. Т.е. энергия поглощается землей, причем тем больше, чем короче длина волна (выше частота).
Кроме того, энергия волны ослабевает еще и потому, что излучение распространяется во все стороны пространства и, следовательно, чем дальше от передатчика находится приемник, тем меньшее количество энергии приходится на единицу площади и тем меньше ее попадает в антенну.
Передачи длинноволновых вещательных станций можно принимать на расстоянии до нескольких тысяч километров, причем уровень сигнала уменьшается плавно, без скачков. Средневолновые станции слышны в пределах тысячи километров.
Что же касается коротких волн, то их энергия резко убывает по мере удаления от передатчика. Этим объясняется тот факт, что на заре развития радио для связи в основном применялись волны от 1 до 30 км.
Волны короче 100 метров вообще считались непригодными для дальней связи.
Однако дальнейшие исследования коротких и ультракоротких волн показали, что они быстро затухают, когда идут у поверхности Земли. При направлении излучения вверх, короткие волны возвращаются обратно.
Еще в 1902 английский математик Оливер Хевисайд (Oliver Heaviside) и американский инженер-электрик Артур Эдвин Кеннелли (Arthur Edwin Kennelly) практически одновременно предсказали, что над Землей существует ионизированный слой воздуха – естественное зеркало, отражающее электромагнитные волны. Этот слой был назван ионосферой.
Ионосфера Земли должна была позволить увеличить дальность распространения радиоволн на расстояния, превышающие прямую видимость. Экспериментально это предположение было доказано в 1923. Радиочастотные импульсы передавались вертикально вверх и принимались вернувшиеся сигналы. Измерения времени между посылкой и приемом импульсов позволили определить высоту и количество слоев отражения.

Отразившись от ионосферы, короткие волны возвращаются к Земле, оставив под собой сотни километров «мертвой зоны». Пропутешествовав к ионосфере и обратно, волна не «успокаивается», а отражается от поверхности Земли и вновь устремляется к ионосфере, где опять отражается и т. д. Так, многократно отражаясь, радиоволна может несколько раз обогнуть земной шар.
Установлено, что высота отражения зависит в первую очередь от длины волны. Чем короче волна, тем на большей высоте происходит ее отражение и, следовательно, больше «мертвая зона». Эта зависимость верна лишь для коротковолновой части спектра (примерно до 25–30 МГц). Для более коротких волн ионосфера прозрачна. Волны пронизывают ее насквозь и уходят в космическое пространство.
Из рисунка видно, что отражение зависит не только от частоты, но и от времени суток. Это связано с тем, что ионосфера ионизируется солнечным излучением и с наступлением темноты постепенно теряет свою отражательную способность. Степень ионизации также зависит от солнечной активности, которая меняется в течение года и из года в год по семилетнему циклу.

Радиоволны УКВ диапазона по свойствам в большей степени напоминают световые лучи. Они практически не отражаются от ионосферы, очень незначительно огибают земную поверхность и распространяются в пределах прямой видимости. Поэтому дальность действия ультракоротких волн невелика.
Но в этом есть определенное преимущество для радиосвязи. Поскольку в диапазоне УКВ волны распространяются в пределах прямой видимости, то можно располагать радиостанции на расстоянии 150–200 км друг от друга без взаимного влияния.
А это позволяет многократно использовать одну и ту же частоту соседним станциям.

Свойства радиоволн диапазонов ДЦВ и 800 МГц еще более близки к световым лучам и потому обладают еще одним интересным и важным свойством. Вспомним, как устроен фонарик. Свет от лампочки, расположенной в фокусе рефлектора, собирается в узкий пучок лучей, который можно послать в любом направлении.
Примерно то же самое можно проделать и с высокочастотными радиоволнами. Можно их собирать зеркалами-антеннами и посылать узкими пучками. Для низкочастотных волн такую антенну построить невозможно, так как слишком велики были бы ее размеры (диаметр зеркала должен быть намного больше, чем длина волны).
Возможность направленного излучения волн позволяет повысить эффективность системы связи. Связано это с тем, что узкий луч обеспечивает меньшее рассеивание энергии в побочных направлениях, что позволяет применять менее мощные передатчики для достижения заданной дальности связи. Направленное излучение создает меньше помех другим системам связи, находящимся не в створе луча.
При приеме радиоволн также могут использоваться достоинства направленного излучения. Например, многие знакомы с параболическими спутниковыми антеннами, фокусирующими излучение спутникового передатчика в точку, где установлен приемный датчик.
Применение направленных приемных антенн в радиоастрономии позволило сделать множество фундаментальных научных открытий.
Возможность фокусирования высокочастотных радиоволн обеспечила их широкое применение в радиолокации, радиорелейной связи, спутниковом вещании, беспроводной передаче данных и т.п.

Необходимо отметить, что с уменьшением длины волны возрастает затухание и поглощение энергии в атмосфере. В частности на распространение волн короче 1 см начинают влиять такие явления как туман, дождь, облака, которые могут стать серьезной помехой, ограничивающей дальность связи.
Мы выяснили, что радиоволны обладают различными свойствами распространения в зависимости от длины волны и каждый участок радиоспектра применяется там, где лучше всего используются его преимущества.
Источник: http://viol.uz/radiovolnyi-i-chastotyi.html
Длина, скорость и частота электромагнитной волны
Онлайн калькулятор перевода длины волны в частоту для широкого диапазона частот, включая радиоволны, микроволны, инфракрасное излучение, видимый свет, ультрафи- олетовое излучение, рентгеновские и гамма лучи.
Электромагнитные колебания — это взаимосвязанные колебания электрического и магнитного полей, проявляющиеся в периодическом изменении напряжённости (E) и индукции (B) поля в электроцепи или пространстве. Эти поля перпендикулярны друг другу в направлении движения волны (Рис.1) и, в зависимости от частоты, представляют собой: радиоволны, микроволны, инфракрасное излучение, видимый свет, ультрафиолетовое излучение, рентгеновские либо гамма-лучи.
Длина волны, обозначаемая буквой λ и измеряемая в метрах — это расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе. Другими словами, это расстояние, на котором фаза электромагнитной волны вдоль направления распространения меняется на 2π.
Время, за которое волна успевает преодолеть это расстояние (λ), т. е. интервал времени, за который периодический колебательный процесс повторяется, называется периодом колебаний, обозначается буквой ፐ (тау) или Т и измеряется в метрах.
Частота электромагнитных колебаний связана с периодом простейшим соотношением:
f (Гц) = 1 / T (сек).
Скорость распространения электромагнитных волн в вакууме (v) равна скорости света и составляет величину: v = С = 299792458 м/сек.
В среде эта скорость уменьшается: v = С / n, где n > 1 — это показатель преломления среды. Абсолютный показатель преломления любого газа (в том числе воздуха) при обычных условиях мало чем отличается от единицы, поэтому с достаточной точностью его можно не учитывать в условиях распространения электромагнитных волн в воздушном пространстве. Соотношение, связывающее длину волны со скоростью распространения в общем случае, выглядит следующим образом:
λ (м) = v (м/сек) *Т (сек) = v (м/сек) / f (Гц).
И окончательно для воздушной среды:
λ (м) = 299792458 *Т (сек) = 299792458 / f (Гц).
Прежде чем перейти к калькуляторам, давайте рассмотрим шкалу частот и длин волн непрерывного диапазона электромагнитных волн, которая традиционно разбита на ряд поддиапазонов. Соседние диапазоны могут немного перекрываться.
| Диапазон | Полоса частот | Длина волны |
| Сверхдлинные радиоволны | 3…30 кГц | 100000…10000 м |
| Длинные радиоволны | 30…300 кГц | 10000…1000 м |
| Средние радиоволны | 300…3000 кГц | 1000…100 м |
| Короткие радиоволны | 3…30 МГц | 100…10 м |
| Метровый радиодиапазон | 30…300 МГц | 10…1 м |
| Дециметровый радиодиапазон | 300…3000 МГц | 1…0,1 м |
| Сантиметровый СВЧ диапазон | 3…30 ГГц | 10…1 см |
| Микроволновый СВЧ диапазон | 30…300 ГГц | 1…0,1 см |
| Инфракрасное излучение | 0,3…405 ТГц | 1000…0,74 мкм |
| Красный цвет | 405…480 ТГц | 740…625 нм |
| Оранжевый цвет | 480…510 ТГц | 625…590 нм |
| Жёлтый цвет | 510…530 ТГц | 590…565 нм |
| Зелёный цвет | 530…600 ТГц | 565…500 нм |
| Голубой цвет | 600…620 ТГц | 500…485 нм |
| Синий цвет | 620…680 ТГц | 485…440 нм |
| Фиолетовый цвет | 680…790 ТГц | 440…380 нм |
| Ультрафиолетовое излучение | 480…30000 ТГц | 400…10 нм |
| Рентгеновское излучение | 30000…3000000 ТГц | 10…0,1 нм |
| Гамма излучение | 3000000…30000000 ТГц | 0,1…0,01 нм |
А теперь можно переходить к калькуляторам.
КАЛЬКУЛЯТОР РАСЧЁТА ДЛИНЫ ВОЛНЫ ПО ЧАСТОТЕ
КАЛЬКУЛЯТОР РАСЧЁТА ЧАСТОТЫ ПО ДЛИНЕ ВОЛНЫ
В радиочастотной практике имеет распространение величина Kp, называемая коэффициентом укорочения. Однако здесь существует некоторая путаница.
Одни источники интерпретируют эту величину, как отношение длины волны в среде к длине волны в вакууме, т. е. численно равной Kp = 1/n, где n — это, как мы помним, показатель преломления среды.
Другие, наоборот — как отношение длины волны в вакууме к длине волны в среде, т. е. Kp = n.
Поэтому надо иметь в виду — если Kp > 1, то значение показателя преломления среды, которое следует подставлять в калькулятор n = Kp, а если Kp < 1, то n = 1/Kp.
Источник: https://vpayaem.ru/inf_wave1.html
Решу егэ
Задание 18 № 3726
Первый источник света расположен на расстоянии от точки A, а второй — на расстоянии от точки A. Источники когерентны и синфазные и испускают свет с частотой
Установите соответствие между физическими явлениями и условиями, при соблюдении которых эти явления можно наблюдать. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
| ФИЗИЧЕСКИЕ ЯВЛЕНИЯ | УСЛОВИЯ НАБЛЮДЕНИЯ |
| А) Наблюдение в точке A максимума интерференционной картиныБ) Наблюдение в точке A минимума интерференционной картины |
|
Решение.
Первым условие для наблюдения интерференции является то, что источники должны быть когерентными. Это условие здесь выполнено, а значит, будет наблюдаться устойчивая интерференционная картина.
Для того, чтобы наблюдать в некоторой точки максимум интерференционной картины, необходимо, чтобы оптическая разность хода до этой точки от двух когерентных синфазных источников равнялась целому числу длин волн, то есть должно выполняться условие:
где m — целое число (А — 1).
Для наблюдения интерференционного минимума, необходимо, чтобы оптическая разность хода до этой точки от двух когерентных синфазных источников равнялась полуцелому числу длин волн, то есть должно выполняться условие:
где m — целое число (Б — 3).
Ответ: 13.
Ответ: 13
Источник: Яндекс: Тренировочная работа ЕГЭ по физике. Вариант 1.
Источник: https://phys-ege.sdamgia.ru/test?theme=288
Содержание:
- Определение и формула длины волны
- Длина стоячей волны
- Длина бегущей волны
- Длина бегущей волны
- Длина электромагнитной волны
- Единицы измерения длины волны
- Примеры решения задач
Определение и формула длины волны
Определение
Длиной волны называют кратчайшее пространственное расстояние между ее точками, совершающими колебания в одной фазе.
Обозначают длину волны, чаще всего буквой $lambda$ .
Для синусоидальных волн $lambda$ – это расстояние, на которое волна распространяется за один период
(T). Длину волны в этом случае еще называют пространственным периодом. Тогда формулой длины волны можно считать выражение:
$$lambda=v T=frac{v}{nu}=frac{2 pi}{k}$$
где v – скорость распространения волны, $nu=frac{1}{T}$ – частота колебаний,
$k=frac{omega}{v}$ – волновое число,
$T=frac{2 pi}{omega}$ – период волны,
$omega$ – циклическая частота волны.
Длина стоячей волны
Длиной стоячей волны($lambda_{st}$) называют расстояние в пространстве между
двумя пучностями (или узлами):
$$lambda_{s t}=frac{pi}{k}=frac{lambda}{2}(2)$$
где $lambda$ – длина бегущей волны. Надо заметить, что расстояние между соседними пучностью и
узлом связывает равенство:
$$frac{lambda_{s t}}{2}=frac{lambda}{4}(3)$$
Длина бегущей волны
В бегущей волне длина волны связана с фазовой скоростью (vph) формулой:
$$lambda=frac{v_{p h}}{nu}(4)$$
Длина бегущей волны
Разность фаз и длина волны
Две точки волны находящиеся на расстоянии
$Delta x$ имеют при колебании разность
фаз ($Delta varphi$), которая равна:
$$Delta varphi=frac{2 pi Delta x}{lambda}(5)$$
Длина электромагнитной волны
Скорость распространения электромагнитных волн в вакууме равна скорости света в вакууме
($c approx 3 cdot 10^{8}$ м/с), следовательно, длина электромагнитной волны в
вакууме, может быть рассчитана при помощи формулы:
$$lambda=c T=frac{c}{nu}(6)$$
Длина электромагнитной волны в веществе равна:
$$lambda=frac{c}{n nu}(7)$$
где $n=sqrt{varepsilon mu}$ – показатель преломления вещества,
$varepsilon$ – диэлектрическая проницаемость вещества,
$mu$ – магнитная проницаемость вещества.
Отметим, что все рассматриваемые формулы относят к случаю T=const.
Единицы измерения длины волны
Основной единицей измерения длины волны в системе СИ является: [$lambda$]=м
В СГС: [$lambda$]=см
Примеры решения задач
Пример
Задание. Каково приращение длины электромагнитной волны, имеющей частоту v=1 МГц при ее переходе в немагнитную среду,
которая имеет диэлектрическую проницаемость $varepsilon$=2?
Решение. Так как речь в условии задачи идет о немагнитной среде, в которую переходит волна, то считаем магнитную
проницаемость вещества равной единице ($mu$=1).
Длина рассматриваемой нами волны в вакууме равна:
$$lambda_{1}=frac{c}{nu}(1.1)$$
Длина волны в веществе:
$$lambda_{2}=frac{c}{n nu}=frac{c}{sqrt{varepsilon mu} cdot nu}(1.2)$$
Используя выражения (1.1) и (1.2) найдем изменение длины волны:
$$Delta lambda=lambda_{2}-lambda_{1}=frac{c}{sqrt{varepsilon mu} cdot nu}-frac{c}{nu}=frac{c}{nu}left(frac{1}{sqrt{varepsilon mu}}-1right)$$
Проведем вычисления, если нам известно помимо данных приведенных в условии задачи, что
$c approx 3 cdot 10^{8}$ м/с- скорость света в вакууме, и v=1 МГц=106 Гц:
$$Delta lambda=frac{3 cdot 10^{8}}{10^{6}}left(frac{1}{sqrt{4 cdot 1}}-1right)=-1,5 cdot 10^{2}(mathrm{~m})$$
Ответ. Длина волны уменьшится на 150 м

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Какова длина плоской синусоидальной волны, которая распространяется по оси X. Две точки, которые
находятся на оси X расположенные на расстояниях 2 м и 3 м от источника совершают колебания с разностью фаз равной
$Delta varphi=frac{3 pi}{5}$ . Каким будет период колебаний в волне, если ее скорость в данной среде равна v=2м/с?
Решение. Сделаем рисунок.
Основой для решения задачи будет формула:
$$Delta varphi=frac{2 pi Delta x}{lambda}=frac{2 pileft(x_{2}-x_{1}right)}{lambda}(2.1)$$
Выразим из (2.1) искомую длину волны, получим:
$$lambda=frac{2 pileft(x_{2}-x_{1}right)}{Delta varphi}(2.2)$$
Период колебаний связан с длиной волны формулой:
$$T=frac{lambda}{v}(2.3)$$
C учетом (2.2), имеем:
$$T=frac{2 pileft(x_{2}-x_{1}right)}{Delta varphi v}$$
Проведем вычисления:
$$
begin{array}{c}
lambda=frac{2 pi(3-2)}{3 pi} cdot 5=frac{10}{3}(m) \
T=frac{10}{3 cdot 2}=1,67(c)
end{array}
$$
Ответ. $lambda approx 3,3 mathrm{~m} ; T approx 1,67 mathrm{c}$
Читать дальше: Формула количества теплоты.
Загрузить PDF
Загрузить PDF
Длина волны – это расстояние между двумя соседними точками, которые колеблются в одной фазе; как правило, понятие “длина волны” ассоциируется с электромагнитным спектром.[1]
Метод вычисления длины волны зависит от данной информации. Воспользуйтесь основной формулой, если известны скорость и частота волны. Если нужно вычислить длину световой волны по известной энергии фотона, воспользуйтесь соответствующей формулой.
-
1
Воспользуйтесь формулой для вычисления длины волны. Чтобы найти длину волны, разделите скорость волны на частоту. Формула:
[2]
-
2
Используйте соответствующие единицы измерения. Скорость измеряется в единицах метрической системы, например, в километрах в час (км/ч), метрах в секунду (м/с) и так далее (в некоторых странах скорость измеряется в британской системе, например, в милях в час). Длина волны измеряется в нанометрах, метрах, миллиметрах и так далее. Частота, как правило, измеряется в герцах (Гц).[3]
- Единицы измерения конечного результата должны соответствовать единицам измерения исходных данных.
- Если частота дана килогерцах (кГц), или скорость волны в километрах в секунду (км/с), преобразуйте данные значения в герцы (10 кГц = 10000 Гц) и в метры в секунду (м/с).
-
3
Известные значения подставьте в формулу и найдите длину волны. В приведенную формулу подставьте значения скорости и частоты волны. Разделив скорость на частоту, вы получите длину волны.[4]
- Например. Найдите длину волны, распространяющейся со скоростью 20 м/с при частоте колебаний 5 Гц.
-
4
Реклама
-
1
-
2
Перепишите представленную формулу, чтобы найти длину волны. Для этого проделайте ряд математических операций. Обе стороны формулы умножьте на длину волны, а затем обе стороны разделите на энергию; вы получите формулу:
. Если энергия фотона известна, можно вычислить длину световой волны.[7]
- Эту формулу можно использовать для вычисления максимальной длины световой волны, необходимой для ионизации металлов. В формулу подставьте энергию, необходимую для ионизации, и вычислите длину волны.[8]
- Эту формулу можно использовать для вычисления максимальной длины световой волны, необходимой для ионизации металлов. В формулу подставьте энергию, необходимую для ионизации, и вычислите длину волны.[8]
-
3
В полученную формулу подставьте известные значения и вычислите длину волны. В формулу подставьте только значение энергии, потому что две константы являются постоянными величинами, то есть не меняются. Чтобы найти длину волны, перемножьте константы, а затем результат разделите на энергию.[9]
- Например. Найдите длину световой волны, если энергия фотона равна 2,88 x 10-19 Дж.
Реклама
-
1
Проверьте ответ. Для этого умножьте длину волны на частоту. Если вы получите данное значение скорости, решение правильное; в противном случае проверьте вычисления. Если вы пользуетесь калькулятором, правильно вводите числа.
- Например. Найдите длину волны, которая распространяется со скоростью 343 м/с при частоте колебаний 70 Гц.
- Решите эту задачу как описано выше и получите значение 4,9 м.
- Проверьте ответ: 4,9 м х 70 Гц = 343 м/сек. Это данная в условии задачи скорость, поэтому решение верное.
- Например. Найдите длину волны, которая распространяется со скоростью 343 м/с при частоте колебаний 70 Гц.
-
2
Используйте экспоненциальную запись чисел, чтобы избежать ошибок при округлении чисел (в калькуляторе). Порой в вычислении длины волны участвуют очень большие числа, особенно когда присутствует скорость света. Это может привести к ошибкам округления чисел. Поэтому используйте экспоненциальную запись чисел.[10]
- Например. Свет проходит сквозь воду со скоростью 225000000 м/с. Найдите длину световой волны, если ее частота равна 4 x 1014 Гц.
-
3
Помните, что частота волны не меняется при изменении среды ее распространения. Во многих задачах волна распространяется в двух средах, и некоторые учащиеся пытаются вычислить две длины волны. Это ошибка, потому что в отличие от скорости распространения и длины волны частота волны не меняется при изменении среды ее распространения.[11]
- Например, световая волна длиной λ, распространяющаяся со скоростью v при частоте f, переходит из воздушного пространства в некоторую среду, показатель преломления которой равен 1,5. Как изменятся указанные три величины?
Реклама
Об этой статье
Эту страницу просматривали 158 119 раз.
Была ли эта статья полезной?
Каждая волна имеет свои параметры движения.
Скорость волны — скорость распространения возмущения.
Пример:
воздействуя на стальной стержень с одного конца, можно вызвать волны сжатия и разрежения со скоростью (5000 frac{м}{с}).
Скорость волны зависит от строения вещества и взаимодействия между её молекулами (атомами). Поэтому в различных средах скорость одной и той же волны будет отличаться.
Помимо скорости, важной характеристикой волны является длина волны.
Длина волны — расстояние, на которое распространяется волна за время, равное периоду колебаний в ней.
Рассмотрим процесс передачи колебаний от точки к точке при распространении поперечной волны.
Используется модель, в которой частицы среды заменяют шариками. Для удобства их можно пронумеровать (рис. (1)).
Частицы среды связаны между собой межмолекулярными силами взаимодействия, поэтому волна передаётся от одной частицы к другой.
Рис. (1). Модель упругой среды для демонстрации колебаний
Отклоним первый шарик от положения равновесия. Силы притяжения передадут движение второму, третьему шарику. Каждый элемент вещества (молекула, атом) повторит движение первой частицы с запаздыванием, которые называют сдвигом фазы. Это запаздывание зависит от расстояния, на котором находится рассматриваемый шарик по отношению к первому шарику.
Предположим, что первый шарик достиг максимального смещения от положения равновесия (рис. (2)). В этот момент четвёртый шарик только начнет движение, следовательно, он отстаёт от первого на (1/4) колебания.
Рис. (2). Изображение максимального смещения от положения равновесия первого шарика
В момент времени, когда смещение четвертого шарика будет наибольшим (рис. (3)), седьмой шарик будет отставать от него на (1/4) колебания. А если рассмотреть отставание седьмого шарика от первого, то оно составляет (1/2) колебания.
Рис. (3). Изображение максимального смещения от положения равновесия четвёртого шарика
Между седьмым и четвёртым шариком, а также седьмым и десятым (1/4) часть колебания (рис. (4)).
Рис. (4). Изображение максимального смещения от положения равновесия седьмого шарика
Первый и тринадцатый шарик совершают одно колебание, то есть двигаются в одной фазе (рис. (5)). Это значит, что между ними все шарики с первого по двенадцатый проходят полный колебательный процесс или составляют одну волну.
Рис. (5). Изображение максимального смещения от положения равновесия десятого шарика
Начиная с тринадцатого шарика, мы можем отсчитывать новую волну (рис. (6)).
Рис. (6). Изображение модели новой волны
Длину волны измеряют расстоянием, на которое перемещается волновая поверхность за один период колебания источника волн;
Длиной волны является расстояние между двумя ближайшими точками бегущей волны на одном луче, который колеблется в одинаковой фазе:
, где (λ) («лямбда») — длина волны, (upsilon) — скорость волны, (T) — период колебания.
Период колебаний можно выразить как величину, обратную частоте колебаний:
T=1ν
.
Тогда выразим длину волны как отношение скорости и частоты:
λ=υν
.
Длина волны прямо пропорциональна скорости волны и обратно пропорциональна частоте колебаний (прямо пропорциональна периоду колебаний).
Поперечные и продольные волны описываются одними и теми же законами.
Выразим скорость волны:
как отношение длины волны к периоду колебаний:
υ=λT
;
как произведение длины волны на частоту колебаний:
υ=λν
.
За длину волны (λ) примем расстояние между шариками, колеблющимися в одинаковых фазах. Например (см. рис. (6)), между четвёртым и шестнадцатым, третьим и пятнадцатым.
Колебания проходят шарики, начиная с первого и заканчивая двенадцатым, проходят все фазы колебания. Новая волна начинается с тринадцатого шарика. Каждый шарик совершает одно полное колебание за время, которое называют периодом колебаний (T). За это время колебательный процесс проходит расстояние, называемое длиной волны (λ.)
Модель распространения продольных волн представлена на рисунке (7).
Длиной волны будет расстояние между соседними центрами сжатия пружины.
Рис. (7). Распространение продольных волн в упругой пружине
Источником колебаний генерируется волна той же частоты, поэтому вынужденные колебания совпадают по частоте с осциллятором и не зависит от плотности среды, в которой движется волна.
Если в ходе движения волна переходит в среду другой плотности, то скорость движения волны изменяется, а частота колебаний остаётся прежней.
Источники:
Рис. 1. Модель упругой среды для демонстрации колебаний. © ЯКласс.
Рис. 2. Изображение максимального смещения от положения равновесия первого шарика. © ЯКласс.
Рис. 3. Изображение максимального смещения от положения равновесия четвёртого шарика. © ЯКласс.
Рис. 4. Изображение максимального смещения от положения равновесия седьмого шарика. © ЯКласс.
Рис. 5. Изображение максимального смещения от положения равновесия десятого шарика. © ЯКласс.
Рис. 6. Изображение модели новой волны. © ЯКласс.
Рис. 7. Распространение продольных волн в упругой пружине. © ЯКласс.