Формулы скорости, времени, расстояния?
Как выразить эти понятия друг одно через другие?
Анонимный вопрос
2 ноября 2018 · 236,8 K
Если вам известна скорость v и время t, то вы сможете найти расстояние S по формуле S=vt.
Обратите внимание на единицы измерения! Если вам дана скорость в километрах в час, то и время должно быть выражено в часах (или в метрах в секунду и секундах соответственно).
Выразить скорость из этой формулы можно следующим образом: v=S/t
А если вы хотите посчитать время, то воспользуйтесь формулой t=S/v
204,0 K
Комментировать ответ…Комментировать…
V = S : t
t = S : V
S = V * t
S = расстояние
V = скорость
t = время
: = деление
* = умножение
Пример :
Решил найти расстояние ( S)
Для этого скорость ( V) которая равна 4км/ч *время ( t) 4 часа
Ответ : 16 км Читать далее
21,2 K
Подскажите а как посчитать, за если я прохожу допустим растояние 9 метров за 7 минут, то за сколько я пройду 300 метров?
Комментировать ответ…Комментировать…
Учусь в гимназии №17. Увлекаюсь математикой, русским языком, родным языком, литературой и… · 20 мая 2021
(Обратите внимание, что для записи формулы пути используются строчные буквы s, v и t. Это сделано, чтобы не путать их с обозначением площади — S и объёма — V.) Читать далее
20,0 K
Комментировать ответ…Комментировать…
Чтобы найти скорость, нужно расстояние разделить на время движения: v = S: t. Время – это продолжительность каких-то действий, событий. Время движения обозначается маленькой латинской буквой t. Чтобы найти время, нужно расстояние разделить на скорость движения: t = S: v. Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
5,7 K
Комментировать ответ…Комментировать…
Короче!
Если у вас расстояние нужно найти то:
S=t*v, S=50*20(пример)
Если нужно найти время то:
t=S:V
Если нужно найти скорость то :
V=S:T.
Это все формулы. Читать далее
59,9 K
спасибо, Warrior! Было не понятно, но
ты помог мне выровнять математику!
Комментировать ответ…Комментировать…
В данной статье рассмотрим способы определить расстояние от точки до точки теоретически и на примере конкретных задач. И для начала введем некоторые определения.
Расстояние между точками – это длина отрезка, их соединяющего, в имеющемся масштабе. Задать масштаб необходимо, чтобы иметь для измерения единицу длины. Потому в основном задача нахождения расстояния между точками решается при использовании их координат на координатной прямой, в координатной плоскости или трехмерном пространстве.
Расстояние между точками на координатной прямой
Исходные данные: координатная прямая Ox и лежащая на ней произвольная точка А. Любой точке прямой присуще одно действительное число: пусть для точки А это будет некое число хA, оно же – координата точки А.
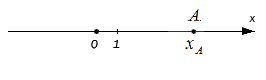
В целом можно говорить о том, что оценка длины некого отрезка происходит в сравнении с отрезком, принятым за единицу длины в заданном масштабе.
Если точке А соответствует целое действительное число, отложив последовательно от точки О до точки по прямой ОА отрезки – единицы длины, мы можем определить длину отрезка OA по итоговому количеству отложенных единичных отрезков.
К примеру, точке А соответствует число 3 – чтобы попасть в нее из точки О, необходимо будет отложить три единичных отрезка. Если точка А имеет координату -4 – единичные отрезки откладываются аналогичным образом, но в другом, отрицательном направлении. Таким образом в первом случае, расстояние ОА равно 3; во втором случае ОА = 4.
Если точка A имеет в качестве координаты рациональное число, то от начала отсчета (точка О) мы откладываем целое число единичных отрезков, а затем его необходимую часть. Но геометрически не всегда возможно произвести измерение. К примеру, затруднительным представляется отложить на координатной прямой дробь 4111.
Вышеуказанным способом отложить на прямой иррациональное число и вовсе невозможно. К примеру, когда координата точки А равна 11 . В таком случае возможно обратиться к абстракции: если заданная координата точки А больше нуля, то OA=xA (число принимается за расстояние); если координата меньше нуля, то OA=-xA . В общем, эти утверждения справедливы для любого действительного числа xA.
Резюмируя: расстояние от начала отсчета до точки, которой соответствует действительное число на координатной прямой, равно:
- 0, если точка совпадает с началом координат;
- xA , если xA>0;
- -xA , если xA<0 .
При этом очевидно, что сама длина отрезка не может быть отрицательной, поэтому, используя знак модуля, запишем расстояние от точки O до точки A с координатой xA: OA=xA
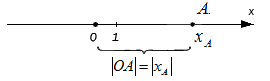
Верным будет утверждение: расстояние от одной точки до другой будет равно модулю разности координат. Т.е. для точек A и B, лежащих на одной координатной прямой при любом их расположении и имеющих соответственно координаты xA и xB : AB=xB-xA.
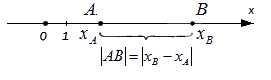
Расстояние между точками на плоскости
Исходные данные: точки A и B, лежащие на плоскости в прямоугольной системе координат Oxy с заданными координатами: A(xA, yA) и B(xB, yB) .
Проведем через точки А и B перпендикуляры к осям координат Ox и Oy и получим в результате точки проекции: Ax, Ay, Bx, By. Исходя из расположения точек А и B далее возможны следующие варианты:
– если точки А и В совпадают, то расстояние между ними равно нулю;
– если точки А и В лежат на прямой, перпендикулярной оси Ox (оси абсцисс), то точки и совпадают, а |АВ| = |АyBy|. Поскольку, расстояние между точками равно модулю разности их координат, то AyBy=yB-yA , а, следовательно AB=AyBy=yB-yA.
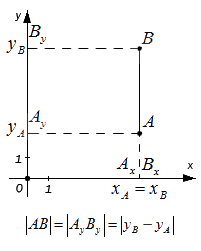
– если точки A и B лежат на прямой, перпендикулярной оси Oy (оси ординат) – по аналогии с предыдущим пунктом: AB=AxBx=xB-xA
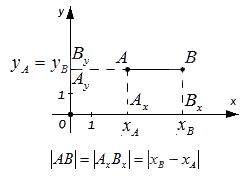
– если точки A и B не лежат на прямой, перпендикулярной одной из координатных осей, найдем расстояние между ними, выведя формулу расчета:
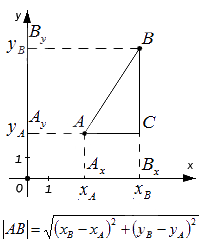
Мы видим, что треугольник АВС является прямоугольным по построению. При этом AC=AxBx и BC=AyBy. Используя теорему Пифагора, составим равенство: AB2=AC2+BC2⇔AB2=AxBx2+AyBy2 , а затем преобразуем его: AB=AxBx2+AyBy2=xB-xA2+yB-yA2=(xB-xA)2+(yB-yA)2
Сформируем вывод из полученного результата: расстояние от точки А до точки В на плоскости определяется расчётом по формуле с использованием координат этих точек
AB=(xB-xA)2+(yB-yA)2
Полученная формула также подтверждает ранее сформированные утверждения для случаев совпадения точек или ситуаций, когда точки лежат на прямых, перпендикулярных осям. Так, для случая совпадения точек A и B будет верно равенство: AB=(xB-xA)2+(yB-yA)2=02+02=0
Для ситуации, когда точки A и B лежат на прямой, перпендикулярной оси абсцисс:
AB=(xB-xA)2+(yB-yA)2=02+(yB-yA)2=yB-yA
Для случая, когда точки A и B лежат на прямой, перпендикулярной оси ординат:
AB=(xB-xA)2+(yB-yA)2=(xB-xA)2+02=xB-xA
Расстояние между точками в пространстве
Исходные данные: прямоугольная система координат Oxyz с лежащими на ней произвольными точками с заданными координатами A(xA, yA, zA) и B(xB, yB, zB) . Необходимо определить расстояние между этими точками.
Рассмотрим общий случай, когда точки A и B не лежат в плоскости, параллельной одной из координатных плоскостей. Проведем через точки A и B плоскости, перпендикулярные координатным осям, и получим соответствующие точки проекций: Ax, Ay, Az, Bx, By, Bz
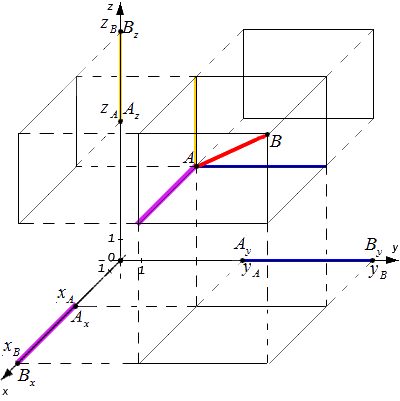
Расстояние между точками A и B являет собой диагональ полученного в результате построения параллелепипеда. Согласно построению измерения этого параллелепипеда: AxBx, AyBy и AzBz
Из курса геометрии известно, что квадрат диагонали параллелепипеда равен сумме квадратов его измерений. Исходя из этого утверждения получим равенство: AB2=AxBx2+AyBy2+AzBz2
Используя полученные ранее выводы, запишем следующее:
AxBx=xB-xA, AyBy=yB-yA, AzBz=zB-zA
Преобразуем выражение:
AB2=AxBx2+AyBy2+AzBz2=xB-xA2+yB-yA2+zB-zA2==(xB-xA)2+(yB-yA)2+zB-zA2
Итоговая формула для определения расстояния между точками в пространстве будет выглядеть следующим образом:
AB=xB-xA2+yB-yA2+(zB-zA)2
Полученная формула действительна также для случаев, когда:
– точки совпадают;
– лежат на одной координатной оси или прямой, параллельной одной из координатных осей.
Примеры решения задач на нахождение расстояния между точками
Исходные данные: задана координатная прямая и точки, лежащие на ней с заданными координатами A(1-2) и B(11+2) . Необходимо найти расстояние от точки начала отсчета O до точки A и между точками A и B.
Решение
- Расстояние от точки начала отсчета до точки равно модулю координаты этой точки, соответственно OA=1-2=2-1
- Расстояние между точками A и B определим как модуль разности координат этих точек: AB=11+2-(1-2)=10+22
Ответ: OA=2-1, AB=10+22
Исходные данные: задана прямоугольная система координат и две точки, лежащие на ней A(1, -1) и B (λ+1, 3) . λ – некоторое действительное число. Необходимо найти все значения этого числа, при которых расстояние АВ будет равно 5.
Решение
Чтобы найти расстояние между точками A и B, необходимо использовать формулу AB=(xB-xA)2+yB-yA2
Подставив реальные значения координат, получим:AB=(λ+1-1)2+(3-(-1))2=λ2+16
А также используем имеющееся условие, что АВ=5 и тогда будет верным равенство:
λ2+16=5λ2+16=25λ=±3
Ответ: АВ = 5, если λ=±3 .
Исходные данные: задано трехмерное пространство в прямоугольной системе координат Oxyz и лежащие в нем точки A (1, 2, 3) и B-7, -2, 4 .
Решение
Для решения задачи используем формулу AB=xB-xA2+yB-yA2+(zB-zA)2
Подставив реальные значения, получим: AB=(-7-1)2+(-2-2)2+(4-3)2=81=9
Ответ: |АВ| = 9
 Задачи на движение (скорость, время и расстояние) являются одной из основных типов задач по математике, которые должен уметь решать каждый школьник. В данной статье рассмотрены все типы задач на движение:
Задачи на движение (скорость, время и расстояние) являются одной из основных типов задач по математике, которые должен уметь решать каждый школьник. В данной статье рассмотрены все типы задач на движение:
— простые задачи на скорость, время и расстояние;
— задачи на встречное и противоположное движение;
— задачи на движение в одном направлении (на сближение и удаление);
— решение задач на движение по реке.
Скорость, время и расстояние: определения, обозначения, формулы
скорость = расстояние: время — формула нахождения скорости;
время = расстояние: скорость — формула нахождения времени;
расстояние = скорость · время — формула нахождения расстояния.
Скорость – это расстояние, пройденное за единицу времени: за 1 секунду, за 1 минуту, за 1 час и так далее.
Пример обозначения: 7 км/ч (читается: семь километров в час).
Если весь путь проходится с одинаковой скоростью, то такое движение называется равномерным.
На сайте представлены калькуляторы онлайн, с помощью которых можно перевести скорость, время и расстояние в другие единицы измерения:
1.Конвертер единиц измерения скорости
2.Конвертер единиц измерения времени
3.Конвертер единиц измерения расстояния (длины)
Примеры простых задач.
Задача 1.
Автомобиль проехал 180 км за 2 часа. Чему равна скорость автомобиля?
Решение: 180:2=90 (км/ч.)
Ответ: Скорость автомобиля равна 90 км/ч.
Задача 2.
Автобус проехал путь в 240 км со скоростью 80 км/ч. Сколько времени ехал автобус?
Решение: 240:80=3 (ч.)
Ответ: Автобус проехал 3 часа.
Задача 3.
Грузовик ехал 5 часов со скоростью 70 км/ч. Какое расстояние проехал грузовик за это время?
Решение: 70 · 3 = 350 (км)
Ответ: Грузовик за 5 часов проехал 350 км.
Задачи на встречное движение
В таких задачах два объекта движутся навстречу друг другу.
Задачи на встречное движение можно решать двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость сближения объектов (как сумму их скоростей), общие время и расстояние. Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
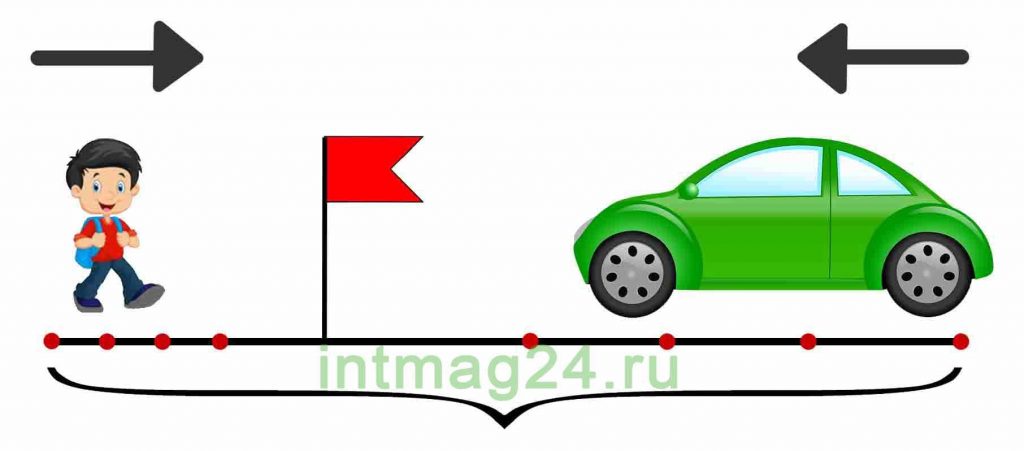
Задача 4.
Из двух пунктов навстречу друг другу одновременно выехали два поезда и встретились через 3 часа. Первый поезд ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. На каком расстоянии друг от друга находятся пункты?
Решение:
Первый способ. Найти расстояние, которое проехал каждый автобус, и сложить полученные данные:
80*3=240 (км) – проехал 1й автобус, 70*3=210 (км) – проехал 2й поезд,
240+210=450 (км) – проехали два поезда.
Второй способ. Найти скорость сближения поездов, то есть на сколько сокращалось расстояние между ними каждый час; а затем найти расстояние:
80+70=150 (км/ч), 150*3=450 (км).
Ответ: города находятся на расстоянии 450 км.
Задача 5.
Из двух городов навстречу друг другу одновременно выехали два автобуса. Первый автобус ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. Какое расстояние будет между ними через 2 часа, если расстояние между городами 450 км?
Решение:
Первый способ. Определить, сколько километров проехал каждый автобус и найти расстояние, которое осталось проехать:
80*2=160 (км)-проехал 1й автобус, 70*2=140 (км)-проехал 2й автобус,
160+140=300 (км)-проехали два автобуса, 450-300=150 (км)-осталось проехать.
Второй способ. Найти скорость сближения автобусов и умножить ее на время в пути.
80*70=150 (км/ч) – скорость сближения; 150*2=300 (км) – проехали два автобуса; 450-300=150 (км) – осталось проехать.
Ответ: Через 2часа расстояние между автобусами будет 150 км.
Задачи на движение в противоположных направлениях
В таких задачах два объекта движутся в противоположных направлениях, отдаляясь друг от друга. В таком типе задачи используется скорость удаления. Задачи на движение в противоположных направлениях также можно решить двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость удаления объектов (как сумму их скоростей), общие время и расстояние. Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
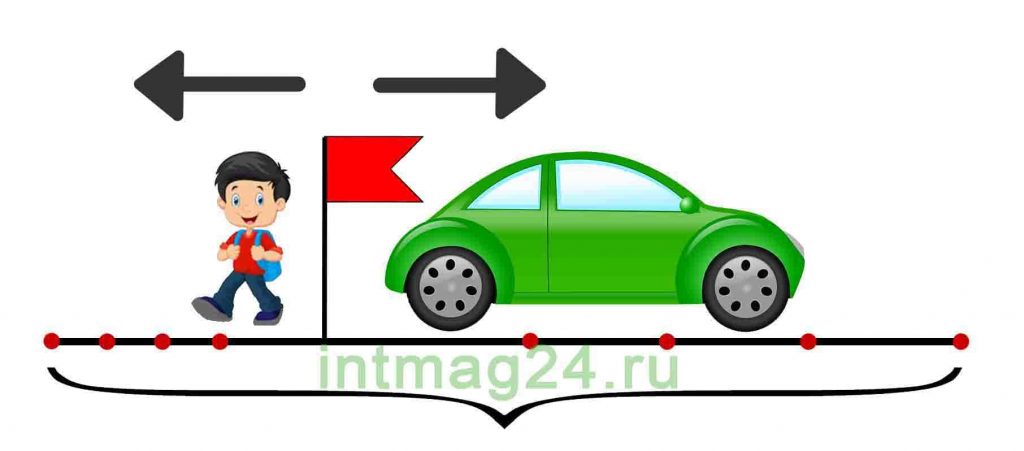
Задача 6.
Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля 100 км/ч, скорость второго – 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
Решение:
Первый способ. Определить расстояние, которое проехал каждый автомобиль и найти сумму полученных результатов:
1) 100 · 4 = 400 (км) – проехал первый автомобиль
2) 70 · 4 = 280 (км) – проехал второй автомобиль
400 + 280 = 680 (км)
Второй способ. Найти скорость удаления, то есть значение увеличения расстояния между автомобилями за каждый час, а затем скорость удаления умножить на время в пути.
100 + 70= 170 км/ч – это скорость удаления автомобилей.
170 · 4 = 680 (км)
Ответ: Через 4 часа между автомобилями будет 680 км.
Задача 7.
Из двух населённых пунктов, расстояние между которыми 40 км, вышли в противоположных направлениях два туриста. Первый турист шёл со скоростью 4 км/ч, а второй — 5 км/ч. Какое расстояние между туристами будет через 5 часов?
Решение:
Первый способ. Определить сколько километров прошёл каждый из туристов за 5 часов, сложить полученные результаты, а затем к полученному расстоянию прибавить расстояние между населенными пунктами.
1) 4 · 5 = 20 (км) – прошёл первый турист;
2) 5 · 5 = 25 (км) – прошёл второй турист;
3) 20 + 25 = 45 (км);
4) 45 + 40 = 85 (км).
Второй способ. Найти скорость удаления пешеходов, затем найти пройденное расстояние, к полученному результату прибавить расстоянием между населёнными пунктами.
4 + 5 = 9 (км/ч);
9 · 5 = 45 (км);
45 + 40 = 85 (км);
Ответ: Через 5 часов расстояние между пешеходами будет 85 км.
Задачи на движение в одном направлении
В таких задачах два объекта движутся в одном направлении с разной скоростью, при этом они сближаются друг с другом или отдаляются друг от друга. Соответственно находится скорость сближения или скорость удаления объектов.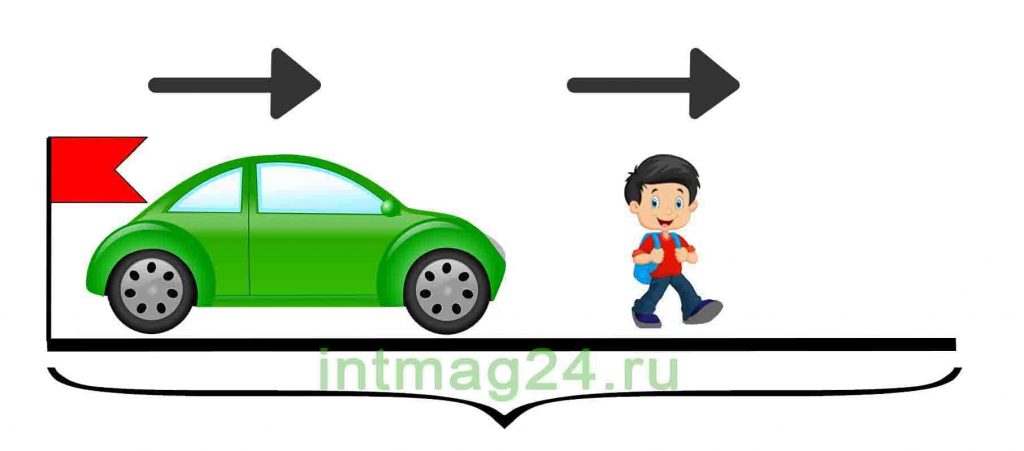
Формула нахождения скорости сближения или удаления двух объектов, которые движутся в одном направлении: из большей скорости вычесть меньшую.
Задача 8.
Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?,
Решение:
Задачу можно решить с помощью уравнения.
В этом случае скорость первого автомобиля 40 км/час, время в пути на 4 часа больше, чем время второго автомобиля (или t+4). Скорость второго автомобиля 60 км/час, время в пути – t. Расстояние оба автомобиля проехали одинаковое. Поэтому можно составить уравнение: 40*(t+4)=60*t. Отсюда получаем t=8 (часов) – время в пути второго автомобиля, за которое он догонит первый.
Решение задачи без использования уравнения.
Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на: 40 · 4 = 160 (км).
Второй автомобиль движется быстрее первого, значит, каждый час расстояние между автомобилями будет сокращаться на разность их скоростей: 60 — 40 = 20 (км/ч) – это скорость сближения.
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся: 160 : 20 = 8 (ч)
Ответ: Второй автомобиль догонит первый через 8 часов.
Задача 9.
Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов: 5 — 4 = 1 (км/ч).
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого: 5 : 1 = 5 (ч)
Ответ: Через 5 часов второй пешеход догонит первого.
Задача 10.
Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго – 40 км/ч.
1) Чему равна скорость удаления между автомобилями?
2) Какое расстояние будет между автомобилями через 3 часа?
3) Через сколько часов расстояние между ними будет 200 км?
Решение:
1) 80 — 40 = 40 (км/ч) — скорость удаления автомобилей друг от друга.
2) 40 · 3 = 120 (км) – расстояние между ними через 3 часа./
3) 200 : 40 = 5 (ч) – время, через которое расстояние между автомобилями станет 200 км.
Ответ:
1) Скорость удаления между автомобилями равна 40 км/ч.
2) Через 3 часа между автомобилями будет 120 км.
3) Через 5 часов между автомобилями будет расстояние в 200 км.
Задачи на движение по реке
Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.
Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки. Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.
Задача 11.
Лодка движется по реке. За сколько часов она преодолеет расстояние 120 км, если ее собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?
Решение:
1) лодка движется по течению реки.
27 + 3 = 30 (км/ч) – скорость лодки по течению реки.
120 : 30 = 4 (ч) – проплывет путь.
2) лодка движется против течения реки.
27 — 3 = 24 (км/ч) — скорость лодки против течения реки
120 : 24 = 5 (ч) – проплывет путь.
Ответ:
1) При движении по течению реки лодка потратит 4 часа на путь.
2) При движении против течения реки лодка потратит 5 часов на путь.
Итак, для решения задач на движение:
- Основная формула:S=ν*t;
- Нужно сделать чертеж, который поможет определить тип задачи.
- Все цифры нужно привести в единые единицы измерения: длина и время
Заключение.
Решая много задач по данной теме, ученик обязательно научится быстро ориентироваться в понятиях «скорость», «время» и «расстояние» и быстро решать задачи всех типов.
Весь курс начальной школы (за 1-4 классы) в краткой форме на сайте edu.intmag24.ru. С помощью курса можно быстро повторить основные моменты и правила по предметам: русский язык, математика, окружающий мир.
Для решения более сложных задач на движение посмотрите, как составлять схемы и таблицы данных для наглядного представления и структурирования данных.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 июля 2022 года; проверки требуют 6 правок.
Относительные размеры
объектов, lg м
-20 —
–
-18 —
–
-16 —
–
-14 —
–
-12 —
–
-10 —
–
-8 —
–
-6 —
–
-4 —
–
-2 —
–
0 —
–
2 —
–
4 —
–
6 —
–
8 —
–
10 —
–
12 —
–
14 —
–
16 —
–
18 —
–
20 —
–
22 —
–
24 —
–
26 —
–
28 —
–
30 —
←
Размер водяной капли в
тумане — 5·10-6
←
Средний радиус орбиты
Земли — 1,5·1011
Расстоя́ние, в широком смысле, степень (мера) удалённости объектов друг от друга.
Расстояние является фундаментальным понятием геометрии. Термин часто используется в других науках и дисциплинах: астрономия, география, геодезия, навигация и других. В различных дисциплинах как термин имеет различное определение, представленное ниже.
Расстояние в математике[править | править код]
Расстояние в алгебре[править | править код]
Содержание термина «расстояние» в алгебре связано с понятием метрики и метрического пространства.
Метрическим пространством называется множество X, если дано такое отображение, называемое метрикой, X² в множество неотрицательных чисел, что для любых элементов a, b, c множества X выполняются следующие аксиомы, называемые аксиомами Фреше:
1) 
2) 
3) 
Для третьей аксиомы частным случаем является неравенство треугольника.
Расстояние в множестве действительных чисел[править | править код]
Введение метрики[править | править код]
Для множества всех действительных чисел расстояние от числа a до числа b математики считают число 
Легко убедиться, что множество действительных чисел с данной метрикой будет являться метрическим пространством.
Доказательство[править | править код]
Первое условие выполняется, так как модуль любого действительного числа из определения – число неотрицательное, притом модуль числа равен нулю тогда и только тогда, когда выражение под модулем равно нулю, откуда, если равенство выполняется, то числа равны.
Второе свойство верно, так как из свойств модуля числа: 
Третье свойство выполняется, так как само свойство равносильно 

Расстояние в множестве пар действительных чисел[править | править код]
Из основных метрик в множестве пар действительных чисел (а в графической интерпретации – множестве всех точек плоскости) выделяют две: метрику Декарта и метрику Евклида.
Метрика Декарта[править | править код]
Введение метрики[править | править код]
Для множества пар действительных чисел дана метрика Декарта:

Убедимся, что множество пар действительных чисел (R²) с введенной метрикой Декарта является метрическим пространством.
Доказательство[править | править код]
Первое свойство очевидно выполняется, так как сумма модулей, каждый из которых является неотрицательным числом – также число неотрицательное. Притом равенство выполняется тогда и только тогда, когда оба выражения под модулем равны нулю, но тогда и рассматриваемые элементы-пары множества также равны.
Второе свойство выполняется, так как 
Докажем третье свойство:
Пусть даны три пары действительных чисел, (a; b), (c; d), (e; f). Тогда требуемое неравенство можно записать в следующем виде:



Метрика Евклида[править | править код]
Введение метрики[править | править код]
Для множества пар действительных чисел дана метрика Евклида:

Убедимся, что множество R² с введенной метрикой Евклида является метрическим пространством.
Доказательство[править | править код]
Первое свойство выполняется, так как арифметический корень из неотрицательного числа всегда неотрицателен. Если же выполняется равенство нулю, то оба выражения возводимые в квадрат, равны нулю, откуда требуемое очевидно.
Второе свойство выполняется, так как 
Докажем третье свойство:
Пусть даны три пары действительных чисел, (a; b), (c; d), (e; f). Тогда требуемое неравенство можно записать в следующем виде:


Расстояние в геометрии[править | править код]
В геометрии расстояние между фигурами — минимально возможная длина отрезка между точкой, принадлежащей первой фигуре, и точкой, принадлежащей второй фигуре.
Расстояние в технике[править | править код]
Расстояние между объектами — длина отрезка прямой, соединяющей два объекта. Расстояние в этом смысле является физической величиной с размерностью длины, значение расстояния выражается в единицах длины.
Расстояние в физике[править | править код]
| Расстояние | |
|---|---|
| s | |
| Единицы измерения | |
| СИ | м |
| СГС | см |
Основная статья: Длина
В физике расстояние меряется единицами длины, которые в большинстве систем измерений являются одной из основных единиц измерения. В международной системе единиц (СИ) за единицу длины принят метр. Расстоянием также называют длину пути, пройденного объектом. В этом случае производной расстояния (радиус-вектора) по времени является скорость.
Другие использования[править | править код]
В проксемике понятие расстояния используют для описания личного пространства человека.
См. также[править | править код]
- Расстояние Левенштейна
- Промежуток (математика)
- Отрезок
- Интервал
- Путь
Примечания[править | править код]
Литература[править | править код]
- Зенитное расстояние // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
С древних времен людей беспокоит мысль о достижении сверх скоростей, так же как не дают покоя раздумья о высотах, летательных аппаратах. На самом деле это два очень сильно связанных между собой понятия. То, насколько быстро можно добраться из одного пункта в другой на летательном аппарате в наше время, зависит полностью от скорости. Рассмотрим же способы и формулы расчета этого показателя, а также времени и расстояния.
Как же рассчитать скорость?
На самом деле, рассчитать ее можно несколькими способами:
- через формулу нахождения мощности;
- через дифференциальные исчисления;
- по угловым параметрам и так далее.
В этой статье рассматривается самый простой способ с самой простой формулой – нахождение значения этого параметра через расстояние и время. Кстати, в формулах дифференциального расчета также присутствуют эти показатели. Формула выглядит следующим образом:
v=S/t, где
- v – скорость объекта,
- S – расстояние, которое пройдено или должно быть пройдено объектом,
- t – время, за которое пройдено или должно быть пройдено расстояние.
Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.
Теперь нужно подставить имеющиеся значения вместо буквенных символов:
v=100 км/1,5 ч=66,66 км/ч
Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.
Таким нехитрым способом можно найти скорость через время и расстояние.
А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:
vср=(v1+v2+v3+…+vn)/n, где v1, v2, v3, vn – значения скоростей объекта на отдельных участках пути S, n – количество этих участков, vср – средняя скорость объекта на всем протяжении всего пути.
Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:
- vср=(S1+S2+…+Sn)/t, где vср – средняя скорость объекта на всем протяжении пути,
- S1, S2, Sn – отдельные неравномерные участки всего пути,
- t – общее время, за которое объект прошел все участки.
Можно записать использовать и такой вид вычислений:
- vср=S/(t1+t2+…+tn), где S – общее пройденное расстояние,
- t1, t2, tn – время прохождения отдельных участков расстояния S.
Но можно записать эту же формулу и в более точном варианте:
vср=S1/t1+S2/t2+…+Sn/tn, где S1/t1, S2/t2, Sn/tn – формулы вычисления скорости на каждом отдельном участке всего пути S.
Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.
Другие способы вычисления
Существую и другие способы и методы, которые помогают вычислить значения рассматриваемого параметра. В пример можно привести формулу вычисления мощности:
N=F*v*cos α , где N – механическая мощность,
F – сила,
v – скорость,
cos α – косинус угла между векторами силы и скорости.

Способы вычисления расстояния и времени
Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:
S=v*t, где v – понятно что такое,
S – расстояние, которое требуется найти,
t – время, за которое объект прошел это расстояние.
Таким образом вычисляется значение расстояния.
Или вычисляем значение времени, за которое пройдено расстояние:
t=S/v, где v – все та же скорость,
S – расстояние, пройденный путь,
t – время, значение которого в данном случае нужно найти.

Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.
Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.
И это еще не предел!
Видео
В нашем видео вы найдете интересные примеры решения задач на нахождение скорости, времени и расстояния.
