Как найти растояние между вершинами

В данной статье хочу рассказать вам об определённом типе задач по стереометрии, одну из которых, возможно, предстоит решить именно вам на ЕГЭ по математике. Это задачи на решение составных многогранников:

Обычно требуется найти расстояние (или квадрат расстояния) между двумя точками; какой-либо угол, либо значение одной из тригонометрических функций обозначенного в условии угла.

Для решения  необходимо знать совсем не много теории: теорему Пифагора; определения синуса, косинуса, тангенса и котангенса в прямоугольном треугольнике; значения углов тригонометрических функций.

Рассмотрим задачи:

Найдите расстояние между вершинами А и С₂  многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Результат умножьте на  корень из шести  и запишите ответ.

Соединим точки  А и С₂   и рассмотрим  прямоугольный треугольник АА₂С₂:

По теореме Пифагора:

Ответ: 6

Найдите угол САD₂ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.

Соединим точки C, А, D₂:

Рассмотрим треугольник CАD₂:  AC = CD₂ = AD₂, так как являются диагоналями квадратов со сторонами равными 8. Следовательно, треугольник CАD₂ – равносторонний, то есть все его  углы равны 60°.

Таким образом, угол CАD₂ = 60°.

Ответ: 60

Найдите квадрат расстояния между вершинами В₂ и D₃ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Соединим точки B₂, B₃ и D₃. Рассмотрим прямоугольный треугольник B₂B₃D₃:

По теореме Пифагора:

Ответ: 12

Найдите тангенс угла АBB₃ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Соединим точки В и B₃, из точки B₃ опустим перпендикуляр на ребро АВ, точку пересечения обозначим как К. Рассмотрим прямоугольный треугольник КВB₃:

Ответ: 2

Найдите квадрат расстояния между вершинами D и C₂ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Соединим точки В  и C₂, а так же C₂  и С:

Рассмотрим прямоугольный треугольник СВС₂.  По теореме Пифагора:

Ответ: 46

245376. Найдите квадрат расстояния между вершинами В₂ и D₂ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Посмотреть решение

245380. Найдите тангенс угла AВB₃ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Посмотреть решение

245382. Найдите квадрат расстояния между вершинами D и C₂ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Посмотреть решение

При решении подобных заданий главное – это «увидеть» треугольник, в который входит искомый элемент (отрезок, угол) и построить этот треугольник.  А далее уже использовать указанную в начале статьи теорию.

Есть ещё задачи с параллелепипедами:

245359   245360   245361   245362   245363

Процесс решения в них сводится к решению прямоугольного треугольника: нужно найти расстояние между вершинами (квадрат расстояния), либо заданный угол.

Мы продолжим рассматривать задачи по стереометрии? не пропустите! На этом всё. Как видите, ничего сложного. Успеха вам!

С уважением, Александр.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Сайты, меню, вход, новости

22 января 2014

Это первый урок из серии видеоуроков, посвященных задачам B13. Перед нами стандартная задача, которую часто дают на пробниках и контрольных работах. Однако решать ее мы будем весьма нестандартным методом.:)

Задача B13. Дан многогранник, изображенный на рисунке. Все двугранные углы прямые. Найдите, насколько расстояние между вершинами
A
и C2 отличается от квадрата расстояния между вершинами
E
и G1. В ответ запишите положительное число.

Для решения любых таких задач нам потребуется обобщенная теорема Пифагора. Давайте отмотаем время назад и вспомним, что такое обычная теорема Пифагора. У нас есть прямоугольный треугольник с катетами
a
,
b
и гипотенузой
c
:

В этом случае квадрат гипотенузы равен сумме квадратов катетов:

c

² =
a

² +
b

²

Теорема Пифагора в пространстве

Но все это рассматривается лишь на плоскости, потому что треугольник — это плоская фигура. Однако та же самая формула работает и в пространстве.

Теорема Пифагора в пространстве. Рассмотрим прямоугольный параллелепипед, или, просто говоря, кирпич. Такой параллелепипед однозначно задается своими сторонами
a
,
b
и
c
. Кроме того, у него есть главная диагональ. Эта диагональ соединяет наиболее удаленные точки параллелепипеда. Разумеется, если параллелепипед прямоугольный, то таких диагоналей сразу несколько, при этом все они будут равны и будут считаться по одной и той же формуле.

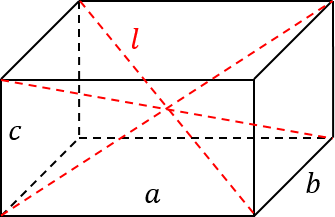
Диагональ обозначим буквой
l
. В этом случае можно записать формулу:

l

² =
a

² +
b

² +
c

²

Как связана теорема Пифагора и расстояния между точками в пространстве

Возможно, кто-то сейчас спросит: а какое отношение диагональ, тем более, в параллелепипеде имеет к нашему прямоугольному треугольнику со сторонами
a
,
b
и
c
? Отношение, на самом деле, самое прямое. Давайте достроим наш треугольник до прямоугольника, и получим, что гипотенуза
c
является диагональю на прямоугольнике.

Таким образом, перед нами, по сути, аналог теоремы Пифагора для трехмерного пространства. Давайте немножко перепишем ее:

Внимательные ученики наверняка заметят, что эта формула очень похожа на формулу расстояния в трехмерном пространстве между точками
a
и
b
. Разумеется, при условии, что точка
A
лежала бы в начале координат, а точка
B
имела координаты, равные длинам сторон нашего параллелепипеда:

A
= (0; 0; 0);

B
= (
a
,
b
,
c
).

Однако ничего удивительного в этом нет, потому что длина диагонали
l
— это как раз и есть расстояние между наиболее удаленными точками параллелепипеда.

Метод обхода точек

Но хватит теории, давайте перейдем непосредственно к нашей задаче. Итак, в первую очередь нужно найти расстояние от точки
A
до точки
C

₂. И вот для того, чтобы найти это расстояние, сейчас мы воспользуемся замечательным приемом, который называется обход точек.

Метод обхода точек заключается в следующем:

1. Построим систему координат с осями, параллельными ребрам нашего многогранника. Назовем эти оси x, y и z.
2. А теперь давайте поставим ручку в нашу точку A и попытаемся каким-то образом, двигаясь по ребрам, добраться до точки C
   ₂.

Нахождение диагонали методом обхода точек

Разумеется, последовательность осей может быть любой, решение и ответ от этого не изменится. И двигаться из одной точки в другую тоже можно по-разному. Например, можно идти к точке
B
, затем к точке
C
, затем вверх до точки
B

₂ и, наконец, двигаться вдаль — и мы попадем в точку
C

₂:

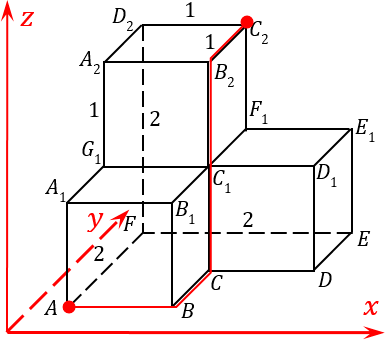
Давайте разметим, полученный нами путь:

1. Из точки A в точку B мы двигались вдоль оси x в положительном направлении. Запишем: 1x;
2. От точки B в точку C мы двигались вдоль оси игрек опять же по положительному направлению, то есть вглубь. Так и запишем 1y;
3. Затем мы шагнули на два шага вверх из точки C в точку B
   ₂. так и напишем: 2z;
4. Еще один шаг из точки B
   ₂ в точку C
   ₂ вдоль y, т. е. вглубь нашего рисунка. Запишем: 1y.

А теперь, когда мы отметили каждое звено нашей ломанной, соединяющие точки
A
и
C

₂, выпишем, сколько шагов мы получили вдоль каждой координатной оси с учетом знаков:

1. x: 1;
2. y: 1 + 1 = 2;
3. z: 2.

Теперь возвращается к нашей обобщенной теореме Пифагора и замечаем, что оси
x
,
y
и
z
— это, по сути,
a
,
b
и
c
, т. е. длины сторон параллелепипеда. Следовательно, мы можем посчитать длину диагонали этого параллелепипеда:

Вот и все! Мы получили расстояние от точки
A
до
C

₂, согласно рисунку нашего многогранника.

Диагональ параллелепипеда не зависит от маршрута обхода

Однако внимательные ученики спросят: а что будет, если мы пойдем по другому пути? Ведь от точки
A
до точки
C

₂ можно идти и другим путем: сначала вверх до точки
A
₁, затем вглубь до точки
G

₁, затем вверх до точки
A

₂, затем снова в глубину до точки
D

₂, и, наконец вправо до точки
C

₂:

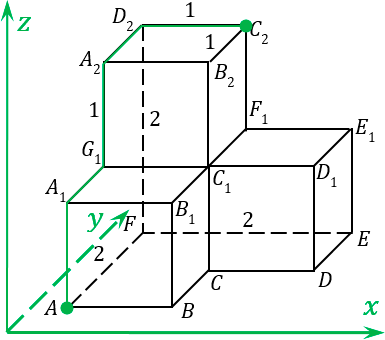
Получили совсем другой маршрут, и возникает логичный вопрос: не будет длина на этом маршруте иметь совсем другое значение координат
x
,
y
и
z
, и, соответственно, другое значение
l
? Давайте проверим.

Размечаем наш второй маршрут:

1. из точки A в точку A
   ₁ мы попадаем, смещением оси z на единичку: 1z;
2. из точки A
   ₁ в точку G
   ₁ мы попадаем, смещением по y на единичку: 1y;
3. из точки G
   ₁ в точку A
   ₂ — смещение по z: 1z;
4. из точки A
   ₂ в точку D
   ₂ — смещение по y: 1y;
5. от D
   ₂ до C
   ₂ — смещение вправо, т.е. в положительную сторону по x: 1x.

Выписываем полученные смещения:

1. x: 1
2. y: 1 + 1 = 2
3. z: 1 + 1 = 2

Итого выражение для диагонали
l
получилось в точности тем же самым:

Таким образом, мы убедились, что итоговое значение величины
l
, т. е. расстояние между точками
A
и
C

₂ не зависит от того, каким маршрутом мы будем идти из одной точки в другую. Следовательно, при решении реальных задач вы вправе выбрать любой маршрут, который будет удобен именно вам. И вообще, тот факт, что расстояние между двумя точками не зависит от того, как это расстояние мерить, на самом деле вполне логичен. Мы же занимаемся математикой, а не гаданием на кофейной гуще. Поэтому, по какому бы пути мы не пошли, ответ получится одним и тем же.

Расстояние между двумя точками в пространстве не зависит от того, как мы это расстояние считаем. Если все расчеты выполнены правильно, ответ получится одним и тем же.

Вычисление квадрата расстояния методом обхода точек

Возвращаемся к нашему заданию и переходим ко второй его части. Нужно найти расстояние между точкой
E
и точкой
G

₁. Опять предлагаю воспользоваться методом обхода точек. Начнем путь от точки
E
, будем двигаться к точке
D
, потом из точки
D
в точку
D

₁, и потом от
D

₁ напрямую в точку
G

₁:

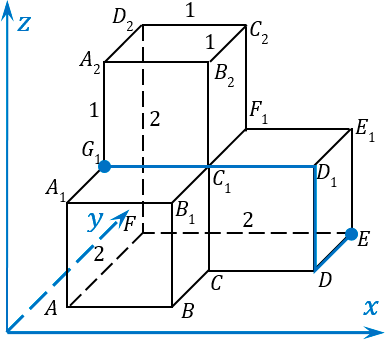
Размечаем нашу ломанную:

1. из точки E в точку D мы попадаем смещением по оси y на единицу в сторону, противоположную положительному направлению оси: -1y;
2. затем мы поднимаемся вверх на одну единицу по оси z, т. е. этот отрезок ломанной обозначаем как 1z;
3. потом мы смещаемся влево из точки D
   ₁ в точку G
   ₁ на две единицы вдоль оси x и получаем -2x.

Давайте запишем, что у нас получилось:

1. x: -2
2. y: -1
3. z: 1

По каждой из осей зафиксировано лишь одно смещение, ничего складывать, как в предыдущих случаях, не надо. Просто находим длину отрезка, соединяющего точки
E
и
G

₁. Давайте назовем этот отрезок
l

₂. Его длина равна:

Окончательное решение задачи B13

Вспоминаем, что от нас требуется найти в условии задачи. А от нас требуется квадрат расстояния между этими вершинами. Следовательно, нам нужна величина:

l

₂
² = 6

При произведении в квадрат корень исчезает.

Внимательно читайте условие задачи. Недостаточно просто найти длину отрезка или значение переменной — нужно предъявить именно ту величину, которую у нас спрашивают.

Осталось найти ту самую разницу, которую от нас требуют найти в условии задачи. Назовем ее ∆:

∆ = 6 − 3 = 3

Вот мы и нашли ответ — он равен 3.

Ключевой прием — обход точек

Еще раз — ключевая идея решения всей этой задачи. Она состоит в том, чтобы прямо на рисунке начертить путь из одной искомой точки в другую и посмотреть: вдоль каких координатных осей выполняется смещение и насколько. Затем мы выписываем эти смещения и считаем общее расстояние по обобщенной теореме Пифагора.

При этом возникает замечательный эффект: итоговое расстояние, которое мы считаем, не зависит от того, какой маршрут обхода мы выберем. В любом случае, как бы мы ни шли из одной точки в другую, расстояние получится одним и тем же. Разумеется, при условии, что все вычисления будут выполнены верно.

Аналогичным образом мы считаем второе расстояние. Пусть вас совершенно не смущает, что тут получаются отрицательные координаты, потому что при возведении в квадрат минусы сжигаются. Наконец, остается сосчитать ту самую разницу, которую требуется найти в условии задачи. Тут вообще все очень просто, и никаких дополнительных пояснений не требуется.

Краткая сводка по задачам B13

Итак, мы решили задачу B13 мы будем методом обхода точек. Давайте еще раз посмотрим, из каких шагов состояло наше решение:

1. Добавить к рисунку оси координат, параллельные ребрам многогранника;
2. Начертить «траекторию движения» от одной точки до другой, двигаясь исключительно по ребрам исходного многогранника;
3. Выяснить, вдоль какой оси происходит смещение на каждом отрезке полученной ломаной, и посчитать общее смещение;
4. Найти итоговое расстояние по обобщенной теореме Пифагора: l
   ² = a
   ² + b
   ² + c
   ², где a, b, c — суммарные смещения вдоль каждой из осей.

Но что будет, если выбрать другой маршрут? Не случится ли так, что при этом возникнут другие суммарные смещения и, следовательно, другое расстояние? Спешу вас обрадовать: суммарные смещения и расстояние между точками не зависит от выбранного маршрута. Мы убедились в этом лично, когда рассмотрели альтернативный маршрут обхода.

В общем, чертите путь так, как вам удобно — ответ всегда будет одним и тем же. В этом и состоит прелесть метода обхода точек.

Смотрите также:

1. Обход точек в стереометрии — 2
2. Разбор задачи 8 из ЕГЭ на площадь полной поверхности призмы/параллелепипеда.
3. Решение ЕГЭ-2011: вариант 1, часть B
4. Метод коэффициентов, часть 1
5. Задача B5: площадь сектора
6. Решение задач на движение по воде

From Wikipedia, the free encyclopedia

“Geodesic distance” redirects here. For distances on the surface of a sphere, see Great-circle distance. For distances on the surface of the Earth, see Geodesics on an ellipsoid. For geodesics in differential geometry, see Geodesic.

In the mathematical field of graph theory, the distance between two vertices in a graph is the number of edges in a shortest path (also called a graph geodesic) connecting them. This is also known as the geodesic distance or shortest-path distance.^[1] Notice that there may be more than one shortest path between two vertices.^[2] If there is no path connecting the two vertices, i.e., if they belong to different connected components, then conventionally the distance is defined as infinite.

In the case of a directed graph the distance d(u,v) between two vertices u and v is defined as the length of a shortest directed path from u to v consisting of arcs, provided at least one such path exists.^[3] Notice that, in contrast with the case of undirected graphs, d(u,v) does not necessarily coincide with d(v,u)—so it is just a quasi-metric, and it might be the case that one is defined while the other is not.

[edit]

A metric space defined over a set of points in terms of distances in a graph defined over the set is called a graph metric.
The vertex set (of an undirected graph) and the distance function form a metric space, if and only if the graph is connected.

The eccentricity ϵ(v) of a vertex v is the greatest distance between v and any other vertex; in symbols,

It can be thought of as how far a node is from the node most distant from it in the graph.

The radius r of a graph is the minimum eccentricity of any vertex or, in symbols,

The diameter d of a graph is the maximum eccentricity of any vertex in the graph. That is, d is the greatest distance between any pair of vertices or, alternatively,

To find the diameter of a graph, first find the shortest path between each pair of vertices. The greatest length of any of these paths is the diameter of the graph.

A central vertex in a graph of radius r is one whose eccentricity is r—that is, a vertex whose distance from its furthest vertex is equal to the radius, equivalently, a vertex v such that ϵ(v) = r.

A peripheral vertex in a graph of diameter d is one whose eccentricity is d—that is, a vertex whose distance from its furthest vertex is equal to the diameter. Formally, v is peripheral if ϵ(v) = d.

A pseudo-peripheral vertex v has the property that, for any vertex u, if u is as far away from v as possible, then v is as far away from u as possible. Formally, a vertex v is pseudo-peripheral if, for each vertex u with d(u,v) = ϵ(v), it holds that ϵ(u) = ϵ(v).

A level structure of the graph, given a starting vertex, is a partition of the graph’s vertices into subsets by their distances from the starting vertex.

A geodetic graph is one for which every pair of vertices has a unique shortest path connecting them. For example, all trees are geodetic.^[4]

The weighted shortest-path distance generalises the geodesic distance to weighted graphs. In this case it is assumed that the weight of an edge represents its length or, for complex networks the cost of the interaction, and the weighted shortest-path distance d^W(u, v) is the minimum sum of weights across all the paths connecting u and v. See the shortest path problem for more details and algorithms.

Algorithm for finding pseudo-peripheral vertices[edit]

Often peripheral sparse matrix algorithms need a starting vertex with a high eccentricity. A peripheral vertex would be perfect, but is often hard to calculate. In most circumstances a pseudo-peripheral vertex can be used. A pseudo-peripheral vertex can easily be found with the following algorithm:

1. Choose a vertex .
2. Among all the vertices that are as far from as possible, let be one with minimal degree.
3. If then set and repeat with step 2, else is a pseudo-peripheral vertex.

See also[edit]

Notes[edit]

Графы имеют различные свойства, которые используются для характеристики графов в зависимости от их структуры. Эти свойства определены в конкретных терминах, относящихся к области теории графов. В этой главе мы обсудим несколько основных свойств, которые являются общими для всех графиков.

Расстояние между двумя вершинами

Это число ребер в кратчайшем пути между вершиной U и вершиной V. Если существует несколько путей, соединяющих две вершины, то кратчайший путь рассматривается как расстояние между двумя вершинами.

Обозначение – d (U, V)

Может быть любое количество путей из одной вершины в другую. Среди них вам нужно выбрать только самый короткий.

пример

Посмотрите на следующий график –

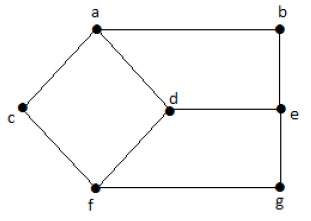
Здесь расстояние от вершины ‘d’ до вершины ‘e’ или просто ‘de’ равно 1, поскольку между ними есть одно ребро. Существует много путей от вершины ‘d’ до вершины ‘e’ –

• да, а, бе
• дф, фг, гэ
• де (считается для расстояния между вершинами)
• дф, фц, ca, ab, be
• да, ac, cf, fg, ge

Эксцентриситет вершины

Максимальное расстояние между вершиной и всеми остальными вершинами рассматривается как эксцентриситет вершины.

Обозначение – e (V)

Расстояние от конкретной вершины до всех других вершин графа берется, и среди этих расстояний эксцентриситет является наибольшим из расстояний.

пример

На приведенном выше графике эксцентриситет «а» равен 3.

Расстояние от «a» до «b» равно 1 («ab»),

от ‘a’ до ‘c’ равно 1 (‘ac’),

от «а» до «d» равно 1 («объявление»),

от ‘a’ до ‘e’ равно 2 (‘ab’ – ‘be’) или (‘ad’ – ‘de’),

от ‘a’ до ‘f’ равно 2 (‘ac’ – ‘cf’) или (‘ad’ – ‘df’),

от ‘a’ до ‘g’ равно 3 (‘ac’ – ‘cf’ – ‘fg’) или (‘ad’ – ‘df’ – ‘fg’).

Таким образом, эксцентриситет равен 3, что является максимумом от вершины «а» от расстояния между «ag», которое является максимальным.

Другими словами,

е (б) = 3

е (с) = 3

е (д) = 2

е (е) = 3

е (е) = 3

е (г) = 3

Радиус связного графа

Минимальный эксцентриситет от всех вершин рассматривается как радиус графа G. Минимальный среди всех максимальных расстояний между вершиной до всех остальных вершин рассматривается как радиус графа G.

Обозначение – r (G)

Из всех эксцентриситетов вершин графа радиус связного графа является минимумом всех этих эксцентриситетов.

Пример – На приведенном выше графике r (G) = 2, что является минимальным эксцентриситетом для «d».

Диаметр графика

Максимальный эксцентриситет от всех вершин рассматривается как диаметр графа G. Максимальный из всех расстояний между вершиной до всех других вершин рассматривается как диаметр графа G.

Обозначение – d (G)

Из всех эксцентриситетов вершин графа диаметр связного графа является максимальным из всех этих эксцентриситетов.

Пример. На приведенном выше графике d (G) = 3; что является максимальным эксцентриситетом.

Центральная точка

Если эксцентриситет графа равен его радиусу, то он называется центральной точкой графа. Если

e (V) = r (V),

тогда «V» является центральной точкой графа «G».

Пример – в примере графика ‘d’ является центральной точкой графика.

e (d) = r (d) = 2

Центр

Множество всех центральных точек «G» называется центром графа.

Пример. В примере графика {‘d’} является центром графика.

Длина окружности

Число ребер в самом длинном цикле «G» называется окружностью «G».

Пример. На графике примера длина окружности равна 6, что мы получили из самого длинного цикла acfgeba или acfdeba.

обхват

Число ребер в кратчайшем цикле G называется его обхват.

Обозначения – g (G).

Пример – в примере графика обхват графа равен 4, который мы получили из кратчайшего цикла acfda или dfged или abeda.

Теорема о сумме степеней вершин

Если G = (V, E) ненаправленный граф с вершинами V = {V ₁ , V ₂ ,… V _n }, то

n ∑ i = 1 градус (V _i ) = 2 | E |

Следствие 1

Если G = (V, E) ориентированный граф с вершинами V = {V ₁ , V ₂ ,… V _n }, то

n ∑ i = 1 градус ⁺ (V _i ) = | E | = n ∑ i = 1 град ^– (V _i )

Следствие 2

В любом неориентированном графе число вершин с нечетной степенью является четным.

Следствие 3

В неориентированном графе, если степень каждой вершины равна k, то

к | V | = 2 | E |

Следствие 4

В неориентированном графе, если степень каждой вершины не меньше k, то

к | V | ≤ 2 | E |

Следствие 5

В неориентированном графе, если степень каждой вершины не более k, то

к | V | ≥ 2 | E |