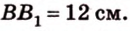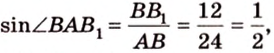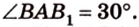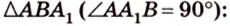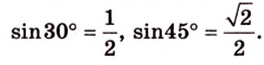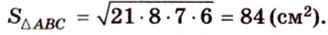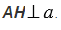Содержание:
В планиметрии угол – это геометрическая фигура, образованная двумя лучами, которые выходят из одной точки – вершины угла (лучи – стороны угла). Такое определение понятия угла переносится и в стереометрию. Углы в пространстве рассматриваются между двумя прямыми, прямой и плоскостью, двумя плоскостями. Опишем и определим каждый из этих случаев.
Угол между двумя прямыми в пространстве
Две прямые, лежащие в одной плоскости, при пересечении образуют смежные и вертикальные углы. В модуле 1 мы повторили все свойства таких углов (вертикальные углы равны, а смежные – дополняют друг друга до 180°). В пространстве (аналогично планиметрии) также сохраняются все названия и понятия об углах и их величинах. Меньший из углов, образованных двумя пересекающимися прямыми, называют углом между прямыми. Угол между перпендикулярными прямыми равен 90°. Считают, что параллельные прямые также образуют угол, равный 0°. В стереометрии рассматривают угол между скрещивающимися прямыми. Пусть даны скрещивающиеся прямые
Углом между скрещивающимися прямыми называется угол между прямыми, которые пересекаются и соответственно параллельны скрещивающимся. 
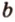
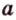
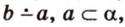
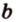
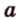
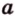
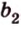
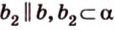
Итак,
Если 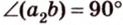
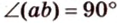
Угол между прямой и плоскостью в пространстве
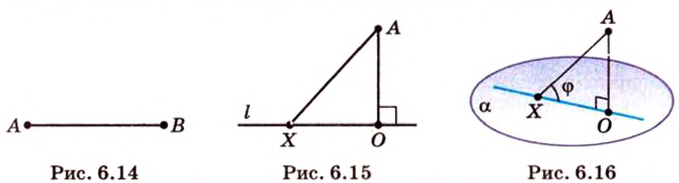
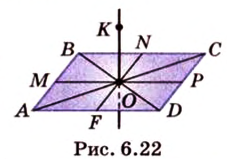
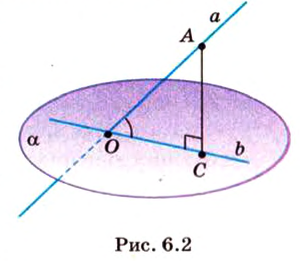
Об угле наклона прямой к плоскости говорят в том случае, когда прямая пересекает эту плоскость. Чтобы построить, например, угол между прямой 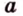
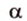
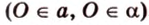
- выбирают точку
прямой
;
- проводят из точки
перпендикуляр к плоскости
;
- проводят через точки плоскости
и
прямую
.
Прямую 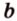
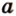
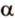
Углом между прямой и плоскостью называется угол между этой прямой и ее проекцией на плоскость. Если прямая 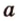
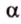
Угол между прямой 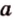
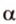
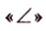
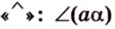
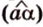
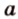
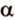
Угол между двумя плоскостями, пространства
Прямая на плоскости разбивает ее на две полуплоскости. Две полуплоскости могут иметь общую прямую и не образовывать одну плоскость. В этом случае они образуют фигуру, которую называют двугранным углом.
Двугранным углом называется фигура, образованная двумя полуплоскостями вместе с общей прямой, их ограничивающей. Эту прямую называют ребром двугранного угла.
Если двугранный угол пересечь плоскостью, перпендикулярной его ребру, то лучи, по которым она пересекает заданные
полуплоскости, образуют линейный угол, например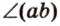
Пересекающиеся плоскости образуют четыре угла. Чтобы определить угол между двумя плоскостями, проводят плоскость, перпендикулярную прямой их пересечения. Она пересекает данные плоскости по двум прямым. Угол между этими прямыми называется углом между данными плоскостями. Т.е. угол между двумя пересекающимися плоскостями – это угол между двумя прямыми, которые принадлежат этим плоскостям и перпендикулярны прямой их пересечения.
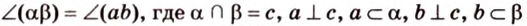
Если линейный угол – 90°, то плоскости перпендикулярны. Если плоскости параллельны, то угол между ними равен 0°.
Теорема 1
Угол между плоскостями не зависит от места построения линейного угла.
Доказательство:
Выберем точки 
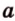
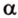
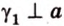
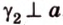
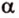
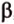
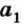
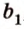
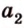
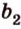
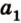
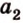
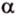
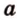
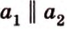
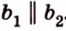
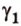
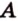
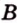
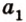
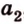
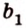
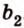
Пример №1
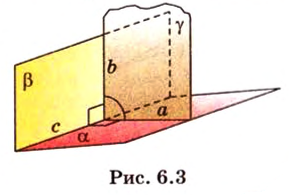
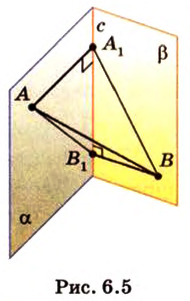
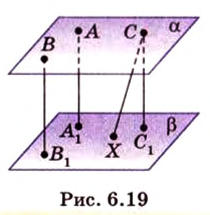
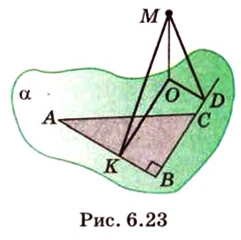
Концы отрезка длиной 24 см принадлежат двум перпендикулярным плоскостям. Расстояния от концов отрезка до линии пересечения данных плоскостей равны 12 см и 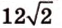
Дано: 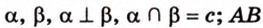

Найти: углы, образованные отрезком 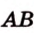
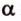
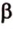
Решение:
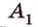
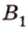
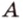
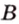
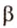
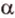
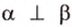
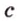
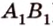
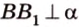
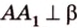
Итак, 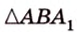
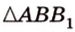
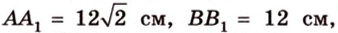
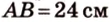
Из 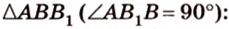
Из 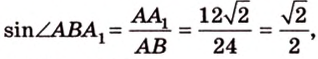
Ответ. 30°; 45°.
Почему именно так?
В этой задаче важно построить проекции концов отрезка на другую, перпендикулярную ей, плоскость. При этом следует помнить, что они должны лежать на прямой пересечения данных перпендикулярных плоскостей, согласно свойствам перпендикулярных плоскостей. Далее, рассматривая прямоугольные треугольники, нужно правильно использовать определение синуса угла как отношения противолежащего катета к гипотенузе и таблицу значений:
Расстояния в пространстве
Одним из ключевых понятий геометрии является длина отрезка. Через него вводится много других понятий, связанных с понятием расстояния. Как известно, расстоянием между двумя точками 
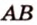
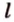
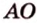
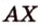
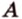
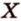
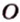
Рассмотрим плоскость 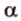
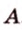
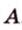
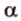
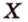
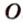
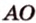
Итак, расстояние от точки до плоскости равно длине перпендикуляра, проведенного из этой точки к плоскости.
Если точка принадлежит плоскости, то в этом случае расстояние от нее до плоскости равно нулю.
Расстояние от точки 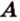
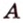
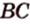
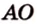
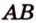

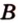
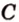
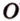
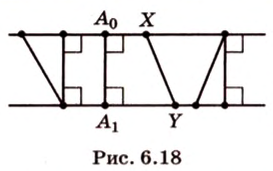
Расстояние между двумя параллельными прямыми равно длине общего перпендикуляра этих прямых (рис. 6.18). Это вытекает из того, что все такие перпендикуляры 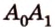
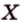
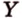
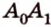
Теорема 2 (о расстоянии между параллельными прямой и плоскостью)
Расстояние между параллельными прямой и плоскостью равно длине общего перпендикуляра, проведенного из произвольной точки прямой к плоскости.
Данная теорема доказывается рассуждениями, аналогичными приведенным выше, о расстоянии между параллельными прямыми.
Теорема 3 (о расстоянии между параллельными плоскостями)
Расстояние между параллельными плоскостями равно длине общего перпендикуляра, проведенного из произвольной точки одной плоскости ко второй.
Доказательство:
Пусть имеем две параллельные плоскости 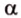
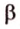
и второй, то перпендикуляр 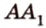
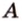
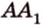
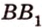
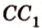
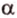
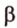
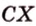
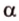
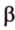
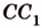
А это вытекает из того, что перпендикуляр 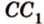
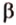
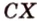
Понятие расстояния между точками широко применяется в разнообразных сферах жизни человека – от науки до быта и досуга. Используется оно в тех случаях, когда размерами реальных объектов, расстояние между которыми вычисляется, в данных условиях можно пренебречь. Так мы говорим о расстоянии между звездами, планетами, передатчиками и принима-телями информации, населенными пунктами, ядрами атома и электронами на его орбите и т.п.
Расстояние между скрещивающимися прямыми
Сначала рассмотрим определение перпендикуляра, проведенного к двум скрещивающимся прямым, и докажем его существование и единственность.
Общим перпендикуляром к двум скрещивающимся прямым называется отрезок с концами на этих прямых, перпендикулярный каждой из них.
Теорема 4
Две скрещивающиеся прямые имеют общий перпендикуляр, и притом только один. Он является общим перпендикуляром к параллельным плоскостям, проходящим через эти прямые.
Доказательство:
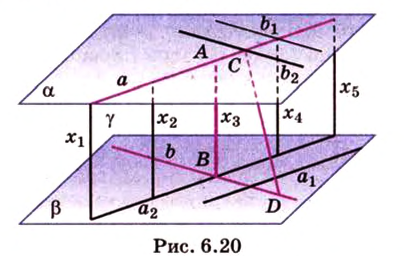
Действительно, пусть 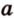
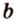
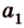
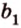
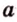
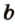
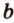
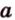
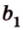
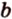
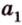
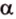
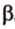
Плоскости 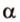
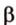
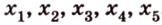
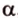
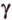
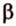
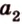
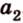
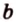
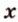
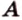
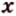
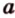
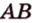
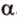
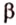
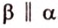
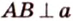
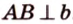
Отрезок 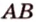
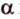
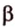
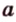
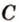
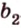
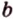

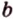
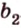
Поскольку она перпендикулярна прямым 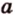
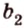

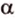




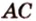
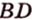
Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра.
Пример №2
Отрезок 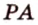
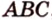
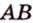
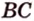
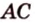
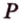
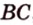
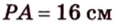
Решение:
Пусть 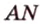
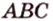
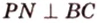
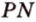
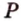
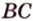
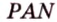
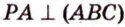
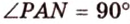
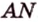
Из формулы для площади треугольника 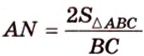
Необходимую площадь определим по формуле Герона:
Тогда 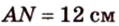
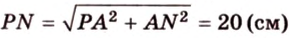
Ответ. 20 см.
Пример №3
Прямая 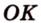
Доказательство:
Пусть 
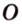
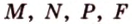
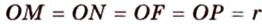
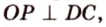
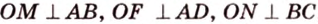
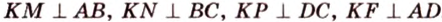
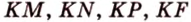
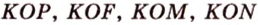
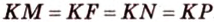
Пример №4
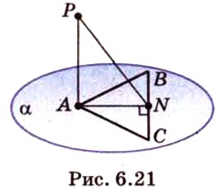
Точка 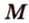
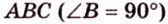
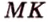
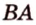
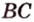
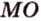
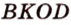
Доказательство:
Поскольку отрезки 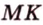
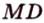
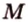
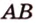
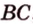
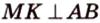
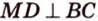
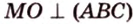
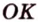
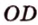
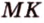
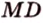
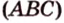
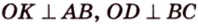
- Подобие треугольников
- Решение прямоугольных треугольников
- Параллелограмм
- Теорема синусов и теорема косинусов
- Квадрат и его свойства
- Трапеция и ее свойства
- Площадь трапеции
- Центральные и вписанные углы
Как найти длину перпендикуляра
Даны точка и прямая представленная уравнением (1) § 161. Требуется найти расстояние от точки до прямой т. е. длину перпендикуляра (см. рис. 175), опущенного из точки на прямую .
Можно сначала найти основание К перпендикуляра (§ 161, пример), затем длину отрезка Проще применить формулу (при обозначениях § 161)
т. е. в векторной форме
Числитель выражения (1а) есть площадь параллелограмма (§ 111) , а знаменатель — длина основания Следовательно, дробь равна высоте параллелограмма.
Расстояние от точки до прямой
Что называется расстоянием от точки до прямой? Как найти расстояние от точки до прямой?
Расстоянием от точки до прямой называется длина перпендикуляра, опущенного из данной точки на прямую.
Таким образом, чтобы найти расстояние от точки до прямой, надо из точки к прямой провести перпендикуляр и найти его длину.
Например, на рисунке 1 расстояние от точки A до прямой a равно длине перпендикуляра AB, опущенного из точки A на прямую a.
Задачи на нахождение расстояния от точки до прямой сводятся к рассмотрению прямоугольного треугольника.
№ 1. Из точки к прямой проведены две наклонные, длины которых относятся как 2:3, а длины их проекций соответственно равны 2 см и 7 см. Найти расстояние от точки до прямой.

BC и BD — их проекции, BC=2 см, BD=7 см
1) Пусть k — коэффициент пропорциональности. Тогда AC=2k см, AD=3k см.
2) Рассмотрим треугольник ABC — прямоугольный (так как AB — перпендикуляр к прямой a по условию). По теореме Пифагора
3) Аналогично, из треугольника ABD
4) Приравниваем правые части полученных равенств и находим k:
5) Зная k, найдем AB:
№ 2. Из точки к прямой проведены две наклонные, длины которых равны 13 см и 15 см. Найти расстояние от точки до прямой, если разность проекций наклонных равна 4 см.

AC и AD — наклонные, AC=13 см, AD=15 см,
BC и BD — их проекции, BD-BC=4 см
1) Пусть BC=x см, тогда BD=x+4 см.
2) Рассмотрим треугольник ABC — прямоугольный (так как AB — перпендикуляр к прямой a по условию). По теореме Пифагора
3) Аналогично, из треугольника ABD
4) Приравниваем правые части полученных равенств и находим x:
5) Зная x, найдем AB:
№ 3. Найти расстояние от точки A до прямой a, если известно, что наклонная AF, длина которой равна c, образует с прямой a угол α.

Треугольник ABF — прямоугольный (так как AB — перпендикуляр к прямой a по условию). AB — катет, противолежащий углу ACB, AF — гипотенуза.
Основные сведения о перпендикуляре к прямой — что это такое, как находить
Каким будет определение положения прямой и плоскости, зависит от наличия общих точек. Если их больше одной, то прямая лежит на данной плоскости, если одна — то она ее пересекает. Если прямая не имеет с плоскостью точек пересечения, то прямая и плоскость параллельны.
Пересечение прямой линии и плоскости может происходить под разными углами. Если при пересечении между прямой и плоскостью образуется прямой угол, то такая прямая является к плоскости перпендикуляром. При этом она перпендикулярна всем прямым линиям, принадлежащим данной плоскости. Из этого свойства вытекает следующее определение.
Перпендикулярной к плоскости называется прямая линия, которая перпендикулярна всем без исключения прямым, лежащим в выбранной плоскости.
Следствием из данного определения является свойство плоскости, для которой установлено наличие перпендикуляра. Оно формулируется следующим образом: «Если плоскость перпендикулярна некоторой прямой, то она является также перпендикулярной для всех прямых, параллельных данной прямой».
В решении задач на построение перпендикуляров к плоскости в конкретной точке существует только одно решение, поскольку через определенную точку можно провести только одну прямую, занимающую по отношению к плоскости перпендикулярное положение.
О единственности такой прямой в геометрии существует доказательство.
Проведение перпендикуляра из точки к прямой
В жизни с перпендикуляром можно столкнуться часто. Например, если по двум параллельным направляющим движутся тела, то кратчайшее расстояние между ними будет лежать именно по перпендикуляру.
Допустим, на уроке ученикам дали задание построить перпендикуляр к имеющейся площади. Особым условием является то, что проходить этот перпендикуляр должен через выбранную точку. Технически задача проста. Для ее исполнения нужен чертежный треугольник, один угол у которого является прямым, то есть составляет 90°.
Приложив его к прямой таким образом, что одна из сторон, образующих прямой угол, лежит на прямой, а другая — проходит через точку с определенными координатами, необходимо соединить эту точку и прямую.
Такой отрезок будет кратчайшим соединением точки с прямой линией (и выбранной плоскостью).
Взаимное положение такого перпендикуляра и прямой обозначается специальным знаком.
Для перпендикуляра, проведенного из выбранной точки к прямой, можно определить длину. Она равна расстоянию от этой точки до точки пересечения с прямой плоскостью.
Как построить перпендикуляр к прямой
Построить перпендикуляр к прямой можно несколькими способами:
1. С помощью циркуля.
Из выбранной точки P проводим полуокружность, которая пересекается с прямой в точках A и B.
Затем тем же радиусом строим две окружности, центры которых совпадают с точками A и B. При этом окружности проходят через точку P.
Следующим шагом будет соединение точек P и Q.
На данном рисунке перпендикуляр к прямой AB — отрезок PQ.
2. Вторым способом построения перпендикуляра является использование транспортира. Чтобы провести перпендикуляр, внимательно откладываем 90° от выбранной точки на прямой, используя при этом линейку транспортира. Отрезок, соединяющий эту точку и деление 90°, является перпендикуляром к прямой в заданной точке.
3. Третий способ был описан выше. Он основан на применении чертежного треугольника и линейки. С помощью линейки проводим прямую. Прикладываем к ней прямым углом треугольник и очерчиваем этот угол с двух сторон. Один отрезок совпадает с имеющейся прямой, а второй является перпендикуляром к ней.
Пояснение на примерах
В конспектах по геометрии присутствует понятие высоты, представляющей собой перпендикуляр к одной из сторон геометрической фигуры (например, треугольника).
Высотой треугольника называется перпендикуляр, который выходит из вершины треугольника и следует к противоположной стороне (либо к продолжению этой стороны, если треугольник тупоугольный).
В данном определении содержится отличие от основной характеристики биссектрисы, которая, опускаясь на противолежащую углу сторону, не является перпендикуляром к ней.
Аналогичная ситуация с определением медианы — линии, исходящей из угла треугольника и делящей противоположную сторону на две равные части.
Высоту треугольника можно провести из любого его угла, поэтому у каждого треугольника имеется три высоты.
Существует теорема, что все три высоты треугольника пересекаются в одной точке, которая называется ортоцентром.
Используя свойство высоты треугольника о пересечении одной из его сторон под прямым углом, можно через высоту выразить формулу площади треугольника:
Уравнение для расчета высоты через площадь:
Найти через длины сторон:
h a = 2 p p — a p — b p — c a
где p — это полупериметр треугольника, который рассчитывается так:
p = a + b + c 2
Можно дать краткую характеристику еще двум способам выразить высоту треугольника:
План урока:
Понятие перпендикуляра
Расстояния между плоскостями и прямыми
Теорема о трех перпендикулярах
Угол между прямой и плоскостью
Задачи на перпендикуляры, наклонные, расстояния
Понятие перпендикуляра
Пусть есть некоторая плоскость α и точка М в пространстве, не лежащая на α. Проведем через М прямую, перпендикулярную α. Она пересечет α в какой-нибудь точке К. Отрезок МК именуют перпендикуляром к плоскости α.
Если через М мы проведем ещё одну прямую, пересекающую α, то она пересечет α в какой-нибудь точке Н. В результате мы получим прямоугольный ∆МНК:
Запомним некоторые геометрические термины. В таком построении:
- отрезок МН – это наклонная;
- отрезок НК – это проекция наклонной, или просто проекция;
- К – основание перпендикуляра;
- Н – основание наклонной.
Заметим, что в ∆МНК отрезок МН – это гипотенуза, а МК – это катет. Напомним, что катет всегда меньше гипотенузы. Отсюда вытекает вывод – длина перпендикуляра всегда меньше длины наклонной (конечно, если они проведены из одной точки).
Это значит, что из всех отрезков, которыми можно соединить точку и плоскость, именно перпендикуляр будет кратчайшим. Поэтому его называют расстоянием между точкой и плоскостью.
Расстояния между плоскостями и прямыми
Докажем довольно очевидный факт:
Действительно, пусть α и β – параллельные плоскости. Выберем на α произвольные точки М и Р, а далее опустим перпендикуляры из точек М и Р на β, которые пересекут β в точках Н и К соответственно:
Так как МН и РК перпендикулярны плоскости α, то они параллельны. Но также и α||β. Тогда, по теореме 12 из этого урока, отрезки МН и РК одинаковы, ч. т. д.
Этот факт позволяет ввести понятия расстояния между параллельными плоскостями.
Уточним, что если плоскости пересекаются, то расстояние между ними не может быть определено.
Далее рассмотрим случай с плоскостью α и параллельной ей прямой m. Оказывается, и в этом случае точки прямой равноудалены от плоскости.
Действительно, отметим на m произвольную точку К. Далее через K проведем такую плоскость β, что α||β. Так как точки β равноудалены от α, то нам достаточно показать, что m будет полностью принадлежать β:
Так как m и β уже имеют общую точку K, то они m либо пересекает β, либо лежит в ней. Будем рассуждать от противного и предположим, что m и β пересекаются. Так как m||α, то в α можно построить прямую n, параллельную m. Если m пересекает β, то и nтакже должна ее пересекать (по теореме 3 из этого урока). Но если n пересекает β, то точка их пересечения будет одновременно принадлежать и β, и α. То есть у этих плоскостей будет общая точка. Но α и β параллельны и потому не могут иметь общих точек. Значит, на самом деле m и β НЕ пересекаются. Остается один вариант – m принадлежит β, ч. т. д.
Из этой теоремы вытекает понятие расстояния между прямой и плоскостью.
Уточним, что если плоскость и прямая не параллельны, то расстояние между ними определить нельзя.
Осталось понять, как определять расстояние между прямыми в пространстве. Для параллельных прямых определение расстояния известно ещё из курса планиметрии. Естественно, что для пересекающихся прямых расстояние определить невозможно. Остается только случай скрещивающихся прямых.
Пусть прямые m и n скрещиваются. Тогда через n можно построить плоскость α, параллельную m. И наоборот, через m возможно провести плоскость β, параллельную n:
Далее опустим из какой-нибудь точки m перпендикуляр на α. Обозначим этот перпендикуляр как р. Тогда через пересекающиеся прямые m и р можно провести единственную плоскость γ:
Заметим, что плоскости α и γ обязательно пересекутся по некоторой прямой m’, причем m’||m. Действительно, m’ и m не могут скрещиваться, ведь они находятся в одной плоскости γ. Не могут они и пересекаться, ведь в противном случае точка их пересечения была бы общей для m и α, а они параллельны и общих точек не имеют.
Также заметим, что прямые n и m’ пересекаются, ведь они располагаются в одной плоскости α. Параллельными они быть не могут, ведь тогда по свойству транзитивности параллельности получилось бы, что и n||m, а это не так. Обозначим точку пересечения n и m’ буквой K.
Далее через K в плоскости γ проведем прямую р’, параллельную р:
Теперь начнем рассуждения. Если р⊥α, то также р⊥m’. Так как р’||р, то и р’⊥m’, ведь прямая, перпендикулярная одной из параллельных прямых, будет перпендикулярна и второй прямой. По этому же правилу из того факта, что m’||m и р’⊥m’ вытекает, что и m⊥р’. Наконец, если р⊥α, то р⊥n. Для ясности отметим все найденные нами прямые углы на рисунке:
В итоге получилось, что отрезок HK перпендикулярен и n, и m. По этой причине его называют общим перпендикуляром к прямым n и m. Именно он и считается расстоянием между скрещивающимися прямыми m и n.
Отдельно отметим, что HK – это ещё и общий перпендикуляр к α и β. Понятно, что так как р⊥α и р’||р, то и р’⊥α, то есть HK – перпендикуляр к α.
Теперь через точку H проведем прямую n’, параллельную n. Так как β||n, то n’ будет находиться в β (по теор. 6 в этом уроке).
Раз n||n’ и р’⊥n, то и р’⊥n’. Тогда получается, что в β есть сразу две пересекающихся прямых (это m и n’), которые перпендикулярны р’. Поэтому можно утверждать, что р’⊥β, то есть HK– перпендикуляр к β.
Отсюда сразу вытекает ещё один важный вывод – плоскости α и β параллельны, так как имеют общий перпендикуляр.
Итак, мы показали, что общий перпендикуляр можно построить для любых двух скрещивающихся прямых. Но можно построить ещё один такой перпендикуляр? Нельзя, и это можно показать.
Сначала заметим, что второй перпендикуляр нельзя провести через точку К, ведь в таком случае получалось бы, что к m проведены два различных перпендикуляра из одной и той же точки, что невозможно. Аналогично перпендикуляр не может проходить и через Н.
Предположим тогда, что второй перпендикуляр проходит через точки С и D, причем С находится на m, а D находится на n. То есть CD⊥m и СD⊥n:
Проведем через С прямую n’’, параллельную n. Раз СD⊥n и n||n’’, то и СD⊥n’’. При этом n’’ находится в β (это доказывается также, как и в случае с n’). Тогда получается, что в β есть две прямые, n’’ и m, каждая из которых перпендикулярна СD, и при этом n’’ и m пересекаются. Тогда CD⊥β. Из этого вытекает, что СD и HK параллельны, а потому через них можно провести плоскость δ. Этой плоскости будут принадлежать точки С, H, К и D. Но тогда в этой плоскости должны находиться прямые m и n, ведь они имеют с ней по две общих точки. Но m и n – скрещивающиеся прямые, то есть они никак не могут находиться в одной плоскости. Это противоречие означает, что второй общий перпендикуляр CD не существует.
Итак, из всех наших рассуждений мы можем сделать следующие выводы:
Теорема о трех перпендикулярах
Сформулируем важное утверждение, которое называют теоремой о трех перпендикулярах.
Проиллюстрируем теорему с помощью картинки:
Доказательство этой теоремы очень простое. Так как МК⊥α, то также МК⊥m. Теперь рассмотрим расположение плоскости МНК и прямой m. МК⊥m и HK⊥m. Тогда по признаку перпендикулярности можно утверждать, что m перпендикулярна всей плоскости HM, то есть каждой находящейся в ней прямой. В частности, m⊥HK, ч. т. д.
Оказывается, верно и обратное утверждение (так называемая обратная теорема о трех перпендикулярах):
Доказательство аналогично предыдущему. Так как m⊥MH и m⊥MK, то m⊥HMK. Отсюда вытекает, что и m⊥HK.
Угол между прямой и плоскостью
Проекция наклонной позволяет ввести такое понятие, как угол между прямой и плоскостью.
Пусть надо определить угол между прямой HM и плоскостью α:
Здесь надо просто построить перпендикуляр МК. В результате появится отрезок HK– проекция HM на α. Тогда угол между HM и HK, то есть ∠MHK, как раз и будет углом между HM и α.
Однако не всегда таким образом можно построить проекцию прямой. Проблемы возникнут, если прямая либо параллельна, либо перпендикулярна плоскости. В таких случаях используются такие правила:
Задачи на перпендикуляры, наклонные, расстояния
Рассмотрим несколько задач, в каждой из которых рассматривается куб АВСDEFGH. При этом предполагается, что ребро такого куба имеет длину, равную единице.
Задание. В кубе АВСDEFGH найдите расстояние между точкой А и гранью CDHG:
Решение. Ребро AD перпендикулярно грани DH (так как AD⊥DH и AD⊥CD). Поэтому как раз АD и является расстоянием между А и СDHG. Значит, оно равно единице.
Ответ: 1.
Примечание. Для решения следующих задач запомним, что ребро DH перпендикулярно грани АВСD. Вообще в кубе все ребра, пересекающиеся с гранями, перпендикулярны таким граням.
Задание. Найдите в кубе расстояние между вершиной А и плоскостью BDH:
Решение. Проведем на грани АВСD перпендикуляр АК из А к прямой BD:
Докажем, что АК – перпендикуляр в BDH. Для этого надо найти две прямые в BDH, перпендикулярные АК. Первая такая прямая – это BD (мы специально провели АК⊥BD). Вторая такая прямая – это DH. Действительно, DH перпендикулярна всей грани АВСD, а значит, и прямой АК.
Теперь найдем длину АК. Ее можно вычислить из прямоугольного ∆АКD. В нём ∠ADB =45°, ведь это угол между стороной квадрата АВСD и его диагональю.
Найти АК можно с помощью тригонометрии в ∆АКD:
Задание. Найдите расстояние от H до плоскости EDG:
Решение. Обозначим середину отрезка ЕD буквой М.Далее в ∆МНG опустим высоту из НК на сторону MG:
Попытаемся доказать, что HK – это перпендикуляр к EDG. Заметим, что ∆HDG и ∆EHG равны, ведь у них одинаковую длину имеют ребра DH, EH, ребро GH – общее, а ∠DHG и ∠EHG прямые. Тогда одинаковы отрезки EG и DG. Это означает, что ∆EGD – равнобедренный.
В ∆EGDMG– это медиана. Так как ∆EGD – равнобедренный, то MG одновременно ещё и высота, поэтому MD⊥MG.
Аналогично ∆EHD– равнобедренный (EH = HD), а потому MH в нем – и медиана, и высота. Поэтому MD⊥MH.
Получили, что MD перпендикулярен и MH, и MG, то есть двум прямым в плоскости MHG. Тогда MD перпендикулярен всей плоскости MHG, и, в частности, отрезку HK: HK⊥MD.
Но также MD⊥MG. Получается, KH перпендикулярен двум прямым в плоскости EDG, и потому он является перпендикуляром к плоскости EDG. Значит, именно его длину нам и надо найти.
Рассмотрим ∆MDH. Он прямоугольный, а ∠MDH = 45° (угол между стороной и диагональю квадрата). Тогда длину MH можно найти так:
Так как ребро GH перпендикулярно грани АЕНD, то ∆MHG – прямоугольный. Тогда по теореме Пифагора можно найти MG:
Далее можно найти HK разными способами, но проще воспользоваться подобием ∆MHG и ∆MKH. Они оба – прямоугольные, и у них есть общий угол ∠KMH, этого достаточно для подобия треугольников. Записываем пропорцию:
Здесь слева записано отношение сторон, лежащих против ∠KMH, а справа – отношение сторон, лежащих против прямых углов (то есть отношение гипотенуз). Используем пропорцию дальше:
Задание. Найдите расстояние между прямыми ВС и DH:
Решение. ВС и DH – скрещивающиеся. Надо найти общий перпендикуляр к ним. В данном случае он очевиден – это отрезок CD. Действительно, CD⊥ВС как стороны квадрата АВСD, но и DH⊥CD как стороны в другом квадрате, СDHG.. Длина же ребра CD равна единице, ведь у куба все ребра одинаковы.
Ответ: 1.
Задание. Каково расстояние между прямыми ВС и DG:
Решение.На грани СDHG опустим из С перпендикуляр СК на диагональ GD:
Будет ли СК являться расстоянием между ВС и DG? Ясно, что СК⊥DG. При этом ребро ВС перпендикулярно грани СGHD, так как ВС⊥СG и ВС⊥СD. Значит, также ВС⊥СК. То есть СК – общий перпендикуляр к ВС и DG, и по определению как раз и является искомым расстоянием.
Длину СК найдем из прямоугольного ∆СKG. ∠СGK составляет 45°, ведь это угол между диагональю DG и стороной квадрата СG. Тогда можно записать:
Задание. Найдите расстояние между ребрами АВ и HG:
Решение. Здесь ребра АВ и HG параллельны, так как каждая их них параллельна ребру CD. Проведем отрезок АН. Так как и АВ, и HG перпендикулярны грани АЕНD, то эти ребра одновременно перпендикулярны и АН. То есть АН – общий перпендикуляр к АВ и HG, и поэтому именно его длину и надо найти.
Сделать это можно из прямоугольного ∆АНD, в котором ∠НАD составляет 45°:
Задание. Чему равно расстояние между ребром AB и диагональю FD:
Решение. Пусть А1, D1, H1 и Е1 – середины ребер АВ, DC, HG, и EF соответственно. Проведем через А1, D1, H1 плоскость. Диагональ FD пересечет ее в какой-нибудь точке К:
Сначала покажем, что плоскости α и ADH (то есть нижняя грань) параллельны.
Заметим, что в четырехугольнике АА1D1D стороны АА1 и DD1 параллельны (ведь они лежат на сторонах квадрата АВСD) и одинаковы (ведь они составляют половину от длины ребер АВ и CD, то есть имеют длину 0,5). Тогда АА1D1D – параллелограмм. Более того, раз у него есть прямые углы ∠А1АDи ∠АDD1, то можно утверждать, что АА1D1D – прямоугольник. Тогда АD||A1D1. Аналогично можно показать, что DHH1D1 – прямоугольник, и DH||D1H1.
Далее можно действовать разными способами. Первый способ – это использование признака параллельности плоскостей (теорема 9 из этого урока). Так как в α есть пересекающиеся прямые А1D1и D1H1, а в плоскости ADH находятся прямые AD и DH, и АD||A1D1, и DH||D1H1, то по этому признаку α||ADH.
Однако, если этот признак вдруг оказался «забыт», то можно использовать отрезок DD1. Он перпендикулярен и грани ADHE, и плоскости α, ведь в каждой из них есть по две прямых, перпендикулярных ему. Это AD и DH на грани ADHE и A1D1и D1H1 в α. Тогда α и ADH перпендикулярны одной и той же прямой, а потому они параллельны. Так или иначе, мы выяснили, что α||ADH.
Отсюда вытекает, что α должна проходить через середину Е1. Действительно, расстояние между параллельными плоскостями не зависит от выбора точек измерения. В данном случае оно равно отрезку АА1, то есть 0,5. Но FE– это также общий перпендикуляр к α и ADH. Значит, α пересекает FE в точке, находящейся на расстоянии 0,5 от Е. А это как раз и есть середина FE, то есть точка Е1.
Далее докажем, что точка К, в которой прямая FD пересекает α – это середина отрезка Е1D1. Для этого удобно отдельно показать плоскость, проходящую через параллельные ребра FE и CD, то есть четырехугольник FEDC:
Заметим, так как ребра FE и CD перпендикулярны верхней и нижней грани, то они перпендикулярны и отрезкам FC и ED, то есть FEDC прямоугольник. Тогда FC||ED, и ∠Е1FD = ∠D1DF (накрест лежащие углы при секущей FD). ∠FKE1 и ∠DKD1 одинаковы уже как вертикальные углы. Тогда ∆FKE1 и ∆DKD1 подобны по 2 углам. Но отрезки FE1 и DD1 одинаковы как половины равных ребер FE и CD. Получается, что ∆FKE1 и ∆DKD1 равны, и поэтому Е1К = KD1. Это и значит, что К – середина Е1D1.
Также отметим, что Е1D1 – диагональ в четырехугольнике А1Е1Н1D1. Докажем, что А1Е1Н1D – это квадрат. Ранее мы уже показали, что АА1D1D и DHH1D1 – прямоугольники. Аналогично можно продемонстрировать, что прямоугольниками являются также АА1Е1Е и ЕЕ1Н1Н. Из этого вытекает равенство сторон:
То есть в А1Е1Н1D1 все стороны одинаковы, и эта фигура – ромб. Теперь надо показать, что и углы в этом четырехугольнике составляют 90°. Продемонстрируем это на примере ∠А1D1H1. AD⊥CDHG и AD||A1D1, поэтому А1D1⊥CDHG. Значит, также А1D перпендикулярна любой прямой на грани CDHG, в том числе и D1H1. То есть ∠А1D1H1 = 90°. Но если в ромбе хотя бы один угол прямой, то он является квадратом.
Итак, мы выяснили, что А1Е1Н1D1 – квадрат, а К – середина его диагонали Е1D1. Получается, что К – точка пересечения диагоналей квадрата А1Е1Н1D1, ведь эта точка пересечения как раз делит диагонали пополам.
Теперь мы можем наконец доказать, что А1К – это и есть искомое расстояние. Действительно, так как АВ – перпендикуляр к α, та А1К принадлежит α, то А1К⊥АВ. Но как же доказать, что А1К⊥FD. Здесь поможет теорема о трех перпендикулярах. Е1К – это проекция FK на α, и Е1К⊥А1К, ведь диагонали квадрата пересекаются под прямым углом. Раз отрезок А1К перпендикулярен проекции, то он перпендикулярен и самой наклонной, то есть А1К⊥FK.
Осталось лишь вычислить длину А1К. Для этого по аналогии с предыдущими задачами используем прямоугольный∆А1Е1К, в котором ∠А1Е1К = 45°:
Отвлечемся от куба и рассмотрим другую задачу.
Задание. В ∆АВС вписана окружность. Через центр этой окружности (точку О) проведена прямая ОН, причем она перпендикулярна плоскости АВС. Верно ли, что точка Н находится на одинаковом расстоянии от прямых АВ, АС и ВС?
Решение. Пусть N, K и M – точки касания окружности и сторон АВ, АС и ВС соответственно. Тогда ОN, OK и OM– радиусы, а они должны быть перпендикулярны касательным, то есть
Заметим, что ОN, OK и OM – это также проекции прямых HN, HK и HM соответственно. Раз отрезки АВ, АС и ВС перпендикулярны этим проекциям, то они должны быть перпендикулярны и наклонным:
Это значит, что HN, HK и HM– это расстояния от H до сторон ∆АВС. Осталось показать, что они одинаковы. Это можно сделать с помощью ∆HON, ∆HOK и ∆HOM. Они все прямоугольные, причем катет OH– общий, а катеты ON, OM и OK одинаковы как радиусы одной окружности. Отсюда вытекает вывод, что эти треугольники равны, то есть одинаковы и их гипотенузы HN, HKи HM, ч. т. д.
Теперь снова вернемся к кубу, чтобы на практике научиться определять угол между прямой и плоскостью.
Задание. Найдите угол между ребром куба BD и гранью СDHG:
Решение. ВС – это перпендикуляр к грани СDHG, поэтому CD– проекция BD на грань СDHG. Тогда нам надо найти ∠BDC. Он составляет 45°, так как это угол между стороной и диагональю квадрата АВСD:
Ответ: 45°.
Задание. Вычислите угол между ребром CD и плоскостью BDHF:
Решение. Нам надо из С опустить перпендикуляр на BDHF. Несложно догадаться, что для этого надо на грани ABCD опустить перпендикуляр СК на диагональ BD:
Действительно, СK⊥BD. Надо найти ещё одну прямую в BDHF, перпендикулярную СК. И такой прямой может быть BF. Так как BF перпендикулярна всей грани АВСD, то она обязательно перпендикулярна и СК. Получаем, что СК⊥BF и CK⊥BD, и тогда СK⊥BDHF.
Если СK– перпендикуляр, то KD – это проекция СD. Тогда искомый нами угол – это ∠СDK. Он равен 45°, ведь BD – диагональ квадрата АВСD, а CD – его сторона.
Ответ: 45°
Задание. Чему равен угол между прямой BD и плоскостью ABGH:
Решение. На нижней грани АЕНD опустим на АН перпендикуляр DK:
Заметим, что ребро АВ перпендикулярно грани АЕНD, поэтому KD⊥АВ. Но также KD⊥AH (мы специально построили так KD). Тогда можно утверждать, что KD – это перпендикуляр ко всей плоскости АВGH.
В таком случае BK – это проекция BD на AB. Значит, нам необходимо вычислить ∠DBK. Его можно найти из прямоугольного ∆DBK, но сперва надо вычислить длины сторон KD и BD.
ВD найдем из прямоугольного ∆ABD:
Теперь мы можем найти ∠DBK, а точнее его синус, из ∆DBK:
По таблице синусов легко определить, что ∠DBK = 30°.
Ответ: 30°.
В ходе сегодняшнего урока мы узнали о перпендикуляре к плоскости. Перпендикуляры используются для определения расстояний в стереометрии, а также угла между прямой и плоскостью.
Примечание. Текст задачи взят с форума.
Задача.
| Катеты прямоугольного треугольника АВС равны 9 и 12 см. Через середину гипотенузы (точку О) провели перпендикуляр к плоскости треугольника, равный 6см. Найти расстояние от концов перпендикуляра до катетов. | Катети прямокутного трикутника АВС дорівнюють 9 і 12 см Через середину гіпотенузи (точку О) провели перпендикуляр до площини трикутника, рівний 6см. Знайти відстань від кінців перпендикуляра до катетів. |
Решение.
Отобразим условие задачи на рисунке
Обратим внимание на то, что ON и OM являются перпендикулярами к катетам прямоугольного треугольника, поскольку нам необходимо найти расстояние KN и KM.
Рассмотрим отрезок NO. Он является перпендикуляром к CB. Угол ACB также вляется прямым по условию задачи. Таким образом, треугольники ABC и OBN – подобны по признаку равенства углов (см. подобие треугольников). Угол В – общий, а, поскольку CA и NO являются перпендикулярами к CB – то остальные углы также равны (один прямой, второй равен 180 градусов минус сумма остальных углов, равенство которых мы уже доказали).
Коэффициент подобия треугольников равен соотношению BO к BA. Поскольку точка О – точка касания медианы прямоугольного треугольника к гипотенузе, то есть AO = OB, то коэффициент подобия будет равен 1:2.
Откуда ON = CA / 2 = 9 / 2 = 4,5
Расстояние же KN найдем по теореме Пифагора.
KN = √(4,5 2 + 6 2 ) = 7,5 см
Аналогично, найдем расстояние до второго катета:
Перпендикулярность в пространстве с примерами решения
Содержание:
Перпендикулярность в пространстве
В этом параграфе вы ознакомитесь с понятиями угла между прямыми в пространстве, угла между прямой и плоскостью, угла между двумя плоскостями; узнаете, что такое ортогональная проекция, изучите свойство ортогональной проекции многоугольника.
Угол между прямыми в пространстве
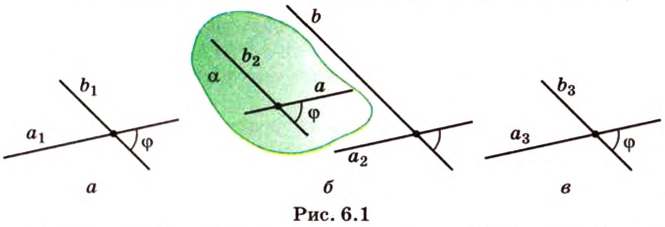
Поскольку две любые пересекающиеся прямые пространства лежат в одной плоскости, то угол между ними определим так же, как в планиметрии. Определение. Углом между двумя пересекающимися прямыми называют величину того из углов, образовавшихся при их пересечении, который не превышает (рис. 33.1).
Угол между двумя параллельными прямыми считают равным Следовательно, если — угол между двумя прямыми, лежащими в одной плоскости, то .
Введем понятие угла между скрещивающимися прямыми. Определение. Углом между двумя скрещивающимися прямыми называют угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.
Пусть прямые скрещивающиеся. Через точку М пространства проведем прямые так, что (рис. 33.2). По определению угол между скрещивающимися прямыми равен углу между пересекающимися прямыми .
Возникает естественный вопрос: зависит ли угол между данными скрещивающимися прямыми от выбора точки М ? Ответить на этот вопрос помогает следующая теорема.
Теорема 33.1. Угол между двумя пересекающимися прямыми равен углу между двумя другими пересекающимися прямыми, соответственно параллельными данным.
Воспользовавшись теоремой 33.1, можно показать, что угол между скрещивающимися прямыми равен углу между пересекающимися прямыми , где
Например, на рисунке 33.3 изображена треугольная призма . Угол между скрещивающимися прямыми и ВС равен углу между пересекающимися прямыми и ВС.
Определение. Две прямые в пространстве называют перпендикулярными, если угол между ними равен 90°.
Заметим, что перпендикулярные прямые могут как пересекаться, так и быть скрещивающимися.
Если прямые перпендикулярны, то записывают: Два отрезка в пространстве называют перпендикулярными, если они лежат на перпендикулярных прямых.
Например, ребра AD и куба перпендикулярны (рис. 33.4). Действительно, поскольку то угол между прямыми AD и равен углу между прямыми AD и . Но , поэтому .
Пример:
На рисунке 33.5 изображен куб . Найдите угол между прямыми и .
Решение:
Соединим точки . Поскольку , то точки лежат в одной плоскости. Эта плоскость пересекает параллельные плоскости по параллельным прямым . Следовательно, угол между прямыми равен углу . Соединим точки В и D. Отрезки равны как диагонали равных квадратов. Следовательно, треугольник равносторонний. Тогда . Ответ : 60°.
Перпендикулярность прямой и плоскости
В повседневной жизни мы говорим: флагшток перпендикулярен поверхности земли (рис. 34.1), мачты парусника перпендикулярны поверхности палубы (рис. 34.2), шуруп вкручивают в доску перпендикулярно ее поверхности (рис. 34.3) и т.п.
Эти примеры дают представление о прямой, перпендикулярной плоскости. Определение. Прямую называют перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости (рис. 34.4).
Если прямая перпендикулярна плоскости то записывают: Также принято говорить, что плоскость перпендикулярна прямой или прямая и плоскость перпендикулярны.
Из определения следует, что если прямая перпендикулярна плоскости то она пересекает эту плоскость.
Отрезок называют перпендикулярным плоскости, если он принадлежит прямой, перпендикулярной этой плоскости.
Например, интуитивно понятно, что ребро прямоугольного параллелепипеда перпендикулярно плоскости АВС (рис. 34.5). Доказать этот факт нетрудно, воспользовавшись следующей теоремой.
Теорема 34.1 (признак перпендикулярности прямой и плоскости). Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна самой плоскости.
На рисунке 34.5 прямая перпендикулярна двум пересекающимся прямым АВ и AD плоскости АВС. Следовательно, по признаку перпендикулярности прямой и плоскости а значит, и ребро также перпендикулярно плоскости АВС.
Теорему 34.1 часто используют на практике. Например, подставка для новогодней елки имеет форму крестовины. Если елку установить так, чтобы ее ствол был перпендикулярен направлениям крестовины, то елка будет стоять перпендикулярно плоскости пола (рис. 34.6).
Приведем теорему, которую можно рассматривать как еще один признак перпендикулярности прямой и плоскости.
Теорем а 34.2. Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости (рис. 34.7).
Например, на рисунке 34.5 прямая перпендикулярна плоскости АВС, а прямая параллельна прямой . Следовательно, по теореме 34.2 прямая также перпендикулярна плоскости АВС. Сформулируем теорему, являющуюся признаком параллельности двух прямых.
Теорем а 34.3. Если две прямые перпендикулярны одной и той же плоскости, то они параллельны (рис. 34.8). Справедлива и такая теорема.
Теорема 34.4. Через данную точку можно провести прямую, перпендикулярную данной плоскости, и притом только одну.
Пример:
Плоскость перпендикулярная катету АС прямоугольного треугольника АВС, пересекает катет АС в точке Е, а гипотенузу АВ — в точке F (рис. 34.9). Найдите отрезок EF, если АЕ : ЕС = 3 : 4, ВС = 21 см.
Решение:
Поскольку прямая АС перпендикулярна плоскости то прямая АС перпендикулярна любой прямой этой плоскости, в частности прямой EF. Прямые EF и ВС лежат в одной плоскости и перпендикулярны прямой АС, поэтому . Из этого следует, что треугольники AEF и подобны. Следовательно, можно записать: EF : СВ=АЕ : АС. Отсюда EF : 21 = 3 : 7, EF = 9 см. Ответ: 9 см.
Перпендикуляр и наклонная
Пусть фигура — параллельная проекция фигуры F на плоскость в направлении прямой Если , то фигуру называют ортогональной проекцией фигуры F на плоскость
Например, основание ABCD прямоугольного параллелепипеда является ортогональной проекцией основания на плоскость АВС в направлении прямой (рис. 35.1).
В дальнейшем, говоря о проекции фигуры, если не оговорено противное, будем иметь в виду ортогональную проекцию.
Пусть даны плоскость и не принадлежащая ей точка А . Через точку А проведем прямую перпендикулярную плоскости Пусть (рис. 35.2).
Отрезок АВ называют перпендикуляром, опущенным из точки А на плоскость точку В — основанием перпендикуляра. Основание В перпендикуляра АВ — это проекция точки А на плоскость .
Отметим на плоскости какую-нибудь точку С, отличную от точки В. Проведем отрезок АС (рис. 35.2). Отрезок АС называют наклонной, проведенной из точки А к плоскости точку С — основанием наклонной. Отрезок ВС является проекцией наклонной АС.
Теорема 35.1. Если из одной тонки проведены к плоскости перпендикуляр и наклонная, то наклонная больше перпендикуляра.
Пример:
Докажите, что если точка, не принадлежащая плоскости многоугольника, равноудалена от его вершин, то проекцией этой точки на плоскость многоугольника является центр его описанной окружности.
Решение:
Проведем доказательство для треугольника. Для других многоугольников доказательство будет аналогичным. Пусть точка М не принадлежит плоскости АВС, причем МА = = МВ = МС. Опустим из точки М перпендикуляр МО на плоскость АВС (рис. 35.3). Докажем, что точка О — центр описанной окружности треугольника АВС. Поскольку , то . В прямоугольных треугольниках МОА, МОВ, МОС катет МО — общий, гипотенузы равны, следовательно, эти треугольники равны по гипотенузе и катету. Из равенства данных треугольников следует, что ОА = ОВ = ОС, то есть точка О — центр описанной окружности треугольника АВС.
Заметим, что когда надо определить расстояние между двумя геометрическими фигурами, то стремятся найти расстояние между их ближайшими точками. Например, из курса планиметрии вы знаете, что расстоянием от точки, не принадлежащей прямой, до этой прямой называют расстояние от данной точки до ближайшей точки на прямой, то есть длину перпендикуляра, опущенного из точки на прямую. Теорема 35.1 показывает, что целесообразно принять следующее определение.
Определение. Если точка не принадлежит плоскости, то расстоянием от точки до плоскости называют длину перпендикуляра, опущенного из точки на плоскость. Если точка принадлежит плоскости, то считают, что расстояние от точки до плоскости равно нулю.
Пример:
Докажите, что если прямая параллельна плоскости, то все точки прямой равноудалены от плоскости.
Решение:
Пусть А и В — две произвольные точки прямой параллельной плоскости Точки — основания перпендикуляров, опущенных соответственно из точек А и В на плоскость (рис. 35.4). Докажем, что .
По теореме 34.3 . Следовательно, точки лежат в одной плоскости. Плоскость проходит через прямую параллельную плоскости и пересекает плоскость по прямой . Тогда по теореме 30.2 получаем: . Таким образом, в четырехугольнике каждые две противолежащие стороны параллельны. Следовательно, четырехугольник — параллелограмм. Отсюда Так как точки А и В выбраны на прямой произвольно, то утверждение задачи доказано.
Доказанное свойство позволяет принять следующее определение. Определение. Расстоянием от прямой до параллельной ей плоскости называют расстояние от любой точки этой прямой до плоскости. Используя результат, полученный в ключевой задаче 2, можно решить следующую задачу.
Пример:
Докажите, что если две плоскости параллельны, то все точки одной плоскости равноудалены от другой плоскости. Определение. Расстоянием между двумя параллельными плоскостями называют расстояние от любой точки одной плоскости до другой плоскости.
Результаты, полученные в ключевых задачах 2 и 3, часто используют в практической деятельности, например в строительстве (рис. 35.5).
Теорема 35.2 (теорема о трех перпендикулярах). Если прямая, принадлежащая плоскости, перпендикулярна проекции наклонной к этой плоскости, то она перпендикулярна и самой наклонной. И наоборот, если прямая, принадлежащая плоскости, перпендикулярна наклонной к этой плоскости, то она перпендикулярна и проекции наклонной на эту плоскость.
Доказательство. Докажем первую часть теоремы.Пусть прямая принадлежащая плоскости перпендикулярна проекции ВС наклонной АС (рис. 35.6). Докажем, что . Имеем: следовательно, . Получили, что прямая а перпендикулярна двум пересекающимся прямым АВ и ВС плоскости АВС; следовательно,. Поскольку то Доказательство второй части теоремы аналогично доказательству первой части.
Пример:
Точка М не принадлежит плоскости выпуклого многоугольника и равноудалена от всех прямых, содержащих его стороны. Проекцией точки М на плоскость многоугольника является точка О, принадлежащая многоугольнику. Докажите, что точка О — центр вписанной окружности многоугольника.
Решение:
Проведем доказательство для треугольника. Для других многоугольников доказательство будет аналогичным. Опустим из точки О перпендикуляры ON, ОК и ОЕ соответственно на прямые АВ, ВС и СА (рис. 35.7). Соединим точку М с точками Е, К и N.
Отрезок ON является проекцией наклонной MN на плоскость АВС. По построению . Тогда по теореме о трех перпендикулярах получаем:
Аналогично можно доказать, что . Следовательно, длины отрезков MN, МК и ME — расстояния от точки М до прямых АВ, ВС и СА соответственно. По условию MN = МК = МЕ.
В прямоугольных треугольниках MON, МОК, МОЕ катет МО общий, гипотенузы равны; следовательно, данные треугольники равны по катету и гипотенузе. Из равенства этих треугольников следует, что ON = ОК = ОЕ.
Длины отрезков ON, ОК и ОЕ являются расстояниями от точки О до прямых, содержащих стороны треугольника АВС. Мы показали, что эти расстояния равны. Так как точка О принадлежит треугольнику АВС, то точка О — центр вписанной окружности треугольника АВС.
Угол между прямой и плоскостью
Вы знаете, что в давние времена путешественники ориентировались по звездам. Они измеряли угол, который образовывал с плоскостью горизонта луч, идущий от данной точки к небесному телу.
Сегодня человеку в своей деятельности также важно определять углы, под которыми наклонены к данной плоскости некоторые объекты (рис. 36.1). Эти примеры показывают, что целесообразно ввести понятие угла между прямой и плоскостью.
Определение. Если прямая параллельна плоскости или принадлежит ей, то считают, что угол меж ду такой прямой и плоскостью равен 0°.
Если прямая перпендикулярна плоскости, то считают, что угол между такой прямой и плоскостью равен .
Если прямая пересекает плоскость и не перпендикулярна ей, то углом между такой прямой и плоскостью называют угол между прямой и ее проекцией на плоскость (рис. 36.2).
Из определения следует, что если — угол между прямой и плоскостью, то .
Также принято говорить, что прямая образует угол с плоскостью.
Углом между отрезком и плоскостью называют угол между прямой, содержащей этот отрезок, и плоскостью.
Например, рассмотрим куб (рис. 36.3). Угол между диагональю грани и плоскостью АВС равен 45°. Действительно, прямая АВ — проекция прямой на плоскость АВС. Тогда угол между прямой и плоскостью АВС равен величине угла . Поскольку четырехугольник — квадрат, то .
Пример:
Докажите, что если из одной точки к плоскости проведены наклонные, образующие равные углы с плоскостью, то проекция данной точки на плоскость равноудалена от оснований наклонных.
Решение:
Пусть МЛ и М В — наклонные, образующие с плоскостью равные углы, отрезки ОА и ОВ — проекции этих наклонных (рис. 36.4). Докажем, что ОА = ОВ.
Прямая ОА является проекцией прямой МА на плоскость Так как угол МАО острый, то он равен углу между прямыми ОА и МА. Следовательно, величина угла МАО равна углу между наклонной МА и плоскостью . Аналогично можно доказать, что величина угла МВО равна углу между наклонной МВ и плоскостью По условию .
Поскольку то . Получаем, что прямоугольные треугольники МОА и МОВ равны по катету и противолежащему острому углу. Отсюда .
Двугранный угол. Угол между плоскостями
На рисунке 37.1 изображена фигура, состоящая из двух полуплоскостей, имеющих общую границу. Эта фигура делит пространство на две части, выделенные на рисунке 37.2 разными цветами. Каждую из этих частей вместе с полуплоскостями называют двугранным углом. Полуплоскости называют гранями двугранного угла, а их общую границу — ребром двугранного угла. Как видим, «желтый» и «синий» двугранные углы, изображенные на рисунке 37.2, существенно различаются. Это различие выражается следующим свойством. На гранях двугранного угла выберем произвольные точки М и N (рис. 37.3).
Отрезок MN принадлежит «желтому» двугранному углу, а «синему» двугранному углу принадлежат лишь концы отрезка. В дальнейшем, говоря «двугранный угол», будем подразумевать такой двугранный угол, который содержит любой отрезок с концами на его гранях («желтый» двугранный угол).
Наглядное представление о двугранном угле дают полуоткрытая классная доска, двускатная крыша, открытый ноутбук (рис. 37.4).
Двугранный угол считают пространственным аналогом угла на плоскости. Вы знаете, как определяют величину угла на плоскости. Научимся определять величину двугранного угла.
Отметим на ребре MN двугранного угла произвольную точку О. Через точку О в гранях двугранного угла проведем лучи ОА и ОВ перпендикулярно ребру MN (рис. 37.5). Угол АОВ, образованный этими лучами, называют линейным углом двугранного угла. Поскольку и , то . Таким образом, если через произвольную точку ребра двугранного угла провести плоскость перпендикулярно ребру, то эта плоскость пересечет двугранный угол по его линейному углу.
Определение. Величиной двугранного угла называют величину его линейного угла.
Двугранный угол называют острым, прямым, тупым или развернутым, если его линейный угол соответственно острый, прямой, тупой или развернутый.
Например, рассмотрим куб (рис. 37.6). Двугранный угол с ребром , грани которого принадлежат плоскостям и является прямым. Действительно, поскольку и , то угол ADC — линейный угол двугранного угла с ребром .
Угол ADC прямой.
При пересечении двух плоскостей образуются четыре двугранных угла, отличных от развернутого (рис. 37.7). Здесь возможны два случая:
- все четыре двугранных угла прямые (рис. 37.7, а);
- из четырех двугранных углов два равных угла острые и два равных угла тупые (рис. 37.7, б).
В обоих случаях из четырех двугранных углов найдется такой, величина которого не превышает 90°.
Определение. Углом между двумя пересекающимися плоскостями называют величину того из образовавшихся двугранных углов, который не превышает 90°. Угол между двумя параллельными плоскостям и равен 0°.
Углом между многоугольником и плоскостью, которой много угольник не принадлежит, называют угол между плоскостью, содержащей многоугольник, и данной плоскостью.
Углом между двумя многоугольниками, лежащими в разных плоскостях, называют угол между плоскостями, в которых лежат эти многоугольники.
Пример:
Прямоугольные треугольники и АВМ имеют общий катет АВ (рис. 37.8). Отрезок МВ перпендикулярен плоскости АВС. Известно, что МВ = 4 см, АС = 6 см, МС = 10 см. Найдите угол между плоскостями АВС и АМС.
Решение:
Отрезок ВА является проекцией наклонной МА на плоскость АВС. Так как , то по теореме о трех перпендикулярах . Следователь но, угол МАВ — линейный угол двугранного угла с ребром АС, грани которого принадлежат плоскостям АВС и АМС. Поскольку угол МАВ острый, то угол между плоскостями АВС и АМС равен величине угла МАВ.
Для стороны AM прямоугольного треугольника АМС можно записать: . Отсюда . Для угла МАВ прямоугольного треугольника МАВ запишем: . Отсюда и . Ответ: 30°.
Имеет место теорема, устанавливающая связь между площадью данного многоугольника и площадью его проекции.
Теорема 37.1 (площадь ортогональной проекции многоугольника). Площадь проекции выпуклого многоугольника равна произведению его площади и косинуса угла а между многоугольником и его проекцией, где .
Определение. Две плоскости называют перпендикулярными, если угол между ними равен 90°.
Если плоскости перпендикулярны, то записывают: . Также принято говорить, что плоскость перпендикулярна плоскости или плоскость перпендикулярна плоскости .
Наглядное представление о перпендикулярных плоскостях дают плоскости стены и потолка комнаты, плоскости двери и пола, плоскости сетки и теннисного корта (рис. 37.9).
Очевидно, что перпендикулярные плоскости при пересечении образуют четыре прямых двугранных угла (рис. 37.10).
Теорема 37.2 (признак перпендикулярности плоскостей). Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Например, плоскость грани прямоугольного параллелепипеда , (рис. 37.11) перпендикулярна плоскости грани ABCD. Действительно, плоскость проходит через прямую , перпендикулярную плоскости АВС.
ГЛАВНОЕ В ПАРАГРАФЕ 5
Угол между прямыми в пространстве Углом между двумя пересекающимися прямыми называют величину того из углов, образовавшихся при их пересечении, который не превышает 90°. Считают, что угол между двумя параллельными прямыми равен 0°. Углом между двумя скрещивающимися прямыми называют угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым. Две прямые в пространстве называют перпендикулярными, если угол между ними равен 90°.
Перпендикулярность прямой и плоскости
- Прямую называют перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
- Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна самой плоскости.
- Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости.
- Если две прямые перпендикулярны одной и той же плоскости, то они параллельны.
- Через данную точку можно провести прямую, перпендикулярную данной плоскости, и притом только одну.
Ортогональная проекция фигуры
Пусть фигура — параллельная проекция фигуры F на плоскость в направлении прямой . Если , то фигуру называют ортогональной проекцией фигуры F на плоскость
Расстояние от точки до плоскости
Если точка не принадлежит плоскости, то расстоянием от точки до плоскости называют длину перпендикуляра, опущенного из точки на плоскость. Если точка принадлежит плоскости, то считают, что расстояние от точки до плоскости равно нулю.
Расстояние от прямой до параллельной ей плоскости
Расстоянием от прямой до параллельной ей плоскости называют расстояние от любой точки этой прямой до плоскости.
Расстояние между двумя параллельными плоскостями
Расстоянием между двумя параллельными плоскостями называют расстояние от любой точки одной плоскости до другой плоскости.
Теорема о трех перпендикулярах
Если прямая, принадлежащая плоскости, перпендикулярна проекции наклонной к этой плоскости, то она перпендикулярна и самой наклонной. И наоборот, если прямая, принадлежащая плоскости, перпендикулярна наклонной к этой плоскости, то она перпендикулярна и проекции наклонной на эту плоскость.
Угол между прямой и плоскостью
- Если прямая параллельна плоскости или принадлежит ей, то считают, что угол между такой прямой и плоскостью равен 0°.
- Если прямая перпендикулярна плоскости, то считают, что угол между такой прямой и плоскостью равен 90°.
- Если прямая пересекает плоскость и не перпендикулярна ей, то углом между такой прямой и плоскостью называют угол между прямой и ее проекцией на плоскость.
Величина двугранного угла
Величиной двугранного угла называют величину его линейного угла.
Угол между двумя пересекающимися плоскостями
Углом между двумя пересекающимися плоскостями называют величину того из образовавшихся двугранных углов, который не превышает 90°.
Площадь ортогональной проекции многоугольника
Площадь проекции выпуклого многоугольника равна произведению его площади и косинуса угла а между многоугольником и его проекцией, где
Перпендикулярные плоскости
Две плоскости называют перпендикулярными, если угол между ними равен 90°.
Признак перпендикулярности плоскостей
Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Векторы и координаты в пространстве
- Множества
- Рациональные уравнения
- Рациональные неравенства и их системы
- Предел числовой последовательности
- Предел и непрерывность числовой функции одной переменной
- Функции, их свойства и графики
- Параллельность в пространстве
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
[spoiler title=”источники:”]
http://profmeter.com.ua/communication/learning/course/course7/lesson433/
http://www.evkova.org/perpendikulyarnost-v-prostranstve
[/spoiler]
Геометрия, 10 класс
Урок №10. Перпендикуляр и наклонные
Перечень вопросов, рассматриваемых в теме.
- Определение перпендикуляра, наклонной и проекции наклонной на плоскость;
- Доказательство теоремы о трех перпендикулярах;
- Определение угла между прямой и плоскостью.
Глоссарий по теме
Теорема о трех перпендикулярах: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.
Обратная теорема: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.
Определение: углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость.
Основная литература:
Атанасян Л. С., Бутузов В. Ф. Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни. – 4-е изд. – М.: Просвещение, 2017. – 255 с.
Дополнительная литература:
Глазков Ю. А., Юдина И. И., Бутузов В. Ф. Рабочая тетрадь по геометрии для 10 класса. Базовый и профильный уровень. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения
Рассмотрим плоскость α и точку А, не лежащую в этой плоскости (рис. 1). Проведем через точку А прямую, перпендикулярную к плоскости α, и обозначим буквой Н точку пересечения этой прямой с плоскостью α. Отрезок АН называется перпендикуляром, проведенным из точки А к плоскости α, а точка Н — основанием перпендикуляра. Отметим в плоскости α какую-нибудь точку М, отличную от Н, и проведем отрезок AM. Он называется наклонной, проведенной из точки А к плоскости α, а точка М – основанием наклонной. Отрезок НМ называется проекцией наклонной на плоскость α.
(Рис. 1)
Рассмотрим прямоугольный треугольник АМН. Сторона АН — катет, а сторона AM — гипотенуза, поэтому АН < AM. Поэтому перпендикуляр, проведенный из данной точки к плоскости, меньше любой наклонной, проведенной из той же точки к этой плоскости.
Следовательно, из всех расстояний от точки А до различных точек плоскости α наименьшим является расстояние до точки Н. Это расстояние, т. е. длина перпендикуляра, проведенного из точки А к плоскости α, называется расстоянием от точки А до плоскости α.
Стоит отметить, что в случае двух параллельных плоскостей, расстоянием между ними будет расстояние от произвольной точки одной плоскости до другой плоскости. Например, все точки потолка находятся на одинаковом расстоянии от пола. Если же прямая параллельна плоскости, то все точки прямой равноудалены от этой плоскости. В этом случае расстояние от произвольной точки прямой до плоскости называется расстоянием между прямой и параллельной ей плоскостью. Например, все точки прямой b равноудалены от потолка комнаты.
Если мы имеем дело со скрещивающимися прямыми, то расстоянием между ними будет расстояние между одной из этих прямых и плоскостью, проходящей через другую прямую параллельно первой.
Сформулируем теорему о трех перпендикулярах: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.
(Рис. 2)
На рисунке 2: АН — перпендикуляр к плоскости α, AM — наклонная, а — прямая, проведенная в плоскости α через точку М перпендикулярно к проекции наклонной НМ. Докажем, что прямая а перпендикулярна наклонной AM.
Рассмотрим плоскость АМН. Прямая а перпендикулярна к НМ по условию. Так как прямая а, лежит в плоскости α, а эта плоскость перпендикулярна отрезку AH, то прямая а перпендикулярна к этой плоскости. Отсюда следует, что прямая а перпендикулярна к любой прямой, лежащей в плоскости АМН, в частности прямая а перпендикулярна отрезку АМ. Теорема доказана.
Эта теорема называется теоремой о трех перпендикулярах, так как в ней говорится о связи между тремя перпендикулярами АН, НМ и AM.
Справедлива также обратная теорема: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.
Введем теперь понятие проекции произвольной фигуры на плоскость. Проекцией точки на плоскость называется основание перпендикуляра, проведенного из этой точки к плоскости, если точка не лежит в плоскости, и сама точка, если она лежит в плоскости.
Обозначим буквой F какую-нибудь фигуру в пространстве. Если мы построим проекции всех точек этой фигуры на данную плоскость, то получим фигуру F1, которая называется проекцией фигуры F на данную плоскость (рис. 3).
(Рис. 3)
Докажем теперь, что проекцией прямой на плоскость, не перпендикулярную к этой прямой, является прямая (рис. 4).
Данную плоскость обозначим буквой α. Произвольную прямую, не перпендикулярную к плоскости, обозначим буквой а. Из какой-нибудь точки М прямой а проведем перпендикуляр МН к плоскости α и рассмотрим плоскость β, проходящую через прямую a и перпендикуляр МН. Плоскости α и β пересекаются по некоторой прямой а1.
Докажем, что эта прямая и является проекцией прямой а на плоскость α. В самом деле, возьмем произвольную точку М1 прямой а и проведем в плоскости β прямую М1Н1, параллельную прямой МН.
Так как отрезок MH перпендикуляр к плоскости α и отрезок MH параллелен М1Н1, то отрезок М1Н1 тоже перпендикулярен плоскости α.
Этим мы доказали, что проекция произвольной точки прямой а лежит на прямой а1.
Аналогично доказывается, что любая точка прямой а1 является проекцией некоторой точки прямой а. Следовательно, прямая а1 — проекция прямой а на плоскость α. Что и требовалось доказать.
(Рис. 4)
Теперь введем понятие угла между прямой и плоскостью.
Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость.
Примеры и разбор решения заданий тренировочного модуля
Пример 1. Докажем, что угол между φ0 между данной прямой AM и плоскостью α является наименьшим из всех углов φ, которые данная прямая образует с прямыми, проведенными в плоскости α через точку А.
(Рис. 5)
Обозначим буквой Н основание перпендикуляра (рис. 5), проведенного из точки М к плоскости α.
Рассмотрим произвольную прямую р в плоскости α, проходящую через точку А и отличную от прямой АН.
Угол между прямыми AM и р обозначим через φ.
Докажем, что φ больше чем φ0.
Из точки М проведем перпендикуляр MN к прямой р. Если точка N совпадает с точкой А, то φ равняется 90 градусам и поэтому φ больше чем φ 0. Рассмотрим случай, когда точки А и N не совпадают. Отрезок AM — общая гипотенуза прямоугольных
треугольников ANM и АНМ, поэтому
sinφ=MN/AM
Так как наклонная MN больше, чем перпендикуляр МН, то синус угла φ больше, чем синус угла φ0. Поэтому угол φ больше, чем угол φ0. Что и требовалось доказать.
Тестовый вопрос №7. Прямая AM перпендикулярна плоскости равностороннего треугольника ABC, точка H середина стороны BC. Найдите угол между прямой MH и плоскостью ABC, если AM = a, HB = a.
Решение. Искомый угол – MHA.
Рассмотрим треугольник ABC. Он равносторонний. Это означает, что его медиана так же является высотой и биссектрисой. Так как HB = a, следовательно, любая сторона треугольника имеет длину 2a. Рассмотрим треугольник AHB. Он прямоугольный, т.к. AH медиана и высота. По теореме Пифагора вычислим длину стороны AH: 
Далее рассмотрим треугольник MHA, он прямоугольный, т.к. MA перпендикулярна плоскости ABC. Зная это мы можем выразить тангенс искомого угла: 
Ответ: ∠MHA = 30˚.
Тестовый вопрос №8. Из точки O к плоскости α проведена наклонная, длина которой равна 17 см, проекция наклонной равна 15 см. На каком расстоянии от плоскости находится точка O?
Решение. Нарисуем рисунок. OH – перпендикуляр, OM – наклонная, длина которой 17 см, MH – проекция наклонной, длина которой 15 см.
Треугольник OHM – прямоугольный, т.к. OH – перпендикуляр. Поэтому OH – искомое расстояние. Найдем его по теореме Пифагора: 
Ответ: 8 сантиметров.
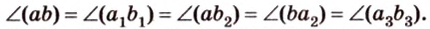
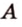 прямой
прямой 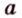
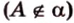 ;
;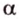
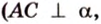
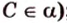 ;
;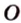 и
и 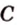 прямую
прямую 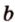 .
.