Как найти растояние от точки до плоскости

Поиск расстояния от точки до плоскости — частая задача, возникающая при решении различных задач аналитической геометрии, например, к этой задаче можно свести нахождение расстояния между двумя скрещивающимися прямыми или между прямой и параллельной ей плоскостью.

Рассмотрим плоскость $β$ и точку $M_0$ с координатами $(x_0;y_0; z_0)$, не принадлежащую плоскости $β$.

Ниже рассмотрено как найти расстояние от точки до плоскости координатным методом.

Вывод формулы для координатного метода поиска расстояния от точки до плоскости в пространстве

Перпендикуляр из точки $M_0$, пересекающийся с плоскостью $β$ в точке $M_1$ с координатами $(x_1;y_1; z_1)$, лежит на прямой, направляющим вектором которой является нормальный вектор плоскости $β$. При этом длина единичного вектора $n$ равна единице. Соответственно этому, расстояние от $β$ до точки $M_0$ составит:

$ρ= |vec{n} cdot vec{M_1M_0}|left(1right)$, где $vec{M_1M_0}$ — нормальный вектор плоскости $β$, а $vec{n}$ — единичный нормальный вектор рассматриваемой плоскости.

В случае, когда уравнение плоскости задано в общем виде $Ax+ By + Cz + D=0$, координаты нормального вектора плоскости представляют собой коэффициенты уравнения ${A;B;C}$, а единичный нормальный вектор в этом случае имеет координаты, вычисляемые по следующему уравнению:

$vec{n}= frac{{A;B;C}}{sqrt{A^2 + B^2 + C^2}}left(2right)$.

Теперь можно найти координаты нормального вектора $vec{M_1M_0}$:

$vec{M_0M_1}= {x_0 – x_1;y_0-y_1;z_0-z_1}left(3right)$.

Также выразим коэффициент $D$, используя координаты точки, лежащей в плоскости $β$:

$D= Ax_1+By_1+Cz_1$

Координаты единичного нормального вектора из равенства $(2)$ можно подставить в уравнение плоскости $β$, тогда мы имеем:

$ρ= frac{|A(x_0 -x_1) + B(y_0-y_1)+C(z_0-z_1)|}{sqrt{A^2+B^2+C^2}}= frac{|Ax_0+ By_0 + Cz_0-(Ax_1+By_1+Cz_1)|}{sqrt{A^2+B^2+C^2}} = frac{Ax_0+ By_0 + Cz_0 + D}{sqrt{A^2+B^2+C^2}}left(4right)$

Равенство $(4)$ является формулой для нахождения расстояния от точки до плоскости в пространстве.

Общий алгоритм для нахождения расстояния от точки $M_0$ до плоскости

1. Если уравнение плоскости задано не в общей форме, для начала необходимо привести его к общей.
2. После этого необходимо выразить из общего уравнения плоскости нормальный вектор данной плоскости через точку $M_0$ и точку, принадлежащую заданной плоскости, для этого нужно воспользоваться равенством $(3)$.
3. Следующий этап — поиск координат единичного нормального вектора плоскости по формуле $(2)$.
4. Наконец, можно приступить к поиску расстояния от точки до плоскости, это осуществляется с помощью вычисления скалярного произведения векторов $vec{n}$ и $vec{M_1M_0}$.

Расстояние от точки до плоскости

Расстояние от точки до плоскости – длина перпендикуляра, опущенного из точки на эту плоскость.

Способы нахождения расстояния от точки до плоскости

Существует, по крайней мере, два способа найти расстояние от точки до плоскости: геометрический и алгебраический.

При геометрическом способе нужно сначала понять, как расположен перпендикуляр из точки на плоскость: может он лежит в какой –то удобной плоскости, является высотой в какой-нибудь удобном (или не очень) треугольнике, а может этот перпендикуляр вообще является высотой в какой-нибудь пирамиде.

После этого первого и самого сложного этапа задача распадается на несколько конкретных планиметрических задач (быть может, в разных плоскостях).

При алгебраическом способе для того, чтобы найти расстояние от точки до плоскости, нужно ввести систему координат, найти координаты точки и уравнение плоскости, и после этого применить формулу расстояния от точки до плоскости.

Кажется с первого взгляда, что алгебраический способ легче, но это… далеко не всегда так. Проблемы обычно возникают как раз с нахождением координат точки и управления плоскости, особенно если система координат была введена не самым удобным способом. Для удобства приведём плюсы и минусы обоих способов в табличке:

Сейчас мы разберём один достаточно хитрый пример, двумя способами.

Задача: в кубе ( text{ABCD}~{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}) с ребром ( 2) точки ( displaystyle M) — середина ребра ( {{A}_{1}}{{D}_{1}}). Найти расстояние от точки ( displaystyle C) до плоскости ( displaystyle A{{B}_{1}}M).

Геометрический способ

Куда же опускается перпендикуляр из точки ( displaystyle C) на плоскость ( displaystyle A{{B}_{1}}M)?

Смотрим на ( displaystyle Delta A{{B}_{1}}M) – оказывается, он равнобедренный – ( displaystyle {{B}_{1}}M=AM)!

Проведём ( displaystyle CA) и ( displaystyle C{{B}_{1}}). Зачем? А они тоже равны ( displaystyle CA) и ( displaystyle C{{B}_{1}}).

Отметим точку ( displaystyle K) — середину ( displaystyle A{{B}_{1}}) — и проведём ( displaystyle MK) и ( displaystyle CK). Треугольники ( displaystyle A{{B}_{1}}M) и ( displaystyle A{{B}_{1}}C) — равнобедренные, поэтому ( displaystyle MKbot A{{B}_{1}}) и ( displaystyle CKbot A{{B}_{1}}).

И вот теперь! Стереометрическая теорема идёт в ход: признак перпендикулярности прямой и плоскости.

( displaystyle left{ begin{array}{l}A{{B}_{1}}bot MK\A{{B}_{1}}bot CKend{array} right.Rightarrow A{{B}_{1}}bot CMK).

Остался один шаг: проведём ( displaystyle CHbot MK) (в плоскости ( displaystyle CMK), естественно).

Что же можно сказать о ( displaystyle CH)?

( displaystyle CHbot MK) по построению

( displaystyle CHbot A{{B}_{1}}) – так как ( displaystyle A{{B}_{1}}bot CMK) и значит, ( displaystyle A{{B}_{1}}) перпендикулярна всякой прямой в плоскости ( displaystyle CMK), в частности и ( displaystyle CH).

Итак,

( displaystyle left{ begin{array}{l}CHbot MK\CHbot A{{B}_{1}}end{array} right.Rightarrow CHbot A{{B}_{1}}M) – Ура!

Искомый перпендикуляр из точки ( displaystyle C) на плоскость ( displaystyle A{{B}_{1}}M) — это высота в ( displaystyle Delta CMK). Осталось найти эту высоту.

( displaystyle C{{D}_{1}}=sqrt{{{2}^{2}}+{{2}^{2}}}=2sqrt{2}) (из ( displaystyle C{{C}_{1}}{{D}_{1}})); ( displaystyle M{{D}_{1}}=1) (по условию)

( displaystyle {{B}_{1}}M=sqrt{{{2}^{2}}+{{1}^{2}}}=sqrt{5};~{{B}_{1}}K=frac{A{{B}_{1}}}{2}=sqrt{2})

Расстояние от точки до плоскости

Чтобы найти расстояние между точкой и плоскостью, нужно построить между ними перпендикуляр, длина которого и будет ему равна. Существует несколько методов построения перпендикуляра между точкой и плоскостью.

ПОСТРОЕНИЕ ПЕРПЕНДИКУЛЯРА ИЗ ТОЧКИ НА ПЛОСКОСТЬ

Самый простой способ – просто провести искомый перпендикуляр. Сложность этого метода в том, что не всегда очевидно, куда именно упадет перпендикуляр. Если это перпендикуляр к плоскости, то по признаку перпендикулярности он должен быть перпендикулярен любой прямой на этой плоскости.

Значит этот перпендикуляр упадет так, что мы сможем доказать его перпендикулярность к плоскости. Точка пересечения перпендикуляра и плоскости будет единственной возможной.

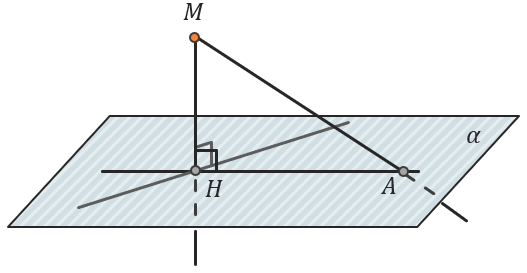
Из точки (M), не лежащей в плоскости α, проведем перпендикуляр (text{MH}):

Этот метод стоит применять тогда, когда мы знаем, чему равны две стороны получившегося прямоугольного треугольника (text{MHA}), чтобы иметь возможность найти длину перпендикуляра (text{MH} )как третью сторону треугольника.

ПОСТРОЕНИЕ ПЕРПЕНДИКУЛЯРА ИЗ ТОЧКИ НА ПРЯМОЙ К ПЛОСКОСТИ

Если с построением перпендикуляра из точки возникают трудности, можно использовать этот способ.

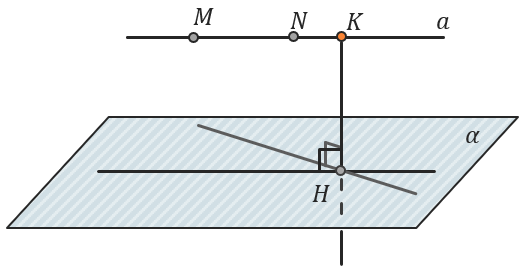
Вместо того, чтобы сразу проводить перпендикуляр из точки M, можно провести через неё прямую (a), так, что (a parallel alpha). Таким образом каждая точка на этой прямой будет находиться на равном расстоянии от плоскости, что и точка М. Так мы сможем выбрать более удобную точку, проведя перпендикуляр из которой будет легко доказать, что это действительно перпендикуляр к плоскости.

Снова перпендикулярность прямой к плоскости будет доказываться через признак перпендикулярности.

Например, в данном случае прямая, проведенная через точку K будет падать в точку H – точку пересечения прямых на плоскости, так, что KH перпендикулярна каждой из этих прямых:

ПОСТРОЕНИЕ ПЕРПЕНДИКУЛЯРА ИЗ ТОЧКИ ПЛОСКОСТИ К ПЛОСКОСТИ

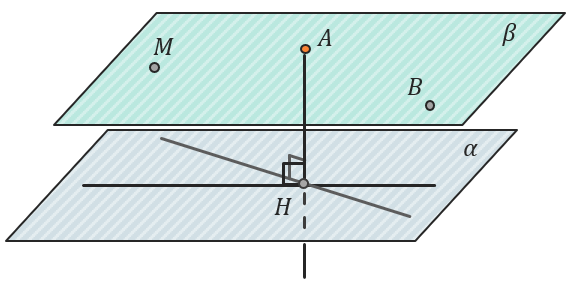
Аналогично можно построить через точку (M) плоскость β так, что (beta parallel alpha). Тогда любая другая точка на этой плоскости буде находится от плоскости (alpha) на том же расстоянии, что и точка (M). Так можно выбрать любую другую удобную точку, например точку (А), и найти расстояние от неё до плоскости (alpha).

НАХОЖДЕНИЕ ДЛИНЫ ПЕРПЕНДИКУЛЯРА ЧЕРЕЗ ОБЪЕМ

Если в задаче возникают трудности с построением перпендикуляра каким-либо способом выше, то можно решить задачу алгебраически. Самый простой способ найти длину перпендикуляра – представить его как высоту геометрического тела. Тогда, зная его объем, можно будет выразить высоту, а значит найти расстояние от точки до плоскости.

Например:

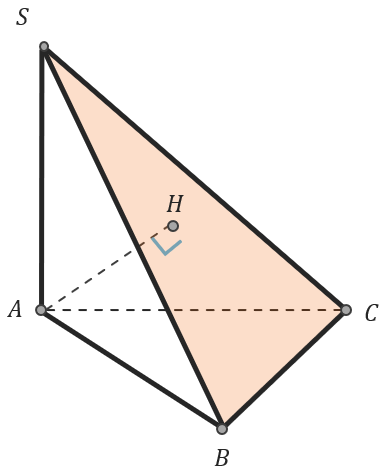
Дана пирамида (text{SABC}). Отрезок (text{SA}) перпендикулярен плоскости (text{ABC}). Выразите длину от точки (A) до плоскости (text{SBC}).

В данной задаче мы не можем построить перпендикуляр ни от точки, ни от прямой, ни от плоскости, т. к. не знаем, куда этот перпендикуляр упадет. Решим задачу через объем пирамиды.

1. Если (text{AS}) перпендикулярна плоскости (text{ABC}), то можем использовать этот отрезок как высоту пирамиды и представить её объем так:

(V_{text{SABC}} = frac{1}{3}S_{text{ABC}} bullet SA)

1. С другой стороны, можем представить (text{AH })как высоту пирамиды (text{ASBC}) с вершиной (A):

(V_{text{ASBC}} = frac{1}{3}S_{text{SBC}} bullet AH)

1. Таким образом можем приравнять два объема, т. к. по сути мы выразили два одинаковых объема по-разному:

(V_{text{SABC}} = V_{text{ASBC}})

(frac{1}{3}S_{text{ABC}} bullet SA = frac{1}{3}S_{text{SBC}} bullet AH)

(AH = frac{S_{text{ABC}} bullet SA}{S_{text{SBC}}})

В статье мы расскажем о нескольких способах того, как найти расстояние от точки до плоскости, а для лучшего понимания рассмотрим пример на эту тему.

Определение расстояние от точки до плоскости

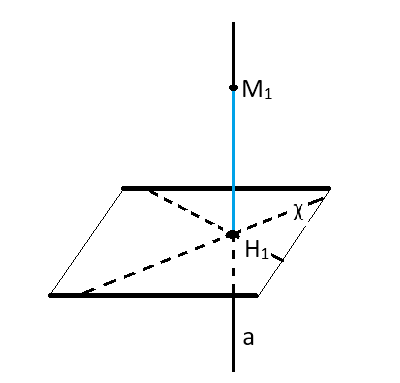
Пусть дана плоскость χ, а в пространстве задана точка M₁. Через неё проходит прямая, перпендикулярная нашей χ. H₁ обозначим общую точку их пересечения. Отрезок M₁H₁ является перпендикуляром из M₁ к [χ]. В обсуждаемом случае H₁ есть основание перпендикуляра. 

Докажем это:

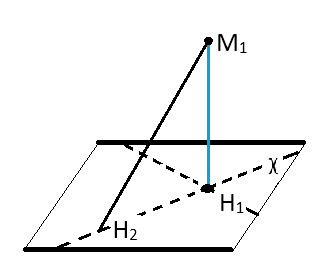
Если H₂ на χ не совпадает с H₁, то мы имеем прямоугольный треугольник M₂H₁H₂. При этом M₂H₁ есть его катет, а M₂H₂ гипотенуза. Длина гипотенузы треугольника всегда больше, чем длина катета. Доказательство завершено.

Способы найти расстояние от точки до плоскости

Мы имеем точку M₁ в трёхмерном пространстве с декартовыми координатами x₁, y₁, z₁ и плоскость [χ]. Покажем, как в этом случае найти расстояние от M₁ до [χ].

• Первый способ.

  Он основан на использовании координат точки H₁, которая является основанием перпендикуляра, проведённого из M₁ к [χ]. После этого вычисление искомой величины происходит достаточно просто.

• Второй способ.

  Сначала составляем уравнение прямой, которая перпендикулярна χ и проходит через M₁. Затем выясняем координаты (x₂, y₂, z₂) пересечения прямой [a] и [χ]. Вычисляем расстояние от точки M₁ до плоскости χ, формула, по которой это делается, следующая:

[mathrm{M}_{1} mathrm{H}_{1}=sqrt{left(mathrm{x}_{2}-mathrm{x}_{1}right)^{2}+left(mathrm{y}_{2}-mathrm{y}_{1}right)^{2}+left(mathrm{z}_{2}-mathrm{z}_{1}right)^{2}}]

• Третий способ.

  В прямоугольной декартовой системе координат у нас имеется плоскость χ. Её нормальное уравнение можно записать в виде:

  cosα * x + cosβ * y + cosγ * z – p = 0

  M₁H₁ вычисляется с помощью формулы:

  M₁H₁ = cosα * x + cosβ * y + cosγ * z – p

Это следует из теоремы, гласящей, что если в трёхмерном пространстве имеется точка M₁(x₁,y_1,z₁) и имеется нормальное уравнение плоскости, которое можно записать в виде cosα * x + cosβ * y + cosγ * z – p = 0, то расстояние от точки до плоскости будет равно

M₁H₁ = cosα * x + cosβ * y + cosγ * z – p

потому что x=x₁, y=y₁, z=z₁.