Данная статья рассказывает об определении расстояния от точки до плоскости. произведем разбор методом координат, который позволит находить расстояние от заданной точки трехмерного пространства. Для закрепления рассмотрим примеры нескольких задач.
Расстояние от точки до плоскости – определение
Расстояние от точки до плоскости находится посредством известного расстояния от точки до точки, где одна из них заданная, а другая – проекция на заданную плоскость.
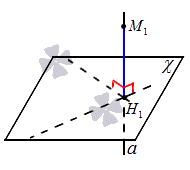
Когда в пространстве задается точка М1 с плоскостью χ, то через точку можно провести перпендикулярную плоскости прямую. Н1 является общей точкой их пересечения. Отсюда получаем, что отрезок М1Н1 – это перпендикуляр, который провели из точки М1 к плоскости χ, где точка Н1 – основание перпендикуляра.
Расстоянием от точки до плоскости называют расстояние от заданной точки к основанию перпендикуляра, который провели из заданной точки к заданной плоскости.
Определение может быть записано разными формулировками.
Расстоянием от точки до плоскости называют длину перпендикуляра, который провели из заданной точки к заданной плоскости.
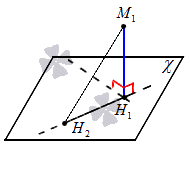
Расстояние от точки М1 к плоскости χ определяется так: расстояние от точки М1 до плоскости χ будет являться наименьшим от заданной точки до любой точки плоскости. Если точка Н2 располагается в плоскости χ и не равна точке Н2, тогда получаем прямоугольный треугольник вида М2H1H2 , который является прямоугольным, где имеется катет М2H1, М2H2 – гипотенуза. Значит, отсюда следует, что M1H1<M1H2. Тогда отрезок М2H1 считается наклонной, которая проводится из точки М1 до плоскости χ. Мы имеем, что перпендикуляр, проведенный из заданной точки к плоскости, меньше наклонной, которую проводят из точки к заданной плоскости. Рассмотрим этот случай на рисунке, приведенном ниже.
Расстояние от точки до плоскости – теория, примеры, решения
Существует ряд геометрических задач, решения которых должны содержать расстояние от точки до плоскости. Способы выявления этого могут быть разными. Для разрешения применяют теорему Пифагора или подобия треугольников. Когда по условию необходимо рассчитать расстояние от точки до плоскости, заданные в прямоугольной системе координат трехмерного пространства, решают методом координат. Данный пункт рассматривает этот метод.
По условию задачи имеем, что задана точка трехмерного пространства с координатами M1(x1, y1, z1) с плоскостью χ, необходимо определить расстояние от М1 к плоскости χ. Для решения применяется несколько способов решения.
Первый способ
Данный способ основывается на нахождении расстояния от точки до плоскости при помощи координат точки Н1, которые являются основанием перпендикуляра из точки М1 к плоскости χ. Далее необходимо вычислить расстояние между М1 и Н1.
Для решения задачи вторым способом применяют нормальное уравнение заданной плоскости.
Второй способ
По условию имеем, что Н1 является основанием перпендикуляра, который опустили из точки М1 на плоскость χ. Тогда определяем координаты (x2, y2, z2) точки Н1. Искомое расстояние от М1 к плоскости χ находится по формуле M1H1=(x2-x1)2+(y2-y1)2+(z2-z1)2, где M1(x1, y1, z1) и H1(x2, y2, z2). Для решения необходимо узнать координаты точки Н1.
Имеем, что Н1 является точкой пересечения плоскости χ с прямой a, которая проходит через точку М1, расположенную перпендикулярно плоскости χ. Отсюда следует, что необходимо составление уравнения прямой, проходящей через заданную точку перпендикулярно к заданной плоскости. Именно тогда сможем определить координаты точки Н1. Необходимо произвести вычисление координат точки пересечения прямой и плоскости.
Алгоритм нахождения расстояния от точки с координатами M1(x1, y1, z1) к плоскости χ:
- составить уравнение прямой а, проходящей через точку М1 и одновременно
- перпендикулярной к плоскости χ;
- найти и вычислить координаты (x2, y2, z2) точки Н1, являющимися точками
- пересечения прямой a с плоскостью χ;
- вычислить расстояние от М1 до χ, используя формулу M1H1=(x2-x1)2+(y2-y1)2+z2-z12.
Третий способ
В заданной прямоугольной системе координат Охуz имеется плоскость χ, тогда получаем нормальное уравнение плоскости вида cos α· x+cos β·y+cos γ·z-p=0. Отсюда получаем, что расстояние M1H1 с точкой M1(x1, y1, z1) , проведенной на плоскость χ, вычисляемое по формуле M1H1=cos α· x+cos β·y+cos γ·z-p. Эта формула справедлива, так как это установлено благодаря теореме.
Если задана точка M1(x1, y1, z1) в трехмерном пространстве, имеющая нормальное уравнение плоскости χ вида cos α· x+cos β·y+cos γ·z-p=0, тогда вычисление расстояния от точки до плоскости M1H1 производится из формулы M1H1=cos α· x+cos β·y+cos γ·z-p, так как x=x1, y=y1, z=z1.
Доказательство теоремы сводится к нахождению расстояния от точки до прямой. Отсюда получаем, что расстояние от M1 до плоскости χ – это и есть модуль разности числовой проекции радиус-вектора M1 с расстоянием от начала координат к плоскости χ. Тогда получаем выражение M1H1=npn→OM→-p. Нормальный вектор плоскости χ имеет вид n→=cos α, cos β, cos γ, а его длина равняется единице, npn→OM→ – числовая проекция вектора OM→=(x1, y1, z1) по направлению, определяемым вектором n→.
Применим формулу вычисления скалярных векторов. Тогда получаем выражение для нахождения вектора вида n→, OM→=n→·npn→OM→=1·npn→OM→=npn→OM→, так как n→=cos α, cos β, cos γ·z и OM→=(x1, y1, z1). Координатная форма записи примет вид n→, OM→=cos α· x1+cos β·y1+cos γ·z1, тогда M1H1=npn→OM→-p=cos α· x1+cos β·y1+cos γ·z1-p. Теорема доказана.
Отсюда получаем, что расстояние от точки M1(x1, y1, z1) к плоскости χ вычисляется при помощи подстановки в левую часть нормального уравнения плоскости cos α· x+cos β·y+cos γ·z-p=0 вместо х, у, z координаты x1, y1 и z1 ,относящиеся к точке М1, взяв абсолютную величину полученного значения.
Рассмотрим примеры нахождения расстояния от точки с координатами до заданной плоскости.
Вычислить расстояние от точки с координатами M1(5, -3, 10) к плоскости 2x-y+5z-3=0.
Решение
Решим задачу двумя способами.
Первый способ начнется с вычисления направляющего вектора прямой a. По условию имеем, что заданное уравнение 2x-y+5z-3=0 является уравнением плоскости общего вида, а n→=(2, -1, 5) является нормальным вектором заданной плоскости. Его применяют в качестве направляющего вектора прямой a, которая перпендикулярна относительно заданной плоскости. Следует записать каноническое уравнение прямой в пространстве, проходящее через M1(5, -3, 10) с направляющим вектором с координатами 2, -1, 5.
Уравнение получит вид x-52=y-(-3)-1=z-105⇔x-52=y+3-1=z-105.
Следует определить точки пересечения. Для этого нежно объединить уравнения в систему для перехода от канонического к уравнениям двух пересекающихся прямых. Данную точку примем за Н1. Получим, что
x-52=y+3-1=z-105⇔-1·(x-5)=2·(y+3)5·(x-5)=2·(z-10)5·(y+3)=-1·(z-10)⇔⇔x+2y+1=05x-2z-5=05y+z+5=0⇔x+2y+1=05x-2z-5=0
После чего необходимо разрешить систему
x+2y+1=05x-2z-5=02x-y+5z-3=0⇔x+2y=15x-2z=52x-y+5z=3
Обратимся к правилу решения системы по Гауссу:
120-150-252-153~120-10-10-2100-555~120-10-10-2100060⇒⇒z=06=0, y=-110·10+2·z=-1, x=-1-2·y=1
Получаем, что H1(1, -1, 0).
Производим вычисления расстояния от заданной точки до плоскости. Берем точки M1(5, -3, 10) и H1(1, -1, 0) и получаем
M1H1=(1-5)2+(-1-(-3))2+(0-10)2=230
Второй способ решения заключается в том, чтобы для начала привести заданное уравнение 2x-y+5z-3=0 к нормальному виду. Определяем нормирующий множитель и получаем 122+(-1)2+52=130. Отсюда выводим уравнение плоскости 230·x-130·y+530·z-330=0. Вычисление левой части уравнения производится посредствам подстановки x=5, y=-3, z=10, причем нужно взять расстояние от M1(5, -3, 10) до 2x-y+5z-3=0 по модулю. Получаем выражение:
M1H1=230·5-130·-3+530·10-330=6030=230
Ответ: 230.
Когда плоскость χ задается одним из способов раздела способы задания плоскости, тогда нужно для начала получить уравнение плоскости χ и вычислять искомое расстояние при помощи любого метода.
В трехмерном пространстве задаются точки с координатами M1(5, -3, 10), A(0, 2, 1), B(2, 6, 1), C(4, 0, -1). Вычислить расстяние от М1 к плоскости АВС.
Решение
Для начала необходимо записать уравнение плоскости, проходящее через заданные три точки с координатами M1(5, -3, 10), A(0, 2, 1), B(2, 6, 1), C(4, 0, -1).
Получим:
x-0y-2z-12-06-21-14-00-2-1-1=0⇔xy-2z-12404-2-2=0⇔⇔-8x+4y-20z+12=0⇔2x-y+5z-3=0
Отсюда следует, что задача имеет аналогичное предыдущему решение. Значит, расстояние от точки М1 к плоскости АВС имеет значение 230.
Ответ: 230.
Нахождение расстояния от заданной точки на плоскости или к плоскости, которым они параллельны, удобнее, применив формулу M1H1=cos α·x1+cos β·y1+cos γ·z1-p. Отсюда получим, что нормальные уравнения плоскостей получают в несколько действий.
Найти расстояние от заданной точки с координатами M1(-3, 2, -7) к координатной плоскости Охуz и плоскости, заданной уравнением 2y-5=0.
Решение
Координатная плоскость Оуz соответствует уравнению вида х=0. Для плоскости Оуz оно является нормальным. Поэтому необходимо подставить в левую часть выражения значения х=-3 и взять модуль значения расстояния от точки с координатами M1(-3, 2, -7) к плоскости. Получаем значение, равное -3=3.
После преобразования нормальное уравнение плоскости 2y-5=0 получит вид y-52=0. Тогда можно найти искомое расстояние от точки с координатами M1(-3, 2, -7) к плоскости2y-5=0. Подставив и вычислив, получаем 2-52=52-2.
Ответ: Искомое расстояние от M1(-3, 2, -7) до Оуz имеет значение 3, а до 2y-5=0 имеет значение 52-2.
Определение расстояния от точки до прямой
Расстояние от точки до прямой – это длина перпендикуляра, опущенного из точки на прямую. В начертательной геометрии она определяется графическим путем по приведенному ниже алгоритму.
Алгоритм
- Прямую переводят в положение, в котором она будет параллельна какой-либо плоскости проекции. Для этого применяют методы преобразования ортогональных проекций.
- Из точки проводят перпендикуляр к прямой. В основе данного построения лежит теорема о проецировании прямого угла.
- Длина перпендикуляра определяется путем преобразования его проекций или с использованием способа прямоугольного треугольника.
Пример
На следующем рисунке представлен комплексный чертеж точки M и прямой b, заданной отрезком CD. Требуется найти расстояние между ними.
Решение
Согласно нашему алгоритму, первое, что необходимо сделать, это перевести прямую в положение, параллельное плоскости проекции. При этом важно понимать, что после проведенных преобразований фактическое расстояние между точкой и прямой не должно измениться. Именно поэтому здесь удобно использовать метод замены плоскостей, который не предполагает перемещение фигур в пространстве.
Результаты первого этапа построений показаны ниже. На рисунке видно, как параллельно b введена дополнительная фронтальная плоскость П4. В новой системе (П1, П4) точки C”1, D”1, M”1 находятся на том же удалении от оси X1, что и C”, D”, M” от оси X.
Выполняя вторую часть алгоритма, из M”1 опускаем перпендикуляр M”1N”1 на прямую b”1, поскольку прямой угол MND между b и MN проецируется на плоскость П4 в натуральную величину. По линии связи определяем положение точки N’ и проводим проекцию M’N’ отрезка MN.
На заключительном этапе нужно определить величину отрезка MN по его проекциям M’N’ и M”1N”1. Для этого строим прямоугольный треугольник M”1N”1N0, у которого катет N”1N0 равен разности (YM1 – YN1) удаления точек M’ и N’ от оси X1. Длина гипотенузы M”1N0 треугольника M”1N”1N0 соответствует искомому расстоянию от M до b.
Второй способ решения
- Параллельно CD вводим новую фронтальную плоскость П4. Она пересекает П1 по оси X1, причем X1∥C’D’. В соответствии с методом замены плоскостей определяем проекции точек C”1, D”1 и M”1, как это изображено на рисунке.
- Перпендикулярно C”1D”1 строим дополнительную горизонтальную плоскость П5, на которую прямая b проецируется в точку C’2 = b’2.
- Величина расстояния между точкой M и прямой b определяется длиной отрезка M’2C’2, обозначенного красным цветом.
Похожие задачи:
- Определение расстояния от точки до плоскости
- Определение натуральной величины отрезка
- Расстояние между параллельными прямыми
Определение расстояния между: 1 – точкой и плоскостью; 2 – прямой и плоскостью; 3 – плоскостями; 4 – скрещивающимися прямыми рассматривается совместно, так как алгоритм решения для всех этих задач по существу одинаков и состоит из геометрических построений, которые нужно выполнить для определения расстояния между заданными точкой А и плоскостью α. Если и есть какое-то различие, то оно состоит лишь в том, что в случаях 2 и 3 прежде чем приступить к решению задачи, следует на прямой m (случай 2) или плоскости β (случай 3) отметить произвольную точку А. При определении расстояния между скрещивающимися прямыми предварительно заключаем их в параллельные плоскости α и β с последующим определением расстояния между этими плоскостями.
Рассмотрим каждый из отмеченных случаев решения задач.
1. Определение расстояния между точкой и плоскостью.
Расстояние от точки до плоскости определяется длиной отрезка перпендикуляра, опущенного из точки на плоскость.
Поэтому решение этой задачи состоит из последовательного выполнения следующих графических операций:
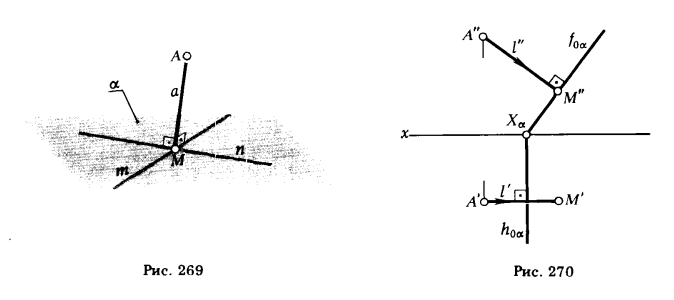
1) из точки А опускаем перпендикуляра на плоскость α (рис. 269);
2) находим точку М пересечения этого перпендикуляра с плоскостью М = а ∩ α;
3) определяем длину отрезка [AM].
Если плоскость α общего положения, то для того чтобы опустить на эту плоскость перпендикуляр, необходимо предварительно определить направление проекций горизонтали и фронтали этой плоскости. Нахождение точки встречи этого перпендикуляра с плоскостью также требует выполнения дополнительных геометрических построений.
Решение задачи упрощается, если плоскость α занимает частное положение относительно плоскостей проекций. В этом случае и проведение проекций перпендикуляра, и нахождение точки его встречи с плоскостью осуществляется без каких-либо дополнительных вспомогательных построений.
ПРИМЕР 1. Определить расстояние от точки А до фронтально проецирующей плоскости α (рис. 270).
РЕШЕНИЕ. Через А’ проводим горизонтальную проекцию перпендикуляра l’ ⊥ h0α, а через А” – его фронтальную проекцию l” ⊥ f0α. Отмечаем точку M” = l” ∩ f0α. Так как AM || π2, то [А” М”] == |АМ| = d.
Из рассмотренного примера видно, насколько просто решается задача, когда плоскость занимает проецирующее положение. Поэтому, если в исходных данных будет задана плоскость общего положения, то, прежде чем приступить к решению, следует перевести плоскость в положение, перпендикулярное к какой-либо плоскости проекции.
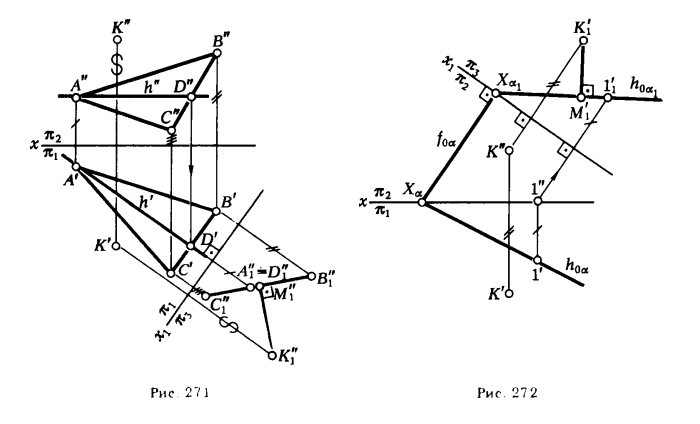
ПРИМЕР 2. Определить расстояние от точки К до плоскости, заданной ΔАВС (рис. 271).
РЕШЕНИЕ.
1. Переводим плоскость ΔАВС в проецирующее положение *. Для этого переходим от системы xπ2/π1 к x1π3/π1: направление новой оси х1 выбирается перпендикулярным к горизонтальной проекции горизонтали плоскости треугольника.
2. Проецируем ΔАВС на новую плоскость π3 (плоскость ΔАВС спроецируется на π3, в [ С”1В”1] ).
3. Проецируем на ту же плоскость точку К (К’ → К”1).
4. Через точку К”1 проводим (К”1М”1 )⊥ отрезку [С”1В”1]. Искомое расстояние d = |K”1M”1| .
Решение задачи упрощается, если плоскость задана следами, так как отпадает необходимость в проведении проекций линий уровня.
ПРИМЕР 3. Определить расстояние от точки К до плоскости α, заданной следами (рис. 272) .
* Наиболее рациональным путем перевода плоскости треугольника в проецирующее положение является способ замены плоскостей проекций, так как в этом случае достаточно построить только одну вспомогательную проекцию.
РЕШЕНИЕ. Заменяем плоскость π1 плоскостью π3, для этого проводим новую ось x1 ⊥ f0α. На h0α отмечаем произвольную точку 1′ и определяем ее новую горизонтальную проекцию на плоскости π3 (1′1). Через точки Xα1 (Хα1 = h0α1 ∩ x1 ) и 1′1 проводим h0α1. Определяем новую горизонтальную проекцию точки К → К’1. Из точки К’1 опускаем перпендикуляр на h0α1 и отмечаем точку его пересечения с h0α1 – М’1. Длина отрезка K’1M’1 укажет искомое расстояние.
2. Определение расстояния между прямой и плоскостью.
Расстояние между прямой и плоскостью определяется длиной отрезка перпендикуляра, опущенного из произвольной точки прямой на плоскость (см. рис. 248).
Поэтому решение задачи по определению расстояния между прямой m и плоскостью α ничем не отличается от рассмотренных в п. 1 примеров на определение расстояния между точкой и плоскостью (см. рис. 270 … 272). В качестве точки можно брать любую точку, принадлежащую прямой m.
3.Определение расстояния между плоскостями.
Расстояние между плоскостями определяется величиной отрезка перпендикуляра, опущенного из точки, взятой на одной плоскости, на другую плоскость.
Из этого определения вытекает, что алгоритм решения задачи по нахождению расстояния между плоскостями α и β отличается от аналогичного алгоритма решения задачи по определению расстояния между прямой m и плоскостью α лишь тем, что прямая m должна принадлежать плоскости α, т. е., чтобы определить расстояние между плоскостями α и β, следует:
1) взять в плоскости α прямую m;
2) выделить на прямой m произвольную точку А;
3) из точки А опустить перпендикуляр l на плоскость β;
4) определить точку М – точку встречи перпендикуляра l с плоскостью β;
5) определить величину отрезка [AM] .
На практике целесообразно пользоваться другим алгоритмом решения, который будет отличаться от приведенного лишь тем, что, прежде чем приступить к выполнению первого пункта, следует перевести плоскости в проецирующее положение.
Включение в алгоритм этой дополнительной операции упрощает выполнение всех без исключения остальных пунктов, что, в конечном счете, приводит к более простому решению.
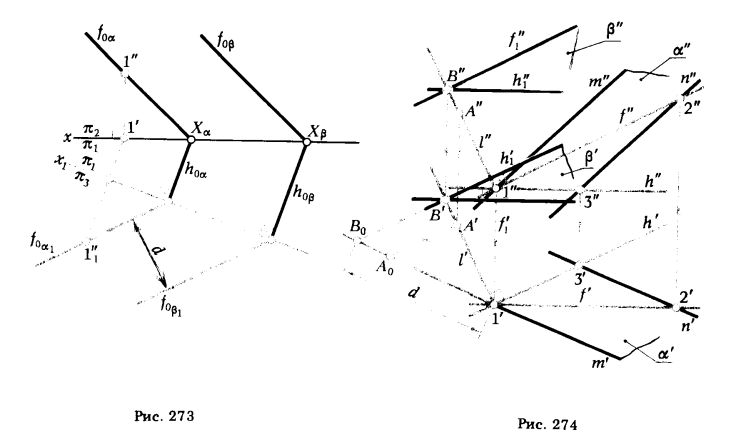
ПРИМЕР 1. Определить расстояние между плоскостями α и β (рис. 273).
РЕШЕНИЕ. Переходим от системы xπ2/π1 к x1π1/π3. По отношению к новой плоскости π3 плоскости α и β занимают проецирующее положение, поэтому расстояние между новыми фронтальными ,следами f0α1 и f0β1 является искомым.
В инженерной практике часто приходится решать задачу на построение плоскости, параллельной данной и удаленной от нее на заданное расстояние. Приведенный ниже пример 2 иллюстрирует решение такой задачи.
ПРИМЕР 2. Требуется построить проекции плоскости β, параллельной данной плоскости α (m || n), если известно, что расстояние между ними равно d (рис. 274).
РЕШЕНИЕ.
1. В плоскости α проводим произвольные горизонталь h (1, 3) и фронталь f (1,2).
2. Из точки 1 восставляем перпендикуляр l к плоскости α(l’ ⊥ h’, l” ⊥ f”).
3. На перпендикуляре l отмечаем произвольную точку А.
4. Определяем длину отрезка [1А] – [1’А0] (положение [1’А0] указывает на эпюре метрически неискаженное направление прямой l).
5. Откладываем на прямой (1’А0) от точки 1′ отрезок [1’В0] = d.
6. Отмечаем на проекциях l’ и l” точки В’ и В”, соответствующие точке В0.
7. Через точку В проводим плоскость β (h1 ∩ f1). Чтобы β || α, необходимо coблюдать условие h1 || h и f1 || f.
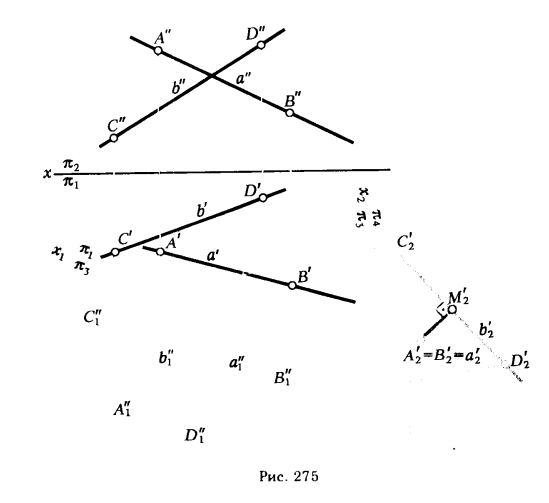
4. Определение расстояния между скрещивающимися прямыми.
Расстояние между скрещивающимися прямыми определяется длиной перпендикуляра, заключенного между параллельными плоскостями, которым принадлежат скрещивающиеся прямые.
Для того чтобы через скрещивающиеся прямые m и f провести взаимно параллельные плоскости α и β, достаточно через точку А (А ∈ m) провести прямую р, параллельную прямой f, а через точку В (В ∈ f) – прямую k, параллельную прямой m. Пересекающиеся прямые m и р, f и k определяют взаимно параллельные плоскости α и β (см. рис. 248, е). Расстояние между плоскостями α и β равно искомому расстоянию между скрещивающимися прямыми m и f.
Можно предложить и другой путь для определения расстояния между скрещивающимися прямыми, который состоит в том, что с помощью какого-либо способа преобразования ортогональных проекций одна из скрещивающихся прямых переводится в проецирующее положение. В этом случае одна проекция прямой вырождается в точку. Расстояние между новыми проекциями скрещивающихся прямых (точкой A’2 и отрезком C’2D’2) является искомым.
На рис. 275 приведено решение задачи на определение расстояния между скрещивающимися прямыми а и b, заданными отрезками [АВ] и [ CD]. Решение выполняют в следующей последовательности:
1. Переводят одну из скрещивающихся прямых (а) в положение, параллельное плоскости π3; для этого переходят от системы плоскостей проекции xπ2/π1 к новой x1π1/π3 , ось x1 проводят параллельно горизонтальной проекции прямой а . Определяют а”1 [А”1В”1] и b”1 [C”1D”1].
2. Путем замены плоскости π1 плоскостью π4 переводят прямую
а в положение а’2, перпендикулярное плоскости π4 (новую ось х2 проводят перпендикулярно а”1).
3. Строят новую горизонтальную проекцию прямой b’2 – [ C’2D’2].
4. Расстояние от точки А’2 до прямой C’2D’2 ( отрезок ( А’2М’2] (является искомым.
Следует иметь в виду, что перевод одной из скрещивающихся прямых в проецирующее положение является ничем иным, как переводом плоскостей параллелизма, в которые можно заключить прямые а и b, также в проецирующее положение.
В самом деле, переведя прямую а в положение, перпендикулярное плоскости π4, мы обеспечиваем перпендикулярность любой плоскости, содержащей прямую а, плоскости π4, в том числе и плоскости α, определяемой прямыми а и m (а ∩ m, m || b). Если мы теперь проведем прямую n, параллельную а и пересекающую прямую b, то мы получим плоскость β, являющуюся второй плоскостью параллелизма, в которую заключены скрещивающиеся прямые а и b. Так как β || α, то и β ⊥ π4.
§10. Построение перпендикуляра к плоскости. Расстояние от точки до плоскости.
В курсе Начертательной геометрии часто встречаются задачи, связанные с проведением перпендикуляра к заданной плоскости. Существует теорема о проекциях прямого угла, которая имеет следующую формулировку:
Если одна из сторон прямого угла параллельна какой-либо плоскости проекций, то проекция угла на эту плоскость является также прямым углом.
Исходя из этой теоремы, можно утверждать следующее:
Горизонтальная проекция перпендикуляра к плоскости перпендикулярна горизонтальной проекции горизонтали этой плоскости.
Фронтальная проекция перпендикуляра к плоскости перпендикулярна фронтальной проекции фронтали этой плоскости.
Задача 10.1.
Определить расстояние от точки D до плоскости, заданной треугольником АВС (рисунок 47).
Решение:
Расстояние от точки до плоскости измеряется по перпендикуляру, проведенному от этой точки до заданной плоскости. Поэтому для решения этой задачи нужно выполнить следующие действия, которые являются алгоритмом для решения задач на определение расстояний от точки до плоскости:
1. Проводим две проекции перпендикуляра к плоскости.
2. Находим точку пересечения этого перпендикуляра с данной плоскостью (первая позиционная задача).
3. Определяем натуральную величину отрезка от заданной точки до точки пересечения перпендикуляра с плоскостью.
Итак, проводим перпендикуляр от точки D до плоскости треугольника АВС. Построим в плоскости треугольника горизонталь h. На горизонтальной проекции эпюра восстановим перпендикуляр из точки D1 к прямой h1 (рис. 48). Мы получили горизонтальную проекцию перпендикуляра.
Проведем в плоскости треугольника фронталь и построим фронтальную проекцию перпендикуляра к плоскости. (Рис. 49).
Следующий шаг решения задачи – определение точки пересечения перпендикуляра с заданной плоскостью, то есть, предстоит решить первую позиционную задачу, алгоритм которой был рассмотрен в занятии 7 (§7). Заключаем перпендикуляр в проецирующую плоскость (ФПП), находим прямую пересечения ФПП с плоскостью треугольника АВС, а затем определяем точку К – искомую точку пересечения перпендикуляра с плоскостью (рис. 50).
Находим натуральную величину отрезка DK методом прямоугольного треугольника (см. Занятие 3), решение задачи представлено на рисунке 51.
Задача 10.2.
Построить эпюр прямой призмы, основанием которой является четырехугольник АВСD, высота призмы 30 мм. Исходные данные представлены на рисунке 52.
Решение.
Боковые ребра прямой призмы перпендикулярны ее основанию. Для решения задачи восстановим перпендикуляр к плоскости четырехугольника из любой вершины основания, например, из точки А.
На горизонтальной проекции нужно провести перпендикуляр к проекции горизонтали плоскости основания – это будет горизонтальная проекция перпендикуляра. Поскольку сторона АВ является горизонталью, проводим прямой угол к прямой А1В1 из точки А1 (рис. 53).
Прежде чем построить фронтальную проекцию, нужно провести в плоскости основания призмы фронталь и провести перпендикуляр к прямой А212 из точки А2 (рисунок 53).
Определяем натуральную величину высоты призмы. На построенном перпендикуляре возьмем произвольную точку Р и определим натуральную величину отрезка АР. Луч А1Р0 является направлением натуральной величины прямой АР (рисунок 54).
На луче А1Р0 отмеряем отрезок 30 мм и методом пропорций переносим полученную точку на перпендикуляр. Получаем точку Е – проекции Е1 и Е2 (рис. 55). Точка Е – это одна из вершин второго основания призмы.
Известно, что стороны оснований прямой призмы попарно параллельны, поэтому от точки Е достраиваем четырехугольник – второе основание призмы, соединяем вершины оснований ребрами, определяем видимость ребер и получаем окончательное решение задачи. Для наглядности грани призмы затонированы (рис.56).
Определение расстояний
Расстояния от точки до точки и от точки до прямой
Расстояние от точки до точки определяется длиной отрезка прямой, соединяющей эти точки. Как было показано выше, эту задачу можно решить либо методом прямоугольного треугольника, либо способом замены плоскостей проекций, переводя отрезок в положение линии уровня.
Расстояние от точки до прямой измеряется отрезком перпендикуляра, проведенного из точки к прямой. Отрезок этого перпендикуляра изображается в натуральную величину на плоскости проекций в том случае, если он проведен к проецирующей прямой. Таким образом, сначала прямую необходимо перевести в проецирующее положение, а затем из заданной точки опустить на нее перпендикуляр. На рис. 1 показано решение этой задачи. Для перевода прямой общего положения АВ в положение прямой уровня проводят x14IIА1В1. Затем АВ переводят в проецирующее положение введением дополнительной плоскости проекций П5, для чего проводят новую ось проекций х45А4В4.
Рисунок 1
Аналогично точкам А и В, на плоскость проекций П5 проецируют точку М.
Проекция К5 основания К перпендикуляра, опущенного из точки М на прямую АВ, на плоскости проекций П5 совпадет с соответствующими проекциями точек
А и В. Проекция М5К5 перпендикуляра МК есть натуральная величина расстояния от точки М до прямой АВ.
В системе плоскостей проекций П4/П5 перпендикуляр МК будет линией уровня, поскольку лежит в плоскости, параллельной плоскости проекций П5. Поэтому его проекция М4К4 на плоскость П4 параллельна x45, т.е. перпендикулярна проекции А4В4. Эти условия определяют положение проекции К4 основания перпендикуляра К, которое находят, проводя из М4прямую параллельно х45 до пересечения с проекцией А4В4. Остальные проекции перпендикуляра находят путем проецирования точки К на плоскости проекций П1 и П2.
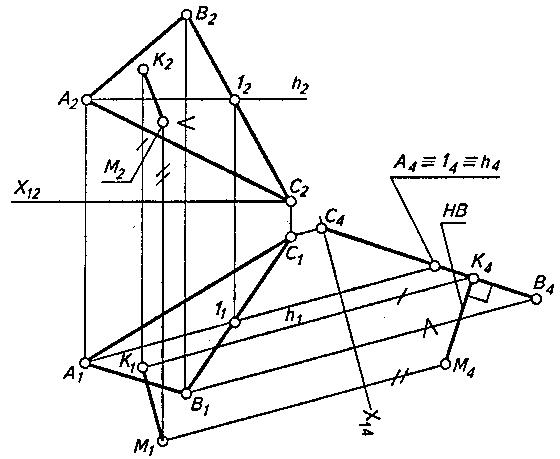
Расстояние от точки до плоскости
Решение этой задачи показано на рис. 2. Расстояние от точки М до плоскости (АВС) измеряется отрезком перпендикуляра, опущенного из точки на плоскость.
Рисунок 2
Так как перпендикуляр к проецирующей плоскости есть линия уровня, то переведем в это положение заданную плоскость, в результате чего на новой введенной плоскости проекций П4 получим вырожденную проекцию С4В4 плоскости ABC. Далее на П4 проецируем точку М. Натуральная величина расстояния от точки М до плоскости определяется отрезком перпендикуляра
[МК]=[М4К4]. Остальные проекции перпендикуляра строятся так же, как и в предыдущей задаче, т.е. с учетом того, что отрезок МК в системе плоскостей проекций П1/П4 является линией уровня и его проекция М1К1 параллельна оси
х14.
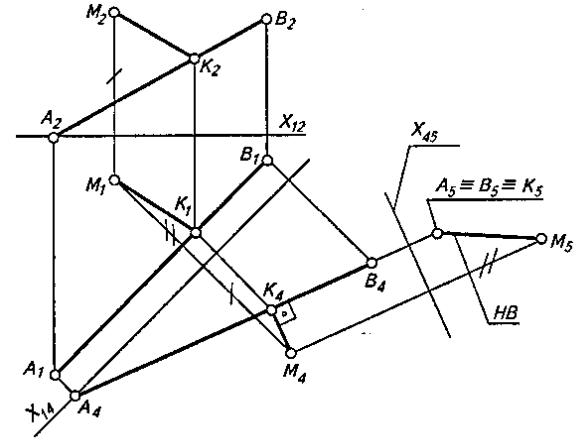
Расстояние между двумя прямыми
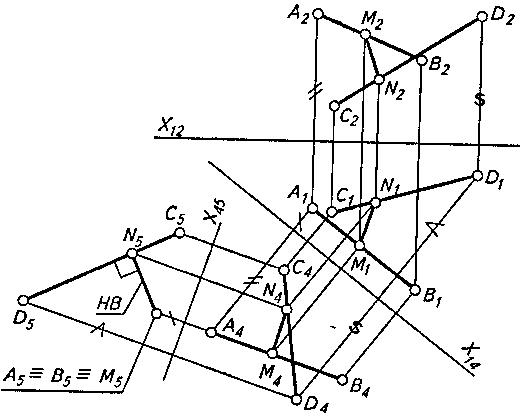
Кратчайшее расстояние между скрещивающимися прямыми измеряется величиной отрезка общего перпендикуляра к ним, отсекаемого этими прямыми. Задача решается выбором (в результате двух последовательных замен) плоскости проекций, перпендикулярной одной из скрещивающихся прямых. В этом случае искомый отрезок перпендикуляра будет параллелен выбранной плоскости проекций и изобразится на ней без искажения. На рис. 3 показаны две скрещивающиеся прямые, заданные отрезками АВ и CD.
Рисунок 3
Прямые в начале спроецированы на плоскость проекций П4, параллельную одной (любой) из них, например АВ, и перпендикулярную П1.
На плоскости проекций П4 отрезок АВ изобразится без искажения. Затем отрезки проецируют на новую плоскость П5 перпендикулярную той же прямой АВ и плоскости П4. На плоскости проекций П5 проекция перпендикулярного ей отрезка АВ вырождается в точку A5 =B5, а искомая величина N5M5 отрезка NM перпендикулярна C5D5 и изображается в натуральную величину. При помощи соответствующих линий связи строят проекции отрезка MN на первоначальном
чертеже. Как было показано ранее, проекция N4M4 искомого отрезка на плоскость П4 параллельна оси проекций x45, так как он в системе плоскостей проекций П4/П5 является линией уровня.
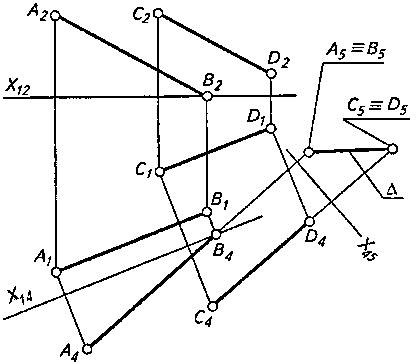
Задача по определению расстояния D между двумя параллельными прямыми АВ к CD – частный случай предыдущей (рис. 4).
Рисунок 4
Двойной заменой плоскостей проекций параллельные прямые переводят в проецирующее положение, в результате чего на плоскости проекций П5 будем иметь две вырожденные проекции А5 = В5 и С5 = D5 прямых АВ и CD. Расстояние между ними D будет равно его натуральной величине.
Расстояние от прямой до параллельной ей плоскости измеряется отрезком перпендикуляра, опущенного из любой точки прямой на плоскость. Поэтому достаточно плоскость общего положения преобразовать в положение проецирующей плоскости, взять напрямой точку, и решение задачи будет сведено к определению расстояния от точки до плоскости.
Чтобы определить расстояние между параллельными плоскостями, надо перевести их в проецирующее положение и построить перпендикуляр к вырожденным проекциям плоскостей, отрезок которого между ними и будет искомой величиной расстояния.
Соседние файлы в папке начертательная геометрия лекции
- #
15.01.2017126.25 Кб19Комплексный чертеж кривой линии.pdf
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #