Как найти раствор угла - Сайт, где вы сможете решить свои вопросы

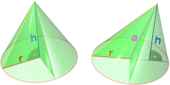
Угол раствора и радиус конуса способствуют вычислению всех возможных параметров конуса за счет двух треугольников, которые они образуют. Первый треугольник – равнобедренный, с двумя образующими и диаметром конуса, из которого можно рассчитать угол наклона конуса, между образующей и основанием. Второй треугольник – прямоугольный с высотой и радиусом в качестве катетов и образующей конуса, как гипотенузой. (рис. 40.2, 40.1)
β=(180°-α)/2
h=r tan⁡β
l=r/cos⁡β

Зная радиус конуса, можно сразу найти его диаметр, а также периметр основания и площадь, не прибегая к дополнительным заменам.
d=2r
P=2πr
S_(осн.)=πr^2

Чтобы найти площадь боковой поверхности, кроме радиуса понадобится образующая конуса, которая равна отношению радиуса к косинусу угла наклона, а чтобы найти площадь полной поверхности, к полученному выражению нужно прибавить площадь основания конуса.
S_(б.п.)=πrl=(πr^2)/cos⁡β
S_(п.п.)=S_(б.п.)+S_(осн.)=πr(r+l)=πr^2 (1+1/cos⁡β )

Объем конуса равен одной трети произведения площади основания на высоту, а так как высота представляет собой произведение радиуса на тангенс угла наклона, то объем получится уменьшенным в три раза произведением числа π на куб радиуса и тангенс угла.
V=(hS_(осн.))/3=(πr^3 tan⁡β)/3

Радиус сферы вписанной в конус зависит только от радиус и угла наклона, а радиус сферы описанной вокруг конуса можно найти через угол раствора конуса и радиус основания. (рис.40.3, 40.4)
r_1=r tan⁡〖β/2〗
R=r/sin⁡α

Источник

Калькулятор и формула для вычисления уклона конуса детали.

Уклон конуса может быть определен как отношение разности наибольшего диаметра конуса и наименьшего диаметра конуса к двойной длине конуса, тогда формула для определения уклона конуса детали будет иметь нижеследующий вид:

Также уклон конуса детали можно вычислить как половину конусности детали, такая формула будет следующей:

Либо уклон конуса можно рассчитать как тангенс угла наклона конуса по нижеследующей формуле:

Для определения уклона конуса необходимо ввести значения наибольшего диаметра конуса, наименьшего диаметра конуса, длины конуса и нажать кнопку «ВЫЧИСЛИТЬ.»

Результатом вычисления будет значение уклона конуса.

При проведении инженерных и других расчетах, а также работе с инженерной графикой и создании чертежей приходится создавать уклон. Конусность получила весьма широкое распространение, она применяется при изготовлении самых различных деталей. Показатель конусности рассчитывается в большинстве случаев при создании деталей, которые получили широкое распространение в сфере машиностроения. Рассмотрим основные параметры, особенности начертания и многие другие моменты подробнее.

Значение конусности

Рассматривая конусность следует учитывать, что этот показатель напрямую связан с уклоном. Этот параметр определяет отклонение прямой лини от вертикального ил горизонтального положения. При этом конусность 1:3 или конусность 1:16 существенно отличается. Определение уклона характеризуется следующими особенностями:

Под уклоном подразумевается отношение противолежащего катета прямоугольного треугольника к прилежащему. Этот параметр еще называют тангенс угла.
Для расчета примеряется следующая формула: i=AC/AB=tga.

Стоит учитывать, что нормальные конусности несколько отличаются от рассматриваемого ранее параметра. Это связано с тем, что конусностью называется соотношение диаметра основания к высоте.

Рассчитать этот показатель можно самым различным образом, наибольшее распространение получила формула K=D/h. В некоторых случаях обозначение проводится в процентах, так как этот переменный показатель применяется для определения всех других параметров.

Рассматривая конусность 1:7 и другой показатель следует также учитывать особенности отображения информации на чертеже. Чаще всего подобное отображение проводится при создании технической документации в машиностроительной области.

Связанные определения для конуса

Образующая конуса. Отрезок, соединяющий вершину и границу основания, называется образующей конуса.

Образующая поверхность конуса. Объединение образующих конуса называется образующей (или боковой) поверхностью конуса.

Коническая поверхность. Образующая поверхность конуса является конической поверхностью.

Высота конуса (H). Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка), называется высотой конуса.

Угол раствора конуса. Угол раствора конуса — угол между двумя противоположными образующими (угол при вершине конуса, внутри конуса).

Прямой конус. Если основание конуса имеет центр симметрии (например, является кругом или эллипсом) и ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром, то конус называется прямым. При этом прямая, соединяющая вершину и центр основания, называется осью конуса.

Косой (наклонный) конус. Косой (наклонный) конус — конус, у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии.

Круговой конус. Круговой конус — конус, основание которого является кругом.

Прямой круговой конус. Прямой круговой конус (часто его называют просто конусом) можно получить вращением прямоугольного треугольника вокруг прямой, содержащей катет (эта прямая представляет собой ось конуса).

Эллиптическим конус. Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом (последние два имеют бесконечный объём).

Усечённый конус. Часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием, называется усечённым конусом, или коническим слоем.

Обозначение конусности на чертеже

При создании технической документации должны учитываться все установленные стандарты, так как в противном случае она не может быть использована в дальнейшем. Рассматривая обозначение конусности на чертежах следует уделить внимание следующим моментам:

Отображается диаметр большого основания. Рассматриваемая фигура образуется телом вращения, которому свойственен диаметральный показатель. В случае конуса их может быть несколько, а изменение показателя происходит плавно, не ступенчато. Как правило, у подобной фигуры есть больший диаметр, а также промежуточной в случае наличия ступени.
Наносится диаметр меньшего основания. Меньшее основание отвечает за образование требуемого угла.
Рассчитывается длина конуса. Расстояние между меньшим и большим основанием является показателем длины.
На основании построенного изображения определяется угол. Как правило, для этого проводятся соответствующие расчеты. В случае определения размера по нанесенному изображению при применении специального измерительного прибора существенно снижается точность. Второй метод применяется в случае создания чертежа для производства неответственных деталей.

Простейшее обозначение конусности предусматривает также отображения дополнительных размеров, к примеру, справочную. В некоторых случаях применяется знак конусности, который позволяет сразу понят о разности диаметров.

Выделяют достаточно большое количество различных стандартов, которые касаются обозначения конусности. К особенностям отнесем следующее:

Угол может указываться в градусах дробью или в процентах. Выбор проводится в зависимости от области применения чертежа. Примером можно назвать то, что в машиностроительной области указывается значение градуса.
В машиностроительной области в особую группу выделяют понятие нормальной конусности. Она варьирует в определенном диапазоне, может составлять 30, 45, 60, 75, 90, 120°. Подобные показатели свойственны большинству изделий, которые применяются при сборке различных механизмов. При этом выдержать подобные значения намного проще при применении токарного оборудования. Однако, при необходимости могут выдерживаться и неточные углы, все зависит от конкретного случая.
При начертании основных размеров применяется чертежный шрифт. Он характеризуется довольно большим количеством особенностей, которые должны учитываться. Для правильного отображения используется табличная информация.
Для начала указывается значок конусности от которого отводится стрелка и отображается величина. Особенности отображения во многом зависит от того, какой чертеж. В некоторых случаях наносится большое количество различных размеров, что существенно усложняет нанесение конусности. Именно поэтому предусмотрена возможность использования нескольких различных методов отображения подобной информации.

Формула для определения конусности

Провести самостоятельно расчет конусности можно при применении различных формул. Стоит учитывать, что в большинстве случаев показатель указывается в градусах, но может и в процентах – все зависит от конкретного случая. Алгоритм проведения расчетов выглядит следующим образом:

K=D-d/l=2tgf=2i. Данная формула характеризуется тем, что конусность характеризуется двойным уклоном. Она основана на получении значения большого и меньшего диаметра, а также расстояния между ними. Кроме этого определяется угол.
Tgf=D/2L. В данном случае требуется протяженность отрезка, который связывает большой и малый диаметр, а также показатель большого диаметра.
F=arctgf. Эта формула применяется для перевода показателя в градусы. Сегодня в большинстве случаев применяются именно градусы, так как их проще выдерживать при непосредственном проведении построений. Что касается процентов, то они зачастую указываются для возможности расчета одного из диаметров. К примеру, если соотношение составляет 20% и дан меньший диаметр, то можно быстро провести расчет большого.

Как ранее было отмечено, конусность 1:5 и другие показатели стандартизированы. Для этого применяется ГОСТ 8593-81.

На чертеже вычисления не отображаются. Как правило, для этого создается дополнительная пояснительная записка. Вычислить основные параметры довольно просто, в некоторых случаях проводится построение чертежа, после чего измеряется значение угла и другие показатели.

КАЛЬКУЛЯТОР КОНУСНОСТИ

Конусность — это отношение разности диаметров к длине(высоте) конуса. Например, конусноть 1:10 означает, что D — d = 1, а L(h) = 10. А конусноть 7:24 означает, что D — d = 7, а L(h) = 24.

Рисунок 1 — Схема конуса.

Конус — геометрическое тело, которое получается путем вращением прямой линии (образующей конуса), расположенной под углом к оси вращения. Конусность измерить нельзя. Измеряют угол, который соответсвует конкретной конусности. Например, угол конусности 1 : 10 будет равен 5° 43′ 29.3″ (5 градусам 43 минутам 29.3 секундам). 1 угол содержит 60 минут, а 1 минута содержит 60 секунд. На производстве углы измеряют инструментом, который называется угломер.

С помощью калькулятора на данной странице вы сможете рассчитать любую конусность. Часто это бывает нужно, когда на чертеже не хватает размеров, а чертеж не в векторном формате. Так же, например, необходима бывает индентификация конусности на существующем изделии (штифт, инструмент и др.). Нормальные конусности представлены в ГОСТ 8593-81. Инструментальные конусности представлены в ГОСТ 25557-2006. Среди инструментальных конусов выделяются конуса Морзе. В российских стандартах обозначаются КМ0-КМ7 (КМ7 не рекомендован к применению). В немецких стандартах МК0-МК7. В английских стандартах МТ0-МТ7. При расчете используются следующие буквенные обозначения:

D — наибольшее основание конуса;
d — наименьшее основание конуса;
L — длина конуса;
α — угол конуса;
α/2- угол уклона.

Таблица 1 — Конусности нормальные и инструментальные

Конусность	Угол конуса	Угол уклона
1 : 500	0° 6′ 52.5″	0° 3′ 25.25″
1 : 200	0° 17′ 11.3″	0° 8′ 35.65″
1 : 100	0° 34′ 22.6″	0° 17′ 11.3″
1 : 50	1° 8′ 45.2″	0° 34′ 22.6″
1 : 30	1° 54′ 34.9″	0° 57′ 17.45″
1 : 20	2° 51′ 51.1″	1° 25′ 55.55″
1 : 15	3° 49′ 5.9″	1° 54′ 32.95″
1 : 12	4° 46′ 18.8″	2° 23′ 9.4″
1 : 10	5° 43′ 29.3″	2° 51′ 44.65″
1 : 8	7° 9′ 9.6″	3° 34′ 34.8″
1 : 7	8° 10′ 16.4″	4° 5′ 8.2″
1 : 6	9° 31′ 38.2″	4° 45′ 49.1″
1 : 5	11° 25′ 16.3″	5° 42′ 38.15″
1 : 4	14° 15′ 0.1″	7° 7′ 30.05″
1 : 3	18° 55′ 28.7″	9° 27′ 44.35″
1 : 1.866025	30° 0′ 0″	15° 0′ 0″
1 : 1.207107	45° 0′ 0″	22° 30′ 0″
1 : 0.866025	60° 0′ 0″	30° 0′ 0″
1 : 0.651613	75° 0′ 0″	37° 30′ 0″
1 : 0.500000	90° 0′ 0″	45° 0′ 0″
1 : 0.288675	120° 0′ 0″	60° 0′ 0″
Метрический конус
1 : 20	2° 51′ 51.1″	1° 25′ 55.55″
Конус Морзе №0
1 : 19.212	1° 29′ 27″	0° 44′ 43.5″
Конус Морзе №1
1 : 20.047	1° 25′ 43″	0° 42′ 51.5″
Конус Морзе №2
1 : 20.020	1° 25′ 50″	0° 42′ 55″
Конус Морзе №3
1 : 19.992	1° 26′ 16″	0° 43′ 8″
Конус Морзе №4
1 : 19.254	1° 29′ 15″	0° 44′ 37.5″
Конус Морзе №5
1 : 19.002	1° 30′ 26″	0° 45′ 13″
Конус Морзе №6
1 : 19.18	1° 29′ 36″	0° 44′ 48″
Конусность 7:24
1 : 3.42857143	16° 35′ 39″	8° 17′ 49″
Конусность резьб конических
1 : 16	3° 34′ 48″	1° 47′ 24″

Конус 1:500 и 1:200 применяют для изготовления крепежных деталей для неразъемных соединений, подвергающихся вибрациям и ударной переменной нагрузке, конических оправок. Конус 1:100 применяют для изготовления крепежных деталей для неразъемных соединений, подвергающихся вибрациям и спокойной переменной нагрузке, клиновых шпонок, конических оправок. Конус 1:50 применяют для изготовления конических штифтов, установочных шпилек, насадных рукояток. Конус 1:30 применяют для изготовления конусов шеек шпинделей. Конус 1:20 применяют для изготовления метрических конусов в шпинделях станков, оправок. Конус 1:16 применяют для изготовления конических резьбовых соединений метрических и дюймовых. Конус 1:15 применяют для изготовления конических соединений деталей при осевых нагрузках, соединений поршней со штоками. Конус 1:12 применяют для изготовления конических закрепительных втолок шарико- и роликоподшипников. Конус 1:10 применяют для изготовления конических соединений деталей при нагрузках, перпендикулярных и параллельных оси, концов валов электрических и других машин, регулируемых втулок подшипников шпинделей. Конус 1:7 применяют для кранов в арматуростроении. Конус 1:5 и 1:3 применяют для изготовления легкоразъемных конических соединений при нагрузках, перпендикулярных оси, конических фрикционных муфт. Конус 1:1.5 применяют для изготовления тяжелых винтовых трубных соединений с коническим уплотнением. Конус 30° применяют для изготовления фрикционных муфт приводов, зажимных цанг, головок шинных болтов. Конус 60° применяют для изготовления центровых отверстий. Конус 75° применяют для изготовления внутренних конусов нажимных гаек в соединениях труб высокого давления, наружных центров инструментов диаметром до 10 мм. Конус 90° применяют для изготовления концов обрабатываемых валов и валиков, конусов вентилей и клапанов, центровых отверстий для тяжелых работ, потайных головок заклепок диаметром 1 — 10 мм. Конус 100° применяют для изготовления винтов по дереву. Конус 120° применяют для изготовления потайных головок заклепок диаметром 2 — 5 мм, внутренних фаскок резьбовых отверстий, конусов под набивку сальников, дроссельных клапанов.

Рисунок 2 — Обозначение конусности на чертеже.

Значок конуса обязательно должен быть направлен в сторону уменьшения диаметра.
Определение угла конуса размеры конуса D
d

L
угол конуса α разложение угла конуса °
‘

«
угол уклона α/2 разложение угла уклона °
‘

«
определение малого диаметра 1 : D L малый диаметр d
Посмотреть какие настройки токарного станка для обработки конуса существуют можно на этой странице .

Угол конуса

Важным показателем при построении различных чертежей считается угол конуса. Он определяется соотношение большого диаметра к меньшему. Высчитывается этот показатель по следующим причинам:

На момент обработки мастер должен учитывать этот показатель, так как он позволяет получить требуемое изделие с высокой точностью размеров. В большинстве случаев обработка проводится именно при учете угла, а не показателей большого и малого диаметра.
Угол конуса рассчитывается на момент разработки проекта. Этот показатель наносится на чертеж или отображается в специальной таблице, которая содержит всю необходимую информацию. Оператор станка или мастер не проводит расчеты на месте производства, вся информация должна быть указана в разработанной технологической карте.
Проверка качества изделия зачастую проводится по малому и большему основанию, но также могут применяться инструменты, по которым определяется показатель конусности.

Как ранее было отмечено, в машиностроительной области показатель стандартизирован. В другой области значение может существенно отличаться от установленных стандартов. Некоторые изделия характеризуются ступенчатым расположение поверхностей. В этом случае провести расчеты достаточно сложно, так как есть промежуточный диаметр.

Что такое уклон?

Как ранее было отмечено, довольно важным показателем можно считать уклон. Он представлен линией, которая расположена под углом к горизонту. Если рассматривать конусность на чертеже, то она представлена сочетанием двух разнонаправленных уклонов, которые объединены между собой.

Понятие уклона получило весьма широкое распространение. В большинстве случаев для его отображения проводится построение треугольника с определенным углом.

Две вспомогательные стороны применяются для расчета угла, которые и определяет особенности наклона основной поверхности.

Конусность и уклон: построение, расчет, обозначение

Как определить уклон

Для определения уклона достаточно воспользоваться всего одной формулой. Как ранее было отмечено, существенно упростить задачу можно при построении прямоугольного треугольника. Среди особенностей подобной работы отметим следующие моменты:

Определяется начальная и конечная точка отрезка. В случае построения сложной фигуры она определяется в зависимости от особенностей самого чертежа.
Проводится вертикальная линия от точки, которая находится выше. Она позволяет построить прямоугольный треугольник, который часто используется для отображения уклона.
Под прямым углом проводится соединение вспомогательной линии с нижней точкой.
Угол, который образуется между вспомогательной и основной линией в нижней точке высчитывается для определения наклона.

Формула, которая требуется для вычисления рассматриваемого показателя указывалась выше. Стоит учитывать, что полученный показатель также переводится в градусы.

Особенности построения уклона и конусности

Область черчения развивалась на протяжении достаточно длительного периода. Она уже много столетий назад применялась для передачи накопленных знаний и навыков. Сегодня изготовление всех изделия может проводится исключительно при применении чертежей. При этом ему больше всего внимания уделяется при наладке массового производства. За длительный период развития черчения были разработаны стандарты, которые позволяют существенно повысить степень читаемости всей информации. Примером можно назвать ГОСТ 8593-81. Он во многом характеризует конусность и уклон, применяемые методы для их отображения. Начертательная геометрия применяется для изучения современной науки, а также создания различной техники. Кроме этого, были разработаны самые различные таблицы соответствия, которые могут применяться при проведении непосредственных расчетов.

Построение уклона и конусности

Провести построение уклона и конусности достаточно просто, только в некоторых случаях могут возникнуть серьезные проблемы. Среди основных рекомендаций отметим следующее:

Проще всего отображать нормальные конусности, так как их основные параметры стандартизированы.
В большинстве случаев вводной информацией при создании конусности становится больший и меньший диаметр, а также промежуточное значение при наличии перепада. Именно поэтому они откладываются первыми с учетом взаимного расположения, после чего проводится соединение. Линия, которая прокладывается между двумя диаметрами и определяет угол наклона.
С углом наклона при построении возникает все несколько иначе. Как ранее было отмечено, для отображения подобной фигуры требуется построение дополнительных линий, которые могут быть оставлены или убраны. Существенно упростить поставленную задачу можно за счет применения инструментов, которые позволяют определить угол наклона, к примеру, транспортир.

На сегодняшний день, когда компьютеры получили весьма широкое распространение, отображение чертежей также проводится при применении специальных программ. Их преимуществами можно назвать следующее:

Простоту работы. Программное обеспечение создается для того, чтобы существенно упростить задачу по созданию чертежа. Примером можно назвать отслеживание углов, размеров, возможность зеркального отражения и многое другое. При этом не нужно обладать большим набором различных инструментов, достаточно приобрести требуемую программу и подобрать подходящий компьютер, а также устройство для печати. За счет появления программного обеспечения подобного типа построение конусности и других поверхностей существенно упростилось. Именно поэтому на проведение построений уходит намного меньше времени нежели ранее.
Высокая точность построения, которая требуется в случае соблюдения масштабов. Компьютер не допускает погрешности, если вся информация вводится точно, то отклонений не будет. Этот момент наиболее актуален в случае создания проектов по изготовлению различных сложных изделий, когда отобразить все основные размеры практически невозможно.
Отсутствие вероятности допущения ошибки, из-за которой линии будут стерты. Гриф может растираться по поверхности, и созданный чертеж в единственном экземпляре не прослужит в течение длительного периода. В случае использования электронного варианта исполнения вся информация отображается краской, которая после полного высыхания уже больше не реагирует на воздействие окружающей среды.
Есть возможность провести редактирование на любом этапе проектирования. В некоторых случаях в разрабатываемый чертеж приходится время от времени вносить изменения в связи с выявленными ошибкам и многими другим причинами. В случае применения специального программного обеспечения сделать это можно практически на каждом этапе проектирования.
Удобство хранения проекта и его передачи. Электронный чертеж не обязательно распечатывать, его можно отправлять в электронном виде, а печать проводится только при необходимости. При этом вся информация может копироваться много раз.

Процедура построения при применении подобных программ характеризуется достаточно большим количеством особенностей, которые нужно учитывать. Основными можно назвать следующее:

Программа при построении наклонных линий автоматически отображает угол. Проведенные расчеты в этом случае позволяют проводить построение даже в том случае, если нет информации об большом или малом, промежуточном диаметре. Конечно, требуется информация, касающаяся расположения диаметров относительно друг друга.
Есть возможность использовать дополнительные инструменты, к примеру, привязку для построения нормальной конусности. За счет этого существенно прощается поставленная задача и ускоряется сама процедура. При черчении от руки приходится использовать специальные инструменты для контроля подобных параметров.
Длина всех линий вводится числовым методом, за счет чего достигается высокая точность. Погрешность может быть допущена исключительно при применении низкокачественного устройства для вывода графической информации.
Есть возможность провести замер всех показателей при применении соответствующих инструментов.
Для отображения стандартов используются соответствующие инструменты, которые также существенно упрощают поставленную задачу. Если программа имеет соответствующие настройки, то достаточно выбрать требуемый инструмент и указывать то, какие размеры должны быть отображены. При этом нет необходимости знания стандартов, связанных с отображением стрелок и других линий.

Что такое уклон? Как определить уклон? Как построить уклон? Обозначение уклона на чертежах по ГОСТ.

Уклон. Уклон это отклонение прямой линии от вертикального или горизонтального положения. Определение уклона. Уклон определяется как отношение противолежащего катета угла прямоугольного треугольника к прилежащему катету, то есть он выражается тангенсом угла а. Уклон можно посчитать по формуле i=AC/AB=tga.

Построение уклона. На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки. Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.

Обозначение уклона на чертежах. Обозначение уклонов на чертеже выполняется в соответствии с ГОСТ 2.307—68. На чертеже указывают величину уклона с помощью линии-выноски. На полке линии-выноски наносят знак и величину уклона. Знак уклона должен соответствовать уклону определяемой линии, то есть одна из прямых знака уклона должна быть горизонтальна, а другая должна быть наклонена в ту же сторону, что и определяемая линия уклона. Угол уклона линии знака примерно 30°.

Онлайн-калькулятор объема конуса

Общее определение конуса
Конус – это тело, образованное совокупностью всех лучей, исходящих из точки пространства и пересекающих плоскость.

Точка, из которой лучи исходят, получила название вершины конуса. В случае, когда основанием конуса является многоугольник, он превращается в пирамиду.

Рассмотрим некоторые важные понятия.

Образующей конуса называется отрезок, который соединяет любую точку границы основания конуса, с его вершиной. Высотой конуса является перпендикуляр, который опущен из вершины к основанию тела.

Конус бывает нескольких типов:

Прямой, если его основание – одна из таких фигур, как эллипс или круг. Обязательным условием является проецирование вершины конуса в центр основания.

Косой – у него центр фигуры, которая находится в основании, не совпадает с проекцией вершины на это самое основание.

Круговой – отталкиваясь от названия, понятно, что в его основании лежит круг.

Усеченный – область конуса, лежащая между основанием и сечением плоскости, которая параллельна основанию и пересекает данный конус.

Что такое конусность? Формула для расчёта конусности. Обозначение конусности на чертежах.

Конусность. Конусностью называется отношение диаметра основания конуса к высоте. Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h.

Обозначение конусности на чертежах. Форму и величину конуса определяют нанесением трех из перечисленных размеров: 1) диаметр большого основания D; 2) диаметр малого основания d; 3) диаметр в заданном поперечном сечении Ds , имеющем заданное осевое положение Ls; 4) длина конуса L; 5) угол конуса а; 6) конусность с . Также на чертеже допускается указывать и дополнительные размеры, как справочные.

Размеры стандартизованных конусов не нужно указывать на чертеже. Достаточно на чертеже привести условное обозначение конусности по соответствующему стандарту.

Конусность, как и уклон, может быть указана в градусах, дробью (простой, в виде отношения двух чисел или десятичной), в процентах. Например, конусность 1:5 может быть также обозначена как отношение 1:5, 11°25’16», десятичной дробью 0,2 и в процентах 20. Для конусов, которые применяются в машиностроении, OCT/BKC 7652 устанавливает ряд нормальных конусностей. Нормальные конусности — 1:3; 1:5; 1:8; 1:10; 1:15; 1:20; 1:30; 1:50; 1:100; 1:200. Также в могут быть использованы — 30, 45, 60, 75, 90 и 120°.

Выкройка для конуса

Главная > Геометрия > Выкройка для конуса

19.11.2012 // Владимир Трунов

Построение выкройки для конуса — дело нехитрое. Рассмотрим два случая: для полного конуса и для усеченного. На картинке (кликните, чтобы увеличить) показаны эскизы таких конусов и их выкроек. (Сразу замечу, что речь здесь пойдет только о прямых конусах с круглым основанием. Конусы с овальным основанием и наклонные конусы рассмотрим в следующих статьях).

Полный конус

Обозначения:

— диаметр основания конуса;
— высота конуса;
— радиус дуги выкройки;
— центральный угол выкройки.

Параметры выкройки рассчитываются по формулам: ; ; где .

Усеченный конус

Обозначения:

— диаметр большего основания конуса;
— диаметр меньшего основания конуса;
— высота конуса;
— радиус внешней дуги выкройки;
— радиус внутренней дуги выкройки;
— центральный угол выкройки.

Формулы для вычисления параметров выкройки: ; ; ; где . Заметим, что эти формулы подойдут и для полного конуса, если мы подставим в них .

Угол при вершине конуса

Иногда при построении конуса принципиальным является значение угла при его вершине (или при мнимой вершине, если конус усеченный). Самый простой пример — когда нужно, чтобы один конус плотно входил в другой. Обозначим этот угол буквой (см. картинку). В этом случае мы можем его использовать вместо одного из трех входных значений: , или . Почему «вместо«, а не «вместе«? Потому что для построения конуса достаточно трех параметров, а значение четвертого вычисляется через значения трех остальных. Почему именно трех, а не двух и не четырех — вопрос, выходящий за рамки этой статьи. Таинственный голос мне подсказывает, что это как-то связано с трехмерностью объекта «конус». (Сравните с двумя исходными параметрами двухмерного объекта «сегмент круга», по которым мы вычисляли все остальные его параметры в статье Геометрия круга.)

Ниже приведены формулы, по которым определяется четвертый параметр конуса, когда заданы три.

Заданы ; тогда .
Заданы ; тогда .
Заданы ; тогда .
Заданы ; тогда .

Методы построения выкройки

Вычислить значения на калькуляторе и построить выкройку на бумаге (или сразу на металле) при помощи циркуля, линейки и транспортира.
Занести формулы и исходные данные в электронную таблицу (например, Microsoft Exel). Полученный результат использовать для построения выкройки при помощи графического редактора (например, CorelDRAW).
использовать мою программу Cones, которая нарисует на экране и выведет на печать выкройку для конуса с заданными параметрами. Эту выкройку можно сохранить в виде векторного файла и импортировать в CorelDRAW.

Не параллельные основания

Что касается усеченных конусов, то программа Cones пока строит выкройки для конусов, имеющих только параллельные основания. Для тех, кто ищет способ построения выкройки усеченного конуса с не параллельными основаниями, привожу ссылку, предоставленную одним из посетителей сайта: Усеченный конус с не параллельными основаниями.

геометрические формулы

В экономике

В контексте экономики угловое решение лучше всего охарактеризовано тем, что наивысшая достижимая кривая безразличия не касается линии бюджета , в этом сценарии потребитель вкладывает весь свой бюджет в покупку как можно большего количества одного товара и ни одного из них. Другие. Когда наклон кривой безразличия больше, чем наклон бюджетной линии, потребитель готов отказаться от товара 1 за единицу товара 2 больше, чем требуется на рынке. Таким образом, следует, что если наклон кривой безразличия строго больше, чем наклон бюджетной линии:

Тогда результатом будет угловое решение, пересекающее ось абсцисс. Обратное также верно для углового решения, полученного в результате пересечения оси y.

Некоторые примеры

Реальные примеры углового решения возникают, когда кто-то говорит: «Я бы не стал покупать это ни за какую цену», «Зачем мне покупать X, когда Y дешевле» или «Я сделаю X независимо от стоимости», это может быть для любое количество причин, например, плохое впечатление от бренда, лояльность к определенному бренду / товару или наличие более дешевой версии того же товара. Другой пример – политика «нулевой терпимости» или родители, которые не желают подвергать своих детей какому-либо риску, независимо от того, насколько малы и какие преимущества могут быть. «Нет ничего важнее безопасности моего ребенка» – это решающее решение в ее отказе признать, что возможны компромиссы. Термин «угловое решение» иногда используется экономистами в более разговорной манере для обозначения такого рода ситуаций. Другая ситуация, в которой может возникнуть угловое решение, – это когда два рассматриваемых товара являются идеальной заменой. Слово «угол» относится к тому факту, что если построить график задачи максимизации, оптимальная точка будет находиться в «углу», созданном бюджетным ограничением и одной осью.

По математике

Угловое решение – это случай, когда «лучшее» решение (т. Е. Максимизация прибыли, полезности или любой другой искомой ценности) достигается не на основе экономически эффективной максимизации связанных количеств, а, скорее, на основе граничных условий грубой силы. Такому решению не хватает математической элегантности , и большинство примеров характеризуются внешними принудительными условиями (такими как «переменные x и y не могут быть отрицательными»), которые выводят фактические локальные экстремумы за пределы допустимых значений.

Другой технический способ заявить об этом состоит в том, что угловое решение – это решение проблемы минимизации или максимизации, где неугловое решение недопустимо, то есть не находится в области. Вместо этого решение представляет собой угловое решение на оси, где либо x, либо y равны нулю. Например, из приведенного выше примера в экономике, если максимальная полезность двух товаров достигается, когда количество товаров x и y равно (−2, 5), а полезность подчиняется ограничению, x и y больше или равно 0 (нельзя потреблять отрицательное количество товаров), как это обычно бывает, то фактическим решением проблемы будет угловое решение, где x = 0.

В теории потребителей

Более обычное решение будет лежать в ненулевой внутренней части в точке касания между целевой функцией и ограничением. Например, в теории потребителей целевая функция – это карта кривой безразличия ( функция полезности ) потребителя. Бюджетная строка является ограничением. В обычном случае ограниченная полезность максимизируется при ограничении бюджета со строго положительными количествами, потребляемыми обоими товарами. Однако для углового решения полезность максимизируется в точке на одной оси, где бюджетное ограничение пересекает наивысшую достижимую кривую безразличия при нулевом потреблении для одного товара со всем доходом, используемым для другого товара. Кроме того, диапазон более низких цен на товар с начальным нулевым потреблением может оставить объем спроса неизменным на уровне нуля, а не увеличивать его, как в более обычном случае.

Как найти угловое решение

Графически

Чтобы найти угловое решение графически, нужно сместить кривую безразличия в сторону увеличения полезности. Если между кривой безразличия и линией бюджета достигается точка касания, то углового решения у вас нет, это внутреннее решение. Если вы не найдете точку касания в домене, тогда кривая безразличия, максимизирующая полезность для данного бюджетного ограничения, будет на пересечении между осью x или y (в зависимости от того, является ли наклон кривой безразличия строго больше или меньше чем крутизна бюджетного ограничения) – это угловое решение.

Математически

Для математического решения углового решения необходимо применить метод Лагранжа с ограничениями неотрицательности x ≥ 0 и y ≥ 0.

Смотрите также

Кривая безразличия: раздел предположений
Интерьерное решение (оптимизация)

использованная литература

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 ноября 2022 года; проверки требуют 2 правки.

У этого термина существуют и другие значения, см. Конус (значения).

Ко́нус (через нем. Konus и лат. cōnus, от др.-греч. κώνος^[1] — «сосновая шишка»^[2]) — поверхность, образованная в пространстве множеством лучей (образующих конуса), соединяющих все точки некоторой плоской кривой (направляющей конуса) с данной точкой пространства (вершиной конуса)^[3].

Если направляющая конуса — замкнутая кривая, то коническая поверхность служит границей пространственного тела, которое также называют «конусом» (см. рисунок), а внутренность этой кривой называют «основанием конуса», если основание конуса представляет собой многоугольник, такой конус является пирамидой.

Иногда вместо лучей рассматривают прямые, тогда получается двойной конус, состоящий из двух симметричных относительно вершины частей.

Конус и связанные с ним конические сечения играют большую роль в математике, астрономии и других науках.

Связанные определения[править | править код]

Боковая поверхность конуса — объединение образующих конуса; образующая поверхность конуса является конической поверхностью.
Высота конуса — отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка).
Угол раствора конуса — угол между двумя противоположными образующими (угол при вершине конуса, внутри конуса).
Конусность — соотношение высоты и диаметра основания конуса.

Типы конусов[править | править код]

Прямой круговой конус
Прямой и косой круговые конусы с равным основанием и высотой: их объём одинаков
Усечённый прямой круговой конус

Прямой конус — конус, основание которого имеет центр симметрии (например, является кругом или эллипсом) и ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром; при этом прямая, соединяющая вершину и центр основания, называется осью конуса.
Косой (или наклонный) конус — конус, у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии.
Круговой конус — конус, основание которого является кругом.
Конус вращения, или прямой круговой конус (часто под конусом подразумевают именно его) — конус, который можно получить вращением (то есть тело вращения) прямоугольного треугольника вокруг прямой, содержащей катет треугольника (эта прямая является осью конуса).
Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом: последние два имеют бесконечный объём.
Усечённый конус или конический слой — часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием.
Равносторонний конус — конус вращения, образующая которого равна диаметру основания ^[4].

Свойства[править | править код]

Если площадь основания конечна, то объём конуса также конечен и равен трети произведения высоты на площадь основания.

где S — площадь основания, H — высота. Таким образом, все конусы, опирающиеся на данное основание (конечной площади) и имеющие вершину, находящуюся на данной плоскости, параллельной основанию, имеют равный объём, поскольку их высоты равны.

Центр тяжести любого конуса с конечным объёмом лежит на четверти высоты от основания.
Телесный угол при вершине прямого кругового конуса равен

где α — угол раствора конуса.

Площадь боковой поверхности прямого кругового конуса равна

а в общем случае

${displaystyle S={frac {tl}{2}},}$

где R — радиус основания, ${displaystyle t={sqrt {R^{2}+H^{2}}}}$

— длина образующей,

— длина границы основания.

Полная площадь поверхности (то есть сумма площадей боковой поверхности и основания) равна

для прямого кругового конуса и

${displaystyle S={frac {tl}{2}}+S_{text{ос}},}$

для произвольного, где ${displaystyle S_{text{ос}}}$

— площадь основания.

Объём кругового (не обязательно прямого) конуса равен

$V={1 over 3}pi R^{2}H.$

Для усечённого кругового конуса (не обязательно прямого) объём равен:

${displaystyle V={1 over 3}pi H(R^{2}+Rr+r^{2}),}$

где

— радиусы соответственно нижнего и верхнего оснований,

— высота от плоскости нижнего основания,до верхнего основания.

Для произвольного усечённого конуса (не обязательно прямого и кругового) объём равен:

${displaystyle V={1 over 3}(H_{2}S_{2}-H_{1}S_{1}),}$

где $S_{1}$

и $S_{2}$

— площади соответственно верхнего (ближнего к вершине) и нижнего оснований, H_1

— расстояния от плоскости соответственно верхнего и нижнего основания до вершины.

Пересечение плоскости с прямым круговым конусом является одним из конических сечений (в невырожденных случаях — эллипсом, параболой или гиперболой, в зависимости от положения секущей плоскости).

Уравнение прямого кругового конуса[править | править код]

Уравнения, задающие боковую поверхность прямого кругового конуса с углом раствора 2Θ, вершиной в начале координат и осью, совпадающей с осью Oz:

В сферической системе координат с координатами (r, φ, θ):

В цилиндрической системе координат с координатами (r, φ, z):

или

В декартовой системе координат с координатами (x, y, z):

$z=pm {sqrt {x^{2}+y^{2}}}cdot operatorname {ctg}Theta .$

Это уравнение в каноническом виде записывается как

${frac {x^{2}}{a^{2}}}+{frac {y^{2}}{a^{2}}}-{frac {z^{2}}{c^{2}}}=0,$

где константы a, с определяются пропорцией

Отсюда видно, что боковая поверхность прямого кругового конуса представляет собой поверхность второго порядка (она носит название коническая поверхность). В общем виде коническая поверхность второго порядка опирается на эллипс; в подходящей декартовой координатной системе (оси Ох и Оу параллельны осям эллипса, вершина конуса совпадает с началом координат, центр эллипса лежит на оси Oz) её уравнение имеет вид

${frac {x^{2}}{a^{2}}}+{frac {y^{2}}{b^{2}}}-{frac {z^{2}}{c^{2}}}=0,$

причём a/c и b/c равны полуосям эллипса. В наиболее общем случае, когда конус опирается на произвольную плоскую поверхность, можно показать, что уравнение боковой поверхности конуса (с вершиной в начале координат) задаётся уравнением

где функция

является однородной, то есть удовлетворяющей условию $f(alpha x,alpha y,alpha z)=alpha ^{n}f(x,y,z)$

для любого действительного числа α.

Развёртка[править | править код]

Развёртка прямого кругового конуса

Прямой круговой конус как тело вращения образован прямоугольным треугольником, вращающимся вокруг одного из катетов, где h — высота конуса от центра основания до вершины — является катетом прямоугольного треугольника, вокруг которого происходит вращение. Второй катет прямоугольного треугольника r — радиус в основании конуса. Гипотенузой прямоугольного треугольника является l — образующая конуса.

В создании развёртки конуса могут использоваться всего две величины r и l. Радиус основания r определяет в развертке круг основания конуса, а сектор боковой поверхности конуса определяет образующая боковой поверхности l, являющаяся радиусом сектора боковой поверхности. Угол сектора varphi в развёртке боковой поверхности конуса определяется по формуле:

φ = 360°·(r/l).

Вариации и обобщения[править | править код]

См. также[править | править код]

Коническая поверхность
Коническое сечение
Конус (топология)
Световой конус

Примечания[править | править код]

↑ Этимологический словарь русского языка Макса Фасмера
↑ «I κῶνος»
↑ Математический энциклопедический словарь, 1988, с. 288.
↑ Математический справочник. Дата обращения: 22 мая 2020. Архивировано 2 декабря 2020 года.

Литература[править | править код]

Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — 2-е изд. — М.: Наука, 1970. — 720 с.
Конус // Математический энциклопедический словарь. — М.: Советская энциклопедия, 1988. — С. 288. — 847 с.

Источник

Онлайн-калькулятор

Рассмотрим некоторые важные понятия.

Конус бывает нескольких типов:

Круговой – отталкиваясь от названия, понятно, что в его основании лежит круг.

Свойства кругового конуса

Выделяют несколько особенностей, которыми обладает фигура данного типа:

Образующие кругового конуса равны друг другу.
Чтобы найти центр тяжести фигуры, нужно её высоту поделить на четыре части.
Место пересечения плоскости сечения и основы образует параболу. Если через вершину тела провести плоскость сечения, то получится равнобедренный треугольник.

Интересный факт!

Если вращать прямоугольный треугольник вокруг одного из катетов, то получится конус. При этом важно, чтобы угол вращения был не менее 360 градусов.

Связанные определения для конуса

Образующая конуса. Отрезок, соединяющий вершину и границу основания, называется образующей конуса.

Коническая поверхность. Образующая поверхность конуса является конической поверхностью.

Угол раствора конуса. Угол раствора конуса – угол между двумя противоположными образующими (угол при вершине конуса, внутри конуса).

Косой (наклонный) конус. Косой (наклонный) конус – конус, у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии.

Круговой конус. Круговой конус – конус, основание которого является кругом.

Виды конусов

Прямой конус – имеет симметричное основание. Ортогональная проекция вершины данной фигуры на плоскость основания совпадает с центром этого основания.
Косой (наклонный) конус – ортогональная проекция вершины фигуры на ее основание не совпадает с центром этого основания.
Усеченный конус (конический слой) – часть конуса, которая остается между его основанием и секущей плоскостью, параллельной данному основанию.
Круговой конус – основанием фигуры является круг. Также бывают: эллиптический, параболический и гиперболический конусы.
Равносторонний конус – прямой конус, образующая которого равняется диаметру его основания.

Объем конуса

Объем конуса

равен трети от произведению площади его основания на высоту.

Формулы объема конуса:

где V – объем конуса, So – площадь основания конуса, R – радиус основания конуса, h – высота конуса, π = 3.141592.

Вариации и обобщения

В алгебраической геометрии конус
— это произвольное подмножество K {displaystyle K} векторного пространства V {displaystyle V} над полем F {displaystyle F} , для которого для любого λ ∈ F {displaystyle lambda in F} λ K = K . {displaystyle lambda K=K.}
В топологии конус над топологическим пространством X
есть фактор-пространство X × [ 0 , ∞ ) {displaystyle Xtimes [0,infty )} по отношению эквивалентности ( x , 0 ) ∼ ( y , 0 ) . {displaystyle (x,0)sim (y,0).}

Объем конуса через радиус

Данный треугольник

для получения конуса должен вращаться вокруг одного из своих
катетов
, который является не только осью вращения, но и высотой конуса.
Второй
же катет становится радиусом полученной в результате вращения окружности-основания конуса, а гипотенуза будет апофемой (высотой опущенной под прямым углом к линии окружности, а не центру).

Технически взаимосвязь конуса

с цилиндром идентична взаимосвязи пирамиды с кубом (параллелепипедом), единственное, что вывод
формулы
проходит через отношения интегралов их сферических углов, но тем не менее, он точно также как и пирамида занимает одну треть цилиндра, в который он может быть вписан.

Поэтому его объем

равен произведению площади основания на высоту, деленному на три, или произведению числом
π
на квадрат радиуса и высоту, деленному на три.

Определение конуса

Далее мы будем рассматривать самый распространенный вид конуса – прямой круговой. Остальные возможные варианты фигуры перечислены в последнем разделе публикации.

Итак, прямой круговой конус – это трехмерная геометрическая фигура, полученная путем вращения прямоугольного треугольника вокруг одного из своих катетов, который в данном случае будет являться осью фигуры. Ввиду этого иногда такой конус называют конусом вращения.

Конус на рисунке выше получен в результате вращения прямоугольного треугольника ACD (или BCD) вокруг катета CD.

Объем усеченного конуса

Усеченный конус получится, если в конусе провести сечение, параллельное основанию. Тело ограниченное этим сечением, основанием и боковой поверхностью конуса называется усеченным конусом.

Первый способ вычисления объема усеченного конуса

Объем усеченного конуса вычисляется по формуле:

[ LARGE V = frac{1}{3} left( Hcdot S_2 + h cdot s_1 right) ]

где: V – объем конуса h – расстояния от плоскости верхнего основания до вершины H – расстояния от плоскости нижнего основания до вершины S1 – площадь верхнего (ближнего к вершине) основания S2 – площадь нижнего основания

Второй способ вычисления объема усеченного конуса

Объем усеченного конуса вычисляется по формуле:

[ LARGE V = frac{1}{3} pi h left( R^2 + R cdot r + r^2 right) ]

где: V – объем конуса h – высота конуса R – радиус нижнего основания r – радиус верхнего основания

Развёртка

— высота конуса от центра основания до вершины — является катетом прямоугольного треугольника, вокруг которого происходит вращение. Второй катет прямоугольного треугольника
r
— радиус в основании конуса. Гипотенузой прямоугольного треугольника является
l
— образующая конуса.

В создании развёртки конуса могут использоваться всего две величины r

и
l
. Радиус основания
r
определяет в развертке круг основания конуса, а сектор боковой поверхности конуса определяет образующая боковой поверхности
l
, являющаяся радиусом сектора боковой поверхности. Угол сектора φ {displaystyle varphi } в развёртке боковой поверхности конуса определяется по формуле:
φ = 360°·(r
/
l
).

Элементы конуса

Определение. Вершина конуса

– это точка (K), из которой исходят лучи.

Определение. Основание конуса

– это плоскость, образованная в результате пересечения плоской поверхности и всех лучей, исходящих из вершины конуса. У конуса могут быть такие основы, как круг, эллипс, гипербола и парабола.

Определение. Образующей конуса

(L) называется любой отрезок, который соединяет вершину конуса с границей основания конуса. Образующая есть отрезок луча, выходящего из вершины конуса.

Формула. Длина образующей

(L) прямого кругового конуса через радиус R и высоту H (через теорему Пифагора): L2 = R2 + H2

Определение. Направляющая

конуса – это кривая, которая описывает контур основания конуса.

Определение. Боковая поверхность

конуса – это совокупность всех образующих конуса. То есть, поверхность, которая образуется движением образующей по направляющей конуса.

Определение. Поверхность

конуса состоит из боковой поверхности и основания конуса.

Определение. Высота

конуса (H) – это отрезок, который выходит из вершины конуса и перпендикулярный к его основанию.

Определение. Ось

конуса (a) – это прямая, проходящая через вершину конуса и центр основания конуса.

Определение. Конусность (С)

конуса – это отношение диаметра основания конуса к его высоте. В случае усеченного конуса – это отношение разности диаметров поперечных сечений D и d усеченного конуса к расстоянию между ними:

где C – конусность, D – диаметр основания, d – диаметр меньшего основания и h – расстояние между основаниями. Конусность характеризует остроту конуса, то есть, угол наклона образующей к основанию конуса. Чем больше конусность, тем острее угол наклона. угол конуса α будет:

где R – радиус основы, а H – высота конуса.

Определение. Осевое сечение

конуса – это сечение конуса плоскостью, проходящей через ось конуса. Такое сечение образует равнобедренный треугольник, у которого стороны образованы образующими, а основание треугольника – это диаметр основания конуса.

Определение. Касательная плоскость

к конусу – это плоскость, проходящая через образующую конуса и перпендикулярна к осевому сечению конуса.

Определение. Конус, что опирается на круг, эллипс, гиперболу или параболу называется соответственно круговым, эллиптическим, гиперболическим

или
параболическим
конусом (последние два имеют бесконечный объем).

Определение. Прямой

конус – это конус у которого ось перпендикулярна основе. У такого конуса ось совпадает с высотой, а все образующие равны между собой.

Формула. Объём кругового конуса

где R – радиус основы, а H – высота конуса.
Формула. Площадь боковой поверхности

(Sb) прямого конуса через радиус R и длину образующей L: Sb = πRL

Формула. Общая площадь поверхности

(Sp) прямого кругового конуса через радиус R и длину образующей L: Sp = πRL + πR2

Определение. Косой (наклонный)

конус – это конус у которого ось не перпендикулярна основе. У такого конуса ось не совпадает с высотой.

Формула. Объём любого конуса

где S – площадь основы, а H – высота конуса.

Определение. Усеченный

конус – это часть конуса, которая находится между основанием конуса и плоскостью сечения, параллельная основе.

Формула. Объём усеченного конуса

где S1 и S2 – площади меньшей и большей основы соответственно, а H и h – расстояние от вершины конуса до центра нижней и верхней основы соответственно.

Основные элементы конуса

R – радиус круга, являющегося основанием конуса. Центр круга – точка D, диаметр – отрезок AB.
h (CD) – высота конуса, одновременно являющаяся осью фигуры и катетом прямоугольных треугольников ACD или BCD.
Точка C – вершина конуса.
l (CA, CB, CL и CM) – образующие конуса; это отрезки, соединяющие вершину конуса с точками на окружности его основания.
Осевое сечение конуса – это равнобедренный треугольник ABC, который образуется в результате пересечения конуса плоскостью проходящей через его ось.
Поверхность конуса – состоит из его боковой поверхности и основания. Формулы для расчета площади поверхности, а также объема прямого кругового конуса представлены в отдельных публикациях.

Между образующей конуса, его высотой и радиусом основания есть взаимосвязь (согласно теореме Пифагора):

l2 = h2 + R2

Развёртка конуса – боковая поверхность конуса, развернутая в плоскость; является круговым сектором.

длина дуги сектора равняется длине окружности основания конуса (т.е. 2πR);
α – угол развёртки (или центральный угол);
l – радиус сектора.

Примечание: Основные свойства конуса мы рассмотрели в отдельной публикации.

Основные свойства кругового конуса

1. Все образующие прямого кругового конуса равны между собой.

2. При вращении прямоугольного треугольника вокруг своего катета на 360 ° образуется прямой круговой конус.

3. При вращении равнобедренного треугольника вокруг своей оси на 180 ° образуется прямой круговой конус.

4. В месте пересечения конуса плоскостью, параллельной основанию конуса, образуется круг. (см. Срезанный конус)

5. Если при пересечении плоскость не параллельна основе конуса и не пересекается с основанием, то в месте пересечения образуется эллипс (рис. 3).

6. Если плоскость сечения проходит через основание, то в месте пересечения образуется парабола (рис. 4).

7. Если плоскость сечения проходит через вершину, то в месте пересечения образуется равнобедренный треугольник (см. Осевое сечение).

8. Центр тяжести любого конуса находится на одной четвертой высоты от центра основы.

Определение и элементы конуса

Под конусом понимают тело, состоящее из круга и точки, которая удалена от его поверхности на определённое расстояние.

При этом точка соединяется с основанием посредством проведения лучей, которые называются образующими. Линия, соединяющая центр круга с удалённой точкой, является высотой данной фигуры.

Обратите внимание!

Также существует такое понятие, как ось конуса. Это линия, проходящая через его центр и совпадающая с высотой. Образующие строятся относительно оси.

Хотелось бы рассмотреть ещё несколько понятий по этой теме:

1. Под конусностью понимают отношение диаметра основания фигуры и её высоты:

Важно!

Конусность отвечает за угол наклона образующих. Чем больше данный параметр, тем острее угол.

2. Осевое сечение предполагает наличие плоскости, которая будет рассекать фигуру, проходя через ось:

3. Касательная— это плоскость, которая соприкасается с образующей конуса. При этом важно, чтобы она была перпендикулярна осевому сечению.

Введите радиус основания и высоту конуса

Радиус конуса r

Высота конуса h

Результат

Расчет объема куба, пирамиды, конуса, цилиндра, шара (объема всех фигур).

Объемы фигур

Радиус:

Высота:

Конус – геометрическое тело, которое состоит из круга (основание конуса), точки, не лежащей в плоскости этого круга (вершина конуса), и всех точек, соединяющих вершину конуса с точками основания. Формула объема конуса: , где R – радиус основания, h – высота конуса

Нормальные углы и конусы инструментов

НОРМАЛЬНЫЕ УГЛЫ ( ГОСТ 8908-81 )
Таблица не распространяется на угловые размеры конусов. При выборе углов 1-й ряд следует предпочитать 2-му, а 2-й — 3-му.
НОРМАЛЬНЫЕ КОНУСНОСТИ и УГЛЫ КОНУСОВ ( ГОСТ 8593-81 )
Стандарт распространяется на конусности и углы конусов гладких конических элементов деталей.

Примечание. Значения конусности или угла конуса, указанные в графе «Обозначение конуса», приняты за исходные при расчете других значений, приведенных в таблице. При выборе конусностей или углов конусов ряд 1 следует предпочитать ряду 2.
КОНУСЫ ИНСТРУМЕНТОВ УКОРОЧЕННЫЕ ( ГОСТ 9953-82 )
Стандарт распространяется на укороченные инструментальные конусы Морзе.

*z — наибольшее допускаемое отклонение положения основной плоскости, в которой находится диаметр D от теоретическогот положения. ** размеры для справок.

Обозначение конуса	Конус Морзе	D	D1	d	d1	l1	l2	a, не более	b	c
B7	0	7,067	7,2	6,5	6,8	11,0	14,0	3,0	3,0	0,5
B10 B12	1	10,094 12,065	10,3 12,2	9,4 11,1	9,8 11,5	14,5 18,5	18,0 22,0	3,5 3,5	3,5 3,5	1,0 1,0
B16 B18	2	15,733 17,780	16,8 18,0	14,5 16,2	15,0 16,8	24,0 32,0	29,0 37,0	5,0 5,0	4,0 4,0	1,5 1,5
B22 B24	3	21,793 23,825	22,0 24,1	19,8 21,3	20,5 22,0	40,5 50,5	45,5 55,5	5,0 5,0	4,5 4,5	2,0 2,0
B32	4	31,267	31,6	28,6	—	51,0	57,5	6,5	—	2,0
B45	5	44,399	44,7	41,0	—	64,5	71,0	6,5	—	2,0
Размеры D1 и d являются теоретическими, вытекающими соответственно из диаметра D и номинальных размеров а и l1

КОНУСНОСТЬ НАРУЖНЫХ И ВНУТРЕННИХ КОНУСОВ И КОНУСОВ С РЕЗЬБОВЫМ ОТВЕРСТИЕМ

Обозначение величины конуса	Конусность	Угол конуса 2α
B7 B10, B12 B16, B18 B22, B24 B32 B45	1 : 19,212 = 0,05205 1 : 20,047 = 0,49880 1 : 20,020 = 0,04995 1 : 19,922 = 0,05020 1 : 19,954 = 0,05194 1 : 19,002 = 0,05263	2°58′54″ 2°51′26″ 2°51′41″ 2°52′32″ 2°58′31″ 3°00′53″
угол конуса 2α подсчитан по величине конусности с округлением до 1″.

РЕКОМЕНДУЕМЫЕ РАЗМЕРЫ ЦЕНТРОВОГО ОТВЕРСТИЯ УКОРОЧЕННОГО КОНУСАКОНУСЫ ИНСТРУМЕНТАЛЬНЫЕ МОРЗЕ И МЕТРИЧЕСКИЕ НАРУЖНЫЕ ( ГОСТ 25557-2006 )

Тип конуса	Метрический	Морзе	Метрический
Обозн.	4	6	0	1	2	3	4	5	6	80	100	120	160	200
D	4,0	6,0	9,045	9,065	17,78	23,825	31,267	44,399	63,348	80	100	120	160	200
D1	4,1	6,2	9,2	12,2	18,0	24,1	31,6	44,7	63,8	80,4	100,5	120,6	160,8	201,0
d*	2,9	4,4	6,4	9,4	14,6	19,8	25,9	37,6	53,9	70,2	88,4	106,6	143	179,4
d1	—	—	—	М6	М10	М12	М16	М20	М24	М30	М36	М36	М48	М48
d4 max	2,5	4,0	6,0	9,0	14,0	19,0	25,0	35,7	51,0	67,0	85,0	102,0	138,0	174,0
l min	—	—	—	16,0	24,0	24,0	32,0	40,0	47,0	59,0	70,0	70,0	92,0	92,0
l1	23,0	32,0	50,0	53,5	64,0	81,0	102,5	129,5	182,0	196,0	232,0	268,0	340,0	412,0
l2	25,0	35,0	53,0	57,0	69,0	86,0	109,0	136,0	190,0	204,0	242,0	280,0	356,0	432,0
l11	—	—	—	4,0	5,0	5,5	8,2	10,0	11,5	—	—	—	—	—
* — размер для справок. — угол конусов Морзе №0-№5 соответствует углу укороченных конусов Морзе; №6 — 1:19,180 = 0,05214 — угол метрических конусов — 1:20 = 0,05.

Профиль резьбового отверстия соответствует отверстию центровому форма Р

по
ГОСТ ГОСТ 14034-74
.

В ГОСТ 25557-2006 все размеры центрового отверстия приводятся в общей таблице. Стандарт также определяет размеры пазов канавок и отвестий, необходимых для конструирования конусов, в случае подачи смазочно-охлаждающей жидкости (СОЖ) через инструмент.

В зависимости от конструкции инструментальный хвостовик может иметь соответствующее обозначение:

— внутренний конус с пазом;
BE
— наружный конус с лапкой;
AI
— внутренний конус с отверстием по оси;
АЕ
— наружный конус с резьбовым отверстием по оси;
BIK
— внутренний конус с пазом и отверстием для подачи СОЖ;
ВЕК
— наружный конус с лапкой и отверстием для подачи СОЖ;
AIK
— внутренний конус с отверстием по оси и отверстием для подачи СОЖ;
АЕК
— наружный конус с резьбовым отверстием по оси и отверстием для подачи СОЖ.
КОНУСЫ ИНСТРУМЕНТАЛЬНЫЕ МОРЗЕ И МЕТРИЧЕСКИЕ ВНУТРЕННИЕ ( ГОСТ 25557-2006 )КОНУСЫ ВНУТРЕННИЕ И НАРУЖНЫЕ КОНУСНОСТЬЮ 7 : 24 ( ГОСТ 15945-82 )
Допуски конусов внутренних и наружных конусностью 7:24

по ГОСТ 19860-93.
КОНУСЫ ИНСТРУМЕНТОВ Предельные отклонения угла конуса и допуски формы конусов ( ГОСТ 2848-75 )
Степень точности инструментальных конусов обозначается допуском угла конуса заданной степени точности по ГОСТ 8908-81 и определяется предельными отклонениями угла конуса и допусками формы поверхности конуса, числовые значения которых указаны ниже.

Примечания: 1. Отклонения угла конуса от номинального размера располагав в «плюс» — для наружных конусов, в «минус» — для внутренних. 2. ГОСТ 2848-75 для наружных конусов предусматривает также степени точности АТ4 и АТ5. Допуски по ГОСТ 2848-75 распространяются на конусы инструментов по ГОСТ 25557-2006 и ГОСТ 9953-82.

Пример обозначения конуса Морзе 3, степени точности АТ8:
Морзе 3 АТ8 ГОСТ 25557-2006
То же метрического конуса 160, степени точности АТ7:
Метр. 160 АТ7 ГОСТ 25557-2006
То же укороченного конуса В18, степени точности АТ6:
Морзе В18 АТ6 ГОСТ 9953-82
Похожие документы:

ГОСТ 2848-75 — Конусы инструментов. Допуски. Методы и средства контроля ГОСТ 7343-72 — Конусы инструментов с конусностью 1:10 и 1:7. Размеры ГОСТ 10079-71 — Развертки конические с коническим хвостовиком под конусы Морзе. Конструкция и размеры ГОСТ 22774-77 — Конусы и трубки шлифовальные. Типы и размеры ГОСТ 25548-82 — Основные нормы взаимозаменяемости. Конусы и конические соединения. Термины и определения

Формула площади конуса

Площадь поверхности конуса можно получить, сложив площадь боковой поверхности и площадь основания конуса:

S = Sбок.пов + Sосн = πRL + πR2

Источники

https://studwork.org/spravochnik/matematika/obemy-figur/obem-konusa
https://calcsbox.com/post/formula-obema-konusa.html
https://worksbase.ru/matematika/formuly/37-konus.html
https://ru.onlinemschool.com/math/formula/volume/
https://allcalc.ru/node/36
https://ru.onlinemschool.com/math/formula/cone/
https://www.calc.ru/1430.html
https://MicroExcel.ru/obyom-konusa/
https://www.calc.ru/obyem-konusa.html
https://mnogoformul.ru/obem-konusa-formula-i-raschet-onlayn

Площадь усечённого конуса

Для нахождения данного параметра нужно воспользоваться формулами:

площади боковой поверхности усечённого конуса Sбок;
полной площади усечённой фигуры Sпол, которая равна сумме площадей двух оснований и площади боковой поверхности:

Здесь l — длина образующей, а R и r — радиусы большего и меньшего оснований соответственно.

Источник

Значение конусности

Связанные определения для конуса

Обозначение конусности на чертеже

Формула для определения конусности

КАЛЬКУЛЯТОР КОНУСНОСТИ

Угол конуса

Что такое уклон?

Конусность и уклон: построение, расчет, обозначение

Как определить уклон

Особенности построения уклона и конусности

Построение уклона и конусности

Что такое уклон? Как определить уклон? Как построить уклон? Обозначение уклона на чертежах по ГОСТ.

Онлайн-калькулятор объема конуса

Что такое конусность? Формула для расчёта конусности. Обозначение конусности на чертежах.

Выкройка для конуса

Полный конус

Усеченный конус

Угол при вершине конуса

Методы построения выкройки

Не параллельные основания

Похожие записи

Геометрия круга

Выкройка овального и наклонного конуса

В экономике

По математике

В теории потребителей

Как найти угловое решение

Смотрите также

использованная литература

Связанные определения[править | править код]

Типы конусов[править | править код]

Свойства[править | править код]

Уравнение прямого кругового конуса[править | править код]

Развёртка[править | править код]

Вариации и обобщения[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Онлайн-калькулятор

Свойства кругового конуса

Связанные определения для конуса

Виды конусов

Объем конуса

Вариации и обобщения

Объем конуса через радиус

Определение конуса

Объем усеченного конуса

Первый способ вычисления объема усеченного конуса

Второй способ вычисления объема усеченного конуса

Развёртка

Элементы конуса

Основные элементы конуса

Основные свойства кругового конуса

Определение и элементы конуса

Введите радиус основания и высоту конуса

Нормальные углы и конусы инструментов

Формула площади конуса

Площадь усечённого конуса

Вам также может понравиться

Как найти браслет потерянный на улице

Ребус как составить по чтению

Как найти пару для питомца

Добавить комментарий Отменить ответ