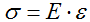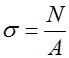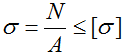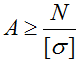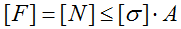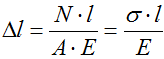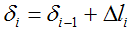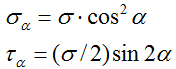Как найти растягивающее усилие - Сайт, где вы сможете решить свои вопросы

Подборка формул для расчета элементов и конструкций на растяжение-сжатие и решения задач сопротивления материалов по расчету нормальных напряжений, деформаций и перемещения сечений стержней при продольном нагружении.

Обозначения в формулах:

σ — нормальные напряжения,
N – внутренняя продольная сила,
A – площадь поперечного сечения,
[σ] – допустимые напряжения,
E – модуль продольной упругости,
ε — относительные деформации.

Закон Гука:

Формула для расчета напряжений в поперечном сечении стержня

Условие прочности (проверочный расчет) при растяжении-сжатии

Расчет минимальной площади поперечного сечения бруса

Расчет допустимой величины внешней растягивающей/сжимающей силы (определение грузоподъемности)

Формула для расчета абсолютных деформаций

Расчет перемещения сечений

Здесь: δ_i — перемещение рассматриваемого сечения,
δ_i-1 — перемещение предыдущего сечения,
Δl_i — деформация участка между указанными сечениями.

Напряжения в наклонных сечениях

Здесь α — угол отклонения сечения от поперечного.

Другие формулы >
Примеры решения задач >
Краткая теория >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Решение задач и лекции по технической механике, теормеху и сопромату

Источник

Под растяжением
понимается такой вид нагружения, при
котором в поперечных сечениях бруса
(стержня) возникают только нормальные
силы, а все прочие внутренние силовые
факторы (поперечные силы, крутящий
и изгибающие моменты) равны нулю.
Сжатие отличается от растяжения только
знаком силы N:
при растяжении
нормальная сила N
направлена
от сечения (см. рис. 2.1), а
при сжатии – к сечению. Поэтому при
анализе внутренних сил сохраняется
единство подхода к вопросам растяжения
и сжатия. Исключение составят длинные
тонкие стержни, для которых сжатие
сопровождается изгибом (см. подразд.
2.7).

Закон Гука.
Многочисленные
наблюдения за поведением твердых
тел показывают, что в подавляющем
большинстве случаев перемещения в
определенных пределах пропорциональны
действующим силам. Впервые в 1676 г.
Гуком был сформулирован закон о том,
что «какова сила, такова и деформация».

В современной
трактовке закон Гука определяет линейную
зависимость между напряжением и
деформацией:

(1.4)

Здесь коэффициент
пропорциональности Е
есть модуль
упругости первого рода, ε – деформация,
которую для однородного стержня можно
определить как

(1.5)

Величину
ε
иногда называют относительным
удлинением стержня
длиной l,
удлинение которого под действием
приложенной силы составило Δl.

Модуль упругости
первого рода
является физической константой
материала; он определяется экспериментально.
Для наиболее часто
встречающихся материалов его значения
приведены в табл. 2.1 (см.
подразд. 2.3).

Удлинение
стержня. Если
в закон Гука вместо напряжения подставить

=
N/S,
а вместо
деформации

, то для стержня, у которого на длине l
внутренняя
нормальная сила постоянная и поперечное
сечение не изменяется, получим выражение
для определения удлинения стержня:

(1.5)

При решении многих
практических задач возникает необходимость
наряду с удлинением, обусловленным
напряжением а, учитывать также удлинения,
связанные с температурным воздействием.

В этом случае
деформацию рассматривают как сумму
силовой и чисто температурной деформации:

(1.6)

где

– коэффициент
температурного расширения материала.
Для однородного стержня, нагруженного
по концам и равномерно нагретого, имеем

(1.7)

Построение эпюр.
График
изменения нормальной силы, напряжений
и перемещений стержня вдоль его оси
называется эпюрой соответственно
нормальных сил, напряжений и перемещений.
Эпюры дают наглядное представление о
законах изменения различных исследуемых
величин. Построение эпюр рассмотрим на
конкретном примере.

Пример 1

Для
бруса, изображенного на рис. 2.3, а,
построить
эпюры внутренних сил, напряжений
и перемещений по длине бруса.

Рис. 2.3

Решение.

1. Выбираем
начало отсчета в неподвижном сечении
(точка О);

положительное
направление оси z
направим
по оси бруса, т.е. вниз.

2.
Определим
реакцию, составив одно уравнение
равновесия:

N₀–
3F
+ F
= 0.
Отсюда
N₀
=2F.

3. Построим
эпюру внутренних сил N.
Для
этого на расстоянии z₁
рассечем

брус
и рассмотрим равновесие нижней части
(рис. 2.3, б):

∑ F_iz
= 0; – N₁
+ F
= 0

Отсюда
N₁=F
,
что справедливо для l
≤ z₁
≤ 3l.
В этих пределах в брусе возникает
растяжение, так как продольная сила N₁
направлена
от сечения.

Теперь
выберем второй участок бруса 0
≤ z₂
≤ l
и рассмотрим равновесие верхней
части (рис. 2.3, в):

∑ F_iz
= 0; N₀
– N₂
= 0; 2F – N₂
= 0

Отсюда
N₂
= 2F. Поскольку
N₂
направлена
к сечению, то брус под действием
сил N₀
и N₂
сжимается.

После
того как определили все внутренние
нормальные силы, переходим к
построению эпюры нормальных сил (рис.
2.3, г).
Вправо
будем откладывать положительные
значения, а влево – отрицательные значения
нормальных
сил.

Анализируя
построенную эпюру (N)
,
заметим, что внутренние силы не зависят
от размеров поперечного сечения, а
зависят только от приложенных внешних
сил. Поэтому длину бруса разбивают на
такое число участков, сколько
сил на его длине приложено. В данном
случае было два участка.

При
проверке правильности построения эпюры
следует обратить внимание
на то, что на эпюре внутренних сил в тех
сечениях, где были приложены
внешние силы, должны быть скачки, равные
приложенной внешней силе.

4.
Построим эпюру напряжений (σ).
Брус следует разбить на участки.
Поскольку
σ
= N/S,
то
участков на эпюре будет столько, сколько
раз меняется поперечное
сечение; при этом следует обращать
внимание, чтобы при постоянной
площади поперечного сечения нормальная
сила на эпюре N
оставалась
неизменной. С учетом этого на эпюре (σ)
будут три различных значения σ

(рис.
2.3, д):

σ₁
=
N₁/
S₁
= F/S;

σ₂
= N₂/S₂
= F/2S;

σ₃
= N₂/S₂
= -2F/2S
= –F/S.

5.Строим
эпюру перемещений (U).
Начинать следует от неподвижного
сечения,
т.е. от сечения О.
Выразим
перемещение сечения, находящегося от
неподвижного
на расстоянии z₂:

Если
0
≤ z₂
≤ l
, то для z₂
= l
перемещение

Для
l
≤ z
≤ 2l

Или

при z
= 2l

Для 2l
≤ z₁
≤ 3l

при z₁
= 3
l

Откладываем
вычисленные перемещения на эпюре (U)
(рис. 2.3, e).

Диаграмма
растяжения. Наиболее
наглядно особенности диаграммы
растяжения можно показать на примере
испытания образца из малоуглеродистой
стали (рис. 2.4). Диаграмма вычерчена
в координатах F,Δl.
На кривой можно выделить четыре зоны.

Зона ОА
носит название
зоны упругости.
Здесь материал
подчиняется закону Гука и

.

На рис. 2.4 этот
участок для большей наглядности показан
с отступлением от масштаба. Удлинения
на участке ОА
очень малы,
и прямая ОА,
будучи
вычерченной в масштабе, совпадала
бы в пределах ширины линии с осью ординат.
Значение силы, для которой справедлив
закон Гука, зависит от размеров образца
и физических свойств материала,
поэтому при дальнейшем рассмотрении
диаграммы растяжения ее перестраивают
в координатах σ
и ε

Зона АВ
называется
зоной общей
текучести, а
участок АВ
– площадкой
текучести. Здесь
происходит существенное изменение
длины образца без заметного увеличения
нагрузки. Не все металлы имеют площадку
текучести. Например, у алюминия,
отожженной меди, легированных сталей
площадка текучести не обнаруживается.

З
она
ВС называется
зоной
упрочнения. Здесь
удлинение образца

сопровождается
возрастанием на-грузки. В стадии
упрочнения на

образце намечается
место будущего разрыва и начинает
образовываться так называемая шейка
– местное
сужение образца. При дальнейшем
растяжении образца шейка быстро
прогрессирует. Начиная с точки С

удлинение
образца происходит с

уменьшением
силы, но среднее напряжение в поперечном
сечении шейки возрастает. Удлинение
образца носит в этом случае мест-ный
характер, по этому участок CD
называется
зоной местной
текучести
Рис.
2.4

Точка D
соответствует
разрушению образца.

Относительная
поперечная деформация.
При растяжении
(сжатии)

прямого бруса кроме продольной
деформации е происходит изменение
поперечных размеров бруса (рис.2.5). Ширина
бруса b
при
растяжении

уменьшается
на Δb.
Если Δb
отнести
к первоначальной ширине, то получим
выражение для определения относительной
поперечной деформации:

Отношение
относительной поперечной

деформации к
относительной продольной деформации
называют коэффициентом
Пуассона и
обозначают

:

Рис. 2.5.

Коэффициент
Пуассона, так же как и модуль упругости
Е, характеризует
физические свойства материала; его
значение колеблется для металлов в
пределах от 0,25 до 0,35. Некоторые значения
коэффициента и. приведены в табл. 2.1.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Привет! В этой статье поговорим о самом простом, но очень важном виде деформации – растяжении (сжатии). Обычно, с этого студенты и начинают изучать сопромат.

Здесь принято вводить основные понятия, которые используются на протяжении всего курса.

Растяжение (сжатие) – это вид деформации, при котором в поперечных сечениях растянутого (или сжатого) стержня возникают продольные силы (N).

Что такое продольная сила?

Соответственно, продольная сила – это внутренний силовой фактор, возникающий при деформации растяжения (сжатия).

В задачах на растяжение (сжатие) всё начинается с нахождения этих самых продольных сил. Зная, которые можно определить другие, очень важные характеристики: напряжения, перемещения и т. д.

Как определить продольную силу?

Продольные силы определяются методом сечений.

Расчетная схема стержня, работающего на растяжение (сжатие)

Когда стержень рассекается на две части, действие частей друг на друга заменяется продольными силами:

Мысленное рассечение стержня на две части с целью определения продольных сил

Затем, из уравнения равновесия, находятся их значения:

Отбрасывание одной из частей, и формирование расчетной схемы для составления уравнения равновесия

Для понимания, как распределены продольные силы по длине стержня, принято строить эпюру продольных сил. Подробный урок, по построению эпюры продольных сил можно найти, перейдя по указанной ссылке.

Что по поводу нормальных напряжений?

Нормальные напряжения также можно найти в любом сечении. Для этого нужно продольную силу в этом сечении разделить на площадь этого сечения:

Формула для определения нормальных напряжений

Так же, как и в случае с продольными силами, принято строить эпюру нормальных напряжений. Чтобы видеть наиболее опасные участки рассматриваемого стержня. Подробнее, про эпюры нормальных напряжений можно почитать в этой же статье.

Как найти перемещения?

В случае с растяжением (сжатием), стержни либо удлиняются, либо укорачиваются.

Схема, показывающая удлинение стержня с обозначениями

Например, для схемы, представленной выше, удлинение свободного торца можно посчитать по формуле:

где N – продольная сила в сечениях;

l – длина стержня до приложения внешней силы;

E – модуль упругости, материала из которого изготовлен стержень;

A – площадь поперечного сечения стержня.

Для перемещений тоже принято строить эпюры – эпюры осевых перемещений поперечных сечений. Также можешь найти подробности в ранее указанной статье.

Как насчет расчетов на прочность?

В этом разделе поговорим о расчетах на прочность при растяжении (сжатии), а также рассмотрим несколько примеров.

Условие прочности при растяжении (сжатии)

Условие прочности при растяжении (сжатии) выглядит следующим образом:

То есть рассчитываемый элемент можно считать прочным, если максимальное нормальное напряжение (σ_max) возникающее в элементе меньше, либо, по крайней мере, равно допустимому — [σ].

Нормальные напряжения (σ) в сечениях определяются по формуле:

Формула для определения нормальных напряжений при растяжении (сжатии)

где N – продольная сила в сечении;

A – площадь сечения.

Площадь простых сечений можно посчитать по этим формулам.

Допустимое напряжение

Как правило, в задачах, допустимое напряжение [σ] уже задано по условию. Для стали, по традиции, принимают [σ] = 160 МПа.

Если же [σ], по условию задачи не дано явно, то допустимое напряжение можно вычислить по формуле:

где σ_пред – предельное напряжение;

n – коэффициент запаса прочности.

Очевидно, за предельное напряжение для разных материалов принимают различное значение. Для пластичных материалов, например, для малоуглеродистой стали (Ст2, Ст3) принимают предел текучести, а для хрупких материалов (бетон, чугун) берут в качестве предельного напряжения – предел прочности (временное сопротивление). Эти характеристики получают при испытании образцов на растяжение (сжатие), с помощью специальных машин, которые фиксируют характеристики материалов в виде диаграмм.

Коэффициент запаса прочности

Коэффициент запаса прочности (n) выбирается конструктором исходя из своего личного опыта, назначения или сферы применения проектируемой детали. Обычно коэффициент запаса прочности варьируется от 2 до 6.