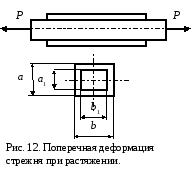
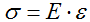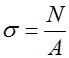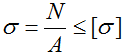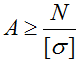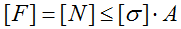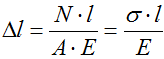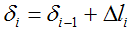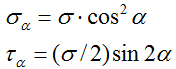Подборка формул для расчета элементов и конструкций на растяжение-сжатие и решения задач сопротивления материалов по расчету нормальных напряжений, деформаций и перемещения сечений стержней при продольном нагружении.
Обозначения в формулах:
σ — нормальные напряжения,
N – внутренняя продольная сила,
A – площадь поперечного сечения,
[σ] – допустимые напряжения,
E – модуль продольной упругости,
ε — относительные деформации.
Закон Гука:
Формула для расчета напряжений в поперечном сечении стержня
Условие прочности (проверочный расчет) при растяжении-сжатии
Расчет минимальной площади поперечного сечения бруса
Расчет допустимой величины внешней растягивающей/сжимающей силы (определение грузоподъемности)
Формула для расчета абсолютных деформаций
Расчет перемещения сечений
Здесь: δi — перемещение рассматриваемого сечения,
δi-1 — перемещение предыдущего сечения,
Δli — деформация участка между указанными сечениями.
Напряжения в наклонных сечениях
Здесь α — угол отклонения сечения от поперечного.
Другие формулы >
Примеры решения задач >
Краткая теория >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
2.1 Внутренние усилия и напряжения при растяжении (сжатии)
Р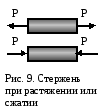
(сжатие) –
простой вид сопротивления, при котором
стержень нагружен силами, параллельными
продольной оси стержня и приложенными
в центр тяжести его сечения.
Рассмотрим
стержень, упруго растянутый центрально
приложенными сосредоточенными силами
P.
Прежде
чем перейти к исследованию внутренних
усилий и напряжений, возникающих в
растянутом стержне, рассмотрим некоторые
гипотезы, связанные с характером
деформирования такого стержня и имеющие
в сопротивлении материалов исключительно
важное значение.
Принцип
Сен-Венана:
в сечениях,
достаточно удаленных от мест приложения
сил, распределение напряжений и деформаций
мало зависит от способа приложения
нагрузок.
Принцип
Сен-Венана дает возможность вести расчет
без учета местных (локальных) деформаций,
возникающих вблизи точек приложения
внешних сил и отличающихся от деформаций
основного объема материала, что в
большинстве случаев упрощает решение
задачи.
Г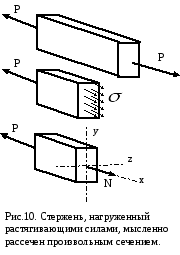
плоских сече-ний (гипотеза Я.Бернулли):
поперечные
сечения стержня плоские и перпендикулярные
его оси до деформации остаются плоскими
и перпендикулярными оси, и после
деформации.
Мысленно
рассекая стер-жень, определим внутренние
силы в растянутом стержне:
а)
стержень, нагруженный растя-гивающими
силами P
и находя-щийся в равновесии, рассекаем
произвольным сечением;
б)
отбрасываем одну из частей стержня, а
ее действие на дру-гую часть компенсируем
вну-тренними усилиями интенсив-ностью;
в)
осевое внутреннее усилие N, возникающее
в сечении стержня, определим, составляя
уравнения равновесия для отсеченной
части:
.
(2.1)
Проецируя
внешнюю силу P,
действующую на отсеченную часть стержня,
на другие оси (z
и y), а также составляя уравнения моментов
относительно координатных осей, легко
убедится, что осевое усилие N является
единственным внутренним усилием,
возникающим в сечении стержня (остальные
тождественно равны нулю).
Таким
образом, при растяжении (сжатии) из шести
внутренних усилий в сечении стержня
возникает только одно — продольная
сила N.
Нормальные
напряжения
,
возникающие в сечении стержня, связаны
с осевым усилием N следующим образом:
,
или
. (2.2)
Учитывая,
что в соответствии с гипотезой Бернулли
напряжения равномерно распределены по
поперечному сечению (т.е.
=const),
можно записать:
.
(2.3)
Таким
образом, нормальные напряжения при
растяжении (сжатии) определяются как
. (2.4)
2.2 Перемещения и деформации при растяжении (сжатии)
Р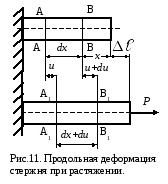
стержень, находящийся под действием
растягивающей нагрузки. Выделим (до
деформации) двумя произвольными сечениями
А-А и В-В бесконечно малый участок длинойdx
на расстоянии x
от свободного конца. Под действием
внешней силы P
сечение А-А переместиться в положение
А1-А1
на расстояние u,
а сечение В-В – в положение В1-В1
на расстояние u+du
(du
– бесконечно малая величина) Следовательно,
абсолютное удлинение отрезка dx
равно разности его размеров до и после
деформации Δdx
= du.
Относительная
продольная деформация точек сечения
А-А стержня при растяжении
(2.5)
Для
линейно-упругого матери-ала связь между
нормальными напряжениями и относительной
деформацией при растяжении определяется
законом Гука:
,
(2.6)
или,
учитывая, что
,
,
(2.7)
где
Е – модуль нормальной упругости (модуль
Юнга), постоянный коэффициент, который
является константой материала (например,
для стали Е=2∙1011
Па, для меди Е=1,2∙1011
Па, для титана Е=1,2∙1011
Па).
Исходя
из этих формул, можно записать выражение
для перемещений точек растягиваемого
стержня в рассматриваемом сечении
,
,
(2.8)
Тогда
полное удлинение стержня при растяжении
,
равное перемещению точек правого
крайнего сечения, относительно левого
крайнего:
(2.9)
При
постоянстве величин N,
F,
Е вдоль оси
стержня, абсолютное удлинение можно
найти так:
.
(2.10)
При
растяжении стержень деформируется не
только в продольном направлении, но и
в поперечном.
Абсолютная
поперечная деформация стержня
опреде-ляется как разность его поперечных
размеров до и после деформации:
;
.
Относительная
поперечная деформация
стержня определяется отношением
абсолютной поперечной деформации к
соответствующему первоначальному
размеру.
Относительная
поперечная деформация при растяжении
(сжатии) для изотропных материалов во
всех направлениях одинакова:
(2.11)
.
Между
относительной поперечной и продольной
деформациями прирастяжении (сжатии) в
пределах применимости закона Гука
существует постоянное соотношение,
которое называется коэффициентом
поперечных деформаций (коэффициентом
Пуассона µ).
Коэффициент
Пуассона равен абсолютной величине
отношения поперечной деформации к
продольной
.
(2.12)
Коэффициент
Пуассона – безразмерная величина.
Так
как продольная и поперечная деформация
для конструкционных материалов имеют
противоположные знаки, можем записать
(2.13)
или,
учитывая, что, согласно закону Гука,
запишем
(2.14)
Коэффициент
Пуассона µ
также как и модуль Юнга Е
характеризует упругие свойства материала.
Для изотропных материалов коэффициент
Пуассона находится в пределах от 0 до
0,5 (сталь
;
каучук).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Сила упругости широко используется в технике. Эта сила возникает в упругих телах при их деформации. Деформация – это изменение формы тела, под действием приложенных сил.
Виды деформации
Деформация – это изменение формы, или размеров тела.
Есть несколько видов деформации:
- сдвиг;
- кручение;
- изгиб;
- сжатие/растяжение;
Деформация сдвига возникает, когда одни части тела сдвигаются относительно других его частей. Если подействовать на верхнюю часть картонного ящика, наполненного различными предметами, горизонтальной силой, то вызовем сдвиг верхней части ящика относительно его нижней части.
Сжатие или растяжение легко представить на примере прямоугольного куска тонкой резины. Такая деформация используется, к примеру, в резинках для одежды.
Примеры изгиба и кручения показаны на рисунке 1. Пластиковая линейка, деформированная изгибом, представлена на рис. 1а, а на рисунке 1б – эта же линейка, деформируемая кручением.
Рис. 1. пластиковая линейка, деформированная изгибом – а) и кручением – б)
В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.
Растяжение пружины
Рассмотрим подробнее деформацию растяжения на примере пружины.
Давайте прикрепим пружину к некоторой поверхности (рис. 2). На рисунке слева указана начальная длина (L_{0}) пружины.
Рис. 2. Сравнивая длину свободной пружины с длиной нагруженной, можно найти ее удлинение
Подвесим теперь к пружине груз. Пружина будет иметь длину (L), указанную на рисунке справа.
Сравним длину нагруженной пружины с длиной свободно висящей пружины.
[ large L_{0} + Delta L = L ]
Найдем разницу (разность) между длинами свободно висящей пружины и пружины с грузом. Вычтем для этого из обеих частей этого уравнения величину (L_{0}).
[ large boxed{ Delta L = L — L_{0} }]
( L_{0} left(text{м} right) ) – начальная длина пружины;
( L left(text{м} right) ) – конечная длина растянутой пружины;
( Delta L left(text{м} right) ) – кусочек длины, на который растянули пружину;
Величину ( Delta L ) называют удлинением пружины.
Иногда рассчитывают относительное удлинение. Это относительное удлинение часто выражают десятичной дробью. Или дробью, в знаменателе которой находится число 100 — такую дробь называют процентом.
Примечание: Отношение – это дробь. Относительное – значит, дробное.
[ large boxed{ frac{Delta L }{ L_{0}} = frac{ L — L_{0}}{L_{0} } = varepsilon } ]
( varepsilon ) – это отношение (доля) растяжения пружины к ее начальной длине. Измеряют в процентах и называют относительным удлинением.
Расчет силы упругости
Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.
Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.
Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.
Разноцветная пластмассовая пружина-игрушка растяжению сопротивляется слабо
Закон Гука
Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал ( F_{text{упр}} ) силой упругости.
[ large boxed{ F_{text{упр}} = k cdot Delta L }]
Эту формулу назвали законом упругости Гука.
( F_{text{упр}} left( H right) ) – сила упругости;
( Delta L left(text{м} right) ) – удлинение пружины;
( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости).
Какие деформации называют малыми
Закон Гука применяют для малых удлинений (деформаций).
Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.
Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.
Как рассчитать коэффициент жесткости
Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.
Рис. 4. Вес подвешенного на пружине груза уравновешивается силой упругости
Так как силы взаимно компенсируются, в правой части уравнения находится ноль.
[ large F_{text{упр}} — m cdot g = 0 ]
Подставим в это уравнение выражение для силы упругости
[ large k cdot Delta L — m cdot g = 0 ]
Прибавим к обеим частям вес груза и разделим на измеренное изменение длины (Delta L ) пружины. Получим выражение для коэффициента жесткости:
[ large boxed{ k = frac{ m cdot g }{Delta L} }]
(g) – ускорение свободного падения, оно связано с силой тяжести.
Соединяем две одинаковые пружины
В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.
Параллельное соединение пружин
На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину (Delta L). Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.
Рис. 5. Две пружины, соединенные параллельно, деформируются меньше одной такой пружины
Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом (mg).
Одна пружина:
[ large k_{1} cdot Delta L = m cdot g ]
Две параллельные пружины:
[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= m cdot g ]
Так как правые части уравнений совпадают, левые части тоже будут равны:
[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= k_{1} cdot Delta L ]
Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:
[ large k_{text{параллел}} cdot frac{1}{2}= k_{1} ]
Умножим обе части полученного уравнения на число 2:
[ large boxed{ k_{text{параллел}} = 2k_{1} } ]
Коэффициент жесткости (k_{text{параллел}}) двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной
Последовательное соединение пружин
Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину (Delta L). Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.
Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.
На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину (Delta L).
Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений
Рис. 6. Система, состоящая из двух одинаковых пружин, соединенных последовательно, деформируются больше одной пружины
Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом (mg).
Одна пружина:
[ large k_{1} cdot Delta L = m cdot g ]
Две последовательные пружины:
[ large k_{text{послед}} cdot Delta L cdot 2 = m cdot g ]
Так как правые части уравнений совпадают, левые части тоже будут равны:
[ large k_{text{послед}} cdot Delta L cdot 2 = k_{1} cdot Delta L ]
Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:
[ large k_{text{послед}} cdot 2 = k_{1} ]
Разделим обе части полученного уравнения на число 2:
[ large boxed{ k_{text{послед}} = frac{k_{1}}{2} } ]
Коэффициент жесткости (k_{text{послед}}) двух пружин, соединенных последовательно, уменьшится вдвое, в сравнении с одной такой пружиной
Потенциальная энергия сжатой или растянутой пружины
Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину (Delta L ) обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу, например, по перемещению груза. В таких случаях физики говорят, что пружина обладает потенциальной энергией.
Рис. 7. Деформированная — сжатая или растянутая пружина обладает потенциальной энергией
Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).
Чем больше жесткость (упругость) пружины, тем больше ее потенциальная энергия. Увеличив удлинение пружины получим повышение ее потенциальной энергии по квадратичному закону:
[ large boxed{ E_{p} = frac{k}{2} cdot left( Delta L right)^{2} }]
( E_{p} left( text{Дж} right)) – потенциальная энергия сжатой или растянутой пружины;
( Delta L left(text{м} right) ) – удлинение пружины;
( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости) пружины.
Выводы
- Упругие тела – такие, которые сопротивляются деформации;
- Во время деформации в упругих телах возникает сила, она препятствует деформации, ее называют силой упругости;
- Деформация – изменение формы, или размеров тела;
- Есть несколько видов деформации: изгиб, кручение, сдвиг, растяжение/сжатие;
- Удлинение пружины – это разность ее конечной и начальной длин;
- Сжатая или растянутая пружина обладает потенциальной энергией (вообще, любое упруго деформированное тело обладает потенциальной энергией);
- Система, состоящая из нескольких одинаковых пружин, будет иметь коэффициент жесткости, отличный от жесткости единственной пружины;
- Если пружины соединяют параллельно – коэффициент жесткости системы увеличивается;
- А если соединить пружины последовательно – коэффициент жесткости системы уменьшится.
Привет! В этом уроке начнём знакомиться с таким видом деформации, как растяжение (сжатие). Обычно, с этой темы и начинают изучать сопротивление материалов — объясняются основные понятия, которые дальше используются на протяжении всего обучения.
Задание, которое будем рассматривать в этой статье, как правило, дается студентам в первую очередь в качестве домашней работы. После изучения материалов этого урока ты научишься строить следующие эпюры: продольных сил, нормальных напряжений, а также осевых перемещений поперечных сечений. Не пугайся мудрёных названий, на самом деле, все эти эпюры строятся очень просто!
Что же давай приступим к изучению!
Построение эпюры продольных сил
В качестве примера возьмём простенькую расчётную схему стержня (также часто ступенчатый стержень, который работает на растяжение или сжатие, называют брусом). Загрузим наш стержень сосредоточенными силами, вот так:

Теперь наша первостепенная задача – построить эпюру продольных сил. И давай сразу будем разбираться в терминологии.
Что такое эпюра?
Эпюра – это график, который принято строить для визуализации распределения какой-либо величины. В нашем случае, продольной силы.
Построив такой график, мы можем увидеть, где определённая величина достигает максимальных или минимальных значений, что может быть полезно при проведении прочностных расчётов и других. Кроме того, эпюры могут служить вспомогательными инструментами для построения других эпюр, о чём мы будем говорить далее.
Что такое продольная сила?
Продольная сила – это внутренняя сила, которая возникает в сечениях стержня, работающего на растяжение или сжатие под действием внешней нагрузки.
Расчёт эпюры продольных сил
Чтобы построить эпюру продольных сил, нужно разбить брус на несколько участков, где эпюра будет иметь постоянное значение. Конкретно, для этого стержня, границами участков служат те точки, где прикладываются сосредоточенные силы.
То есть для нашего примера, нужно рассмотреть всего 2 участка:

Важно! Эпюра продольных сил, никак не зависит от формы бруса, в отличие от других эпюр, которые будем дальше рассчитывать.
Правило знаков для продольных сил
Правило знаков для продольных сил следующее:
- если внешняя сила (F) растягивает брус, то продольная сила (N) в сечениях будет положительная;
- если внешняя сила (F) сжимает брус, то продольная сила (N) в сечениях будет отрицательная.

Расчёт продольных сил на участках
На первом участке сила F1 растягивает брус на величину 5 кН, поэтому на этом участке, продольная сила будет положительной и равной:
Откладываем это значение на графике — эпюре. Эпюры, принято заштриховывать перпендикулярно к нулевой линии, а также указывать знак продольной силы:

На втором же участке, помимо силы F1, также действует сила F2, которая сжимает брус, поэтому в уравнении ее нужно учесть со знаком «минус»:
Откладываем полученное значение на эпюре:

Расчёт реакции в жёсткой заделке
Прежде всего, следует разобраться с тем, что вообще такое реакция. Всё дело в том, что помимо внутренних усилий, возникающих внутри нагруженного элемента конструкции, в том месте, где закреплён этот элемент, также возникают некоторые силы (сила), которые являются реакцией на внешнюю нагрузку и удерживающие эту конструкцию в состоянии статического равновесия.
Например, стул на котором ты сейчас сидишь и давишь на него своим весом, сопротивляется, чтобы удерживать тебя в состоянии равновесия. Если переводить на язык сопромата, твой вес в этом случае это внешняя сила, а сила с которой стул реагирует на твой вес – это реакция опоры, равная по модулю этой силе, но противоположно направленная.
Так и в нашей конструкции, в жёсткой заделке, также возникает реакция! Осталось только научиться — определять эту силу. Так как она должна компенсировать всю нагрузку, которая приложена к стержню, условие равновесия для нашей схемы можно записать так:
То есть, так как система находится в состоянии равновесия, то сумма всех сил, действующих на конструкцию, будет равна нулю.
Из этого условия равновесия и найдём искомую реакцию. Приложим некоторую силу R в месте, где закреплён наш стержень, при этом направить её можно в любую сторону, хоть влево, хоть вправо, главное, чтобы она была направлена горизонтально, так как у нас вся нагрузка, направлена так, то и реакция в заделке будет возникать исключительно — горизонтальная:

Чтобы составить уравнение равновесия, введём продольную ось – x, относительно неё будем составлять это уравнение, при этом силы, которые будут совпадать с положительным направлением оси x, в уравнении будем учитывать с «плюсом», а противоположно направленные с «минусом»:

Находим из этого уравнения реакцию в заделке:
А теперь, давай обсудим, что можем делать с этим теперь. В нашей конкретной задаче реакция может помочь проверить эпюру продольных сил. Если в первом уроке, считали стержень, строго справа налево, то теперь, зная численное значение реакции, можно рассчитать стержень и слева направо. Или как минимум увидеть, что левый участок эпюры, был построен верно.
Да, можно было вполне обойтись, без расчёта этой реакции конкретно в этом случае. Но, чаще всего, решение задач по сопромату начинается как раз с определения реакций, потому что без этого в большинстве случаев, невозможно определить внутренние усилия, а тем самым произвести какие-либо дальнейшие расчёты. Но с этим мы ещё многократно будем сталкиваться в следующих уроках, особенно в задачах на изгиб.
Построение эпюры нормальных напряжений
В отличие от продольных сил, нормальные напряжения уже зависят от формы бруса, а если точнее, то от площади его поперечных сечений.
Формула для определения нормальных напряжений выглядит так:

Таким образом, чтобы найти нормальное напряжение в любом сечении бруса, нужно: продольную силу в этом сечении разделить на площадь сечения.
Нормальные напряжения, как и продольные силы, изменяются по одному закону в пределах участков. Однако, так как форма бруса сказывается на распределении нормальных напряжений, здесь границами участков также служат места изменения геометрии бруса. Таким образом, для нашей расчетной схемы, нужно рассмотреть три участка и вычислить напряжения, соответственно, 3 раза:

Будем считать, что по условию задачи нам известны все параметры бруса, включая площади поперечных сечений: на первом участке площадь поперечного сечения A1=2 см2, а на втором и третьем A2 = A3 = 4 см2.

Вычисляем напряжения на каждом участке:

По полученным значениям строим эпюру нормальных напряжений:

По полученной эпюре нормальных напряжений, можно определить те поперечные сечения, в которых напряжения будут максимальными (все сечения на участке 1), что полезно при проведении прочностного расчёта.
Построение эпюры осевых перемещений поперечных сечений
Под действием внешней нагрузки поперечные сечения бруса перемещаются вдоль продольной оси. Под нагрузкой брус может как удлиниться, так и укоротиться. И в этом разделе будем учиться определять эти перемещения.
Для начала подготовимся к расчету и расставим точки в характерных сечениях. Чтобы потом к ним привязываться по ходу решения:

Если для первых двух эпюр, расчет начинался справа налево, от свободного конца. То здесь нам нужно начать считать с закрепленного конца, с жесткой заделки и так как сечение A, закреплено жестко, то никакие перемещения этого сечения невозможны, поэтому сразу можем записать:
Эпюра перемещений так же, как и остальные эпюры, меняется по одному закону, в пределах участков. Поэтому, чтобы построить эпюру, достаточно определить эти перемещения в характерных точках.
Перемещение точки B будет складываться из перемещения предыдущего расчетного сечения:
А также удлинения (или укорочения) участка между расчетными сечениями:
В свою очередь, удлинение (или укорочение) любого участка, можно определить по следующей формуле:

Поэтому формулу, для нахождения перемещения сечения B, можно записать и в другом виде:

Подставив все численные значения, найдем искомое перемещение:

Откладываем полученное значение на эпюре:

Также важно отметить, что при вычислении удлинения или укорочения участка (Δl), фактически площадь эпюры продольных сил (ω) делится на жесткость при растяжении или сжатии (EA).


Это свойство нам еще пригодится, когда будем рассматривать более сложную задачу.
Для точек C и D перемещения находятся аналогичным способом, так же как и для точки B, поэтому подробно комментировать не буду, приведу решение.
Точка C

Точка D

Откладываем полученные значения на эпюре:

По полученной эпюре, можно увидеть — в какую сторону и насколько переместится любое поперечное сечение стержня. Наиболее интересной характеристикой здесь является перемещение сечения D, то есть перемещение свободного конца бруса или фактическое удлинение. Как видим, сечение D переместится вправо на величину WD (т. к. значение WD — положительное). То есть, под действием всей нагрузки брус удлинится на 0.575 мм.
Учёт распределённой нагрузки
А теперь предлагаю рассмотреть немного измененную задачу. Приложим к нашему брусу дополнительно распределенную нагрузку q с интенсивностью равной 2 кН/м. После чего рассчитаем и построим все те же эпюры: продольных сил, нормальных напряжений и перемещений.

Чтобы учесть распределенную нагрузку, необходимо интенсивность нагрузки (q) умножить на длину участка, на котором действует нагрузка. В чистом виде, только от распределенной нагрузки, эпюра продольных сил будет треугольная.

Расчет продольных сил
На первом участке, сила по-прежнему растягивает стержень, записываем ее в уравнение с «плюсом», а распределенная нагрузка сжимает, соответственно, ее учитываем с «минусом»:
Найдем значения продольной силы на границах первого участка:

Откладываем рассчитанные значения:

На втором участке, распределенная нагрузка будет действовать точно так же, как и сосредоточенная сила:
Рассчитываем продольную силу на третьем участке:
Строим окончательную эпюру продольных сил:

Расчет нормальных напряжений
Нормальные напряжения рассчитываются точно так же, как и для первой задачи, единственное отличие только в том, что на первом участке необходимо рассчитать напряжения два раза — на границах участка:

По полученным значениям строим эпюру нормальных напряжений:

Расчет перемещений
Для точек A, B и С перемещения рассчитываются аналогично, как в первой задаче:


Строим эпюру перемещений на втором и третьем участке:

Чтобы рассчитать удлинение на первом участке, нужно вычислить площадь эпюры продольных сил на этом участке и разделить на жесткость (EA):


Так как на этом участке, эпюра состоит из двух одинаковых прямоугольных треугольников, но по разные стороны от нулевой линии, с учетом знаков, ожидаемо, получим, что перемещение точки D, будет равно перемещению точки C.



Однако, необходимо учесть еще одну особенность. На участках, где действуют распределенные нагрузки, эпюры перемещений изменяются не по линейному закону, а по квадратичному.
То есть на участке с распределенной нагрузкой, эпюра перемещений всегда будет иметь либо выпуклость, либо вогнутость:

Чтобы понять, как же будет выглядеть эпюра перемещений, на участке с распределённой нагрузкой, нужно проанализировать эпюру продольных сил.
Как видим, начиная от точки C и до пересечения нулевой линии, эпюра продольных сил – отрицательна, а это значит, что эпюра перемещений, на этом отрезке, также должна убывать, как показано зелёной пунктирной линией. Поэтому изображаем эпюру перемещений следующим образом:

Но чтобы окончательно убедиться в верности наших рассуждений, можно также определить экстремум на эпюре перемещений (там, где эпюра достигает своего максимального значения). Или в той точке, где эпюра продольных сил пересекает нулевую линию:


Отмечаем найденное значение на эпюре перемещений:

§1. Продольные силы в поперечных сечениях
§1. Продольные силы в поперечных сечениях
Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только продольные силы N, а прочие силовые факторы (поперечные силы, крутящий и изгибающий моменты) равны нулю.
Это самый простой и часто встречающийся вид деформации. Обычно он наблюдается когда внешняя нагрузка действует вдоль продольной оси стержня. Продольной осью стержня называется линия, проходящая через центры тяжести поперечных сечений.
Обычным является растяжение стержня силами, приложенными к его концам. Передача усилий к стержню может быть осуществлена различными способами, как это показано на рис. 1.
Рис. 1. Растяжение стержня
Во всех случаях, однако, система внешних сил образует равнодействующую F, направленную вдоль оси стержня. Поэтому независимо от условий крепления растянутого стержня, расчетная схема в рассматриваемых случаях (рис. 1, а, б) оказывается единой (рис. 1, в) согласно принципу Сен – Венана.
Если воспользоваться методом сечений (рис. 2), то становится очевидным, что во всех поперечных сечениях стержня возникают нормальные силы Nz, равные силе F (рис. 2, б).
Сжатие отличается от растяжения, формально говоря, только знаком силы Nz. При растяжении нормальная сила Nz направлена от сечения (рис. 2, б), а при сжатии – к сечению.
Рис. 2. Нормальная сила N
Растягивающие продольные силы принято считать положительными (рис. 3, а), а сжимающие – отрицательными (рис. 3, б).
Рис. 3. Знак продольной силы N
При расчете стержней, испытывающий деформацию растяжения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от Nz), возникающих в стержне, и нахождение линейных перемещений в зависимости от внешней нагрузки.
Продольные силы (Nz), возникающие в поперечных сечениях стержня, определяются по внешней нагрузке с помощью метода сечений.
График, показывающий изменение продольных сил по длине оси стержня, называется эпюрой продольных сил (эп. Nz). Он дает наглядное представление о законе изменения продольной силы.
Осью абсцисс служит ось стержня. Каждая ордината графика – продольная сила (в масштабе сил) в данном сечении стержня.
Эпюра позволяет определить, в каком сечении действует максимальное внутреннее усилие (например, найти Nmax при растяжении-сжатии). Сечение, где действует максимальное усилие будем называть опасным.
Перед построением эпюр необходимо освободить брус, в котором будем строить эпюры от опорных связей (выделить объект равновесия) и приложить к нему все действующие внешние силы (активные и реактивные). Затем необходимо установить границы участков, в пределах которых закон изменения внутренних сил постоянный. Границами таких участков являются сечения, где приложены сосредоточенные силы или начинается и кончается распределенная нагрузка, а также сечения, где имеется перелом стержня.
Применяя метод сечений и учитывая правила знаков изложенные выше, получаем уравнения изменения внутренних сил в пределах длины каждого участка бруса. Затем, используя, полученные зависимости строим графики (эпюры) этих усилий. Ординаты эпюр в определенном масштабе откладываем от базисной линии, которую проводим параллельно оси бруса.
На основании метода сечений продольная сила в произвольном поперечном сечении стержня численно равна алгебраической сумме проекций внешних сил, приложенных к стержню по одну сторону от рассматриваемого сечения, на его продольную ось.
Причем проекция внешней силы берется со знаком плюс, если сила растягивает часть стержня от точки ее приложения до рассматриваемого сечения и, наоборот, со знаком минус – если сжимает.
§2. Напряжение в поперечных сечениях стержня
При растяжении или сжатии осевыми силами стержней из однородного материала поперечные сечения, достаточно удаленные от точек приложения внешних сил ,остаются плоскими и перемещаются поступательно в направлении деформации. Это положение называют – гипотезой плоских сечений. На основании указанного можно заключить, что все точки какого-либо поперечного сечения стержня находятся в одинаковых условиях и, следовательно, напряжения распределяются по сечению равномерно. Эти напряжения перпендикулярны поперечному сечению, а значит, являются нормальными напряжениями. Их значения найдем, разделив продольную силу N на площадь А: σ=N/A
Продольная сила N с помощью метода сечений всегда может быть выражена через внешние силы. В формулe следует подставлять алгебраическое значение N т.е со знаком плюс в случае растяжения и со знаком минус в случае сжатия
§3. Расчеты на прочность и жесткость при растяжении-сжатии
Прочность стержня при осевом растяжении и сжатии обеспечена, если для каждого его поперечного сечения наибольшее расчетное (рабочее) напряжение σ не превосходит допускаемого [σ] : σ=N/A≤ [σ],
где N – абсолютное продольной силы в сечении;
А – площадь поперечного сечения;
[σ] – допускаемое напряжение пр растяжении или сжатии для материала стержня.
Данное выражение определяет условие прочности при растяжении или сжатии.
С помощью этой формулы решается три вида зада (выполняется три вида расчета):
1. Проверка прочности (проверочный расчет). При заданных продольной силы N и площади поперечного сечения А определяют рабочее (расчетное) напряжение и сравнивают его с допускаемым [σ].
Превышение рабочего (расчетного) напряжения не должно быть больше 5% , иначе прочность рассчитываемой детали считается недостаточной.
В случаях, когда рабочее напряжения значительно ниже допускаемых σ<<[σ], получаются неэкономичные конструкции чрезмерным необоснованным расходом материала. Такие решения являются нерациональными. Следует стремится к максимальному использованию прочности материала и снижения материалоемкости конструкций.
2. Подбор сечения (проектный расчет). Исходя из условия прочности можно определить необходимые размеры сечения, зная продольную силу N и допускаемое напряжение [σ]:
A≥N/[σ]
3. Определение допускаемой продольной силы. Допускаемое значение продольной силы в поперечном сечении стержня можно найти по формуле: [N]≤ [σ]·A
Значения допускаемых напряжение для некоторых материалов приведены в табл. 1.
Допускаемые напряжения назначаются на основе результатов механических испытаний образцов соответствующих материалов.
§4. Деформации и перемещения. Закон Гука
Рассмотрим однородный стержень с одним концом, жестко заделанным, и другим – свободным, к которому приложена центральная продольная сила Р (рис. 4). До нагружения стержня его длина равнялась l – после нагружения она стала равной
(рис. 4). Величину называют абсолютной продольной деформацией (абсолютным удлинением) стержня. В большинстве случаев оно мало по сравнению с его первоначальной длиной l (∆l<<l).
Рис. 4. Абсолютное удлинение стержня
Если в нагруженном стержне напряженное состояние является однородным, т.е. все участки стержня находятся в одинаковых условиях, деформация
остается одной и той же по длине стержня и равной ε = Δl/l
Величина ε называется относительной продольной деформацией.
В пределах малых деформаций при простом растяжении или сжатии закон Гука записывается в следующем виде (нормальные напряжения в поперечном сечении прямо пропорциональны относительной линейной деформации
): σ=Eε
Величина Е представляет собой коэффициент пропорциональности, называемый модулем упругости материала первого рода (модуль продольной упругости). Его величина постоянна для каждого материала. Он характеризует жесткость материала, т.е. способность сопротивляться деформированию под действием внешней нагрузки. Так как величина ε безразмерная, то E – измеряется в тех же единицах измерения то и напряжение, т. е. в Паскалях (Па). Значения модуля упругости E для некоторых конструкционных материалов приведены в табл. 2.
Δl=Nl/EA
Выведенное соотношение показывает, что удлинение (укорочение) при растяжении (сжатии) зависит от величины продольной силы N, поперечного сечения А стержня, его длины l и модуля продольной упругости Е. Произведение ЕА называется жесткостью сечения стержня при растяжении (сжатии).
При растяжении и сжатии изменяются и поперечные размеры стержня. Поперечный размер, первоначально равный a , уменьшается до a1. Изменение поперечно размера Δ a= a- a1, а поперечная деформация равна ε┴= Δ a/ a.
Экспериментально установлено что отношение поперечной деформации к продольной при упругом растяжении или сжатии есть величина постоянная и обозначается µ: µ= ε┴/ ε
Следует учитывать, что продольные и поперечные деформации всегда противоположны по знаку. Иными словами, при растяжении, когда продольный размер стержня увеличивается, его поперечный размер уменьшается, и, наоборот , при сжатии продольный размер уменьшается, а поперечный –увеличивается .
Величина µ называется коэффициентом поперечной деформации, или коэффициентом Пуассона. Коэффициент поперечной деформации для некоторых материалов имеет следующие значения:
сталь ….024-032,
медь….031-035,
бронза..032-035,
резина , каучук…047.