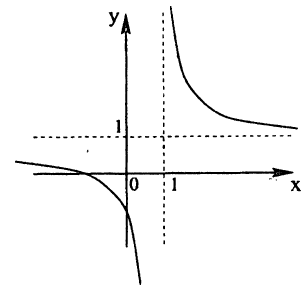
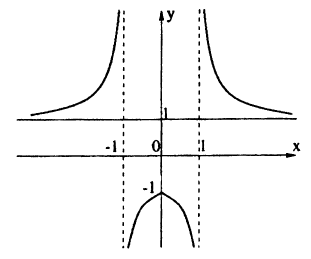
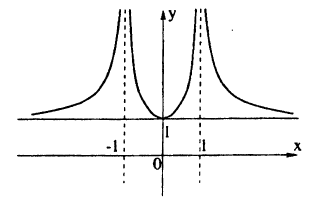
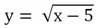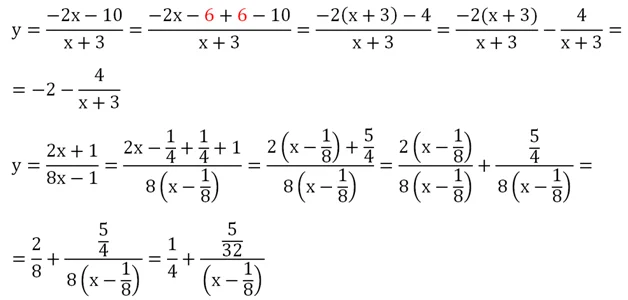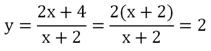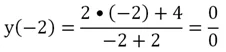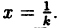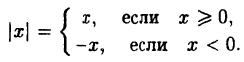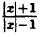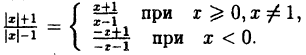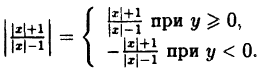Растяжение и сжатие графиков функций
- Список функций, изученных в 7 и 8 классе
- Растяжение и сжатие графика по оси OX
- Растяжение и сжатие графика по оси OY
- Примеры
Список функций, изученных в 7 и 8 классе
|
Функция |
Формула |
График |
Раздел справочника |
|
Прямая пропорциональность |
y = kx |
Прямая |
7 кл., §37 |
|
Линейная функция |
y = kx+b |
Прямая |
7 кл., §38-39 |
|
Обратная пропорциональность |
$ y = frac{k}{x} $ |
Гипербола |
8 кл., §6 |
|
Квадрат числа |
$ y=x^2$ |
Парабола |
8 кл., §18 |
|
Квадратный трёхчлен |
$ y = ax^2+bc+c$ |
Парабола |
8 кл., §28-29 |
|
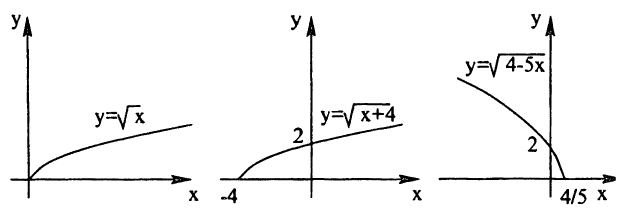
Квадратный корень |
$ y = sqrt{x}$ |
Парабола |
8 кл., §22 |
Растяжение и сжатие графика по оси OX
Сравним графики пар функций, которые в общем виде можно записать так:
$$ y_1 = f(x), y_2 = f(px) $$
где $p gt 1$, произвольный положительный множитель.
Пусть p = 2.
|
Парабола: $y_1 = f(x) = x^2$ $ y_2 = f(2x) = (2x)^2 = 4x^2 $ $y_2 = y_1 при x_2 = frac{1}{2} x_1$ График сжимается в 2 раза по оси OX |
 |
|
Гипербола: $ y_1 = f(x) = frac{4}{x}$ $y_2 = f(2x) = frac{4}{(2x)} = frac{2}{x}$ $ y_2 = y_1 при x_2 = frac{1}{2} x_1 $ График сжимается в 2 раза по оси OX |
|
|
Квадратный корень: $y_1 = f(x) = sqrt{x}$ $y_2 = f(2x) = sqrt{2x}$ $y_2=y_1 при x_2 = frac{1}{2} x_1$ График сжимается в 2 раза по оси OX |
|
Теперь сравним пары функций с делением на p:
$$ y_1 = f(x), quad y_2 = f left( frac{x}{p} right), quad p gt 1 $$
Пусть p = 2
|
Парабола: $y_1 = f(x) = x^2$ $ y_2 = f left(frac{x}{2}right) = left(frac{x}{2}right)^2 = frac{x^2}{4} $ $y_2 = y_1 при x_2 = 2x_1$ График растягивается в 2 раза по оси OX |
 |
|
Гипербола: $ y_1 = f(x) = frac{4}{x}$ $y_2 = f left(frac{x}{2}right) = frac{4}{x/2} = frac{8}{x}$ $ y_2 = y_1 при x_2 = 2x_1$ График растягивается в 2 раза по оси OX |
|
|
Квадратный корень: $y_1 = f(x) = sqrt{x}$ $y_2 = f left(frac{x}{2}right) = sqrt{frac{x}{2}}$ $y_2=y_1 при x_2 = 2x_1$ График растягивается в 2 раза по оси OX |
|
При сравнении графиков двух функций
$$ y_1 = f(x), quad y_2 = f(px), quad p gt 1 $$
график второй функции сжимается в p раз по оси OX по сравнению с графиком первой функции.
При сравнении графиков двух функций
$$ y_1 = f(x), quad y_2 = f Biggl(frac{x}{p}Biggr), quad p gt 1 $$
график второй функции растягивается в p раз по оси OX по сравнению с графиком первой функции.
Заметим, что данные утверждения справедливы не только для рассмотренных функций, но и для любых других (синусов, косинусов, логарифмов и т.п.)
Растяжение и сжатие графика по оси OY
Сравним графики пар функций, которые в общем виде можно записать так:
$$ y_1 = f(x), quad y_2 = Af(x) $$
где $A gt 1$, произвольный положительный множитель.
Пусть A = 2.
|
Парабола: $y_1 = f(x) = x^2$ $ y_2 = 2f(x) = 2x^2 $ $y_2 = 2y_1 при x_2 = x_1$ График растягивается в 2 раза по оси OY |
 |
|
Гипербола: $ y_1 = f(x) = frac{4}{x}$ $y_2 = 2f(x) = frac{8}{x}$ $ y_2 = 2y_1 при x_2 = x_1$ График растягивается в 2 раза по оси OY |
|
|
Квадратный корень: $y_1 = f(x) = sqrt{x}$ $y_2 = 2f(x) = 2sqrt{x}$ $y_2 = 2y_1 при x_2 = x_1$ График растягивается в 2 раза по оси OY |
|
Теперь сравним пары функций с делением на A:
$$ y_1 = f(x), quad y_2 = frac{1}{A} f(x), quad A gt 1 $$
Пусть A = 2
|
Парабола: $y_1 = f(x) = x^2$ $ y_2 = frac{1}{2}f(x) = frac{x^2}{2}$ $y_2 = frac{1}{2}y_1 при x_2 = x_1$ График сжимается в 2 раза по оси OY |
 |
|
Гипербола: $ y_1 = f(x) = frac{4}{x}$ $y_2 = frac{1}{2}f(x) = frac{2}{x}$ $ y_2 = frac{1}{2}y_1 при x_2 = x_1$ График сжимается в 2 раза по оси OY |
|
|
Квадратный корень: $y_1 = f(x) = sqrt{x}$ $y_2 = frac{1}{2}f(x) = frac{sqrt{x}}{2}$ $y_2 = frac{1}{2}y_1 при x_2 = x_1$ График сжимается в 2 раза по оси OY |
|
При сравнении графиков двух функций
$$ y_1 = f(x), quad y_2 = Af(x), quad A gt 1 $$
график второй функции растягивается в A раз по оси OY по сравнению с графиком первой функции.
При сравнении графиков двух функций
$$ y_1 = f(x), quad y_2 = frac{1}{A} f(x), quad A gt 1 $$
график второй функции сжимается в A раз по оси OY по сравнению с графиком первой функции.
Заметим, что данные утверждения справедливы не только для рассмотренных функций, но и для любых других (синусов, косинусов, логарифмов и т.п.)
Примеры
Пример 1. Постройте в одной координатной плоскости графики функций:
$$ y = sqrt{x}, y = sqrt{3x}, y = sqrt{frac{x}{3}}, y = 3sqrt{x} $$
Сделайте выводы.
По сравнению с графиком $y = sqrt{x}$:
- график функции $y = sqrt{3x}$ сжимается в 3 раза по оси OX(←)
- график функции $y = sqrt{frac{x}{3}}$ растягивается в 3 раза по оси OX(→)
- график функции $y = 3sqrt{x}$ растягивается в 3 раза по оси OY(↑)
Пример 2*. Постройте в одной координатной плоскости графики функций:
$$ y = f(x), y = f(2x), y = f Biggl(frac{x}{2}Biggr), y = 2f(x) $$
где $f(x) = x^2+3x+2$
Сделайте выводы.
Исходная функция $y = f(x) = x^2+3x+2$
Остальные функции
$$ y = f(2x) = (2x)^2+3 cdot (2x)+2 = 4x^2+6x+2 $$
$$ y = fBiggl(frac{x}{2}Biggr) = Biggl(frac{x}{2}Biggr)^2+3 cdot Biggl(frac{x}{2}Biggr) +2 = frac{x^2}{4}+ frac{3}{2} x+2 $$
$$ y = 2f(x) = 2x^2+6x+4 $$
Получаем:
По сравнению с графиком $y = f(x) = x^2+3x+2$:
- график функции y = f(2x) сжимается в 2 раза по оси OX(→)
- график функции $y = f left(frac{x}{2}right)$ растягивается в 2 раза по оси OX(←)
- график функции y = 2f(x) растягивается в 2 раза по оси OY(↑)
Рейтинг пользователей
План урока:
Понятие функции
Растяжение и сжатие графиков функций
Параллельный перенос графиков функций
Гипербола и обратная пропорциональность
Дробно-линейная функция
Понятие функции
Понятие функции в школьной программе впервые встречается в 7 классе, поэтому настоятельно рекомендуем перечитать посвященный этой теме урок. Напомним, что функцией (в учебной литературе может использоваться сокращение ф-ция) называется соответствие между элементами двух множеств или, другими словами, зависимость между двумя величинами. Чаще всего в алгебре рассматриваются числовые ф-ции, которые заданы аналитически, то есть формулой. В качестве примера можно привести запись
у = 5х + 7
Здесь х – это независимая переменная, или аргумент, а у – зависимая величина, или просто функция. Принципиально важно, что каждому значению аргумента соответствует только одно значение зависимой величины. Часто в математике используют запись
y = f (x)
Она читается как «игрек равен эф от икс» и означает, что величина у как-то зависит от х. По сути, она равноценна записи
у = у (х)
Если в скобках стоит конкретное число, то запись означает значение ф-ции при этом значении аргумента.
Так, если
у(x) = 4x2
то
у (5) = 4•52 = 100
у (10) = 4•102 = 400
У каждой ф-ции есть область допустимых значений (используется сокращение ОДЗ), или область определения функции. Это те значения аргумента, при которых ф-ция определена. Здесь возможны два случая. В первом область определения указывается прямо. Например, если рассматривается функция у = х4 при значениях х от 1 до 3, то и областью определения будет всё множество чисел от 1 до 3. Для обозначения области определения используется запись D(y) или D(f). При изучении неравенств мы уже познакомились с такими объектами, как числовые промежутки. Именно с их помощью указывают ОДЗ.
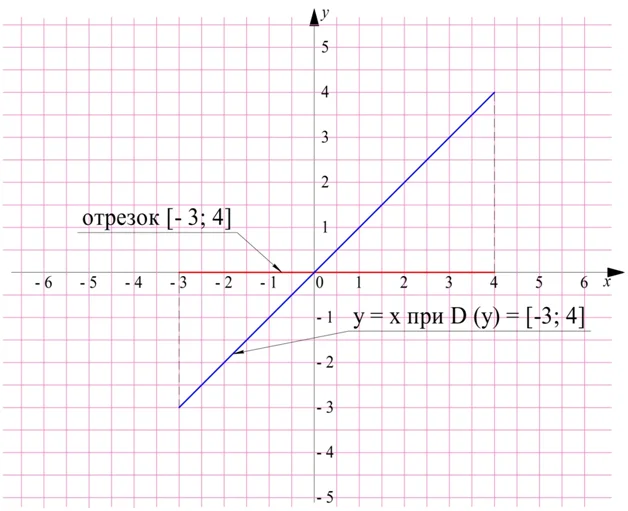
Пример. Постройте график функции у = х, если D(y) = [– 3; 4].
Решение. Ф-ция у = х – это линейная функция, мы уже умеем строить их графики (они представляют собой прямую линию). Выглядеть он будет так:
Однако в условии также есть запись D (y) = [– 3; 4], которая означает, что ф-ция определена только при х от – 3 до 4. С учетом этого условия график несколько преобразится:
Грубо говоря, часть графика, которая не входит в область определения, просто «отрезана».
Значительно чаще область определения явно не указывается. В этом случае предполагается, что ф-ция определена во всех точках числовой прямой, в которых ее вообще возможно вычислить. Например, ф-цию у = 9х3 – 47 можно вычислить при любом значении х, поэтому ее область определения – вся числовая прямая, то есть D(y) = (– ∞; + ∞).
А когда же вычислить функцию невозможно? К этому уроку нам известны две таких ситуации:
- когда в операции деления делителем является ноль, либо ноль является основанием степени с отрицательным показателем;
- когда под знаком корня находится отрицательное выражение.
Например, вычислить ф-цию у = 5/х при х = 0 невозможно, поэтому ее область определения – вся числовая прямая, кроме нуля, то есть
D(y) = (– ∞; 0)⋃(0; + ∞)
Функция
имеет область определения D(y) = [5; + ∞), так как при х< 5 подкоренное выражение становится отрицательным.
Также выделяют такое понятие, как область значений функции. Это множество всех значений, которые может принимать ф-ция. Проще всего проиллюстрировать это понятие на графике произвольной ф-ции:
Для обозначения области значений используется запись Е(у) или Е(f). Так, у ф-ции у = х2 при D(y) = [– 2; 2] областью значений будет промежуток [0; 4], то есть Е(у) = [0; 4]. Это видно из графика функции:
Ещё раз напомним, что область определения и область значения функции указываются с помощью числовых промежутков.
Теперь перейдем к тем понятиям, которые не изучались ранее. Первое из них – это нули функции. Так называют те значения аргумента, при которых функция обращается в ноль.
Так, у ф-ции
у = х2 – 9х + 20
есть два нуля, х = 4 и х = 5. Убедиться в этом можно подстановкой:
у(4) = 42 – 9•4 + 20 = 0
у (5) = 52 – 9•5 + 20 = 0
Для нахождения нулей ф-ции у = f(x) надо просто решить уравнение
f(x) = 0
Например, чтобы найти нули приведенной выше функции
у = х2 – 9х + 20
надо решить уравнение
х2 – 9х + 20 = 0
Сделаем это, ведь мы уже умеем решать квадратные уравнения:
D = (– 9)2 – 4•1•20 = 1
На графике нули ф-ции – это те точки, в которых график пересекает ось Ох:
Ещё одно новое понятие – промежутки знакопостоянства. Так называют промежутки числовой прямой, на которых ф-ция либо только положительна, либо только отрицательна. Для наглядности покажем их на графике:
Пусть есть ф-ция у = f(x). Для нахождения промежутков знакопостоянства необходимо решить неравенства f(x)>0 и у = f(x)< 0.
Пример. Найдите промежутки знакопостоянства функции у = 3х – 36
Решение. Решим неравенство 3х – 36 > 0:
3х> 0
3х >36
х > 12
Получаем, что функция положительна на промежутке (12; + ∞).
Аналогично решив неравенство 3х – 36 < 0, получим, что ф-ция отрицательна на промежутке (– ∞; 12).
Пример. Дана функция у = х2 – 5х. Найдите такое значение величины а, для которого выполняется условие у(а) = у(а + 2).
Решение. Очевидно, что у(а) = а2 – 5а. Теперь вычислим у(а + 2):
у(а + 2) = (а + 2)2 – 5(а + 2) = а2 + 4а + 4 – 5а – 10 = а2 – а – 6.
Теперь приравняем значения у(а) и у(а + 2):
а2 – 5а = а2 – а – 6
а2 – 5а – а2 + а = – 6
– 4а = – 6
а = 1,5
Убедимся, что мы нашли требуемое значение а:
у(1,5) = 1,52 – 5•1,5 = 2,25 – 7,5 = – 5,25
у(1,5 + 2) = у(3,5) = 3,52 – 5•3,5 = 12,25 – 17,5 = – 5,25
Ответ: 1,5
Растяжение и сжатие графиков функций
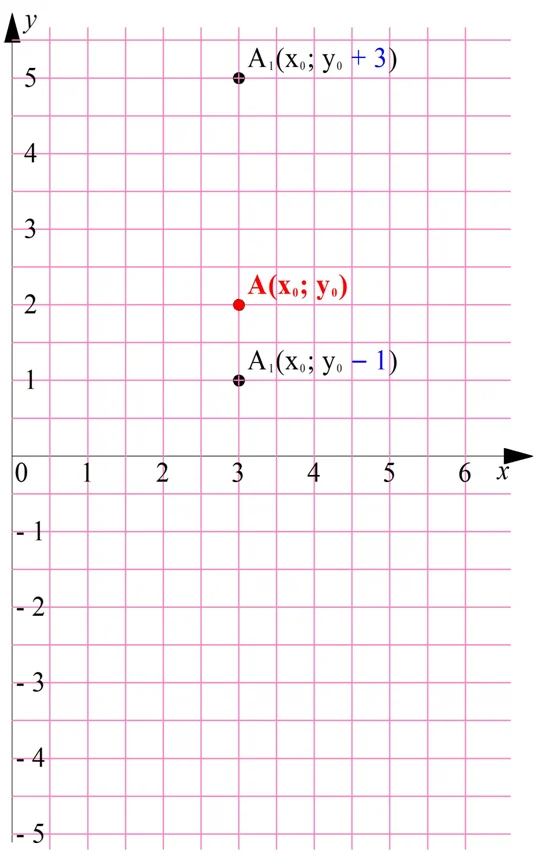
Пусть на координатной плоскости есть точка А с координатами (х0; у0). Куда переместится эта точка, если ее ордината (то есть у0) увеличится, например, в два или в три раза? Она отодвинется от оси Ох. Если же ее ордината уменьшится, то точка приблизится к оси. Наконец, если ордината поменяет знак, то точка, изначально, лежащая выше оси, окажется ниже её. Проиллюстрируем это на картинке:
Пусть есть пара функций у(х) и g = k•у(х), где k– какое-то постоянное число (константа), не равная нулю. Примерами таких пар являются:
- у = х и g = 3х (здесь k = 3);
- у = х2 и g = – 0,7х2 (k = – 0,7)
- y = x2 + 2x + 4 и g = 4(x2 + 2x + 4) = 4х2 + 8х + 16 (k = 4).
Посмотрим, как связаны графики таких функций. На рисунке красным цветом показана функция у(х), а синим g = 2у(x):
При любом значении аргумента выполняется условие g(х) = 2у(х). Это значит, что ордината (координата у) каждой точки графика g(х) вдвое больше, чем ордината соответствующей точки графика у(х). В частности, отрезок АА2 вдвое длиннее отрезка АА1:
АА2 = 2АА1
Аналогично можно записать, что
BB2 = 2BB1
Таким образом, график g(x) выглядит так, будто бы график у(х) «растянули» в 2 раза. Каждая точка «переезжает» на новое место, сдвигаясь по вертикали. Так, если точка А1 имела координаты (– 6; 2), то при растяжении графика функции она получит координаты (– 6; 4), то есть ее координата у увеличится вдвое. Точка B1 имела координаты (2; – 2), а в графике g(х) занимает позицию (2; – 4).
Убедимся в этом на примере ф-ций у = х2 и g = 2х2:
- при х = 1 имеем у(1) = 12 = 1; g(х) = 212 = 2
- при х = 2 получаем у(2) = 22 = 4 и g(x) = 222 = 8
- при х = 3 у(3) = 32 = 9 и g(3) = 232 = 18
В общем случае говорят, что график функции g(х) = ky(x) получается растяжением графика у(х) в k раз.
Пример. Функция у(х) задана графически:
Постройте график функции g(х) = 3у(х).
Решение. Каждую точку отодвинем от оси Ох, увеличив координату у точек в 3 раза:
Если коэффициент k находится в пределах 0 < k < 1, то график не растягивается, а наоборот, «сжимается». Точки перемещаются ближе к оси Ох.Для примера посмотрим на график ф-ции у = 0,5х2. Он может быть получен сжатием графика функции у = х2:
При сжатии графика каждая точка параболы приближается к оси Ох, при этом ордината точек уменьшается вдвое. Так, точка А2 с координатами (3; 9) переходит в точку А1 с координатами (3; 4,5).
Отдельно стоит рассмотреть случай, при котором коэффициент k является отрицательным. В этом случае график отображается симметрично относительно оси Ох. Те точки, которые имели изначально положительную ординату и находились выше Ох, в результате получают отрицательную ординату и оказываются ниже оси Ох. Покажем на рисунке графики ф-ций у = х2 и у = – х2 (то есть k =– 1):
Если же, например, коэффициент k = – 2, то надо и растянуть график, и перевернуть его относительно оси Ох. В частности, так выглядит график у = – 2х2:
Параллельный перенос графиков функций
Теперь посмотрим, как передвинется отдельная точка на координатной плоскости, если к ее ординате добавить какое-нибудь число. Если это число положительное, то точка поднимется выше, а если отрицательное, то она опустится:
Это означает, что если к какой-нибудь функции добавить некоторое число, то график функции переместится вверх или вниз. Для примера построим графики функций у = х2 + 2 и у = х2 – 5:
График у = х2 + 2 представляет собой тот же график у = х2, то есть параболу, который подняли на две единицы вверх. График у = х2 – 5 получен за счет сдвига вниз на 5 единиц этой же параболы. Подобное перемещение называют параллельным переносом графика функции.
Параллельный перенос возможен не только в вертикальном, но и в горизонтальном направлении. Для такого перемещения надо изменить абсциссу точки, а не ординату:
Аналогично может сдвинуться не только точка, но и целый график функции. Если вместо аргумента х подставить в ф-цию величину (х +n), то график сместится на n единиц влево.
Проиллюстрируем это с помощью ф-ций у = х2 и g = (х + 3)2. Будем вычислять значения обеих ф-ций в некоторых точках, причем для функции g будем брать значения х, меньше на три единицы:
у(0) = 02 = 0 и g(– 3) = g(– 3 + 3)2 = 02 = 0
у(– 1) = (– 1)2 = 1 и g(– 4) = g(– 4 + 3)2 = (– 1)2 = 1
у(– 2) = (– 2)2 = 4 и g(– 5) = g(– 5 + 3)2 = (– 2)2 = 4
Видно, что одинаковые значения ф-ции принимают тогда, когда аргумент у ф-ции g меньше на 3. Это значит что если сместить точку графика у = х2 на 3 единицы влево, по она попадает на график g = (х + 3)2.
Точка А1 сдвинулась влево на 3 единицы и перешла в точку А2. Аналогично точка В1 отобразилась в точку В2.
Пусть в общем случае есть функции у = у(х) и g(x) = у(х +n), где n – некоторое постоянное число. Значение у(х) в точке х0 обозначается как у0. Теперь найдем значение g(x) в точке (х0 – n):
g(х0–n) = у(х0 –n+n) = y(x0).
Получили, то же самое значение, что и у у(х). Покажем это на рисунке:
Рассмотрим теперь случай, когда график сдвигается вправо. Для этого из аргумента исходной функции надо вычесть какое-то число. На рисунке показаны графики функций у = 2х и у = 2(х – 4):
Каждая точка исходного графика (например, А1) «переехала» на 4 единицы вправо.
Надо понимать, что иногда один график можно получить из другого в несколько переходов. Пусть надо построить график у = – (х – 4)2 + 5. Его можно получить из обычной параболы у = х2 в три шага.
Сперва строим график у = (х – 4)2. Вершина параболы, как и все остальные точки, сместится на 4 позиции вправо:
Далее построим график у = – (х – 4)2. Для этого его надо отобразить симметрично относительно оси Ох (ось симметрии параболы не сдвигается, но ее ветви будут направлены вниз, а не вверх):
Последний шаг – это построение графика у = – (х – 4)2 + 5. Его можно получить, подняв предыдущий график на 5 единиц вверх:
Гипербола и обратная пропорциональность
Ранее мы уже строили графики степенных функций. Однако мы рассматривали только случаи, при которых показателем в степени являлось натуральное число. Теперь же изучим функцию у = х– 1. Напомним, что по определению отрицательной степени
Найдем область определения функции у = 1/х. Ясно, что аргумент не может равняться нулю, так как иначе получим деление на ноль:
у(0) = 1:0
При любых других значениях х значение у вычислить можно, а потому областью определения будет промежуток (– ∞; 0)⋃(0;+ ∞).
При положительных значениях аргумента ф-ция также будет положительной:
у(5) = 1:5 = 0,2
у(2) = 1:2 = 0,5
у(10) = 1:10 = 0,1
При отрицательных х величина у будет становиться отрицательной:
у(– 5) = 1:(– 5) = – 0,2
у(– 2) = 1:(– 2) = – 0,5
у(– 10) = 1:(– 10) = – 0,1
Это означает, что график ф-ции будет располагаться в I и III четвертях.
Можно заметить, что чем больше х, тем ближе у к нулю:
у(1) = 1
у(10) = 0,1
у(100) = 0,01
И наоборот, чем ближе х к нулю, тем больше у:
у(0,1) = 1:0,1 = 10
у(0,01) = 100
у (0,001) = 1000
При этом у не может равняться нулю. Действительно, дробь равна нулю только тогда, когда ее числитель равен нулю. Однако варьируя х, мы меняем только знаменатель, а в числителе остается единица. Поэтому областью значений функции у = х– 1 является промежуток (– ∞; 0)⋃(0;+ ∞).
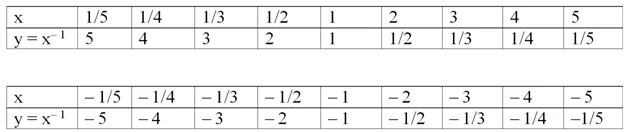
Для построения графика найдем некоторые точки графика и занесем их в таблицу. Мы построим две таблицы – одну для положительных х, другую для отрицательных:
Теперь можно посмотреть и на сам график:
Первое, что бросается в глаза – это то, что график не представляет собой единую, непрерывную линию. Он разбит на две ветви, одна из которых располагается в III четверти, а другая – в I четверти. Такой «разрыв» связан с тем, что ноль не входит в область определения ф-ции.
Также можно заметить симметричность графика. Действительно, одна из ветвей является симметричным отображением второй ветви.
Построенный нами график называется гиперболой.
На координатной плоскости есть две прямые линии, к которым гипербола приближается, но при этом он не касается их. Это оси Ох и Оу. Для наглядности покажем их штриховой линией:
В математике подобные линии называют асимптотами функции. Горизонтальная асимптота прямая соответствует линии х = 0, а вертикальная асимптота линии у = 0.
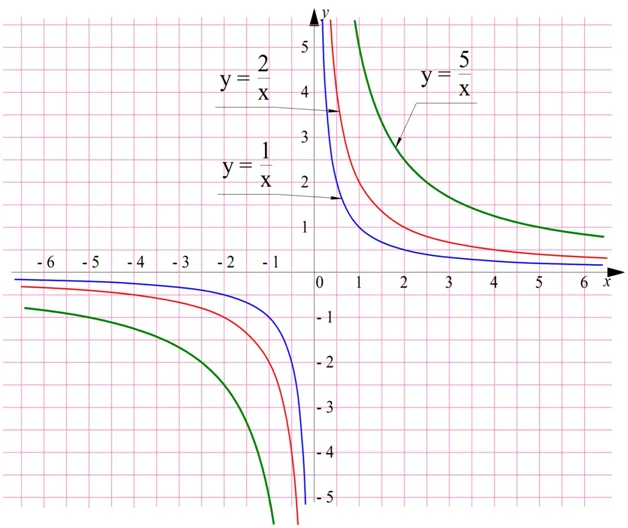
Зная, как выглядит график у = 1/х, мы можем построить и другие, схожие с ним графики для ф-ций у = k/х, где k– это некоторое число. Их можно получить из гиперболы, используя сжатие и растяжение графиков. Если коэффициент k больше единицы, то график «отдаляется» от осей Ох и Оу:
Все эти линии являются примерами гипербол. Если коэффициент k отрицательный, то графики переворачиваются относительно оси Ох и занимают II и IV четверти:
Все приведенные зависимости вида у = k/х называют обратными пропорциональностями.
Примерами обратной пропорциональности являются ф-ции:
Обратная пропорциональность очень часто встречается в жизни. Так, время, затрачиваемое на поездку на автомобиле, обратно пропорционально средней скорости движения. Количество товара, которое можно купить на одну зарплату, обратно пропорционально стоимости этого товара.
Дробно-линейная функция
Теперь рассмотрим несколько более сложные ф-ции, чьи графики, однако, также представляют собой гиперболу. Пусть есть ф-ция вида
Как будет выглядеть ее график? Для ответа на этот вопрос выполним преобразование:
Здесь мы в числителе и знаменателе добавили и сразу вычли слагаемое 2.Этот прием помог нам выделить целую часть из дроби. В результате мы получили ф-цию, график которой можно получить с помощью двух параллельных переносов графика у = 6/х. Сначала график сместится на две единицы вправо:
На следующем шаге график поднимется на единицу вверх:
Стоит обратить внимание, что при таком передвижении гиперболы передвигаются и асимптоты графика гиперболы:
Функция
представляет собой дробь, являющуюся отношением двух линейных многочленов, х + 3 и х – 2. В математике подобные ф-ции называют дробно-линейными функциями. В качестве примеров дробно-линейных функций можно привести:
Из любой дробно-линейной функции можно выделить целую часть. Покажем это на нескольких примерах:
Во всех этих случаях график дробно-линейной функции можно построить с помощью двух параллельных переносов гиперболы.
Однако есть одно исключение. Иногда при выделении из дроби целой части дробной части не остается вовсе, то есть линейные полиномы можно сразу сократить. Например:
Графиком таких функций являются прямые горизонтальные линии. Однако на них должна быть одна «исключенная». Действительно, пусть надо построить график ф-ции
Проведя преобразования, получим
то есть у = 2. Однако в знаменателе дроби не может стоять ноль. Если же подставить в дробь х = – 2, то получим деление на ноль:
Поэтому график ф-ции будет выглядеть так:
Итак, по итогам урока мы узнали:
- как растягиваются и сжимаются графики;
- как графики функций переносятся вверх-вниз и влево-вправо;
- что такое обратная пропорциональность и как выглядит ее график – гипербола;
- как выглядит дробно-линейная функция, и каким образом ее график можно получить из гиперболы с помощью параллельных переносов.
Содержание
Преобразование графиков

Литература
-
Генденштейн. Наглядный справочник по математике с примерами 2009 (с.16) – показаны все преобразования с примерами
-
Геометрические преобразования графиков функций, Танатар И.Я., 2012 MЦHMO – подробное изложение, 150 страниц, есть упражнения и ответы.
6 правил
Пусть C – число, большее нуля (C > 0).
График у = f(x) + C – получается параллельным переносом графика функции у = f(x) на C единиц вверх.
График у = f(x) – C – получается параллельным переносом графика функции у = f(x) на C единиц вниз.
График у = f(x+C) – получается параллельным переносом графика функции у = f(x) на C единиц влево.
График у = f(x-C) – получается параллельным переносом графика функции у = f(x) на C единиц вправо.
График у = -f(x) получается симметрией относительно оси абсцисс
График у = а f(x), где а>0 получается растяжением от оси абсцисс в а раз если а>1 или сжатием графика до оси абсцисс если 0<a<1 (то есть абсциссу не трогать, а ординату каждой точки умножить на коэффициент)
Правила преобразования графиков функций легко запоминаются, но если вы всё же не уверены в результате, проверьте его по одной-двум хорошим точкам. Эти правила, разумеется, общие для всех функций, а не только для тех, которые изучают в школе.
Учебники:
Алгебра 9 класс
Подробнее
Похоже на игру в слова ВОЛК – полк – пола – поза – КОЗА.
При переходе от одной функции к другой может произойти так называемое «изменение по x» и «изменение по y».
При изменении по y новая функция полностью содержит старую.
$$f(x) = x^2; g(x) = x^2+3 = f(x)+3$$
При изменении по x новая функция не содержит старую функцию в исходном виде, а в измененном.
$$f(x) = x^2; g(x) = (x+7)^2$$
Пример. Изменение в данном случае можно рассматривать и x и по y: $g(x)= (5x)^2 = 25 cdot x^2 = 25 cdot f(x)$, но только после преобразования, которое не всегда очевидно.
| Изменение по x [не естественные или внутренние] |
Изменение по y [естественные или внешние] |
|
|---|---|---|
| Сдвиг (параллельный перенос) |
Движение графика вдоль оси Ox влево и вправо f(x – 2) – вправо на 2 f(x + 2) – влево на 2 |
Движение графика вдоль оси Oy вверх и вниз f(x) – 2 – вниз на 2 f(x) + 2 – вверх на 2 |
| Деформация (масштабирование) |
сжатие и растяжение вдоль оси Ox f(kx), k > 0 k > 1 – сжатие k < 1 – растяжение |
сжатие и растяжение вдоль оси Oy kf(x), k > 0 k > 1 – растяжение k < 1 – сжатие |
| Отражение (преобразование симметрии) |
f(-x) – симметричное отражение относительно оси Oy | -f(x) – симметричное отражение относительно оси Ox |
Пример. $h(x) = 5sqrt{x}$ — растяжение графика $f(x) = sqrt{x}$ по оси Oy в 5 раз. Это значит, что ордината каждой точки графика увеличилась в 5 раз (при той же абсциссе).

Задачи ДПА-9 (2014): 9.1.5, 11.1.4, 14.1.8, 15.1.7, 19.1.4, 26.1.4, 29.1.6, 47.1.7, 49.1.5, 51.1.4, 55.1.7, 59.1.4, 66.1.4, 69.1.6.
Таблица преобразований
Нелин 10 2010. Даны подробные комментарии по каждому типу преобразований





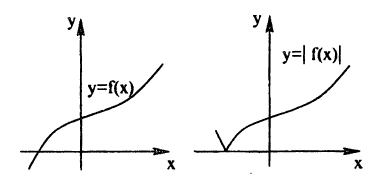
Преобразование графика с модулем
$$y = |f(x)|$$
-
При f(x) > 0 — график остаётся без изменений,
-
при f(x) < 0 — график симметрично отражается относительно оси абсцисс.
$$y = f(|x|)$$
-
При x > 0 — график остаётся без изменений,
-
при x < 0 — график симметрично отражается относительно оси ординат.
$$|y| = f(x)$$
-
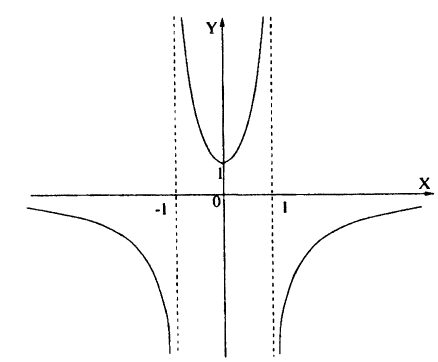
Данная кривая не будет являться функцией. Верхняя часть графика (распoлагается в I и IV координатных четвертях) остается без изменений, а нижняя (находящаяся в II и III четверти) исчезает, вместо нее симметрично оси абсцисс (OX) отображается верхняя часть графика

Когда под модулем только x, то действуем по правилу.
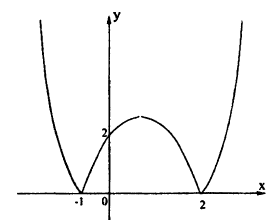
Когда под модулем выражение, то, думаю, надо рассматривать области где подмодульное выражение больше 0 и меньше 0 и строить их отдельно. Аналогично поступать если модулей несколько. В данном случае отдельно построить график для x >= -2 и x < -2.
Мерзляк 10 2018 предлагает преобразовывать, см далее, однако как объяснить ученику последовательность действий – почему в одних случаях сначала берем модуль, а потом двигаем график влево-вправо, а в других случаях – наоборот.
Пример. 


Модуль в учебниках считают не самостоятельной функцией (как корень, параболу, гиперболу), а видом преобразования (как паралельный перенос, сжатие-растяжение). Поэтому график функции y=|x| – это не птичка, а прямая, у которой отражена часть в отрицательной полуплоскости.
Кстати, y=|x| можно трактовать и как внутреннее (по x) и как внешнее преобразование (по y). График, разумеется, получается один и тот же.
Пример
Генденштейн

Поскольку здесь нет растяжений-сжатий, то почти безразлично в каком порядке выполнять отражения и сдвиги. Но даже в этом примере если параболу сначала отразить по оси x (взять модуль функции), а потом сдвинуть вниз на 1 единицу – то результат будет неверный. Таким образом, сначала нужно выполнить сдвиги, потом отражения.
Пример
Генденштейн

Пример
Генденштейн

Композиция преобразований
Если нужно скомбинировать только параллельные переносы, чтобы построить график функции, то всё равно в каком порядке их выполнять, и всё равно, что переносить – оси координат или кривые. Но если нужно построить график сложной функции, используя и перенос, и растяжение-сжатие, и отражения, то следует тщательно соблюдать порядок выполнения операций.
К примеру, квадратичная функция $y=- frac{1}{3}(x+frac{2}{3})^2+2$ представляет собой квадратичную параболу $y=x^2$, сжатую втрое относительно оси ординат, симметрично отображенную относительно оси абсцисс, сдвинутую против направления этой оси на 2/3 единицы и сдвинутую по направлению оси ординат на 2 единицы.

Другое объяснение
При построении графика функции необходимо:
-
выделить основную функцию, построив ее график;
-
постепенно преобразовывая основной график, соблюдая правила «внешних» и «внутренних» преобразований.
К внешним преобразованиям относятся действия, происходящие со всей функцией. Это y = f(x) + C, y = kf(x). Все изменения происходят со ВСЕЙ функцией, то есть внешне. Движение графика происходит относительно оси ординат (Оy).
Внутренними преобразованиями являются y = f(x+C), y = f(kx). Все преобразования осуществляются внутри функции с ее аргументом. Изменяется сам аргумент функции – ее внутренность. Движение графика происходит относительно оси абсцисс (ОХ).
Основной навык, который вам надо освоить – это отличать внутренние преобразования от внешних.
Последовательность преобразований при построении графиков
Пусть задан график функции $y = f(x)$ и нужно построить график функции $y = m·f(kx + l) + n$, где k, l, m, n – числа.
-
Записываем формулу функции в виде $y = m·f(k·(x + l/k))$, т.е. выносим за скобки коэффициент при х в аргументе функции.
-
Производим сжатие с коэффициентом k вдоль оси Ох к оси Oy. (Если k < 1, то получится растяжение от оси Oy.)
-
Если k < 0, то симметрично отображаем график относительно относительно оси Oy.
-
Осуществляем параллельный перенос (сдвиг) полученного графика на l/k единиц влево или вправо (в зависимости от знака, для положительного числа влево).
-
Производим растяжение с коэффициентом m от оси Oх (вдоль оси Оy). (Если m < 1, то получится сжатие к оси Ox.)
-
Если m < 0, то симметрично отображаем график относительно оси Ox.
-
Осуществляем параллельный перенос (сдвиг) полученного графика на n единиц вверх или вниз (в зависимости от знака, при n > 0 вверх).
Пример 8. Задан график функции $y = sqrt{x}$. Построить график функции $y = -0.5sqrt{3x – 12} + 2$.
-
Записываем формулу функции в виде $y = -0.5sqrt{3(x – 4)} + 2$
-
Строим известный график функции
-
Производим сжатие в 3 раза к оси Oy
-
(преобразование симметрии относительно оси Oy не требуется, т.к. k = 3 > 0)
-
Сдвигаем полученный график на 4 единицы вправо.
-
Производим сжатие в 2 раза (растяжение с коэффициентом 0,5) к оси Oх
-
Симметрично отражаем график относительно оси Ox
-
Сдвигаем последний на 2 единицы вверх. Получили требуемый график.

Проверим результат по «удобным» точкам. Например, x1 = 4 и x2 = 16.
Примеры
задача
Мерзляк Алгебра 2018 профильный

Подробнее
задача
Мерзляк Алгебра 2018 профильный

Подробнее

задача
Мерзляк Алгебра 2018 профильный

Подробнее
задача
Отношение двух прямых
1 случай. Прямые в числителе и знаменателе совпадают. Отношение равно 1 (константе)

2 случай. Прямые параллельны, угловые коэффициенты равны, или прямые пересекаются:
https://www.desmos.com/calculator/erywscteks


Алгебраически легко преобразовать отношение $frac {k_1x+b_1}{k_2x+b_2}$ к виду $kleft(frac a {x+b} + 1right)$, что означает сдвиг и сжатие гиперболы.
Прямые как бы не хотят делиться и изгибаются, отталкиваясь друг от друга.
Произведение двух прямых это парабола – прямые объединяются, но не совпадают, ветви смотрят в одну и ту же сторону. Чем больше аргумент, тем на большее расстояние расходятся ветви и захватывают пространство.
Сумма и разность двух прямых – это прямая или 0.
Функция, обратная параболе
https://www.desmos.com/calculator/vyxo7dxeex
Речь не о корне, а о функции $frac 1 {x^2+bx+c}$
Рассмотрим $1/x^2$. График состоит из двух ветвей. Там где парабола возрастает, там обратная парабола убывает. Вертикальная асимптота в нуле:


По форме ветви графика похожи на ветви обычной гиперболы, но немного иначе изогнуты. Ветви обратной функции находятся в верхней полуплоскости, если ветви параболы смотрят вверх (и в нижней – если вниз).

Опустим параболу вниз, был один ноль, теперь два нуля – и следовательно, две вертикальные асимптоты. Кусочек между асимптотами также переворачивается вверх ногами. Здесь как бы 4 ветви, две из которых срослись. Чем ниже парабола, тем ближе углы к прямым:


Случай когда у параболы нет нулей, а значит, обратная функция будет иметь только одну ветвь без вертикальных асимптот (горка). Чем выше поднимается парабола, тем площе будет горка:


Итак,
-
Если у параболы один нуль, тогда есть две ветви.
-
если у параболы нулей нет, то ветви сливаются в холмик или горку [у гиперболы $frac 1 {kx+b}$ такой ситуации не бывает, так как знаменатель всегда равен нулю в какой-то точке]
-
если у параболы два нуля, тогда есть три ветви – две похожи на гиперболические, одна похожа на параболу
$y=frac {1} {x^2 + px + q} =frac {1} {a(x-b)^2 + c} $
Верзьера Аньези
Верзьера Аньези — Википедия
https://www.desmos.com/calculator/dc7gspvnfw
Выгодский справочник по высшей математике, параграф 506
или верзие́ра Анье́зи (иногда ло́кон Анье́зи) – плоская кривая, геометрическое место точек $M$, для которых выполняется соотношение $ {frac {BM}{BC}}={frac {OA}{OB}}$, где $OA$ — диаметр окружности, $BC$ — полухорда этой окружности, перпендикулярная $ OA$. Своё название верзьера Аньези получила в честь итальянского математика Марии Гаэтаны Аньези, исследовавшей эту кривую.
Построение верзьеры:

Пьер Ферма в 1630 году нашёл площадь области между кривой и её асимптотой.
В 1703 году Гвидо Гранди, независимо от Ферма, описал построение этой кривой, а в работе 1718 года назвал её верзьерой (итал. Versiera, от лат. Versoria), так как в его конструкции использовалась функция синус-верзус (обращенный синус).
В прямоугольной системе координат:
$ y={frac {a^{3}}{a^{2}+x^{2}}}$
Кривая имеет один максимум — и две точки перегиба
Площадь под графиком $ S=pi a^{2}$ равна учетверенной площади производящего круга.

Объем тела вращения верзьеры вокруг асимптоты равен удвоенному объему тела вращения производящего круга
Объем тела вращения верзьеры вокруг оси симметрии имеет бесконечный объем
Строится окружность диаметра $ a$ и касательная к ней. На касательной выбирается система отсчёта с началом в точке касания. Строится прямая через выбранную точку касательной и точку окружности, противоположную точке касания. Эта прямая пересекает окружность в некоторой точке. Через эту точку строится прямая, параллельная касательной. Точка верзьеры лежит на пересечении этой прямой и перпендикуляра к касательной в выбранной точке.
Трамплин-рампа российского авианосца Адмирал флота Советского Союза Кузнецов образован верзьерой Аньези. Когда самолет сходит с рампы, он находится в идеальном угле атаки при скорости 180—200 км/ч (для Су-27). Теоретически, с рампы-трамплина может взлететь самолет любой взлетной массы.
Кадры взлета и посадки самолетов с авианесущего крейсера «Адмирал Кузнецов» – YouTube Запечатлены разгон и взлет самолетов с носового трамплина, а также их посадка при помощи аэрофинишера. трамплинный взлет и посадка на палубу являются сложнейшими элементами полета. При колоссальной перегрузке в 8-9 единиц пилот должен продемонстрировать ювелирную точность, чтобы попасть в небольшой участок между аэрофинишерами
Сумма прямой и гиперболы
Отношение двух парабол
https://www.desmos.com/calculator/bqhzu0uwul
Если ветви смотрят в одну сторону, то на бесконечности отношение стремится к положительной константе, а если в разные стороны – то к отрицательной константе. Это дает горизонтальные асимптоты на + и – бесконечности.


В точках, где знаменатель обращается в ноль (одна или две точки) получаем вертикальные асимптоты.
(не дописано)
Параллельный перенос, сжатие и растяжение графиков. Построение графиков с модулями.
Графики многих функций можно получить из ранее рассмотренных с помощью элементарных геометрических преобразований: параллельного переноса, сжатия, растяжения, симметричного отображения. Рассмотрим некоторые из этих преобразований. Для каждого из элементарных преобразований предлагается два способа построения графика: с помощью преобразования графика и с помощью преобразования системы координат. Обучающийся должен выбрать тот, который кажется ему проще и овладеть им. В каждом случае считается известным график функции у = f(х).
Параллельный перенос графиков
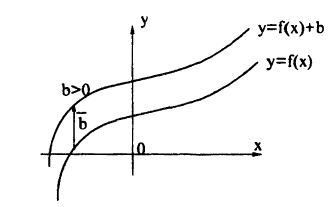
График функции у = /(x) + Ь получается из графика функции у = f(х) с помощью его переноса на вектор b = (0; b). Действительно, в этом случае ко всем ординатам графика у = f(х) прибавляется величина b, что означает сдвиг графика вдоль оси Оу. Если b > 0, то график функции у = f(х) переносится вверх параллельно оси Oy на b, если b < 0, то график функции у = f(x) переносится вниз параллельно оси Oy на |b| (рис. 49). Заметим, что вместо переноса графика, можно перенести в противоположном направлении ось Ox (если b > 0 — вниз, если b < 0 — вверх), прибавив ко всем значениям по оси Oy величину b.
Пример:
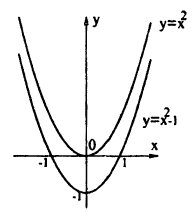
График функции у = x² — 1 (рис. 50) смещен на 1 вниз параллельно оси Oy относительно графика функции у = х².
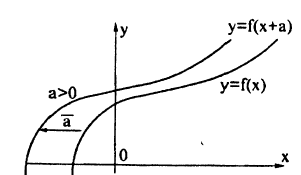
График функции у = f(x+a) получается с помощью переноса графика функции у = f(x) на вектор а = (—а;0). Действительно, перейдя к новым координатам X = х + α, Y = у параллельным переносом вдоль оси Ox на —а, заметим, что относительно новых координат получится исходный график функции Y = f(X). Если а > 0, то старые координаты получаются из новых сдвигом направо вдоль оси Ox на α, т.к. х = X — а. Если же сдвигать график, а не систему координат, то его нужно двигать в противоположном направлении — налево. Итак, если а > 0, то график функции у = f(x) переносится налево параллельно оси Ox на а, если а < 0, то график функции у = f(x) переносится направо вдоль оси Ox на ∣α∣ (рис. 51). Вместо переноса графика можно перенести в противоположном направлении ось Oy (если α > 0 — вправо, если α < 0 — влево), отняв от всех значений по оси Ox величину а.
Пример:
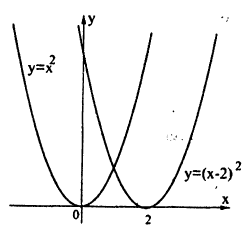
График функции у = (x- 2)² смещен на 2 ед. вправо параллельно оси Ox относительно графика функции у = х². (рис. 52).
Сжатие и растяжение графиков
График функции у = kf(x), где к ∈ R, получается с помощью ’’растяжения” графика функции у = f(x) в к раз в направлении от оси Ох. ’’Растяжение” здесь понимается как умножение на к ординат всех точек графика у = f(x)∙ При k > 1 это будет действительно растяжение в к раз от оси Ox вдоль оси Оу. При 0 < k < 1 это будет сжатие в 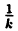
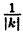
Вместо преобразования графика при k > 0 можно исправить значения по оси Оу, умножив их на k. При k < 0 в этом случае пришлось бы менять направление оси, что неудобно; лучше перевернуть график сверху вниз.
График функции у = f(kx), где k ∈ R, получается с помощью ’’сжатия” графика у = f(x) в к раз в направлении к оси Оу. ’’Сжатие” здесь понимается как деление на к абсцисс всех точек графика у = f(x). Действительно, если, например, f(1) =0, то, сделав замену X = kх, Y = у, получим, что функция у = f(kx) обращается в нуль при kх = 1, т.е. при
При k > 1 график функции у = f(x) сжимается в k раз к оси Oy вдоль оси Ох; при 0 < k < 1 график функции у = f(x) растягивается в 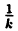
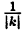
В частности, график функции у = f(-x) получается из графика функции у = f(-x) симметрией относительно оси Оу.
Вместо преобразования графика при k > 0 можно исправить значения по оси Ох, поделив их на k. При k < 0 в этом случае следует предварительно перевернуть график слева направо.
Пример:
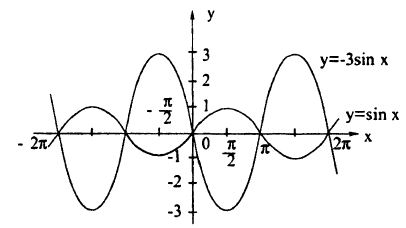
График функции у = cos 2х получается из графика у = cos х сжатием в 2 раза к оси Оу; график функции у = ln(—х) получается из графика у = ln х симметрией относительно оси Oy ( рис. 54).
Пользуясь изложенными методами, приведем последовательность преобразований при построении графика функции у = f(kx + b), если дан график функции у = f(x):
- нарисовать график функции у = f(x);
- получить график функции у = f(x + b), сдвинув исходный на вектор b = (-b; 0), как описано в п. 5.1;
- получить график функции у = f(kx + b), “сжав” предыдущий в к раз к оси Оу, как описано выше.
Пример:
Написать последовательность преобразований и построить график функции у = 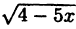
Решение:
Построение графика показано на рис. 55
Замечание:
Теперь понятно, что если функция у = f(x) периодическая с периодом Т, то функция у = К ∙ f(kx + b) + а тоже периодическая с периодом T₁ = 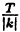
Построение графиков с модулями
График функции у = ∣f(x)∣ получается из графика функции у = f(x) следующим образом (рис. 56)
- все части графика функции у = f(x), лежащие ниже оси Ох, следует отобразить вверх симметрично относительно этой оси;
- оставшиеся внизу части исходного графика следует стереть.
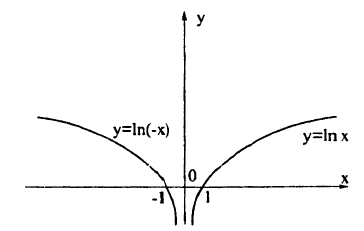
Действительно, по определению модуля действительного числа имеем:
(5.1)
Таким образом, те участки исходного графика, которые лежат не ниже оси Ox (f(x) ≥ 0), менять не нужно, а для тех участков, которые лежат ниже оси Ох, нужно построить функцию у = —f(x). В соответствии с п. 5.2 это получается симметричным отображением исходного графика относительно оси Ох. Заметим, что полученный график лежит не ниже оси Ох, что естественно, т.к. |f(x)| ≥ 0 для ∀x ∈ D(f).
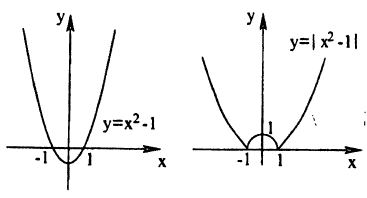
Пример:
Построение графика функции у = |х² — 1| показано на рис. 57.
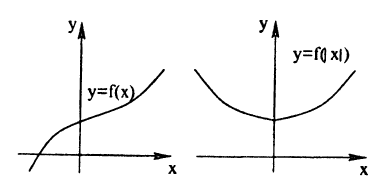
График функции у = f (|x|) получается из графика функции у = f(х) следующим образом (рис. 58):
- все части графика функции у = f(x), лежащие слева от оси Оу, следует стереть;
- о оставшуюся часть графика следует отобразить налево симметрично относительно оси Оу.
Действительно, по определению модуля действительного числа имеем:
(5.2)
Таким образом, не нужно изменять те участки исходного графика, для которых х ≥ 0, а для х<0 (слева от оси Оу) следует построить график функции у = f(—х). В соответствии с п. 5.2 это получается симметричным отображением исходного графика относительно оси Оу. Заметим, что полученный график симметричен относительно оси Оу, что естественно, т.к. функция у = f(|x|) четная (докажите самостоятельно).
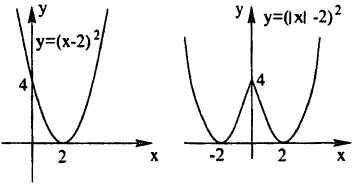
Пример:
Построение графика функции у = (|x| — 2)² показано на рис. 59
Элементарными методами можно строить эскизы графиков более сложных функций.
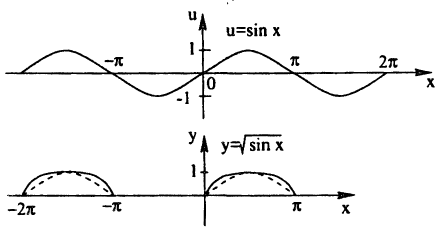
Пример:
Построить эскиз графика у =
Решение:
Построение графика показано на рис. 60. Заметим, что график отсутствует там, где sin х < О, так как D(x) = {x| sin х ≥ 0}
Кроме того, так как √u > и при 0 < u < 1, то график у = 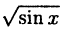
Построение графиков функций с примерами
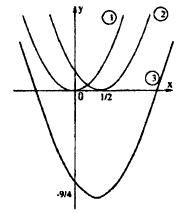
Пример:
C помощью элементарных преобразований постройте график функции: у = x² — х — 2.
Решение:
Выделим полный квадрат из правой части уравнения функции: у = x² — х — 2 ⇔ y = x²-x+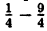
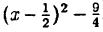
1) y =x²
2) у =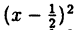
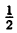
3) у = 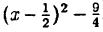
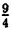
Пример:
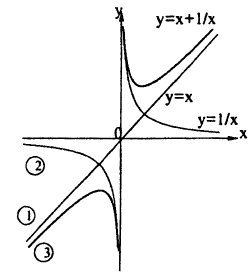
Используя сложение, деление функций, постройте график функции: у = х + 
Решение:
В одних осях координат нарисуем графики следующих функций (рис. 62):
1) у = х,
2) y=
3) y = x + 
Пример:
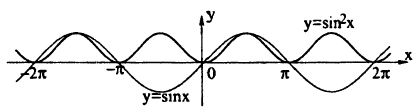
Постройте график сложной функции у = sin² х.
Решение:
В одних осях координат нарисуем графики функций:
1) y = sin x,
2) y = sin² х.
Учитывая, что квадрат числа меньшего единицы, меньше исходного числа, получим график (рис. 63)
Пример:
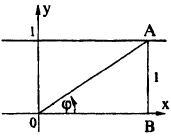
Постройте график функции в полярной системе координат: r = 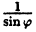
Решение:
Вычислим значения г для некоторых значений 
 |
0 | 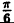 |
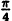 |
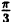 |
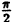 |
| r | ∞ | 2 | 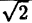 |
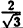 |
∞ |
Соединив плавной линией найденные точки, получим линию вдоль оси Ох, проходящую через точку (0;1). Докажем что эта линия — прямая (рис. 64). Действительно: из Δ ОAВ ⇒ cos
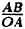
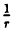
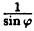
Пример:
Постройте линию, описываемую уравнением, у =
Решение:
Сначала построим график функции у =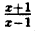
Наконец, строим линию описываемую уравнением у = 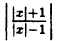
Пример:
Постройте линию, описываемую уравнением у =
Решение:
Для построения графика данного примера сначала постройте график функции у =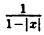
Ответ: рис. 68.
Пример:
Постройте линию, описываемую уравнением у = |х² — х -2|.
Решение:
Для построения графика данного примера сначала постройте график функции у = х² — х — 2. Затем отразите симметрично оси Ox ту часть графика, которая осталась снизу от оси Ох. Затем сотрите ту часть графика, которая расположена в нижней полуплоскости.
Ответ: рис. 69.
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат