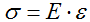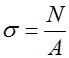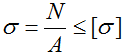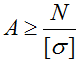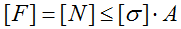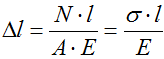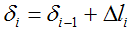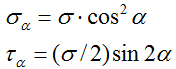Как найти растяжение проволоки

В приборах,
устройствах, машинах широкого применения
различного вида кабели, провода,
проволока. ГОСТ 10446-80. Проволока. Методы
испытания на растяжение – устанавливает
методы статических испытаний проволоки
цветных и черных металлов и их сплавов
диаметром до 16 мм на растяжение.
Определяются следующие характеристики
механических свойств:

• Предел
  пропорциональности;

• Предел упругости;

• Предел текучести;

• Временное
  сопротивление;

• Относительное
  удлинение;

• Относительное
  сужение после разрыва.

В качестве
образцов для испытаний берутся отрезки
проволоки с рабочей длиной 100-200 мм.
Измерение начальной и конечной расчетной
длины производят с точностью до 0,1 мм.
Диаметр проволоки более 1 мм измеряется
с точностью до 0,01 мм. Каждое измерение
в средней рабочей части проводят в двух
взаимно перпендикулярных направлениях,
за расчетное берут среднее арифметическое.

6.Порядок проведения испытаний образцов из проволки

1. На
   образце длиной 180-200 мм наносятся две
   метки на расстоянии l₀=100
   мм. Измеряется начальный диаметр
   проволоки в серединной части и вычисляется
   начальная площадь поперечного сечения
   А₀.

2. Образец закрепляется
   в зажимах. Для исключения краевых
   эффектов расстояние между зажимами
   устанавливается 115-120 мм.

3. На диаграммный
   барабан устанавливается диаграммная
   бумага, стрелка силоизмерителя на 0,
   перо записывающего устройства подводится
   к барабану до соприкосновения. Испытания
   проводятся для двух-трех образцов.

4. Включением
   двигателя разрывной машины осуществляется
   нагружение образца до разрыва. Диаграмма
   «усилие-абсолютная деформация»
   вычерчивается на бумаге автоматически.
   Шкала силоизмерительного прибора
   проградуирована в ньютонах. В зависимости
   от материала образца используют
   различные шкалы: А,В,С. переход от одной
   шкалы к другой осуществляется с помощью
   замены дисков на маятнике силоизмерительного
   механизма.

5. На
   полученной диаграмме F–l
   отмечаются характерные точки (см. раздел
   3 и рис.3.2);F_пц
   – нагрузка, соответствующая пределу
   текучести, H;
   F_т
   – нагрузка, соответствующая пределу
   пропорциональности, H;
   F_max
   – нагрузка, соответствующая пределу
   прочности, H.

6. Значения напряжений
   вычисляются по формулам:

_пц
=
,

_т
=
,

_пр
=
,

где
_пц
– предел пропорциональности, МПа;

_т
– предел текучести, МПа;

_пр
– предел прочности, МПа.

1. Допускаемое
   напряжение для пластических материалов
   определяется по пределу текучести:

[
] =
,

для хрупких
материалов по пределу прочности:

[
] =
,

где
n
– коэффициент запаса прочности, зависящий
от условий работы элемента конструкции,

качества
материала и других факторов. Значение
n
выбирается от 1,5 до 3,0.

Допускаемое
напряжение – это такое напряжение, при
котором гарантируется нормальное
функционирование элемента конструкции,
находящегося под действием расчетной
нагрузки.

1. Относительное
   удлинение 
   после разрыва

 =



100% ,

где

определяется из диаграммы,

l₀,
l_к
– начальная
длина и длина после разрыва.

1. Относительное
   сужение 

 =


100% ,

где
А₀,
А_К
– начальная площадь поперечного сечения
образца иплощадь поперечного сечения
образца после разрыва.

1. Полученные
   результаты вычислений заносятся в
   протокол испытаний (приложение 1).

Содержание

• Деформация агрегата
• Как рассчитывается растягивающее напряжение? (Примеры)
• Пример расчета
• Решенные упражнения
• – Упражнение 1
• Решение
• – Упражнение 2.
• Решение
• Ссылки

В Стресс-деформация Он определяется как сила, перпендикулярная площади на единицу площади, приложенная к объекту на его концах, чтобы оказывать на него тягу, благодаря которой он удлиняется. Его размеры – это сила / площадь, и в математической форме мы можем выразить это так:

τ = F / A

Единица усилия в Международной системе единиц такая же, как и для давления: паскаль, сокращенно Па, что эквивалентно 1 ньютону / м.².

При растягивающем напряжении у вас есть две силы, действующие в одном и противоположных направлениях, которые растягивают тело. Если изначально длина объекта была L_или, при приложении растягивающего напряжения новая длина равна L, а растяжение ΔL рассчитывается по формуле:

ΔL = L – L_или

Твердые объекты обладают большей или меньшей эластичностью, а это означает, что когда растягивающее напряжение исчезает, они возвращаются к своим первоначальным размерам.

Это происходит до тех пор, пока напряжение не настолько велико, чтобы вызвать необратимую деформацию. Резина, резина или резиновые материалы хороши для создания эластичных предметов, а волосы и кожа, среди прочего, также обладают этим качеством.

Деформация агрегата

При изучении того, как тела деформируются под действием напряжения, очень удобно определять понятие напряжение, безразмерная величина. Деформация обозначается греческой буквой δ (строчная «дельта») и рассчитывается следующим образом:

δ = ΔL / L_или

Деформация используется для сравнительной оценки деформации объекта под напряжением. Давайте посмотрим на это так: растянуть штангу длиной 1 метр на 1 см – это не то же самое, что растянуть штангу длиной 10 м на 1 см. В первом случае деформация значительно больше, чем во втором.

Как рассчитывается растягивающее напряжение? (Примеры)

Английский физик и современник Ньютона по имени Роберт Гук (1635-1703) исследовал упругие свойства тел и установил закон, носящий его имя. При этом приложенное напряжение связано с деформацией, испытываемой при небольшом напряжении:

Напряжение ∝ Деформация (единица)

Логично ожидать, что чем выше растягивающее напряжение, тем больше произойдет удлинение. Используя определения, данные выше:

τ ∝ δ

Константа пропорциональности, необходимая для установления равенства, обозначается Y и известна как модуль Юнга или модуль упругости, характерный для материалов:

τ = Y⋅δ

Модуль Юнга имеет те же единицы растягивающего напряжения, поскольку деформация безразмерна.

Итак, один из способов рассчитать растягивающее напряжение в теле с упругими свойствами – это измерить деформацию и узнать ее модуль Юнга. Эта сумма была определена экспериментально для многих материалов и занесена в таблицу.

Пример расчета

Предположим, что проволока из закаленной стали диаметром 3 мм подвергается растягивающему напряжению, и на ней висит груз 250 Н. Какова будет величина этого напряжения?

Что ж, мы можем использовать определение растягивающего напряжения как частное между силой, перпендикулярной поверхности, и площадью этой поверхности. Давайте сначала рассчитаем площадь, считая провод круглого сечения:

А = π. (d / 2)² =  π. (d² /4)

Диаметр провода 3 мм, и эти единицы необходимо перевести в метры:

г = 3 х 10^-3 м.

А = π. (3 х 10^-3 м)² / 4 = 7,07 х 10^-6 м².

Растягивающее напряжение создается грузом, подвешенным к проволоке, который прикладывается перпендикулярно поперечному сечению проволоки, поэтому:

τ = 250 Н / 7,07 x 10^-6 м² = 3,5 х 10 ⁷ Па

Паскаль – довольно маленькая единица, поэтому кратность не является чем-то необычным. Зная, что 1 мега-паскаль (МПа) равен 10⁶ паскаль, растягивающее напряжение составляет:

τ = 35 МПа

Решенные упражнения

– Упражнение 1

Модуль упругости стержня 4 х 10¹¹ Па. Какая деформация получается при приложении растягивающего усилия 420 МПа?

Решение

Используемое уравнение:

τ = Y⋅δ

С его помощью рассчитываем деформацию:

δ = τ / Y = 420 х 10⁶ Па / 4 x 10¹¹ Па = 0,00105

δ = ΔL / L_или

Следовательно, деформация ΔL равна:

ΔL = 0,00105 л_или

Если, например, стержень изначально был длиной 1 метр, при этом растягивающем напряжении он растягивается всего на 0,00105 м = 1,05 мм.

– Упражнение 2.

Стальная проволока имеет длину 1,50 м и диаметр 0,400 мм. Один конец прикреплен к потолку, а к другому прикреплен заземляющий отражатель. м = 1,50 кг, которое выпущено. Рассчитать:

а) Растяжение проволоки.

б) Деформация и процент деформации. Может ли провод порваться под тяжестью отражателя?

Решение

Проволока будет растягиваться, так как при подвешивании отражателя он подвергается растягивающему напряжению. Сила, вызывающая это усилие, – это вес отражателя.

Вес объекта массы m равен произведению массы на значение ускорения свободного падения, поэтому:

F = 1,50 кг x 9,8 м / с² = 14,7 Н

Площадь сечения провода нужна:

А =  π. (d² / 4) = π x (0,4 x 10-3 м) 2/4 = 1,26 x 10^-7 м².

На основе этих результатов рассчитывается усилие, прилагаемое грузом к проволоке:

τ = 14,7 Н / 1,26 x 10^-7 м² = 1,17 х 10⁸ Па

Проволока имеет упругие свойства, поэтому можно предположить, что выполняется закон Гука:

τ = Y⋅δ

Из таблицы модулей упругости находим, что для стали Y = 207 x 10⁹ Па. Кроме того, штамм бывает:

δ = ΔL / L_или

Подставляя в уравнение для усилия:

τ = Y⋅δ = Y⋅ (ΔL / L_или)

Следовательно, растяжка:

ΔL = L_или τ / Y =

= 1,50 м x 1,17 x 10⁸ Па / 207 x 10⁹ Па = 8,5 х 10^-4 m = 0,849 мм.

Деформация проволоки составляет:

δ = ΔL / L_или = 8,5 х 10^-4 м / 1,5 м = 5,652 х 10^-4

Если выразить это в процентах, то деформация единицы в процентах составляет 0,0565%, менее 0,1%, поэтому ожидается, что провод будет выдерживать вес отражателя хорошо, не ломаясь, поскольку деформация, которую он испытывает, не слишком велика по сравнению до исходной длины.

Ссылки

1. Бауэр, В. 2011. Физика для инженерии и науки. Том 1. Мак Гроу Хилл.
2. Бир, Ф. 2010. Механика материалов. Макгроу Хилл. 5-е. Издание.
3. Джанколи, Д. 2006. Физика: принципы с приложениями. 6-е. Эд Прентис Холл.
4. Сирс, Земанский. 2016. Университетская физика с современной физикой. 14-го. Ред. Том 1.
5. Валера Негрете, Дж. 2005. Заметки по общей физике. UNAM.