Артём Артёмович3,7 K
4 дек 2018
На динамометре есть шкала и стрелка, которая показывает силу воздействия. Если гвоорить о формуле, то F = mg, где F – сила (ньютоны), воздействующая на прибор, m – масса груза (кг), а g – ускорение свободного падения, для земли равное 9,8. Из формулы следует, что 100 г грузик будет действовать с силой примерно 1 ньютон.
308
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
Конспект по физике для 7 класса «Закон Гука. Динамометр». ВЫ УЗНАЕТЕ: Как формулируется закон Гука. Что такое коэффициент упругости пружины. Каким прибором измеряется сила. ВСПОМНИТЕ: Что такое сила? Каковы единицы силы? Что такое сила тяжести? Как рассчитать силу тяжести? Что такое сила упругости?
Конспекты по физике Учебник физики Тесты по физике
Закон Гука. Динамометр
Английский физик Роберт Гук, современник И. Ньютона, в 1660 г. экспериментально установил, как зависит сила упругости от деформации.
ЗАКОН ГУКА
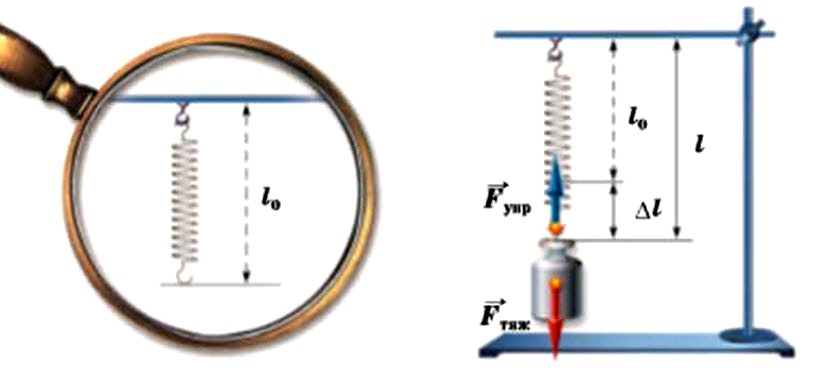
Проведём следующий опыт. К штативу подвесим пружину и измерим её длину. Пусть длина нерастянутой пружины равна l0. Если теперь к ней подвесить грузик, то пружина растянется и её длина станет равна l. Растяжение пружины равно Δl = l – l0. Чем тяжелее грузик, тем сильнее растягивается пружина и тем больше значение Δl.
Каждый раз при подвешивании груза пружина растягивается до определённого состояния, после чего движение груза прекращается и система приходит в состояние равновесия. Это означает, что сила тяжести, действующая на груз, компенсируется силой упругости, возникающей в пружине. Сила тяжести определяется по формуле Fтяж = mg. Следовательно, чем больше масса груза, тем больше значение силы тяжести, действующей на него, и соответственно больше значение силы упругости, уравновешивающей её. Тщательные измерения в данном опыте показывают, что растяжение пружины прямо пропорционально значению силы упругости.
Опыт подтверждает закон, названный в честь учёного, открывшего его,
законом Гука
: модуль силы упругости при растяжении (или сжатии) тела прямо пропорционален изменению длины тела.
Коэффициент пропорциональности в законе Гука называют коэффициентом упругости тела (стержня, пружины и т. п.). Он зависит от формы и размеров тела, а также от материала, из которого оно изготовлено. Коэффициент упругости в СИ выражается в ньютонах на метр (Н/м).
УПРУГАЯ И ПЛАСТИЧЕСКАЯ ДЕФОРМАЦИИ
Деформации, которые полностью исчезают, как только прекращается действие деформирующей силы, называют упругими. Деформации, которые не исчезают после прекращения действия деформирующей силы, называют пластическими. Если пружину растянуть, а затем отпустить, то она примет первоначальную форму. Но эту же пружину можно растянуть настолько, что после того, как её отпустят, она так и останется растянутой. Закон Гука справедлив только для упругой деформации, для пластических деформаций он не выполняется.
ДИНАМОМЕТР
Закон Гука лежит в основе действия прибора для измерения силы — динамометра (от греч. dinamis — сила и metron — мера). Принцип действия пружинного динамометра основан на сравнении любой силы с силой упругости пружины. На практике используют динамометры самого разного тина.
ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЗАКОНА ГУКА
Простейший пружинный динамометр (динамометр Бакушинского) состоит из пружины с двумя крючками, укреплённой на дощечке. Дощечка снабжена шкалой, а к нижнему концу пружины прикреплён указатель.
Построим график зависимости силы упругости от деформации пружины динамометра.
Для этого будем последовательно подвешивать к динамометру грузики определённой массы и измерять соответствующие значения силы упругости и растяжения пружины. Так как сила тяжести, действующая на тело массой 1 кг, равна 9,8 Н, то сила, равная 1 Н, будет действовать на тело, которое в 9,8 раза легче. Масса этого тела 102 г. Под влиянием силы тяжести, действующей на груз, пружина динамометра растягивается на Δl1 = 2,5 см. Нанесём на график соответствующую точку (зелёным цветом). Подвесим к крючку ещё один такой же груз и повторим описанный опыт. Суммарная масса груза в этом случае равна 204 г, а деформация — Δl2 = 5 см. Нанесём соответствующую точку на координатную плоскость. Проделаем аналогичные действия для трёх грузов. Можно увидеть, что все три точки лежат на одной прямой.
Как по графику определить значение коэффициента упругости пружины? По закону Гука k = Fупр / Δl. Если взять любую точку, лежащую на прямой, и определить её координаты, то на оси абсцисс мы получим значение Δl, а по оси ординат — значение Fупр. Поделив одно значение на другое, получим искомую величину.
Повторив описанный опыт с другой пружиной, получим график другой прямой (синего цвета), которая отличается от предыдущей углом наклона к оси абсцисс. Чем больше коэффициент упругости пружины, тем угол наклона больше.
Вы смотрели Конспект по физике для 7 класса «Закон Гука. Динамометр»: Как формулируется закон Гука. Что такое коэффициент упругости пружины. Каким прибором измеряется сила. Что такое сила? Каковы единицы силы? Что такое сила тяжести? Как рассчитать силу тяжести? Что такое сила упругости?
Вернуться к Списку конспектов по физике (В оглавление).
Сила упругости. Закон Гука
- Виды деформаций
- Закон Гука
- Измерение силы с помощью динамометра
- Задачи
п.1. Виды деформаций
Под действием силы все тело или отдельные его части приходят в движение.
При движении одних частей тела относительно других происходит изменение формы и размеров.
Деформация – это изменение взаимного положения частиц тела, связанное с их перемещением друг относительно друга под действием приложенной силы, при котором тело изменяет свою форму и размеры.
 |
К простейшим видам деформации относятся:
|
Различают упругие (обратимые) и неупругие (необратимые) деформации.
Деформация является упругой, если, после прекращения действия вызвавших её сил, тело полностью восстанавливает свою форму и размеры.
Например, если немного согнуть школьную линейку, растянуть пружину или надавить на воздушный шарик, после прекращения действия силы линейка выпрямится, пружина сожмется, и шарик опять станет круглым. Эти деформации – упругие, они обратимы.
Если же приложенная сила окажется слишком большой, линейка сломается, пружина так и останется растянутой, а шарик лопнет. Эти деформации – неупругие, они необратимы.
Все здания и сооружения вокруг нас рассчитываются так, чтобы их «нагруженные» части испытывали только упругие деформации; это обеспечивает надёжность и долговечность конструкций.
Восстановление формы и размера тела при упругой деформации происходит под действием силы упругости, которая возникает благодаря межатомным и межмолекулярным взаимодействиям.
Сила упругости уравновешивает действие внешней силы и направлена в сторону, противоположную смещению частиц.
Например (см. рисунок):
- при растяжении сила упругости стремится сжать тело;
- при сжатии сила упругости стремится распрямить тело.
п.2. Закон Гука
 |
Проведем серию опытов с пружиной. Пусть при действии на пружину силой (F) мы получаем деформацию (удлинение) (Delta l). При этом в пружине возникают силы упругости, стремящиеся вернуть её в исходное положение, (overrightarrow{F_{text{упр}}}=-overrightarrow{F}). Если приложенную силу увеличить в 2 раза, то деформация также увеличится в 2 раза. Увеличение силы в 3 раза приводит к росту деформации в 3 раза и т.д. Опыты показывают, что во всех случаях деформация будет прямо пропорциональна приложенной силе. |
Следовательно, сила упругости также будет прямо пропорциональна деформации: $$ F_{text{упр}}simDelta l $$
Для каждого тела отношение силы упругости к величине деформации при малых упругих деформациях является постоянной величиной $$ k=frac{F_{text{упр}}}{Delta l}=const $$ которая называется коэффициентом упругости или жесткостью.
Жесткость тела зависит от формы, размеров и материала, из которого оно изготовлено.
В системе СИ жесткость измеряется в ньютонах на метр, (frac{text{Н}}{text{м}}).
Закон Гука
Сила упругости, возникающая во время упругой деформации тела, прямо пропорциональна удлинению (величине деформации): $$ F_{text{упр}}=kDelta l $$ Сила упругости всегда направлена противоположно деформации.
п.3. Измерение силы с помощью динамометра
 |
Динамометр– это прибор для измерения силы.
Простейший пружинный динамометр состоит из пружины с крючком и дощечки со шкалой (проградуированной в ньютонах). |
В технике используются динамометры более сложных конструкций.
Но принцип действия – использование закона Гука – во многих из них сохраняется.
п.4. Задачи
Задача 1. Резиновая лента удлинилась на 10 см под действием силы 50 Н. Какова жесткость ленты?
Дано:
(Delta l=10 text{см}=0,1 text{м})
(F=50 text{Н})
__________________
(k-?)
Жесткость ленты $$ k=frac{F}{Delta l} $$ $$ k=frac{50}{0,1}=500 left(frac{text{Н}}{text{м}}right) $$ Ответ: 500 Н/м
Задача 2. Под действием силы 300 Н пружина динамометра удлинилась на 0,6 см. Каким будет удлинение пружины под действием силы 700 Н? Ответ запишите в миллиметрах.
Дано:
(F_1=300 text{Н})
(Delta l_1=0,6 text{см}=6cdot 10^{-3} text{м})
(F_2=700 text{Н})
__________________
(Delta l_2-?)
Жесткость пружины begin{gather*} k=frac{F_1}{Delta l_1}=frac{F_2}{Delta l_2}Rightarrow Delta l_2=frac{F_2}{F_1}Delta l_1\[6pt] Delta l_2=frac{700}{300}cdot 6cdot 10^{-3}=14cdot 10^{-3} (text{м})=14 (text{мм}) end{gather*} Ответ: 14 мм
Задача 3. Пружина без груза имеет длину 30 см и коэффициент жесткости 20 Н/м. Найдите длину растянутой пружины, если на нее действует сила 5 Н. Ответ запишите в сантиметрах.
Дано:
(l_0=30 text{cм}=0,3 text{м})
(k=20 text{Н/м})
(F=5 text{Н})
__________________
(l-?)
Удлинение пружины под действием силы: $$ Delta l=frac Fk $$ Длина растянутой пружины begin{gather*} l=l_0+Delta l=l_0+frac Fk\[6pt] l=0,3+frac{5}{20}=0,3+0,25=0,55 (text{м})=55 (text{cм}) end{gather*} Ответ: 55 cм
Задача 4*. Грузовик взял на буксир легковой автомобиль массой 1,5 т с помощью троса. Двигаясь равноускоренно, они проехали путь 600 м за 50 с. На сколько миллиметров удлинился во время движения трос, если его жесткость равна (3cdot 10^5 text{Н/м})?
Дано:
(m=1,5 text{т}=1500 text{кг})
(s=600 text{м})
(t=50 text{c})
(v_0=0)
(k=3cdot 10^5 text{Н/м})
__________________
(Delta l-?)
Сила упругости, возникающая в тросе, уравновешивает силу тяги, передвигающую автомобиль с постоянным ускорением: $$ F_{text{упр}}=kDelta l=F_{text{т}}=ma $$ Перемещение из состояния покоя $$ s=frac{at^2}{2}Rightarrow a=frac{2s}{t^2} $$ Получаем: begin{gather*} kDelta l=mcdotfrac{2s}{t^2}Rightarrow Delta l=frac mkcdot frac{2s}{t^2}\[6pt] Delta l=frac{1500}{3cdot 10^5}cdot frac{2cdot 600}{50^2}=2,4cdot 10^{-3} (text{м})=2,4 (text{мм}) end{gather*} Ответ: 2,4 мм
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
На сколько сантиметров растянется пружина, жёсткость которой под действием силы 100 H? Пружину считайте идеальной.
2
На рисунке изображен лабораторный динамометр.
Шкала проградуирована в ньютонах. Каким будет растяжение пружины динамометра, если к ней подвесить груз массой 200 г? (Ответ дайте в сантиметрах.) Ускорение свободного падения считать равным 10 м/с2.
3
Под действием силы 4,5 Н пружина удлинилась на 6 см. Чему равен модуль силы, под действием которой удлинение этой пружины составит 4 см? (Ответ дайте в ньютонах.)
5
На сколько растянется пружина жесткостью под действием силы 1000 Н? (Ответ дайте в сантиметрах.)
Пройти тестирование по этим заданиям
На данном уроке мы познакомимся с новым прибором, с помощью которого можно измерить силу, действующую на тело. Как называют прибор для измерения силы?
Динамометр — это прибор для измерения силы.
Слово «динамометр» образовано от двух греческих слов: «динамис» — «сила» и «метрео» — «измеряю».
Рассмотрим самый простой вид динамометра — пружинный. Это поможет нам разобраться с принципом действия прибора. Основной его частью является стальная пружина.
Не сложно догадаться, что если подвесить к пружине груз, то она растянется. Другими словами, наблюдатель видит, что на подвешенное тело действует сила, и может определить ее величину.
Устройство пружинного динамометра
Как изготовить простейший динамометр?
Простой пружинный динамометр можно изготовить самостоятельно (рисунок 1). Он состоит из нескольких частей:
- стальная пружина с крючком и указателем на конце;
- корпус для крепления пружины;
- шкала.
Сначала закрепляем пружину на корпусе таким образом, чтобы ее нижний конец оставался свободным. Затем к нему прикрепляем указатель. Если разогнуть последний виток пружины, то его можно использовать в качестве указателя.
Градуировка шкалы динамометра
Шкалу можно изготовить из полоски обычной бумаги, нанеся на нее штрихи и числа. Поэтому приклеим бумагу на корпус и сделаем на ней первую отметку (рисунок 2, а). Это будет нулевая отметка, которая показывает, где заканчивается нерастянутая пружина.
Из прошлого урока нам известно, что на груз массой $frac{1}{9.8} space кг$ ($102 space г$) будет действовать сила тяжести, равная $1 space Н$. Поэтому подвесим на крючок груз указанной массы и посмотрим, насколько растянется пружина.
Если пружина прекратила растяжение и груз остановился, это означает, что сила тяжести, действующая на тело, и сила упругости пружины уравнялись. Новое положение указателя отметим на бумаге, поставив цифру 1 (рисунок 1, б).
Так мы уже получили начало шкалы и необходимо ее продолжить. И сделать это можно по-разному:
- Поочередно подвешивать грузы массой $204 space г$, $306 space г$, $408 space г$ и т. д., проставляя соответствующие отметки: 2, 3, 4 и т. д.
- Воспользоваться двумя имеющимися отметками (0 и 1) и с помощью линейки отложить отрезки такой же длины, отметив их числами 2, 3, 4 и т. д.
Теперь у нас есть шкала, которая позволяет измерять силу с точностью до целых. Но точность нашей шкалы можно улучшить до десятых, нанеся на нее дополнительные деления — 0.1; 0.2; 0.3; 0.4 и т. д.
Как нанести на шкалу динамометра деления, соответствующие $0.1 space Н$?
Для этого разделим расстояние между отметками 0 и 1 на 10 одинаковых частей, поставив соответствующие штрихи. Аналогично поделим на части и другие отрезки ( между отметками 2 и 3, 3 и 4, и т. д.).
Описанным способом мы осуществили градуировку шкалы, цена деления которой равна $0.1 space Н$.
Принцип действия динамометра
Итак, мы видим, что для измерения силы, действующей на груз, необходимо уравнять ее с силой растяжения пружины динамометра. Указатель, закрепленный на пружине, покажет величину этой силы согласно шкале. Таким образом, можно сделать вывод, что:
Устройство динамометра основывается на сравнении измеряемой силы с силой упругости пружины.
Например, если подвесить груз какой-то массы, то мы будем сравнивать силу тяжести, действующую на этот груз, и величину силы упругости растянутой пружины.
Если мы возьмем крючок на конце пружины и потянем за него, то мы будем сравнивать силу, приложенную нами, с силой упругости пружины (рисунок 3). Так, с помощью динамометра можно измерять различные силы.
Вспомним закон Гука — он гласит, что сила упругости тела при растяжении прямо пропорциональна изменению длины тела. Принцип работы динамометра подтверждает этот закон — пружина удлиняется во столько же раз, во сколько увеличивается сила ее упругости.
Виды динамометров
Какие типы динамометров вам известны?
Можно выделить несколько видов динамометров на основе принципа их действия:
- Механические динамометры (рычажные или пружинные)
В основе работы механических динамометров лежит деформация. Принцип действия пружинного динамометра подробно описан выше. В рычажном динамометре под действием измеряемой силы происходит деформация рычага, которая и показывает величину силы.
- Гидравлические динамометры
Принцип действия таких динамометров основан на определении количества жидкости, вытесняемой из цилиндра под действием измеряемой силы.
- Электрические динамометры
У таких динамометров имеется датчик, который преобразует деформацию в электрический сигнал. Это вид динамометров стал широко применяться в последнее время.
Современные модели динамометров могу соединять и использовать в себе несколько принципов действия.
Применение динамометров
Динамометры имеют очень широкое применение. Например, в медицине используются специальные медицинские динамометры. Они предназначены для измерения силы различных мышечных групп человека.
Одним из таких приборов является ручной динамометр, который называется силомером (рисунок 4). С его помощью измеряется мускульная сила руки при сжатии кисти в кулак.
Для того чтобы измерить тяговые усилия локомотивов, тракторов, морских буксиров и другой техники, используют специальные тяговые динамометры (рисунок 5).
Такие динамометры способны измерять силы до нескольких десятков тысяч ньютонов. Современные модели имеют пульт дистанционного управления с дисплеем (рисунок 6).
При монтаже проводов и кабелей используют динамометры для определения силы натяжения провода (рисунок 7). Существуют специальные монтажные таблицы с необходимыми значениями.
Динамометры используют не только в специальной технике, но и в обычных для нас местах: в метро, в автобусах и даже в лифте. Здесь эти приборы используют для измерения силы сжатия створок различных автоматических дверей.
Упражнения
Упражнение №1
Определите цену деления каждого прибора и силу тяжести, действующую на каждый груз (рисунок 8).
Показать ответ
Скрыть
Определим цену деления динамометра, изображенного на рисунке 8, а. Возьмем два крайних подписанных деления: $1 space Н$ и $0 space Н$. Вычтем меньшее значение из большего и разделим на количество делений между ними:
$frac{1 space Н space − space 0 space Н}{10} = 0.1 space Н$.
Цена деления этого динамометра равна $0.1 space Н$.
На подвешенный груз действует сила тяжести, равная $1 space Н$.
Определим цену деления динамометра, изображенного на рисунке 8, б. Возьмем два крайних подписанных деления: $1 space Н$ и $0 space Н$. Вычтем меньшее значение из большего и разделим на количество делений между ними:
$frac{1 space Н space − space 0 space Н}{2} = 0.5 space Н$.
Цена деления этого динамометра равна $0.5 space Н$.
На подвешенный груз действует сила тяжести, равная $6 space Н$.
Упражнение №2
Чему равен вес каждого груза на рисунке 8? Укажите точку его приложения.
Показать ответ
Скрыть
Груза и динамометры у нас неподвижны, поэтому вес каждого груза будет равен силе тяжести, действующей на него. Значение же силы тяжести мы видим по показаниям динамометров.
Для груза на рисунке 8, а:
$P = F_{тяж} = 1 space Н$.
Для груза на рисунке 8, б:
$P = F_{тяж} = 6 space Н$.
На рисунке 9 изображен вес этих тел. Вес приложен к подвесу в обоих случаях.
Упражнение №3
По рисунку 10 определите, с какой силой растягивается каждая пружина под действием подвешенного к ней груза (масса одного груза $102 space г$).
Дано:
$m = 102 space г$
$g = 10 frac{Н}{кг}$
СИ:
$m = 0.102 space кг$
$F_1 — ?$
$F_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Под действием какой силы будет растягиваться пружина? Она растягивается под влиянием силы тяжести, действующей на подвешенный к ней груз.
Рассчитаем силу, растягивающую причину на рисунке 10, а:
$F_1 = F_{тяж1} = gm$,
$F_1 = 10 frac{Н}{кг} cdot 0.102 space кг = 1.02 space Н$.
Рассчитаем силу, растягивающую причину на рисунке 10, б:
$F_2 = F_{тяж2} = g cdot 2m$,
$F_2 = 10 frac{Н}{кг} cdot 2 cdot 0.102 space кг = 2.04 space Н$.
Ответ: $F_1 = 1.02 space Н$, $F_2 = 2.04 space Н$.