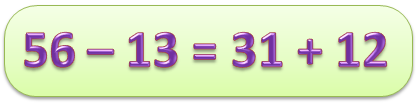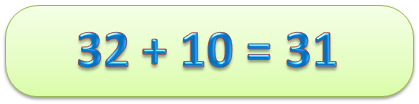На простом примере разберем, что такое «равенство» и «неравенство». Для примера возьмем задания из учебника по математике.
Равенства
Там, где равенства, мы видим «4=4». Здесь все правильно, значит это равенство. Второй пример представлен иначе: слева мы видим «5», а справа от знака «4+1».
Если сложить 4 и 1, то получится 5, и слева стоит 5. Левая и правая часть примера равны, а значит это тоже будет равенством.
Неравенства
В примере из учебника мы видим, что с одной стороны примера стоит «4», а с другой «3». 4 и 3 не равны, а значит это называется «неравенство». В нашем случае между 4 и 3 необходимо поставить знак неравенства «>» – «4>3».
Второй пример в столбике «Неравенства» чуть сложнее. Справа от знака здесь стоит выражение «4-1», а слева просто «4». Если от 4 отнять 1, то получится 3. 3 меньше, чем 4, а значит это также будет неравенство, что и обозначается знаком.
Как не запутаться в знаке неравенства
Для того, чтобы не запутаться в какую сторону ставить знак неравенства, можно представить себе клюв птицы. «Клюв» должен смотреть в сторону того числа, которое меньше. Проще говоря, большее число как бы «клюет» меньшее.
Второй способ – использовать точки. Около большего числа ставятся вертикально две точки, а около меньшего – одна посередине. Затем просто соединяем полученные точки и получаем знак неравенства.
Решаем задания
Задание 1
Давайте разберем несколько заданий на основе того, что мы узнали:
Правильные ответы будут следующие:
4>3 3<4 5>2 3<5 1+2=3 5-3=2
Задание 2
Теперь попробуем найти неверные неравенства:
Правильные ответы будут такими:
4+1=5 – верно
3-1<1 – неверно
4<2 – неверно, правильно будет 4>2
3>4 – неверно, правильно будет 3<4
5-1=3 – неверно, правильно будет 5-1=4
2+1=3 – верно
Задание 3
Здесь нам даны карточки, на которых необходимо поставить правильный знак.
Получаются следующие выражения:
3+1=4
5-1=4
4>3
2<4
5>1
3>2
1<4
5>3
Задание 4
Последнее задание практическое и самое интересное.
Нам нужно ответить на вопросы у кого из ребят больше монет, и у кого больше сумма денег.
Для начала разберемся с количеством монет: у Миши 1 монета, а у Коли 2, значит у Коли монет больше. Запишем это как неравенство: 1<2.
Теперь определим у кого из ребят больше денег. У Миши только одна монета достоинством в 5 рублей. Здесь все просто.
А вот у Коли две монеты в 1 и 2 рубля. Посчитаем сколько всего денег у Коли: 1+2 = 3. Получается, что у Коли 3 рубля.
Теперь мы знаем, что у Миши 5 рублей, а у Коли 3 рубля. Значит денег больше у Миши, чем у Коли. Запишем это как неравенство: 5>2+1.
После получения общих сведений о равенствах в математике переходим к более узким темам. Материал этой статьи даст представление о свойствах числовых равенств.
Что такое числовое равенство
Первый раз мы сталкиваемся с числовыми равенствами еще в начальной школе, когда происходит знакомство с числами и понятием «столько же». Т.е. самые примитивные числовые равенства это: 2=2, 5=5 и т.д. И на том уровне изучения мы называли их просто равенствами, без уточнения «числовые», и закладывали в них количественный или порядковый смысл (который несут натуральные числа). Например, равенство 2=2 будет соответствовать изображению, на котором – два цветка и на каждом сидит по две шмеля. Или, к примеру, две очереди, где вторыми по порядку стоят Вася и Ваня.
По мере появления знаний об арифметических действиях числовые равенства становятся сложнее: 5+7=12; 6-1=5; 2·1=2; 21:7=3 и т.п. Затем начинают встречаться равенства, в записи которых участвуют числовые выражения разного рода. Например, (2+2)+5=2+(5+2); 4·(4−(1+2))+12:4−1=4·1+3−1 и т.п. Дальше мы знакомимся с прочими видами чисел, и числовые равенства приобретают все более и более интересный и разнообразный вид.
Числовое равенство – это равенство, обе части которого состоят из чисел и/или числовых выражений.
Свойства числовых равенств
Сложно переоценить значимость свойств числовых равенств в математике: они являются опорой многому, определяют принцип работы с числовыми равенствами, методы решений, правила работы с формулами и многое другое.Очевидно, что существует необходимость детального изучения свойств числовых равенств.
Свойства числовых равенств абсолютно согласованы с тем, как определяются действия с числами, а также с определением равных чисел через разность: число a равно числу b только в тех случаях, когда разность a−b есть нуль. Далее в описании каждого свойства мы проследим эту связь.
Основные свойства числовых равенств
Изучать свойства числовых равенств начнем с трех базовых свойств, которые присущи всем равенствам. Перечислим основные свойства числовых равенств:
- свойство рефлексивности: a=a;
- свойство симметричности: если a=b, то b=a;
- свойство транзитивности: если a=b и b=c, то a=c,где a, b и c – произвольные числа.
Свойство рефлексивности обозначает факт равенства числа самому себе: к примеру, 6=6, −3=−3, 437=437 и т.п.
Нетрудно продемонстрировать справедливость равенства a−a=0 для любого числа a: разность a−a можно записать как сумму a+(−a), а свойство сложения чисел дает нам возможность утверждать, что любому числу a соответствует единственное противоположное число −a, и сумма их есть нуль.
Согласно свойству симметричности числовых равенств: если число a равно числу b,
то число b равно числу a. К примеру, 43=64, тогда 64=43.
Обосновать данное свойство можно через разность чисел. Условию a=b соответствует равенство a−b=0. Докажем, что b−a=0.
Запишем разность b−a в виде −(a−b), опираясь на правило раскрытия скобок, перед которыми стоит знак минус. Новая запись выражения равна -0, а число, противоположное нулю, это нуль. Таким образом, b−a=0, следовательно: b=a.
Свойство транзитивности числовых равенств гласит, что два числа равны друг другу в случае их одновременного равенства третьему числу. К примеру, если 81=9 и 9=32, то 81=32.
Свойству транзитивности также отвечает определение равных чисел через разность и свойства действий с числами. Равенствам a=b и b=c соответствуют равенства a−b=0 и b−c=0.
Докажем справедливость равенства a−c=0, из чего последует равенство чисел a и c. Посколькусложение числа с нулем не меняет само число, то a−c запишем в виде a+0−c. Вместо нуля подставим сумму противоположных чисел −b и b, тогда крайнее выражение станет таким: a+(−b+b)−c. Выполним группировку слагаемых: (a−b)+(b−c). Разности в скобках равны нулю, тогда и сумма (a−b)+(b−c) есть нуль. Это доказывает, что, когда a−b=0 и b−c=0, верно равенство a−c=0, откуда a=c.
Прочие важные свойства числовых равенств
Основные свойства числовых равенств, рассмотренные выше, являются базисом для ряда дополнительных свойств, довольно ценных в разрезе практики. Перечислим их:
Прибавив к (или убавив от) обеим частям числового равенства, являющегося верным, одно и то же число, получим верное числовое равенство. Запишем буквенно: если a=b, где a и b – некоторые числа, то a+c=b+c при любом c.
В качестве обоснования запишем разность (a+c)−(b+c).
Это выражение легко преобразуется в вид (a−b)+(c−c).
Из a=b по условию следует, что a−b=0 и c−c=0, тогда (a−b)+(c−c)=0+0=0. Это доказывает, что (a+c)−(b+c)=0, следовательно, a+c=b+c;
Если обе части верного числового равенства перемножить с любым числом или разделить на число, не равное нулю, тогда получим верное числовое равенство.
Запишем буквенно: когда a=b, то a·c=b·c при любом числе c. Если c≠0, тогда и a:c=b:c.
Равенство верно: a·c−b·c=(a−b)·c=0·c=0, и из него следует равенство произведений a·c и b·c. А деление на отличное от нуля число c возможно записать как умножение на обратное число 1c;
При a и b, отличных от нуля и равных между собой, обратные им числа также равны.
Запишем: когда a≠0, b≠0 и a=b, то 1a=1b. Крайнее равенство нетрудно доказать: с этой целью разделим обе части равенства a=b на число, равное произведению a·b и не равное нулю.
Укажем еще на пару свойств, которые позволяют осуществлять сложение и умножение соответствующих частей верных числовых равенств:
При почленном сложении верных числовых равенств получается верное равенство. Запись этого свойства такова: если a=b и c=d, то a+c=b+d для любых чисел a, b, c и d.
Обосновать это полезное свойство возможно, опираясь на указанные ранее свойства. Мы знаем, что к обеим частям верного равенства возможно прибавить любое число.
К равенству a=b прибавим число c, а к равенству c=d – число b, итогом станут верные числовые равенства: a+c=b+c и c+b=d+b. Крайнее запишем в виде: b+c=b+d. Из равенств a+c=b+c и b+c=b+d согласно свойству транзитивности следует равенство a+c=b+d. Что и нужно было доказать.
Необходимо уточнить, что почленно можно сложить не только два верных числовых равенства, но и три, и более;
Наконец, опишем такое свойство: почленное перемножение двух верных числовых равенств дает верное равенство. Запишем при помощи букв: если a=b и c=d, то a·c=b·d.
Доказательство этого свойства подобно доказательству предыдущего. Умножим обе части равенства на любое число, умножим a=b на c, а c=d на b, получим верные числовые равенства a·c=b·c и c·b=d·b. Крайнее запишем как b·c=b·d. Свойство транзитивности дает возможность из равенства a·c=b·c и b·c=b·d вывести равенство a·c=b·d, которое нам необходимо было доказать.
И вновь уточним, что данное свойство применимо для двух, трех и более числовых равенств.
Так, можно записать: если a=b, то an=bn для любых чисел a и b, и любого натурального числа n.
Завершим данную статью, собрав для наглядности все рассмотренные свойства:
a=a.
Если a=b, то b=a.
Если a=bи b=c, то a=c.
Если a=b, то a+c=b+c.
Если a=b, то a·c=b·c.
Если a=bи с≠0, то a:c=b:c.
Если a=b, a=b, a≠0 и b≠0, то 1a=1b.
Если a=b и c=d, то a·c=b·d.
Если a=b, то an=bn.
|
Что означают понятия “равенство” и “неравенство” в математике? Приведите примеры. Запись, в которой используется знак “равно” (=), который стоит между математическими объектами, называется “равенством”. Такой знак может разделять два числа, несколько чисел или выражения. Правая и левая части выражений, стоящие перед и после знака “=”, всегда имеют одно и то же значение. Примеры: 5 ∙ 4 = 20; 3 + 6 = 9; 21 : 7 = 3. Бывают случаи, когда выражения имеют совершенно разные значения, в этом случае знак “равно” между ними не ставится. Имеется специальный знак, которым можно отметить, что выражения отличаются между собой: “≠”. Примеры: 15 ≠ 20 – 2; 14 ≠ 6 + 4; 2 ∙ 5 ≠ 12. Неравенство – это понятие, которое связано со сравнением двух математических объектов, но составляются они с использованием знаков “≠”, “>” (больше) и “<“ (меньше). Обычно значения справа и слева от этих знаков имеют разные числовые значения. Примеры: 8 < 10; 3 ∙ 4 > 2 ∙ 5; 81 : 9 < 7 ∙ 8. автор вопроса выбрал этот ответ лучшим Annagne 3 года назад Понятие равенства или неравенства в математике происходит от сравнения либо чисел, либо выражений. Знак равенства обозначается двумя параллельными прямыми одинаковой длины “=”, причём применяться в математике этот знак стал только с конца 16 века, а до этого момента он обозначался в буквенном выражении. Пример равенства : 7=7 или 2+6=8 или a+b=b+a . Неравенство обозначается знаками больше и меньше. Как правило, и само понятие, и знак равенства легко понимается и запоминается, а вот со знаками больше и меньше у многих детей возникают сложности в запоминании и я, в своё время, не была исключением. Помню, как нас учили запоминать эти знаки в советской школе : если подставить птичку к знаку с право и её клювик открыт – значит это знак больше, а если закрыт – то знак меньше. Например : Читаем мы слева на право и данные примеры звучат так :
wildcat 4 года назад Равенство – это когда что-то равно другому. Когда мы имеем по пять пальцев на каждой руке, но два глаза, по одному носу. В математике равенство обозначается двумя короткими параллельными полосками: =. Они означают, что без разницы куда идти и что брать, везде все одинаково. 5=5, 6=6, 7=7. Пять пальцев на одной руке равны пяти пальцам на другой и так было всегда. А вот неравенство, это отсутствие совпадения. Это если у тебя пять пальцев на руке, а у Егора четыре, потому что он был дурак и один палец ему оторвало. Получается, что у тебя пальцев больше: 5>4 Это знак “больше”. Он находится над буквой Ю на клавиатуре и чтобы его извлечь следует использовать английский алфавит. Рядом и знак меньше: <, и тоже доступен он в английской раскладке. 4<5 и это действительно так. Попробуйте поднять четыре килограмма, а потом возьмите пять. Чувствуете разницу? Author 5 лет назад Для данного употребляется знак равно (и ещё его именуют знаком равенства), какой имеет вид =. Пример При записи различных равенств вносят равные объекты, а также между ними и ставят знак =. К примеру сказать, запись равных чисел 6 и 6 будет начертано следующим образом 6=6, и ее можно прочесть как «шесть равно шести» А если письменно нам потребуется отметить неравенство 2 объектов, тогда применяется знак не равно ≠. Знак представляет собой просто перечеркнутый знак равно. Например, запись 3+5≠7. Можно прочесть так: «Сумма тройки и пятерки не равна семи». Еще используются знаки “<“, “>”. Меньше, больше. Когда мы говорим про числовое равенство, мы используем знак “=”. При этом одно числовое выражение, которые стоит справа, равно числовому выражению, которое находится слева. Числовые равенства обладают несколькими свойствами:
Также, если мы проделываем с обоими частями равенства некие одинаковые манипуляции, то равенство не меняет. Например, умножение, сложение (кроме манипуляций с 0), деление и вычитание.
Когда мы говорим про числовые неравенства, то подразумеваем, что она часть выражения больше или меньше другой. Тогда знак равенства не используется, берутся знаки “<” или “>”, “≤” или “≥”. Они также обладают рядом свойств. И могут быть верными и неверными. Например: 3+5>6 – это верное неравенство; 3+5<6 – это неверное неравенство. Равенство или неравенство – вытекает из сравнения чисел или выражений. Что то одинаковое при сравнении можно назвать равенством. Например 2+5 будет 7 и 3+4 даст в сумме 7 эти два выражения 2+5 и 3+4 между собой равны и записать можно так: 2+5=3+4 Неравенством, соответственно будет выражение, в котором сумма в правой части будет отличаться от суммы в левой части выражения. Например: 2+6 не равно 3+4, а больше по значению. Неравенство записывают знаками больше или меньше или перечеркнутым знаком равенства. Maria Muzja 5 лет назад Эти понятия (равенство/неравенство) в математике, очень взаимосвязаны между собой. Равенство – это понятие, которое проходят еще в начальной школе, и под этим термином, надо понимать “высказывание”, к которому можно применить знак “=”, что-то равное и идентичное. Бывают и числовые равенства. Бываеют равенства неверные и верные. А “неравенство” – это такое математическое утверждение, показывающее, на сколько одно число, отличается от другого. Dilyara K 5 лет назад Равенством называют такие математические выражения, когда значения слева и справа от знака “=” равны. Равенство, примеры: 18 – 6*2 = 6 23 – (13 + 3) = 7 Если значения слева и справа различны, то вместо знака равенства ставятся знаки неравенства “<“, “>”, в зависимости от того, какая сторона неравенства больше. Неравенство, примеры: 7 – 9 < 5 17 > 21 – 19 [пользователь заблокирован] 5 лет назад В алгебре существует понятие “математическое выражение”. Если совсем просто это, набор всевозможных математических действий и преобразований. Результатом “выражения” является его значение. Если значения двух выражений одинаковы, значит присутствует “равенство”, если значения отличаются, это “неравенство” Алиса в Стране 4 года назад Равенство в математике – это математическое выражение, между частями которого стоит знак “ровно”. Например: 7 + 5 = 12 lg (x + 3) = 3 + 2 lg 5 Неравенство же это когда в математическом выражении между его частями стоит не знак “равно”, а знак “меньше” или знак “больше”. Например: 4 – 2 < 5 4 (х – 2)∙(х + 2) > 0. Иногда между частями выражения ставится вот такой вот знак (перечеркнутый знак “равно”: ≠, тогда это выражение тоже можно назвать неравенством: 20 + 5 ≠ 19 √ n(х) ≠ √ m(х) isa-isa 4 года назад “Равенством” в математике называются примеры, в которых между числами или произведениями чисел стоит знак “равно” =. Например: 2х2=4, либо 2х2=1+3, это верное равенство. Бывают неверные равенства, когда пример решен неверно. Неравенство, это когда между числами стоят знаки больше или меньше. Как же как и равенства, неравенства бывают неверными. 31-26 < 7 2х2 < 5 100 > 68-7 Знаете ответ? |
В данной публикации мы рассмотрим, что такое арифметическое (математическое) равенство, а также перечислим его основные свойства с примерами.
- Определение равенства
-
Свойства равенств
- Свойство 1
- Свойство 2
- Свойство 3
Определение равенства
Математическое выражение, которое содержит числа (и/или буквы) и знак “равно”, разделяющий его на две части, называется арифметическим равенством.
Выделяют 2 типа равенств:
- Тождество – обе части тождественно равны. Например:
- 5 + 12 = 13 + 4
- 3x + 9 = 3 ⋅ (x + 3)
- Уравнение – равенство верно при определенных значениях содержащихся в нем букв. Например:
- 10x + 20 = 43 + 37
- 15x + 10 = 65 + 5
Свойства равенств
Свойство 1
Части равенства можно менять местами, при этом оно останется верным.
Например, если:
12x + 36 = 24 + 8x
Следовательно:
24 + 8x = 12x + 36
Свойство 2
К обеим частям равенства можно прибавить или отнять одно и то же число (или математическое выражение). Равенство при этом не будет нарушено.
То есть, если:
a = b
Значит:
- a + x = b + x
- a – y = b – y
Примеры:
- 16 – 4 = 10 + 2 ⇒ 16 – 4 + 5 = 10 + 2 + 5
- 13x + 30 = 7x + 6x + 30 ⇒ 13x + 30 – y = 7x + 6x + 30 – y
Свойство 3
Если обе части равенства умножить или разделить на одно и то же число (или математическое выражение), оно не будет нарушено.
То есть, если:
a = b
Значит:
- a ⋅ x = b ⋅ x
- a : y = b : y
Примеры:
- 29 + 11 = 32 + 8 ⇒ (29 + 11) ⋅ 3 = (32 + 8) ⋅ 3
- 23x + 46 = 20 – 2 ⇒ (23x + 46) : y = (20 – 2) : y
Числовые равенства
Чтобы получить запись, называемую числовым равенством, надо два числовых выражения соединить знаком равенства (=).
Пример:
Представленный пример является верным числовым равенством, но числовое равенство может быть неверным:
Давайте разберем свойства числовых равенств.
- Если числовое равенство верно, то прибавив к обеим частям этого равенства одно и тоже число мы получим верное числовое равенство.
Например:
Проверим равенство
(12 + 3) = (9 + 6)
12 + 3 = 15 и 9 + 6 = 15
Равенство верно, теперь проверим свойство
(12 + 3) + (5 – 2) = (9 + 6) + (5 – 2)
15 + (5 – 2) = 15 + (5 – 2)
18 = 18
В обоих случаях равенства верны
То же самое произойдет, если мы вычтем одно и то же числовое выражение из обеих частей верного числового равенства.
Проверим это свойство на предыдущем примере заменив действие сложение на вычитание:
(12 + 3) – (5 – 2) = (9 + 6) – (5 – 2)
15 + (5 – 2) = 15 + (5 – 2)
12 = 12
Как мы видим равенство верно.
- Если числовое равенство верно, то умножив обе части этого равенства на одно и тоже числовое выражение мы получим верное числовое равенство.
Проверим и это свойство:
(75 – 3) = (15 + 57)
75 – 3 = 72 и 15 + 57 = 72 это равенство верно
(75 – 3) · (10 – 2) = (15 + 57) · (10 – 2)
72 · (10 – 2) = 72 · 8 = 576
576 = 576
Свойство доказано.
- Если числовое равенство верно, то разделив обе части этого равенства на одно и тоже числовое выражение мы получим верное числовое равенство. Правда, это выражение справедливо только если числовое выражение не равно нулю, так как на ноль делить нельзя.
Проверим это свойство:
(12 + 3) : (5 – 2) = (9 + 6) : (5 – 2)
15 : 3 = 15 : 3
5 = 5
Что и требовалось доказать.
Числовые неравенства
Если одно числовое выражение не равно другому, то сравним оба выражения поставим между ними знак сравнения – больше (>) или меньше (<). Мы получим числовое неравенство.
(3 · 4) < (3 · 6)
(10 + 25)
Числовые неравенства также могут быть верными и неверными:
(25 – 5) : 5 > 10 – это неравенство неверно
(25 – 5) : 5 < 10 – это неравенство верно
Спасибо, что Вы с нами!
Понравилась статья – поделитесь с друзьями:
Оставляйте пожалуйста комментарии в форме ниже