Как найти равенство квадрата

Равенство окружностей

Первый признак равенства окружностей

Формулировка первого признака равенства окружностей:

Если диаметр одной окружности равен диаметру другой окружности,
то такие окружности равны.

Доказательство первого признака равенства окружностей:

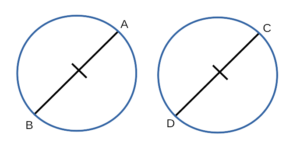
1. Рассмотрим окружность с диаметром BA и окружность с диаметром DC, в которых BA = DC. Докажем,
   что окружность с диаметром BA и окружность с диаметром DC равны.
2. BA = DC, значит окружность с диаметром BA можно наложить на окружность с диаметром DC так, что они совместятся:
   окружность с диаметром BA совместится с окружностью с диаметром DC.
3. Итак, окружность с диаметром BA и окружность с диаметром DC полностью совместятся, значит они равны — ч.т.д

Второй признак равенства окружностей

Формулировка второго признака равенства окружностей:

Если радиус одной окружности соответственно равен радиусу другой окружности, то такие окружности равны.

Доказательство второго признака равенства окружностей:

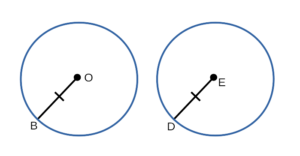
1. Рассмотрим окружность с радиусом BO и окружность с радиусом DE, в которых BO = DE. Докажем,
   что окружность с радиусом BO и окружность с радиусом DE равны.
2. BO = DE, значит окружность с радиусом BO можно наложить на окружность с радиусом DE так, что они совместятся:
   окружность с радиусом BO совместится с окружностью с радиусом DE.
3. Итак, окружность с радиусом BO и окружность с радиусом DE полностью совместятся, значит они равны — ч.т.д.

Третий признак равенства окружностей

Формулировка третьего признака равенства окружностей:

Если луч делит угол между центрами двух окружностей на два равных угла, то такие окружности равны.

Доказательство третьего признака равенства окружностей:

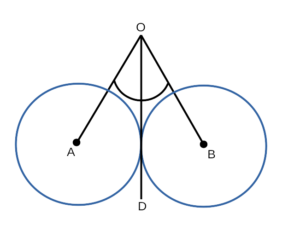
1. Рассмотрим луч OD, окружность с центром в точке A и окружность с центром в точке В, отрезки OA и OB, в которых ∠AOD = ∠BOD. Докажем,что окружность с центром в точке A и окружность с центром в точке B равны.
   
2. ∠AOD = ∠BOD, значит отрезки OA и OB можно наложить друг на другу так, что они совместятся:
   отрезок OA совместится с отрезком OB.
   
3. Итак, окружность с центром в точке A и окружность с центром в точке B полностью совместятся, значит они равны — ч.т.д.

Равенство окружностей можно доказать с помощью трех признаков:

1. По диаметру.
2. По радиусу.
3. По лучу и углу.

Квадрат. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):

Можно дать и другие определение квадрата.

Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.

Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).

Свойства квадрата

• Длины всех сторон квадрата равны.
• Все углы квадрата прямые.
• Диагонали квадрата равны.
• Диагонали пересекаются под прямым углом.
• Диагонали квадрата являются биссектрисами углов.
• Диагонали квадрата точкой пересечения делятся пополам.

Изложеннные свойства изображены на рисунках ниже:

Диагональ квадрата

Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

.

(1)

Из равенства (1) найдем d:

.

(2)

Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.

Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:

Ответ:

Окружность, вписанная в квадрат

Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):

Формула вычисления радиуса вписанной окружности через сторону квадрата

Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:

(3)

Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.

Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:

Ответ:

Формула вычисления сторон квадрата через радиус вписанной окружности

Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:

(4)

Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.

Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:

Ответ:

Окружность, описанная около квадрата

Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):

Формула радиуса окружности описанной вокруг квадрата

Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.

Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:

(5)

Из формулы (5) найдем R:

(6)

или, умножая числитель и знаменатель на , получим:

.

(7)

Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.

Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:

Ответ:

Формула стороны квадрата через радиус описанной около квадрата окружности

Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.

Из формулы (1) выразим a через R:

.

(8)

Пример 5. Радиус описанной вокруг квадрата окружности равен Найти сторону квадрата.

Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя в (8), получим:

Ответ:

Периметр квадрата

Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:

(9)

где − сторона квадрата.

Пример 6. Сторона квадрата равен . Найти периметр квадрата.

Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя в (9), получим:

Ответ:

Признаки квадрата

Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.

Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.

Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).

Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть

(10)

Так как AD и BC перпендикулярны, то

Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда

(12)

Эти реугольники также равнобедренные. Тогда

Из (13) следует, что

(14)

Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).

Квадрат

Квадрат – ромб, у которого все углы прямые.

Квадрат – прямоугольник с равными сторонами.

Квадрат – параллелограмм, у которого все стороны равны и все углы равны.

Свойства квадрата

Все свойства параллелограмма, ромба, прямоугольника верны для квадрата.

Признаки квадрата

Четырехугольник будет являться квадратом, если выполняется хотя бы одно из условий:

1. Все стороны равны и среди внутренних углов есть прямой угол.

2. Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.

3. Четырехугольник обладает поворотной симметрией: он не изменится при повороте на 90˚.

Описанная окружность

Около квадрата можно описать окружность. Сторона и радиус окружности связаны соотношением:

Вписанная окружность

В квадрат можно вписать окружность. Радиус вписанной окружности и сторона квадрата связаны соотношением:

Площадь квадрата

Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

[spoiler title=”источники:”]

http://matworld.ru/geometry/kvadrat.php

[/spoiler]

Решение квадратных уравнений

6 июля 2011

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

Квадратное уравнение — это уравнение вида ax² + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

1. Не имеют корней;
2. Имеют ровно один корень;
3. Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант.

Дискриминант

Пусть дано квадратное уравнение ax² + bx + c = 0. Тогда дискриминант — это просто число D = b² − 4ac.

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

1. Если D < 0, корней нет;
2. Если D = 0, есть ровно один корень;
3. Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:

1. x² − 8x + 12 = 0;
2. 5x² + 3x + 7 = 0;
3. x² − 6x + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8)² − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3² − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6)² − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D < 0, корней нет — ничего считать не надо.

Задача. Решить квадратные уравнения:

1. x² − 2x − 3 = 0;
2. 15 − 2x − x² = 0;
3. x² + 12x + 36 = 0.

Первое уравнение:
x² − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2)² − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x − x² = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2)² − 4 · (−1) · 15 = 64.

D > 0 ⇒ уравнение снова имеет два корня. Найдем их

[begin{align} & {{x}_{1}}=frac{2+sqrt{64}}{2cdot left( -1 right)}=-5; \ & {{x}_{2}}=frac{2-sqrt{64}}{2cdot left( -1 right)}=3. \ end{align}]

Наконец, третье уравнение:
x² + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12² − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

[x=frac{-12+sqrt{0}}{2cdot 1}=-6]

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

1. x² + 9x = 0;
2. x² − 16 = 0.

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Уравнение ax² + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax² = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.

Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax² + c = 0. Немного преобразуем его:

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c/a) ≥ 0. Вывод:

1. Если в неполном квадратном уравнении вида ax² + c = 0 выполнено неравенство (−c/a) ≥ 0, корней будет два. Формула дана выше;
2. Если же (−c/a) < 0, корней нет.

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c/a) ≥ 0. Достаточно выразить величину x² и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax² + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

Задача. Решить квадратные уравнения:

1. x² − 7x = 0;
2. 5x² + 30 = 0;
3. 4x² − 9 = 0.

x² − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x₁ = 0; x₂ = −(−7)/1 = 7.

5x² + 30 = 0 ⇒ 5x² = −30 ⇒ x² = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x² − 9 = 0 ⇒ 4x² = 9 ⇒ x² = 9/4 ⇒ x₁ = 3/2 = 1,5; x₂ = −1,5.

Смотрите также:

1. Теорема Виета
2. Следствия из теоремы Виета
3. Тест на тему «Значащая часть числа»
4. Метод коэффициентов, часть 1
5. Однородные тригонометрические уравнения: общая схема решения
6. Задача B4: строительные бригады

Самой простой формула расчета площади квадрата (S) будет в том случае, если известна длина стороны (a) этой фигуры – просто умножьте ее на саму себя (возведите в квадрат) : S = a².
2
Если в условиях задачи дана длина периметра (P) этой фигуры, к приведенной выше формуле надо добавить еще одно математическое действие. Так как периметр складывается из суммы длин всех сторон многоугольника, в квадрате он содержит четыре одинаковых слагаемых, т. е. длину каждой стороны можно записать как P/4. Подставьте это значение в формулу предыдущего шага. У вас должно получиться такое равенство: S = P²/4² = P²/16.
3
Диагональ квадрата (L) соединяет две его противоположных вершины, образуя вместе с двумя сторонами прямоугольный треугольник. Это свойство фигуры позволяет с использованием теоремы Пифагора (L²=a²+a²) по длине диагонали вычислить длину стороны (a=L/√2). Подставьте и это выражение во все ту же формулу из первого шага. В общем виде решение должно выглядеть так: S = (L/√2)² = L²/2.
4
Можно рассчитать площадь квадрата и по диаметру (D) описанной около него окружности. Так как диагональ любого правильного многоугольника совпадает с диаметром описанной окружности, в формуле предыдущего шага замените лишь обозначение диагонали обозначением диаметра: S = D²/2. Если нужно выразить площадь не через диаметр, а через радиус (R), преобразуйте равенство таким образом: S = (2*R)²/2 = 2*R².
5
Вычисление площади по диаметру (d) вписанной окружности немногим сложнее, так как применительно к квадрату эта величина всегда равна длине его стороны. Как и в предыдущем шаге, для получения формулы вычислений вам нужно лишь заменить обозначение в уже описанном выше равенстве – на этот раз задействуйте тождество из первого шага: S = d². При необходимости использовать вместо диаметра радиус (r), трансформируйте эту формулу так: S = (2*r)² = 4*r².

План урока:

Определение квадратного уравнения

Решение квадратного уравнения

Уравнения, сводящиеся к квадратным

Задачи, решаемые с помощью квадратных уравнений

Теорема Виета

Разложение квадратного трехчлена на множители

Дробно-рациональные уравнения

Определение квадратного уравнения

Изучая понятие многочленов, мы познакомились с квадратными трехчленами. Так называют полином 2-ой степени, содержащий только одну переменную. Если его приравнять к нулю, то получится квадратное уравнение. Дадим определение квадратному уравнению:

Приведем несколько конкретных примеров:

• 5х² + 4х + 7 = 0
• – 3х² + х – 1,5 = 0
• 0,05х² + 99,568х – 47,21 = 0

Числа a, b и с называют коэффициентами квадратного уравнения. Отметим, что числа b и c могут равняться нулю, и в этом случае соответствующее слагаемое просто не записывается:

• 9х² + 5х = 0
• 17х² – 34 = 0

Эти уравнения именуют неполными.

Если же коэффициент а=0, то получается линейное уравнение, которое мы уже умеем решать:

• 6х – 2 = 0
• 67х + 89 = 0

Естественно, что для обозначения переменной может использоваться любая буква, а не только х:

• у² + 3,5х – 93 = 0
• – 32z² + 11z – 78 = 0

Для обозначения коэффициентов могут использоваться специальные термины:

• а – старший коэффициент;
• b– второй коэффициент;
• с – свободный член.

Неполные квадратные уравнения можно очень легко решить. Сначала рассмотрим пример, в котором b = 0:

5х² – 45 = 0

Перенесем вправо свободный коэффициент:

5х² = 45

Далее поделим на старший коэффициент обе части равенства:

х² = 9

Понятно, что х равен квадратному корню из 9. Напомним, что у каждого положительного числа есть два квадратных корня! Один из них является положительным числом и называется арифметическим, а другой противоположен ему по знаку. Поэтому можно записать, что

Иногда используют более короткую запись:

х = ± 3

Не любое квадратное уравнение, у которого нет второго коэффициента b, будет иметь решение. Рассмотрим уравнение

3х² + 75 = 0

Будем решать его таким же путем, перенося свободный коэффициент c вправо и деля уравнение на старший коэффициент a:

3х² + 75 = 0

3х² = – 75

х² = – 25

Квадрат действительного числа не может быть отрицательным. Значит, данное уравнение не будет иметь корней.

Сформулируем общий алгоритм решения неполных квадратных уравнений такого типа:

Теперь изучим неполные уравнения, в которых нет свободного слагаемого с. Рассмотрим их на примере:

7х² + 21х = 0

Слева вынесем переменную х за скобки:

х(7х + 21) = 0

Теперь слева находится произведение двух множителей, а справа – ноль. Очевидно, что произведение может равняться нулю лишь в том случае, когда один из составляющих его множителей (х или 7х + 21) является нулем.

Зная это, запишем:

х = 0 или 7х + 21 = 0

Получили корень х = 0 и ещё одно линейное уравнение, которое легко решить:

7х + 21 = 0

7х = – 21

х = – 3

В результате имеем два корня: 0 и – 3

Опишем общий алгоритм решения этих неполных уравнений:

Решение квадратного уравнения

Найти решение квадратного уравнения, если оно полное, достаточно тяжело. Нам поможет формула квадрата суммы:

(а + b)² = a² + 2ab + b²

Напомним, что с ее помощью можно разложить на множители некоторые квадратные полиномы:

х² + 8х + 16 = х² + 2•4•х + 4² = (х + 4)²

Конечно, здесь нам повезло с квадратным трехчленом – его коэффициенты позволяли воспользоваться формулой квадрата суммы. Однако похожие преобразования можно выполнить и тогда, когда коэффициенты не такие удобные:

х² + 8х + 20 = х² + 8х + 16 + 4 =(х² + 8х + 16) + 4 = (х² + 2•4•х + 4²) + 4 =

= (х + 4)² + 4

Здесь мы разложили число 20 на сумму 16 + 4, чтобы можно было часть выражения «свернуть» формулой квадрата суммы. Такой прием можно применить вообще к любому квадратному трехчлену:

4х² + 10х + 4 = (2х)² + 2•2х•2,5 + 2,5² – 2,5² + 4 = (2х + 2,5)² – 2,5² + 4 =

= (2х + 2,5)² – 6,25 + 4 = (2х + 2,5)² – 2,25

Здесь мы добавили к трехчлену слагаемое 2,5² и тут же его отняли. Оно было необходимо для получения формулы квадрата суммы.

Отметим, что подобное свертывание можно использовать для решения квадратного уравнения. Действительно, пусть дано уравнение

4х² + 10х + 4 = 0

Выше мы уже преобразовали трехчлен, стоящий слева. Произведем замену:

(2х + 2,5)² – 2,25 = 0

Имеем уравнение, очень похожее на неполное, где отсутствует коэффициент b. Попробуем его решить аналогичным путем:

Из этой записи мы получили два линейных уравнения:

2х + 2,5 = – 1,5 или 2х + 2,5 = 1,5

Решая их, находим два корня:

2х = – 1,5 – 2,5 или 2х = 1,5 – 2,5

2х = – 4 или 2х = – 1

х = – 2 или х = – 0,5

Аналогично можно решить и любое другое полное квадратное уравнение. Однако проще пользоваться специальными формулами, в которые надо подставлять значения коэффициентов a, b, с и получать корни квадратного уравнения. Выведем эти формулы.

Пусть есть уравнение

ах² + bх + с = 0

Поделим обе части уравнения на коэффициент а:

Далее надо выделить квадрат суммы, что бы потом свернуть его по формуле сокращенного умножения:

Далее обозначим числитель в правой части (b² – 4ac) буквой D. Эту величину называют дискриминантом квадратного уравнения.

Перепишем уравнение с учетом этой замены:

Далее рассмотрим три случая:

1. D< 0. Если D отрицателен, то и вся дробь справа меньше нуля (так как в знаменателе стоит 4а² – заведомо положительное число). Слева стоит квадрат выражения, а он никак не может оказаться отрицательным. В итоге имеем, что при отрицательном дискриминанте у уравнения отсутствуют корни.
2. D = 0. При таком варианте справа получается ноль:

Квадрат только одного числа равен нулю – самого нуля, поэтому

Итак, при нулевом дискриминанте у уравнения есть только один корень.

1. D> 0. В этом варианте дробь справа оказывается положительным числом, а потому у нее есть два квадратных корня. Решение будет выглядеть так:

Полученное выражение называют основной формулой корней квадратного уравнения.

Если дискриминант – положительное число, то уравнение существует два корня. Для вычисления первого из них надо в формуле квадратного уравнения вместо знака ± поставить минус, а для вычисления второго – знак плюс. Часто 1-ый корень обозначают как х₁, а 2-ой – как х₂. Заметим, что если D = 0, то при подстановке в основную формулу будет получаться один и тот же корень независимо от выбора знака плюс или минус.

Пример. Решите уравнение

2х² – 5х – 3 = 0

Решение. Выпишем коэффициенты уравнения

a = 2

b = – 5

c = – 3

Вычислим значение дискриминанта:

D = b² – 4ас = (– 5)² – 4•2•(– 3) = 25 + 24 = 49

Так как он больше нуля, то должно получиться два корня. Их можно найти по основной формуле квадратного уравнения:

Ответ: – 0,5; 3

Пример. Найдите все корни уравнения

3х² + 6х + 5 = 0

Решение. Найдем дискриминант:

D = b² – 4ас = 6² – 4•3•5 = 36 – 60 = – 24

Дискриминант оказался отрицательным, значит, и корней у уравнения нет.

Ответ: нет корней.

Пример. Найдите значения х, при которых выполняется равенство

4х² – 12х + 9 = 0

Решение. Вычислим дискриминант:

D = (– 12)² – 4•4•9 = 144 – 144 = 0

Так как D = 0, существует лишь один корень:

Ответ: 1,5

Пример. Найдите значения у, при которых справедливо равенство

2у² + 4у + 9 = у² + 11у + 3

Решение. На первый взгляд это уравнение не похоже на изучавшие до этого квадратные уравнения. Однако слагаемые, записанные справа, можно перенести влево, после чего можно будет привести подобные слагаемые:

2у² + 4у + 9 = у² + 11у + 3

2у² + 4у+ 9–у²– 11у– 3 = 0

у² – 7у + 6 = 0

Получили классическое квадратное уравнение, для которого можно рассчитать дискриминант:
D = b² – 4ас = (– 7)² – 4•1•6 = 49 – 24 = 25

Найдем значения двух корней:

Ответ: 1; 6

Уравнения, сводящиеся к квадратным

Так как любое квадратное уравнение решается довольно легко, то другие, более сложные уравнения, часто пытаются свести к квадратным. Сначала рассмотрим так называемые биквадратные уравнения. Пусть надо решить уравнение

2х⁴–26х² + 72 = 0

На первый взгляд в левой части стоит полином четвертой, а не второй степени, то есть это уравнение не является квадратным. Введем переменную t, равную х²:

t = х²

Если это выражение возвести в квадрат, то получим

t² = (х²)² = х⁴

Теперь заменим в исходном уравнении х⁴ на t², а х² на t:

2t²–26t + 72 = 0

Получили квадратное уравнение, из которого можно найти значение t. Посчитаем дискриминант:

D = (– 26)²– 4•2•72 = 676 – 576 = 100

Можно найти два значения t:

Однако нам надо найти значение х, а не t. Вспомним, что мы проводили замену

х² = t

Подставляя вместо t найденные корни 4 и 9, получим ещё два уравнения:

х² = 4

х² = 9

Первое имеет корни (– 2) и 2, а второе (– 3) и 3. Все эти 4 числа являются корнями исходного уравнения

2х⁴ – 26х² + 72 = 0

Уравнения, которые можно свести к квадратному заменой переменных t = x², называют биквадратными уравнениями.

Мы рассмотрели пример, в котором биквадратное уравнение имело 4 корня. Однако порою их может быть и меньше.

Пример. Укажите все корни уравнения

у⁴ + 4у² – 5 = 0

Решение. Данное уравнение подходит под определение биквадратного, а потому произведем замену t = y²:

t² + 4t – 5 = 0

Решаем его:

D = 4²– 4•1•(– 5) = 16 – (– 20) = 36

далее проводим обратную замену и получаем уравнения:

у² = – 5

у² = 1

Первое из них не имеет решения, ведь квадрат числа – это неотрицательное число. Поэтому решать придется только второе уравнение:

у² = 1

у = –1 и у = 1

Ответ –1 и 1.

Подстановка t = x² самая простая и очевидная, однако, порою нужно выполнять более сложные подстановки.

Пример. Найдите все z, для которых выполняется условие

(z – 2)(z – 3)(z – 4)(z – 5) = 24

Решение.Замена неочевидна, и всё же попробуем такой вариант:

t = z– 3,5

Тогда содержимое каждой скобки примет вид:

z– 2 = z– 3,5 + 1,5 = t + 1,5

z– 3 = z– 3,5 + 0,5 = t + 0,5

z– 4 = z– 3,5 – 0,5 = t–0,5

z– 5 = z – 3,5 – 1,5 = t–1,5

Уравнение примет вид:

(t + 1,5)(t + 0,5)(t – 0,5)(t – 1,5) = 24

Поменяем местами скобки:

(t – 0,5)(t + 0,5)(t – 1,5)(t + 1,5) = 24

Можно заметить, что в соседние скобки можно переписать, используя формулу разности квадратов:

(t²– 0,5²)(t²– 1,5²) = 24

Для удобства произведем ещё одну замену s = t²:

(s– 0,5²)(s– 1,5²) = 24

(s– 0,25)(s– 2,25) = 24

Раскроем скобки в левой части:

s²– 2,25s– 0,25s + 0,5625 = 24

s²– 2,5s + 0,5625– 24 = 0

s²– 2,5s– 23,4375 = 0

Получили классическое квадратное уравнение, которое решается через дискриминант:

D = (– 2,5)² – 4•1•(– 23,4375) = 6,25 + 93,75 = 100

Произведем 1-ую обратную замену t² = s:

t² = – 3,75

t² = 6,25

Первое уравнение решений не имеет, а у второго ровно 2 корня:

Пришло время второй замены z– 3,5 = t, из которой получаем два уравнения:

z– 3,5 = – 2,5 или z– 3,5 = 2,5

z= – 2,5 + 3,5 или z= 2,5 + 3,5

z = – 1 или z = 6

Ответ: – 1 и 6.

Задачи, решаемые с помощью квадратных уравнений

При рассмотрении задач, связанных с геометрией, свойствами чисел, движением тел, очень часто возникают квадратные уравнения.

Пример. Площадь прямоугольника составляет 126 см², а одна из его сторон на 5 см длиннее другой. Каковы длины сторон этого прямоугольника?

Решение. Обозначим как k длину той стороны прямоугольника, которая меньше. Тогда протяженность второй стороны будет равна k + 5 см. Площадь прямоугольника – это произведение его сторон, а потому можно записать:

k(k + 5) = 126

Решим это уравнение:

k(k + 5) – 126 = 0

k² + 5k – 126 = 0

D = 5²– 4•1•(– 126) = 25 + 504 = 529

Первый корень равен (– 14). Однако ясно, что длина стороны прямоугольника не может измеряться отрицательным числом, поэтому этот корень надо отбросить. Остается только k = 9. То есть длина первой стороны равна 9 см. Вторая сторона равна k + 5, то есть 9 + 5 = 14 см.

Ответ: 9 и 14 см.

Пример. Сумма квадратов двух последовательных нечетных чисел составляет 290. Что это за числа?

Решение. Обозначим первое число как n. Нечетные числа чередуются с четными, поэтому следующим нечетным числом будет n + 2. Перепишем условие задачи в виде уравнения и найдем его корни:

n² + (n + 2)² = 290

n² + n² + 4n + 4 – 290 = 0

2n² + 4n – 286 = 0

D = 4²– 4•2•(– 286) = 16 + 2288 = 2304

Получили два решения. Если первое число равно – 13, то второе составит n + 2 = – 11. Если же n = 11, то второе число будет равно 13.

Ответ: – 13 и 11, либо 11 и 13.

Теорема Виета

Большое значения имеют уравнения, у которых старшим коэффициентом является единица. Математики называют их приведенными уравнениями.

Дадим несколько примеров приведенных квадратных уравнений:

• х² + 6х + 29 = 0
• у² – 7,54у + 87 = 0
• z² + 21z + 112 = 0

Название «приведенное» возникло из-за того, что каждое квадратное уравнение можно сделать приведенным, если поделить его части на коэффициент перед х². Пусть есть уравнение

4х² + 5х + 6 = 0

Поделим на 4 обе его части:

х² + 1,25х + 1,5 = 0

Для приведенного уравнения сформулирована теорема Виета, которая указывает на взаимосвязь его корней и коэффициентов:

Доказать это очень легко. Если у уравнения

х² + px + q = 0

существует два корня, то они вычисляются по формулам:

Найдем их сумму:

Аналогично можно посчитать и их произведение:

Естественно, если у уравнения не существует корней (D< 0), то теорема к нему неприменима. Если же корень есть ровно один корень, тогда надо считать, что у уравнения два одинаковых корня.

Удостоверимся в верности этой теоремы на примерах.

1. х²– 8х + 15 = 0; корни (х₁ и х₂) равны 3 и 5, в чем можно убедиться подстановкой:

3² – 8•3 + 15 = 0

5² – 8•5 + 15 = 0

Перемножим корни и получим 3•5 = 15 (свободный член), при сложении корней получается 3 + 5 = 8 (второй коэффициент без минуса);

1. у² + 13у + 42= 0, корни (– 6) и (– 7), произведение корней 42, сумма корней – 13;
2. х² + 2х – 8 = 0, корни (– 4) и 2, их сумма равна (– 2), а произведение (– 8).

Справедливо и утверждение, известное как обратная теорема Виета:

Возьмем числа 4 и 9. Их сумма равна 13, а произведение 36, поэтому они являются корнями уравнения:

х² – 13х + 36 = 0

в чем можно убедиться, подставив их вместо х.

Пример. Учитель математики перед уроком составляет квадратные уравнения, причем стремится к тому, чтобы у них были целые корни (чтобы детям было просто считать). Подскажите ему пример уравнения, чьи корни равны 3 и 8.

Решение. Перемножим и сложим числа 3 и 8:

3•8 = 24

3 + 8 = 11

Соответственно, уравнением с корнями 3 и 8 будет

х² – 11х + 24 = 0

Ответ: х² – 11х + 24 = 0

Разложение квадратного трехчлена на множители

При решении уравнения

ах² + bх + с = 0

мы находим его корни. Однако отдельно выделяют и такое понятие, как корень многочлена. Так называют значение переменной, которая обращает полином в ноль.

Понятно, что для нахождения корней полинома второй степени следует решить квадратное уравнение.

Сначала рассмотрим трехчлены, у которых коэффициент при х²а равен 1. Предположим, что нам удалось разложить его на произведение двух линейных полиномов:

х² + bх + с = (х –s)(х –k)

где s и k– какие-то произвольные числа.

Выражение справа является произведением, а потому обращается в ноль только тогда, когда нулю равен один из множителей:

х – s = 0 или х – k = 0

х = s или х = k

Так как при х = s или х = k в ноль обращается правая часть тождества, то также должна обращаться и левая часть. Получается, что числа s и k – это корни трехчлена х² + bх + с.

Убедимся в этом, раскрыв скобки в правой части тождества:

(х –s)(х –k) = х²–kx–sx + sk = х²– (k + s)х + sk

подставим это выражение в исходное равенство:

х² + bх + с = (х – s)(х – k) = х² – (k + s)х + sk

х² + bх + с = х² – (k + s)х + sk

Получается, произведение s и k дает свободный член, а их сумма в точности равна коэффициенту при х, взятому со знаком минус. Значит, по теореме Виета, они являются корнями уравнения!

Обозначим корни уравнения как х₁ и х₂. Если у трехчлена коэффициент а отличен от единицы, то эта формула (ее называют формулой разложения квадратного трехчлена на множители) примет несколько иной вид:

ах² + bx + c = а(х – х₁)(х – х₂)

То есть справедливо утверждение:

А теперь и докажем его.

Пусть есть уравнение ах² + bx + c = 0 с корнями х₁ и х₂. Поделим его на а:

х² + (b/a)х + с/а = 0

по теореме Виета можно записать:

х₁+ х₂ = – b/a

х₁•х₂ = с/а

Умножив первое тождество на (– а), а второе наа, получим

– а(х₁ + х₂) = b

ах₁•х₂ = с

Осталось подставить эти равенства в исходный многочлен:

ах² + bx + c = ах²– а(х₁ + х₂)х + ах₁•х₂= а(х²– хх₁–хх₂ + х₁•х₂) =

= а(х(х – х₁) – х₂(х – х₁)) = а(х – х₁)(х – х₂)

Для чего же мы доказывали эту теорему? С ее помощью можно выполнить разложение квадратного трехчлена на множители. Проиллюстрируем это на примерах.

Пример. Разложите полином

2х² + 12х – 14

на множители.

Решение. Для начала следует решить уравнение 2х² + 12х – 14 = 0:

D = 12²– 4•2•(– 14) = 144 + 112 = 256

Найдя х₁ и х₂, можем выполнить и разложение:

2х² + 12х – 14 = 2(х – 1)(х – (– 7)) = 2(х – 1)(х + 7)

Ответ: 2(х – 1)(х + 7)

Пример. Упростите выражение

Решение. На первый взгляд кажется, что сокращать нечего. Однако и в числителе, и в знаменателе находятся квадратные трехчлены. Разложим их на множители, решив соответствующие уравнения:

h²+ 2h– 15 = 0

D = 2² – 4•1•(– 15) = 4 + 60 = 64

Получаем, что

h²– 2h– 15 = (h+ 5)(h– 3)

Теперь раскладываем второй полином:

h²– 9h +18 = 0

D = (– 9)² – 4•1•18 = 81 – 72 = 9

Соответственно, можно записать:

h²– 9h +18 = (h– 3)(h– 6)

А теперь подставим в исходную дробь полученные выражения:

Отметим, что если у полинома второй степени нет корней, то и разложить его на множители не получится.

Дробно-рациональные уравнения

Периодически приходится сталкиваться с уравнениями, где переменные присутствуют в знаменателе какой-нибудь дроби. Их называют дробно-рациональными уравнениями. Обычно их можно свести к более простому виду, но при этом следует учитывать ту особенность, что корень уравнения не должен обращать знаменатель в ноль.

Пример. Найдите решение дробно-рационального уравнения

Решение. Для начала перенесем дробь из правой части в левую, а потом приведем дроби к общему знаменателю:

Умножим уравнение на величину (х – 2)(х + 3)

(х + 1)(х – 2) + 10х – 4(х + 3) = 0

х² – 2х + х – 2 + 10х – 4х – 12 = 0

х² + 5х – 14 = 0

D = 5²– 4•1•(– 14) = 25 + 56 = 81

Казалось бы, мы нашли два корня: 2 и (– 7). Однако в исходном уравнении в знаменателе стоит выражение (х – 2)(х – 3). При х = 2 оно обращается в нуль, то есть дробь потеряет смысл. Поэтому корень 2 следует отбросить, и остается лишь корень (– 7)

Ответ: – 7

Доброго времени суток, дорогие любители математики! Предлагаю Вам сегодня еще раз разобраться, как решать квадратные уравнения. Думаю, для многих читателей данный вопрос покажется простым, но сможете ли Вы навскидку назвать семь способов? А их, конечно, больше! Думаю, другие способы вспомните в комментариях.

Кстати, о комментариях! Там я часто вижу вопрос: «Почему Вы игнорируете формулы Виета?». Мне кажется, что на широкую аудиторию стоит транслировать наиболее простой способ — решение через дискриминант. Он понятный, его все помнят, а значит смогут разобраться в решении [и дочитают статью ;)].

Всем известно, что квадратное уравнение имеет вид:

Коэффициенты a, b и c здесь — это некоторые числа, а x — неизвестная. Для решения квадратного уравнения придумали общие формулы, понятные и простые.

Способ первый. Дискриминант.

Для решения квадратного уравнения через дискриминант его нужно вычислить:

А затем найти корни:

Все супер просто! Берем числа, получаем результат.

Пример:

Способ первый с половиной. Дискриминант, деленный на четыре.

Существует еще одна формула — для случая, когда второй коэффициент четный. Выведем ее:

Как видите, для четного коэффициента двойка будет всегда сокращаться, поэтому говорят о дискриминанте, деленном на четыре:

А корни будут находиться по такой формуле:

Проверим на нашем примере:

Корни сошлись, работает!

Способ второй. Выделение полного квадрата.

Формулы для дискриминанта очень занятные, но откуда они взялись?

Вернемся к началу:

Поделим все уравнение на a:

А дальше начнем шаманить. Мы хотим собрать полный квадрат по формуле сокращенного умножения:

В нашем уравнении на первом месте стоит x². На втором должно находиться удвоенное произведение. Создадим двойку искусственно, умножив и поделив на нее одномоментно:

Теперь у нас есть произведение двойки, x и некоторого числа. Для того чтобы получить формулу квадрата суммы прибавим это “некоторое число” в квадрате и сразу вычтем, дабы сумма не изменилась:

Все готово для формулы сокращенного умножения:

Перенесем все числа в правую часть:

Приведем к общему знаменателю:

Извлечем корень [считаем, что мы можем это сделать]:

Выразим икс и посмотрим, что же у нас получилось:

Да это же и есть формула из предыдущего способа!

Рассмотрим на примере:

Нам повезло и здесь двойка уже есть в наличии. Выделим полный квадрат:

Соберем полный квадрат:

Согласитесь, в числах выглядит гораздо проще и приятнее! Двигаемся дальше.

Способ третий. Разложение на множители.

Тут даже не буду пытаться сделать общие выкладки. Просто берем и раскладываем, как учили в восьмом классе.

Добавим «лишний» икс, получится:

Из первых двух слагаемых вынесем икс, из оставшихся — минус:

Вынесем за скобки общий множитель:

Произведение равно нулю, когда хотя бы один из множителей равен нулю:

Просто и надежно!

Способ четвертый. Формулы Виета.

Мы можем разложить квадратное уравнение на множители (как в прошлом способе). Получим такую картину:

Раскроем скобки:

Получили соответствие коэффициентам исходного уравнения:

Или, в привычном виде:

Удобнее всего пользоваться этими формулами, когда a = 1.

Приведем пример:

Здесь все еще можно воспользоваться дискриминантом, но вычисления будут некрасивые. Поэтому запишем формулы Виета:

Осталось подобрать корни. Для этого разложим 98 на множители:

Если первый способ разложения ничего не дает [ 2 + 49 = 51 ≠ 21]. То второй вариант дает нам корни:

Нахождение корней уравнения по формулам Виета — это простой и быстрый способ, всем рекомендую!

Способ пятый. Метод переброски.

Данный способ — эффективная модификация предыдущего способа для случая, когда a ≠ 1. Возьмем квадратное уравнение в общем виде:

И умножим все на a:

Введем замену:

Получим новое квадратное уравнение:

Таким образом мы как бы перебросили a к c. Теперь корни легко найдутся по формулам Виета. А для того, чтобы найти корни исходного уравнения, поделим найденные корни на a:

Приведем пример:

Произведем переброску:

О, а эти корни мы уже знаем:

Найдем иксы:

На мой взгляд, неплохо. Для участников олимпиад — обязательно к изучению.

Способ шестой. По свойствам коэффициентов.

Здесь все просто. Нужно запомнить, если:

То корни будут:

При этом второй корень мы нашли по формулам Виета.

И второе важное свойство, если:

То корни:

Список свойств не исчерпывающий, но другие свойства сильно сложнее, поэтому не будем их приводить.

В этот раздел также можно отнести старый добрый подбор корней.

Пример:

Здесь уже никакими дискриминантам и перебросками не поможешь. Но если заметить, что:

То сразу запишем:

Способ седьмой. Графический.

Есть два возможных варианта решения и оба имеют не очень хорошую точность. Во-первых, можно представить квадратное уравнение в виде:

И изобразить на координатной плоскости два графика: параболу и прямую.

Приведем пример:

Изобразим графики:

Получаем корни:

Конечно, график построенный автоматически позволяет достаточно точно углядеть корни. Но если у вас под рукой компьютер, то легче будет воспользоваться калькулятором и посчитать их. А вот изобразив график на бумаге определить корни будет сложно.

Разберем еще один графический вариант решения. На этот раз с помощью окружности.

Возьмем на оси абсцисс точки B ( x₁ ; 0 ) и C ( x₂ ; 0 ).

Посередине, между этими точками, будет находиться точка F, с координатами:

По формулам Виета:

На оси ординат возьмем точки A ( 0 ; 1 ) и D ( 0 ; c / a ). Посередине между ними будет находиться точка:

Точка S будет центром окружности:

Пусть O начало координат. Тогда OB · OC=OA · OD :

Таким образом для x₁ и x₂ выполняются формулы Виета.

Приведем пример:

Центр окружности будет иметь координаты:

Проведем окружность через точку A ( 0 ; 1 ) :

Получаем точки B ( 2 ; 0 ) и C ( 3 ; 0 ). А значит:

Как видите — способ рабочий, но опять же требует точности, которую на бумаге получить достаточно трудно.

Существует еще способ решения с помощью номограммы. Про него говорят “незаслуженно забытый”. Но на мой взгляд он забыт абсолютно заслуженно, так как преимуществ у него особых нет, а понять его сложнее, чем решение через дискриминант.

На практике я чаще всего использую формулы Виета и дискриминант. А какими способами пользуетесь Вы?

Спасибо за внимание и удачи!

Если вам понравилась статья, то ставьте лайк и подписывайтесь на канал. Математики будет много!