Как найти равенство отрезков

Отрезок

• Длина отрезка
• Равные отрезки
• Сравнение отрезков
• Середина отрезка

Отрезок — это часть прямой, ограниченная двумя точками, лежащими на этой прямой. Точки, определяющие границы отрезка, называются концами отрезка.

Отрезок обозначается двумя большими латинскими буквами, поставленными при его концах: отрезок  AB  или  BA.

Длина отрезка

Длина отрезка — это расстояние между концами отрезка. Любой отрезок имеет длину, бо́льшую нуля:

Измерение длины отрезка осуществляется путём сравнения данного отрезка с длиной единичного отрезка. Единичный отрезок — это отрезок, длина которого принимается за единицу. Следовательно:

длина отрезка – это положительное число, показывающее, сколько раз единичный отрезок и его части укладываются в данном отрезке.

Чаще всего используются единичные отрезки равные  1 мм,  1 см,  1 дм,  1 м  или  1 км. Измерить длину отрезка можно линейкой или любым другим прибором для измерения длины:

AB = 6 см.

Свойства длин отрезков:

• Основное свойство длины отрезка: если точка делит отрезок на два отрезка, длина всего отрезка равна сумме длин этих двух отрезков.

  
• Длины равных отрезков равны.
• Любой отрезок имеет определённую длину, большую нуля.

Равные отрезки

Равные отрезки — это отрезки, имеющие одинаковую длину. Если наложить равные отрезки друг на друга, то их концы совпадут.

Сравнение отрезков

Сравнить два отрезка — это значит определить, равны они, или один больше другого.

Сравнить два отрезка можно, отложив на прямой оба отрезка из одной точки в одну и туже сторону. Для этого можно воспользоваться циркулем.

Чтобы отложить на прямой отрезок равный данному, сначала помещают ножки циркуля так, чтобы острия их концов упирались в концы отрезка, а затем, не изменяя раствора циркуля, переносят его так, чтобы оба его конца находились на прямой.

При сравнении двух отрезков возможно получение одного из представленных результатов: отрезки будут равны, первый отрезок будет больше второго или первый отрезок будет меньше второго.

Если при наложении отрезков оба их конца совмещаются, значит отрезки равны.

При сравнении отрезков путём измерения их длин больше будет тот отрезок, у которого больше длина.

Если при измерении отрезков их длины равны, то и отрезки равны.

Середина отрезка

Середина отрезка — это точка, делящая отрезок на две равные части.

Отрезки и прямые, связанные с окружностью. Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках

Фигура	Рисунок	Определение и свойства
Окружность
Круг
Радиус
Хорда
Диаметр
Касательная
Секущая

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Радиус

Отрезок, соединяющий центр окружности с любой точкой окружности

Хорда

Отрезок, соединяющий две любые точки окружности

Диаметр

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Касательная

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Секущая

Прямая, пересекающая окружность в двух точках

Свойства хорд и дуг окружности

Фигура	Рисунок	Свойство
Диаметр, перпендикулярный к хорде		Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды	Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Равные хорды		Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
Хорды, равноудалённые от центра окружности	Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
Две хорды разной длины		Большая из двух хорд расположена ближе к центру окружности.
Равные дуги		У равных дуг равны и хорды.
Параллельные хорды		Дуги, заключённые между параллельными хордами, равны.

Диаметр, перпендикулярный к хорде

Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Равные хорды

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Хорды, равноудалённые от центра окружности

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Две хорды разной длины

Большая из двух хорд расположена ближе к центру окружности.

Равные дуги

У равных дуг равны и хорды.

Параллельные хорды

Дуги, заключённые между параллельными хордами, равны.

Теоремы о длинах хорд, касательных и секущих

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Фигура	Рисунок	Теорема
Пересекающиеся хорды
Касательные, проведённые к окружности из одной точки
Касательная и секущая, проведённые к окружности из одной точки
Секущие, проведённые из одной точки вне круга

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Пересекающиеся хорды

Касательные, проведённые к окружности из одной точки

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Пересекающиеся хорды

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Касательные, проведённые к окружности из одной точки

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Доказательства теорем о длинах хорд, касательных и секущих

Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).

Тогда справедливо равенство

Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).

Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство

Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).

Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство

Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).

Точка B – точка касания. В силу теоремы 2 справедливы равенства

откуда и вытекает требуемое утверждение.

Теорема о бабочке

Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.

Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:

Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим

Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим

Воспользовавшись теоремой 1, получим

Воспользовавшись равенствами (1) и (2), получим

Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство

откуда вытекает равенство

что и завершает доказательство теоремы о бабочке.

Равенство окружностей

Первый признак равенства окружностей

Формулировка первого признака равенства окружностей:

Если диаметр одной окружности равен диаметру другой окружности,
то такие окружности равны.

Доказательство первого признака равенства окружностей:

1. Рассмотрим окружность с диаметром BA и окружность с диаметром DC, в которых BA = DC. Докажем,
   что окружность с диаметром BA и окружность с диаметром DC равны.
2. BA = DC, значит окружность с диаметром BA можно наложить на окружность с диаметром DC так, что они совместятся:
   окружность с диаметром BA совместится с окружностью с диаметром DC.
3. Итак, окружность с диаметром BA и окружность с диаметром DC полностью совместятся, значит они равны — ч.т.д

Второй признак равенства окружностей

Формулировка второго признака равенства окружностей:

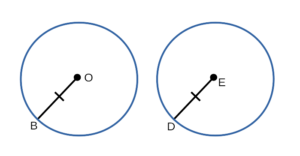
Если радиус одной окружности соответственно равен радиусу другой окружности, то такие окружности равны.

Доказательство второго признака равенства окружностей:

1. Рассмотрим окружность с радиусом BO и окружность с радиусом DE, в которых BO = DE. Докажем,
   что окружность с радиусом BO и окружность с радиусом DE равны.
2. BO = DE, значит окружность с радиусом BO можно наложить на окружность с радиусом DE так, что они совместятся:
   окружность с радиусом BO совместится с окружностью с радиусом DE.
3. Итак, окружность с радиусом BO и окружность с радиусом DE полностью совместятся, значит они равны — ч.т.д.

Третий признак равенства окружностей

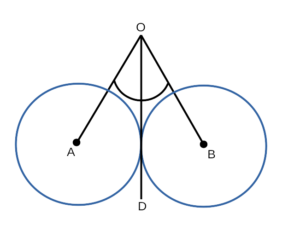
Формулировка третьего признака равенства окружностей:

Если луч делит угол между центрами двух окружностей на два равных угла, то такие окружности равны.

Доказательство третьего признака равенства окружностей:

1. Рассмотрим луч OD, окружность с центром в точке A и окружность с центром в точке В, отрезки OA и OB, в которых ∠AOD = ∠BOD. Докажем,что окружность с центром в точке A и окружность с центром в точке B равны.
   
2. ∠AOD = ∠BOD, значит отрезки OA и OB можно наложить друг на другу так, что они совместятся:
   отрезок OA совместится с отрезком OB.
   
3. Итак, окружность с центром в точке A и окружность с центром в точке B полностью совместятся, значит они равны — ч.т.д.

Равенство окружностей можно доказать с помощью трех признаков:

1. По диаметру.
2. По радиусу.
3. По лучу и углу.

Отрезки касательных

Рассмотрим, какими свойствами обладают отрезки касательных к окружности, проведенные из одной точки.

(Свойство касательных, проведенных из одной точки)

Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

AB=AC ∠BAO=∠CAO

Дано: окружность (O;R),

AB и AC — касательные к окружности (O;R),

B, C — точки касания.

Доказать: AB=AC, ∠BAO=∠CAO.

Следовательно, треугольники ABO и ACO — прямоугольные. У них

1) катеты OB=OC (как радиусы)

2) гипотенуза OA — общая сторона.

Из равенства треугольников следует равенство соответствующих сторон:

[spoiler title=”источники:”]

http://colibrus.ru/ravenstvo-okruzhnostey/

[/spoiler]

Приветствую всех читателей и подписчиков канала!

Задача.

Два квадрата имеют общую точку. Докажите, что отмеченные на рисунке отрезки АВ и СЕ равны.

Конечно, доказательство чего либо сложнее, чем просто решить и назвать ответ. Поэтому данная задача из программы ОГЭ может рассматриваться только как путь решения задачи. Ну вот, как бы вы, дорогой читатель, решали бы сами, или помогали решить задачу своим школьникам?

Что необходимо в первую очередь сделать для доказательства?

Конечно – сделать дополнительные построения. Какие? Или на что в данном чертеже нужно обратить внимание?

А представьте, ваш школьник на экзамене, волнуется, и нужно как можно быстрее сориентироваться, и выбрать нужный путь решения, причём не длинный и громоздкий.

В комментариях по желанию можно ответить: как можно доказать равенство отрезков АВ = СЕ, это очень не сложно, если найти эти отрезки в равных фигурах. Можно не смотреть видео с решением, а можно и посмотреть в качестве подсказки.

Поэтому даю подсказку и само решение в видео.

Спасибо за просмотр статьи и видео!

Ответы и вопросы пишите в комментариях.

Подписывайтесь на канал Тесты_математика!

#задачи на логику , #задания на логику , #математика ,

Тема урока: «Отрезок. Длина отрезка.
Равенство  отрезков»

5 класс

·        
Цель урока: Сформировать понятие отрезка,  рассмотреть,
что такое  длина отрезка, равенство отрезков, взаимное расположение отрезков.

Задачи
урока:

1.      Добиться
усвоения учащимися содержания новых понятий  урока,

формировать исследовательские
навыки, учить планировать свою деятельность, развивать критическое и логическое
мышление, творчески мыслить, обобщать полученные знания.

2.      Формировать
УУД:

Познавательные
УУД:

·        
Уметь ориентироваться в своей системе
знаний: отличать новое от уже известного с помощью учителя; добывать новые
знания: находить ответы на вопросы, используя свой жизненный опыт и информацию,
полученную на уроке;

·        
создание проблемной ситуации, побуждающей
учащихся к поиску новых решений;

·        
уметь сравнивать и измерять длины отрезков
при помощи мерок;

·        
формировать представление о различных
случаях взаимного расположения двух отрезков.

Коммуникативные
УУД:

·        
Уметь слушать и понимать других;

·        
строить речевые высказывания в соответствии
с поставленными задачами;

·        
оформлять свои мысли в устной форме;

·        
уметь работать в группе.

Личностные
результаты:

·        
Уметь высказывать своё мнение, выражать
свои эмоции;

·        
оценивать поступки в соответствии с
определённой ситуацией;

·        
формируем мотивацию к обучению
целенаправленной познавательной деятельности.

Регулятивные
УУД:

·        
Оценивать правильность выполнения
действия;

·        
вносить необходимые коррективы в действие
после его завершения на основе его оценки и учёта характера сделанных ошибок;

·        
высказывать своё предположение,
осуществлять познавательную и личностную рефлексию.

Тип
урока: урок объяснения нового материала и первичного закрепления знаний

Методы
обучения: фронтальная беседа, индивидуальная работа.

Оборудования
урока: презентация Microsoft Power Point,
две одинаковые верёвки по 30 см, две полоски бумаги 2 см и 3 см, электронная
доска.

Структура
урока:

1.      Организационный
момент. Психологический настрой учащихся.

·        
Посмотрите друг на друга, улыбнитесь,
пожелайте успешной работы себе, соседу, всему классу.

2.      Мотивационное
начало урока. На доске слова «Я думаю, что никогда до настоящего времени мы не
жили в такой геометрический период. Всё вокруг – геометрия».  Лэ Корбюзье.
Учитель: »Как вы думаете, эти слова подходят для нас?»

Учитель: «Что такое
геометрия? Едем Родосский (IV
век  до н.э.) так объясняет происхождение  термина «геометрия»: «Геометрия была
открыта египтянами и возникла при измерении Земли. Это измерение было им
необходимо вследствие разлития реки Нила, постоянно смывавшего границы
участков. В переводе с греческого слово «геометрия» означает «землемерие»
(«гео» – по-гречески земля, а «метрео» – мерить) » Слайд№1

слайд№2

Основные понятия
геометрии: отрезок, прямая, плоскость. Сегодня мы остановимся более подробно на
понятии отрезок. Запишем в тетради число и тему урока «Отрезок. Длина отрезка.
Равенство  отрезков».

3.     
Изучение нового материала.

1)      Отметьте
в тетради точки. Обозначьте их. Обозначить – это дать имена. Имя точки – большая
латинская буква.

2)      С
помощью линейки проводим линии, соединяющие эти точки. Линия в переводе с
латинского  – льняная нить. Слайд №3 и слайд №4

Учитель: «Как вы думаете,
как эта фигура называется? Ответ (АВ – отрезок, запись на доске и в тетрадях).
Как называются точки А и В?(концы отрезка  А и В)

Часть прямой, заключённой
между точками называется отрезком».

3)      Соединим
точки А и В другими линиями. Будут ли эти линии отрезком? Ответ(нет. отрезок
самый кратчайший путь)

4)      Нарисуйте
на листке 6 отрезков. А теперь  с помощью минимального количества линий
соедините их, так чтобы получилась картина.

5)      Где
среди окружающих нас предметов в классе мы видим отрезки?

6)      Как
сравнить два отрезка? (ответы учащихся)

7)      Как
сравнить два отрезка без линейки?

Решение:
Наложить отрезок АВ на отрезок СD
так ,чтобы начало одного совпало с началом другого

a)      если
отрезок АВ составляет часть отрезка CD,
то он меньше отрезка CD(AB<CD)

b)      если
отрезок CD
составляет часть отрезка AB,то он меньше
отрезка AB(AB>CD)

c)      если
отмеченный конец отрезка AB совпадает с
точкой D,
то отрезки АВ и CD равны (АВ=CD).Два
отрезка на плоскости называются равными, если существует перемещение, при
котором копия одного отрезка совмещается с другим отрезком.

Учитель: Что такое длина
отрезка? Что же нам нужно, чтобы найти расстояние? (ответы учащихся) Такие
единицы измерения принято называть единичными отрезками, тогда измерить –
значит сравнить с эталоном. Длина – это некоторое число, которое показывает,
сколько раз единица измерения укладывается в измеряемом отрезке.

4.      Практическая
работа:

Возьмите верёвку и в
качестве единицы измерения – полоску бумаги. И начинайте откладывать по верёвке
эти полоски. Сколько получилось полосок? Возьмите вторую верёвку и проделайте
ту же процедуру. Сколько получилось полосок? Сравните верёвки (они одинаковые).
А почему разные измерения? (разные единицы измерения). От чего зависит длина
отрезка? (от единицы измерения). Какой можно сделать вывод? (чем больше единица
измерения, то её укладывается в измеряемом отрезке меньше раз  и наоборот).
Можно ли сравнить отрезки, если мерки разные? (нет).

Старинные меры длины.
Какие старинные меры длины вы знаете или слышали названия дома, в сказках?
(слайд №5),слайд№6)слайд №7слайд№8

5.      Давайте решим старинную
задачу из сборника «Арифметика» Магницкого. «Идёт один человек в другой город и
проходит ежедневно 40 вёрст, а 2-ой человек идет на встречу к нему из другого
города и проходит в день 30 вёрст. Расстояние между городами 700 вёрст. Через
сколько дней путники встретятся? (Через 10 дней).

Ещё существует такая мера
длины – шаг. Давайте измерим длину нашего класса. Что вы заметили? (Разные
результаты). Удобно пользоваться старинными мерами длины? (нет). Значит, чтобы измерить
длину отрезка, надо выбрать единицу измерения одинаковую для всех.

Метр – основная мера в
системе мер, принятой практически во всех странах. Она так и называется –
метрическая система мер.

 Учитель: Какие единицы
длины используют для точного измерения кроме метра? (миллиметр, сантиметр,
дециметр).

1 метр = … см

1км = … м

Во сколько раз 1 м больше
1 см ?

1м = … дм

1км = … м

Во сколько раз 1 м больше
1 дм?

Рассмотрим (слайд № ) на
нём изображён отрезок АВ и точки О, D
и С. Как располагаются точки по отношению к отрезку? Введём понятия: «… лежит
на отрезке» , «… принадлежит отрезку» , «не принадлежит отрезку» и обозначения
: Введём понятия: «… лежит на отрезке» , «… принадлежит отрезку» , «не
принадлежит отрезку» и обозначения : Є(принадлежит), (не принадлежит) слайд№9

6.     
Физкультминутка

1.     
Быстро поморгать, закрыть глаза и посидеть
спокойно, медленно считая до 5. Повторять 4-5 раз.

2.     
Крепко зажмурить глаза (считать до 3),
открыть их и посмотреть вдаль (считая до 5). Повторить 4-5 раз.

3.     
В среднем темпе проделать 3-4 круговых
движения глазами в правую сторону, столько же в левую сторону. Расслабив
глазные мышцы посмотреть вдаль на счёт 4-6. Повторить 1-2 раза.

Вопросы для актуализации
внимания:

Учитель:

Давайте поговорим о 
взаимном  расположение 2-ух отрезков. Что вы можете мне об этом сказать? ответы
учащихся: (отрезки могут пересекаться или не пересекаться, иметь общую точку,
отрезок может лежать на другом отрезке). Возьмите свои верёвки и покажите
различные взаимные расположения двух отрезков.

 Давайте посмотрим,
правильно ли вы рассуждали, воспользовавшись слайдом (слайд № 11) Закрепление
по упражнениям на странице учебника 76.

Итог урока: Что нового мы
узнали сегодня на уроке? Где в жизни можно применить знания, полученные на
уроке?